Experimental study on creep wetting of silty clay

1. Introduction

Silty clay is widely distributed all over the world, also distributed in Chongqing. There are many riverside roads in Chongqing area, and the bearing layer under the subgrade is silty clay. The riverside roads subgrade along the river was wetted by the water all years round, soil particles were rearranged and adjusted under the water, resulting in additional deformation and additional settlement of subgrade, thus causing deformation and cracking of pavement and even instability and failure of embankment slopes along the river, the long-term stability of the road’s subgrade was affected. When the author conducted the water wetting test on the silty clay as the bearing layer under the subgrade [1], [2] found that the water wetting deformation test lasted for a long time, reaching 100 hours or even longer, so the creep deformation with time cannot be ignored.

Many scholars has studied the subgrade soil, such as coastal soft soil subgrade [3-5], soft clay [6]and structural clay [7] in different areas. The above researches have promoted the study of creep characteristics of different soil mass, but most of them consider the creep test of soil mass under a single stress state [4]. In fact, in view of the fact that the creep phenomenon of soil is mostly viscoelastic and plastic, and the stress state has a significant impact on the creep characteristics of soil, it is of great significance to study the creep characteristics of silty clay at different stress levels.

This paper takes the silty clay widely distributed in Chongqing area as the research object. Through triaxial drained shear creep tests under different stress levels, it focuses on demonstrating the creep characteristics of silty clay after wetting in water, and discusses its corresponding suitable model, so as to understand its deformation mechanism in depth.

2. Silty clay sample properties and test method

3. Analysis of creep test results

3.1. Creep stress-strain curve

The creep stress-strain curve of the creep test is shown in Fig. 1, the curve is processed by Chen’s method [8]. Under the same confining pressure, the silty clay creep deformation amplitude at low stress level is small, the stress-strain curve is almost a straight line. At higher stress level, the strain gradually increases with time, and the creep deformation also increases.

At the same stress level $D$, the creep deformation and rate under high confining pressure are larger than those under lower. When the stress level $D=$ 0.75, the creep rate far exceeds other stress levels.

Fig. 1Creep stress-strain curves under different confining pressures

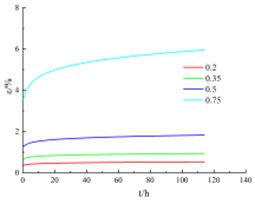
a) Confining pressure = 100 kPa

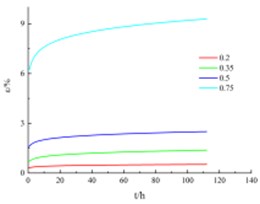
b) Confining pressure = 200 kPa

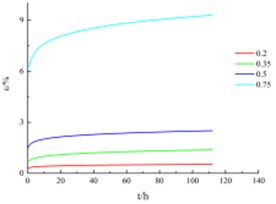
b) Confining pressure = 300 kPa

3.2. Creep isochronous stress-strain curve

The shape of stress-strain isochronous curves at different times is shown in Fig. 2, which indicates that silty clay has obvious creep characteristics. When time $t=$ 0, the s stress-strain isochronous curve is approximately a straight line, so it can be considered that the initial deformation is elastic deformation.

When time $t>$0, with the extension of creep time, the isochronous stress-strain curve gradually deviates from the straight line and bends toward to the strain axis, and the longer the creep time, the higher the degree of deviation of the isochronous curve from the straight line, and the more obvious the bending toward to the direction of the strain axis.

The test results show that, from the beginning of loading, the stress-strain isochrone curve shows obvious nonlinear characteristics, and its nonlinear degree is related to creep time and stress level. The higher the stress level $D$ is, the more obvious the axial bending toward the strain axis, the longer the creep time, the higher the nonlinear extent.

Fig. 2Stress-strain isochronous curves

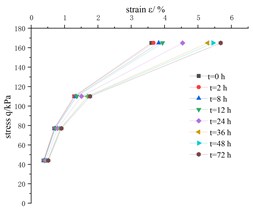
a) Confining pressure = 100 kPa

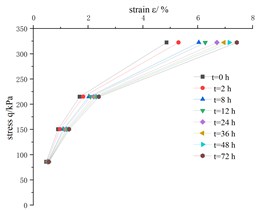
b) Confining pressure = 200 kPa

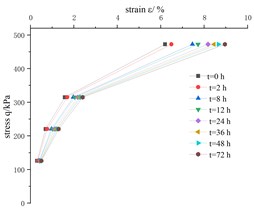
c) Confining pressure = 300 kPa

4. Applicable model of creep stress-strain curve

At present, there are three ways to describe the creep characteristics of rock and soil: theoretical model based on model theory, empirical model based on test results and micro model derived from micro rheology. The former two approaches are most widely used.

A. Singh and J.K. Mittechell [9] proposed the classical Singh-Mitchell creep model on the basis of summarizing the single-stage constant stress loading, drained and undrained triaxial compression test data, and proposed that the stress-strain relationship can be expressed by an exponential relationship and the strain time relationship can be expressed by a power function, which is a three parameters model used to describe the deviator stress level within 20 %-80 %, and can well reflect the creep characteristics of soil. The equation of Singh Mitchell creep model is as follows:

When ${\epsilon }_0=0$, the Eq. (1) can be expressed as:

where, $B=A{t}_1/1-m$, $\beta =\alpha$, $\lambda =1-m$, $m$ – absolute value of the slope of the straight line in the relation curve of $\mathrm{l}\mathrm{o}\mathrm{g}\dot{\epsilon }~\mathrm{l}\mathrm{o}\mathrm{g}t$.

This is the mathematical expression of the Singh-Mitchell model. When expressed by strain, there are three parameters $B$, $\beta$, $\lambda$, the model parameters can be determined according to the test results. Creep test can be controlled by drainage conditions, so the Singh-Mitchell model can describe both drainage conditions and undrained conditions [8].

When $t=t_1$, the Eq. (2) can be expressed as exponential stress-strain relation:

Take the logarithm on both sides:

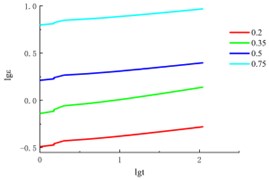
Fig. 3The logε~logt curve

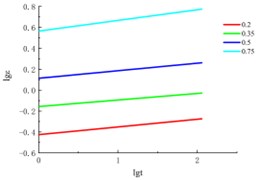
a) Confining pressure = 100 kPa

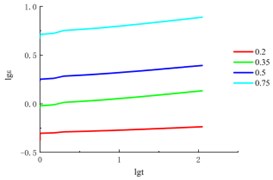
b) Confining pressure = 200 kPa

b) Confining pressure = 300 kPa

Based on the above formulas and creep test results, $B$ can be directly obtained from the relationship curve of soil samples at different times, $\lambda$ is the slope of the model parameter straight line is related to the deviator stress $D$, which can be taken as the average value when the difference is not large, calculation results see in Table 2. Collating the creep data, draw the$\mathrm{}\mathrm{l}\mathrm{o}\mathrm{g}\epsilon ~\mathrm{l}\mathrm{o}\mathrm{g}t$ curve, as shown in the Fig. 3.

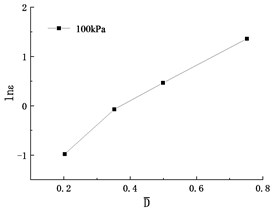
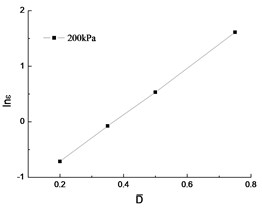
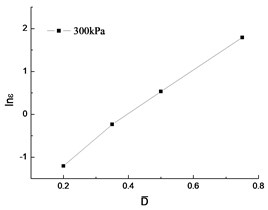
Fig. 4The lnε~D- curve

a) Confining pressure = 100 kPa

b) Confining pressure = 200 kPa

b) Confining pressure = 300 kPa

Parameter $B$, $\beta$ can be directly obtained from the relationship curve of $\mathrm{l}\mathrm{n}\epsilon ~\stackrel{-}{D}$ in Fig. 4, the linear relationship is relatively good. Table 3 shows the calculation results.

The Singh Mitchell model equation of the creep stress-strain curve of silty clay is:

This model can well describe the creep stress-strain curve of silty clay. The larger the stress level, the worse the data consistency. If the stress level exceeds 0.8, there will be a large deviation, the Singh-Mitchell model is not suitable for describing the creep curve.

5. Conclusions

In this paper, the triaxial creep wetting test was successfully carried out, and the creep deformation characteristics were revealed.

1) The silty clay of road subgrade along the Jialing River in Chongqing has obvious creep characteristics.

2) Use the graded loading method, obtained sufficient creep test data, which provides a basis for testing the accuracy of the creep model.

3) Introduced the Singh-Mitchell model to describe the creep stress-strain curve, calculated the parameters $\left(\lambda ,\beta ,B\right)$ of silty clay.

In the actual project, the structure of soil mass must be fully obtained. Necessary supporting structures must be added to control the creep deformation. Next study will focus the creep deformation of silty clay under cyclic loading for a longer time.