Application of PID controller in chemical process system using COMSOL

1. Introduction

The concept of process industry describes key raw material industries such as petroleum, chemical engineering, steel, iron, and building materials. These industries are significant for developing the national economy and ensuring sustainable growth of production power worldwide. With equipment, production techniques, and automation systems in the process industry, more efficient and quality products have begun to be produced [1-3]. The manufacturing sector must recently show a tendency to merge with information technology. Thus, the way for intelligent and optimal production systems will be opened [4, 5].

The chemical process industry is a self-renewing entity that needs to be constantly improved to adapt to current technologies. The chemical industry provides an opportunity to develop products as products based on chemicals with higher added value. Process safety is vital in chemical industry operations, especially when handling hazardous substances for humans, the environment, and infrastructure [6, 7]. The maintenance of safety compliance while ensuring product consistency, high productivity, and cost-effectiveness is chemical manufacturers' primary challenge today. In such harsh conditions, controlling the process with a controller is crucial. Different control algorithms have been applied in many industrial applications from the past to the present. These are statistical process control, model predictive control, adaptive control, single loop digital control, feedforward artificial neural network, and PID control [8-10].

Proportional-Integral-Derivative (PID) control algorithms have been widely used in many industrial applications for the last sixty years. Jamil et al. discussed the improvement of fractional proportional integral derivative controllers, temperature control in ambulances, induction heating systems, control of bioreactors, and temperature control systems [11]. Also, a comparison of conventional and FOPID controllers is highlighted to show the improvement in production, quality, and accuracy that can be achieved using such controllers. Feng et al. discussed the weighted sensitivity design of multivariate proportional-integral-derivative (PID) controllers for multiple-input multiple-output (MIMO) processes [12]. Three application examples are given to demonstrate the effectiveness and good performance of the method for practical industrial processes. Dubey et al. have published a review article on the role of PID control techniques in the process control system [13]. This article aims to focus on the journalistic evaluation of the PID controller in the process control system era. The most important reason for this review article is to present it comprehensively to a group of people who know the control of PID controllers in industrial control systems. The methods discussed in the article are classified from traditional to artificial intelligence (AI) used for PID controllers. Bhookya et al. Carried out a study on implementing the PID controller for the liquid level system and integrating the IoT application using modified gray worm optimization (mGWO) [14]. This research proposes IoT-based real-time liquid level monitoring and control in a single tank system. A PID controller with parameter sets using a new mGWO algorithm manages the fluid level. Today, the PID method is used in more than 90 % of applied control systems, from consumer electronics to industrial processes such as chemicals [15, 16]. The PID controller helps to reach the desired system output to the desired level in a short time with minimum error. Depending on the application area, this system output sometimes includes process parameters such as temperature, humidity, and flow and sometimes includes industrial processes such as speed and location.

PID controller is one of the most preferred control methods in the industry due to its reasonable cost and advantages. One of the most significant advantages of this controller is that it gives good responses in nonlinear systems [17, 18]. Many nonlinear process controls use well-known and industrially proven PID controllers. The difficult part of process controller design is figuring out how much of a corrective effect the controller will have on the process in each case. For this, the coefficients of the PID controller should be determined at the optimum level.

Controlling any system is very important in the chemical process industry. For this, selecting a controller compatible with the system is necessary. PID controller, one of the most preferred methods in this process, is a critical way to achieve this. The most important problem in the implementation of this controller is the optimization of the PID parameters. This work demonstrates the application of the PID control algorithm in COMSOL to simulate any chemical process control system. This application can be integrated into a system where the concentration in the combustion chamber is adjusted. As a result of mixing the two gases in the combustion chamber, the concentration is measured, and ignition takes place. The flow rate of the gases can be changed with the PID controller to obtain the desired concentration.

2. Material and method

2.1. Model definition

The model geometry and mesh structure developed in the COMSOL program are shown in Fig. 1. While developing this model, the chemical process system was taken as a reference. Here, a structure with two inputs and one output has been created. A gas stream with high oxygen content enters the reactor at a speed of 0.02 m/s from Input-2, while another gas with a low oxygen level enters from Input-1. Input-1 is used as the controlled input. After mixing the two gases, the oxygen concentration is determined at a measuring point. To obtain the desired concentration value, the inlet velocity of the gas with less concentration is changed by the Proportional Integral Derivative (PID) control algorithm. The density and viscosity of the liquid material used for modeling and analysis must be specified. For this, the material definition was made in the COMSOL program. In this study, the density and viscosity values for the liquid were entered as 1.1 kg/m³ and 3E-5 Pa·s, respectively.

For the analysis of the developed model, some definitions must be made in COMSOL. Before the analysis process, it is assumed that the flow of gases is incompressible and there are no reactions. The laminar flow interface is used to define the fluid flow here. Also, a diluted species transport interface was used to maintain the mass balance in the flow of gases. The following laminar flow equations are used in the analysis process within the determined limits:

1

$\rho \frac{\partial u}{\partial t}-\nabla \bullet \left[\eta \left(\nabla u+{\left(\nabla u\right)}^T\right)\right]+\rho u\bullet \nabla u+\nabla p=0,$
$\nabla u=0,$
$\frac{\partial c}{\partial t}+\nabla \bullet \left(-D\nabla c\right)=-u\nabla c.$

A flow less boundary condition defines all walls. In this equation, the concentrations of the two inputs in the process need to be known to formulate the boundary conditions. It is also assumed that the reagent transport occurring at the outlet is mainly driven by convection. In this study, the boundary conditions for mass balance and fluid flow are given in Table 1.

Fig. 1Process control system developed in the COMSOL program

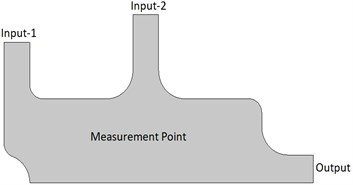
a) Model geometry

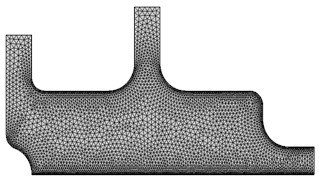
b) Mesh structure

Table 1Boundary conditions for mass balance and fluid flow

Mass balance	Boundary	Constraint
	Input-1 Input-2 Output Walls	$c=c_{input\_1}$ $c=c_{input\_2}$ $n\bullet \left(-D\nabla c\right)$ $N\bullet n=0$
Fluid flow	Boundary	Constraint
	Input-1 Input-2 Output Walls = 0	$u=\left(u_{in},0\right)$ $u=\left(0,-v_{input\_2}\right)$ $p_0=0$ $u=0$

One of the symbols related to the mass balance parameter, $c$, represents the concentration of the liquids. $c_{input\_1}$ and $c_{input\_2}$ define the concentrations (mol/m³) of the controlled and upstream inputs, respectively. Finally, $D$ is the applied diffusivity (m²/s); $N$ is the molar flux (mol/(m².s)). Of the parameters related to the fluid flow, $u$ is the velocity vector, $v_{input\_2}$ is the liquid inlet velocity in the upper section, and $u_{in}$ denotes the PID-controlled velocity. The outlet pressure was fixed at 0 during the analyses. A smooth transition to the laminar velocity profile is achieved by defining all wall numbers.

The standard controller algorithm used to calculate the PID-controlled speed parameter is as in the equation below. In addition, PID parameters $\left(c_{set},k_p,k_I,k_d\right)$ used for control were entered as 0.7 mol/m³, –0.5 m⁴/(mol.s), –1 m⁴/(mol.s²) and –1E-3 m⁴/mol, respectively:

2

$u_{in}\left(t\right)=k_p\left(c_{set}-c\left(t\right)\right)+k_I{\int }_0^t\left(c_{set}-c\left(\tau \right)\right)d\tau -k_d\frac{\partial }{\partial t}c\left(t\right).$

The negative values of the PID control coefficients indicate that $c_{set}$ is lower than the concentration in Input-2 and the gas flow in the controlled input, Input-1, is to reduce the concentration. In chemical process-controlled systems, the derivative effect in PID is usually taken as 0. This is because the $k_d$ parameter is difficult to determine and increases fluctuations in the system response.

3. Results and discussion

After the modeling phase of the proposed chemical process system, the analysis process was carried out. The analyses cover the oxygen’s pressure distribution, concentration amount, and velocity distribution in the process. In addition, the concentration and velocity of the fluid were kept at a certain level with the PID control algorithm. The parameters applied to the model during the analysis are given in Table 2.

The oxygen concentration and velocity flow lines resulting from the fluids applied simultaneously to the model from the two entry points are shown in Fig. 2. These data were taken during periods where the flow time was 0.05 s and 2 s. While the fluid with high oxygen level is sent from Input-2 input, low-level fluid is sent from Input-1. The concentration distributions resulting from mixing the two fluids are given in Fig. 2(a). The concentration level stabilizes as the mixture of liquids approaches the exit point. The results show that the measured concentration highly depends on the flow field. The velocity distribution during the concentration is given in Fig. 2(b). As expected, the velocity levels increased as the two fluids applied at low velocity approached the exit point. Initially, when the inlet velocity of the left inlet flow is too low, the sensor is completely exposed to the flow of high concentration. An inverse relationship occurs as the left inlet velocity increases.

Fig. 2Oxygen concentration and velocity streamlines

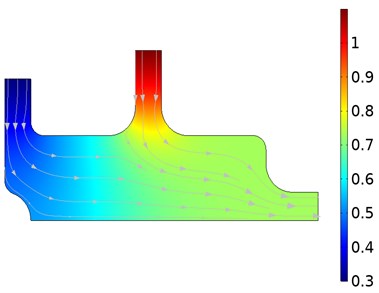
a) Oxygen concentration distribution

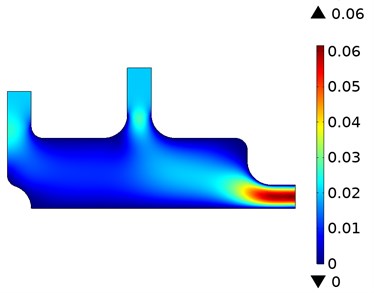
b) Velocity distribution of fluids

The input velocity and concentration at the measurement point calculated as a function of time for different proportional gain ($k_p$) values are given in Fig. 3. The blue, green, and red lines on the figure represent different $k_p$ parameters, respectively. These parameter values correspond to –0.1 m⁴/(mol·s), –0.5 m⁴/(mol·s) and –1 m⁴/(mol·s) $k_p$, respectively.

Fig. 3PID-controlled inlet velocity and concentration in the measurement point as a function of time

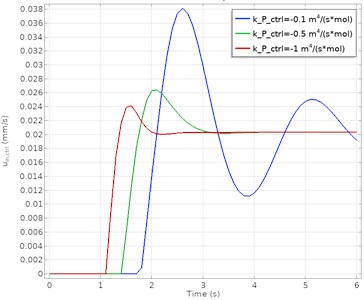
a) PID controlled velocity response

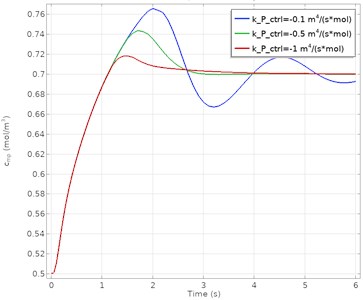
b) PID controlled concentration response

The results show that the PID control algorithm is successful at high proportional gain values. At lower $k_p$ values, the system gave an oscillatory response. More oscillations appear at the lower gain parameter before stabilization is achieved. As a result, it is seen that a more stable and steady-state error-free process control is obtained at higher $k_p$ parameters. It has been determined that the best process response in both concentration and velocity data is achieved when $k_p=$ –1 m⁴/(mol·s). The comparison of the PID controller in terms of performance criteria is presented in Table 3.

4. Conclusions

To realize a healthy and efficient production process in the chemical process industry, all parameters must be kept under control. It is necessary to choose the optimum algorithm compatible with the system for this control. In this study, the PID control algorithm, frequently used in industrial applications, has been implemented in the COMSOL program. The concentration level and velocity flow of the model consisting of two inputs and one output were controlled. The flow rate of the fluids can be changed with the PID controller to achieve the desired concentration. As a result of the simulation with different PID coefficients, the best response was obtained when the high proportional gain coefficient was applied. High overshoot and steady-state error occurred at low gain values in the system response. It has been determined that the best process response in both concentration and velocity data is achieved when $k_p$ = –1 m⁴/(mol·s). This application can be integrated into a system where the concentration in the combustion chamber is adjusted. As a result of mixing the two gases in the combustion chamber, the concentration is measured, and ignition takes place. The flow rate of the gases can be changed with the PID controller to obtain the desired concentration.