Research and design of program complexity measurement technology based on OINK framework

1. Introduction

Complexity measurement analysis assesses the complexity of a program’s source code in terms of its structure, length, size, etc. so in a sense complexity measurement analysis also belongs to the category of program understanding, and is a key part of the software static analysis technology. Complexity analysis can reflect the error rate in the process of software development and reduce the possibility of software failure, so as to improve the quality and maintainability of software [1]. The research on program complexity analysis technology should eventually be implemented in the research on one or more complexity measurement algorithms, so the most concerned problem is the data measurement element problem [2]. Based on program understanding, these metrics come directly or indirectly from the abstract syntax tree. Therefore, how to ensure that the data information on the nodes of the abstract syntax tree is used as measure element of software complexity after correct and reasonable analysis and statistics is the problem we need to solve.

Program complexity measurement analysis technology belongs to the category of code static analysis, and the static analysis technology of foreign source code has reached the third generation [3]. For example, Klocwork Insight, a source code analysis tool belonging to Klocwork, is the first tool that allows developers to control the entire analysis process and benefit from the accuracy of centralized analysis. Klocwork Insight allows developers to perform local analysis in the development environment they are familiar with, and can also achieve the consistency and analysis accuracy obtained by doing the same analysis steps in the integration verification phase. The tool for software complexity measurement mainly includes McCabe complexity, Halstead program measurement, number of code lines, number of inheritance, number of loops and other basic metrics [4-6]. At present, China’s research on this technology is still in the initial development stage, the scale is relatively small, and few scientific and technological personnel participate in the research. From the perspective of technical research, some technologies are still in the second stage of source code analysis, namely the centralized analysis stage. However, there are also some excellent tools of China, such as Safe Pro C/C++ developed by the Beihang University Software Engineering Institute. It provides user working environment with multi-selection window and single-driven; and supports fast association analysis of several test information. From the current situation of domestic and foreign research, the software complexity analysis technology of programs has not yet reached the mature stage [7]. The research of software complexity analysis technology also needs to be continuously improved. However, these traditional measurement algorithms can also reflect the complexity of software development to a certain extent. The key is how to use these measurement methods to evaluate the complexity of software reasonably and stably, reduce the possibility of software failure and improve the maintainability of software, so as to achieve the purpose of enhancing software quality.

Based on the above point of view, according to the current software testing requirements, this paper proposes a program complexity measurement technology based on OINK static analysis framework by using the principles of semantic analysis, syntax analysis, abstract syntax tree, local analysis and global analysis in static analysis. This technology can effectively combine the complexity measurement parameters and static analysis tools, and will be applied to the program understanding platform, so that the program complexity analysis results are more accurate and reliable. At the end of the article, the correctness of this technology is proved by designing the test environment and process, and verifying the results by various measurement methods.

Our technology will be developed based on the open source framework, open up solutions, and have extremely reliable results, which is a very powerful outstanding advantage. Through mass discussion and supervision, it will produce stronger and more reliable results, benefit more enterprises and communities, and promote the vigorous development of process complexity measurement technology.

2. Program complexity research

Complexity is relative to simplicity, which refers to the characteristics of single, certainty, fixation, invariance; the complexity refers to the characteristics of diversity, uncertainty, randomness and variability [8]. Program complexity is a fundamental feature of program, but there is no accepted precise definition. Most researchers believe that program complexity is the difficulty of analyzing, designing, testing, maintaining and modifying software, and the difficulty will increase day by day; and some researchers believe that program complexity is mainly structural complexity and algorithmic complexity, which gradually occur in the software life process, especially in the design and coding phase [9]. Therefore, in order to study the program complexity, the analysis of the process of program structural complexity is the first step, and on this basis, it determines what kind of measurement method is used to quantify the complexity:

The process of analyzing the generation of program complexity is to generate the mapping relationship $M$, from software code $C$ and the relationship between codes $R$, to the complexity measurement results $N$, and the numerical relationship between measurement results $P$.

Take structured program $SP$ as an example:

$S$ includes basic statements (empty statements, assignment statements, procedure call statements), sequence control statements $Seq$, structure control statements $Sel$, and loop control statements $Rep$.

The measurement of program complexity is to give an expression to each program, and use this expression to describe various characteristics of program complexity. If $S_1\in SP$, $S_2\in SP$:

where $\times$represents the multiplication of expressions.

where $+$represents the addition of expressions.

where $r≔r^c$represents substituting $r$ with $r^c$ in the expressions.

2.1. Performance behavior of procedural complexity

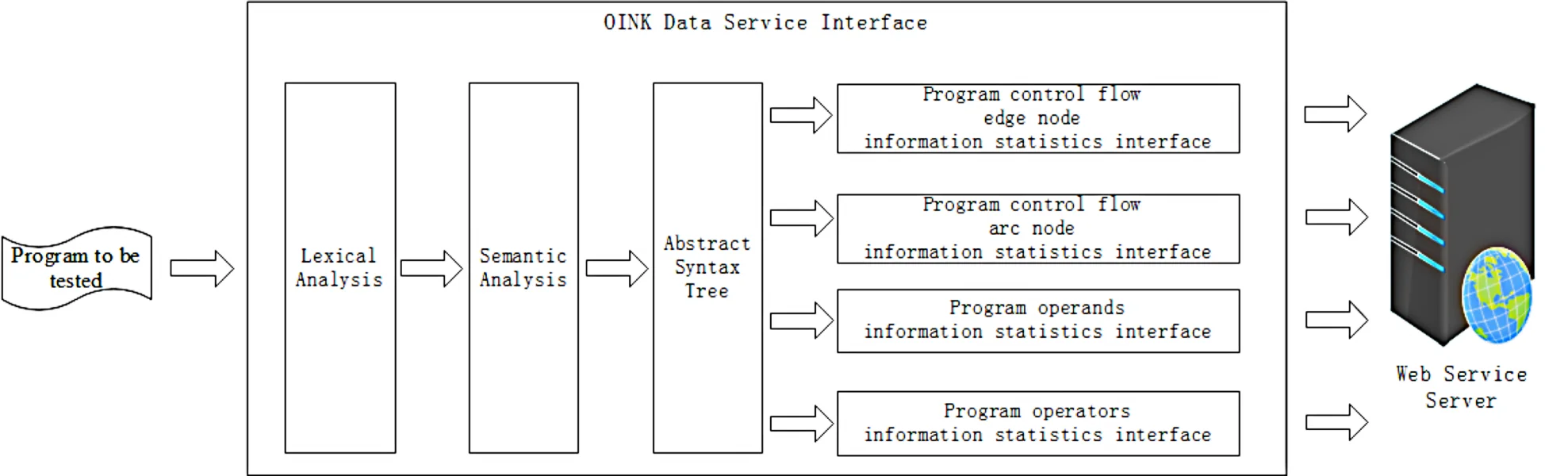
The main reasons for program complexity are: the complexity of operating environment, software requirements, data model, design process, software project management, software architecture, project testing and non-formal methods [10]. These reasons are ultimately manifested in the complexity of program code data structure and control structure, where both control flow and data flow generation are derived from abstract syntax trees in program understanding techniques. Abstract syntax tree is generated by the input source program through lexical analysis, syntax analysis and semantic analysis, and transformed and filtered through the basis of the parse tree. Fig. 1 shows the process of program complexity of the static analysis.

Fig. 1Program static analysis process

3. Analysis and design of OINK frame structure

OINK is an open source program understanding tool, which can complete lexical analysis, syntax analysis, abstract syntax tree and program flow diagram to realize software complexity analysis. Its core function is program understanding. OINK can perform many static analysis methods of C and C++ programs, mainly for data stream analysis. In the program understanding function, it includes analyzing and processing the data flow at the expression level and type level of the source program, and the control flow at the statement level (which is realized by the relevant functions of Elsa). It can also realize the output of the analysis results such as the data flow graph of program, the control flow graph, and the class inheritance relationship graph (C++).

3.2. Design of OINK data service interface

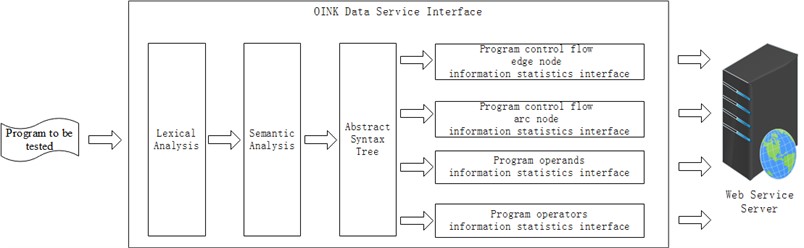
Through the previous analysis, it can be concluded that OINK can complete semantic analysis, lexical analysis and abstract syntax tree construction in the process of program understanding. On this basis, the OINK data service interface is designed, which can provide data measurement element for program complexity measurement technology. Fig. 3 shows the OINK data service interface. In Fig. 3, the information statistical interface of edge nodes and arc nodes provides measurement data onto program control structure (i.e., McCabe standard); the information statistical interface of program operands and operators provides measurement data for the physical structure of the program (i.e., Halstead standard). These service interfaces are all deployed on the server in the form of Web Service [14].

Fig. 2OINK source code file structure

Fig. 3Design of OINK data service interface

The operations performed by the data service interface can be defined as the following formula:

19

$R=F\left(C\right).$

$F$ represents the operation done by the data service interface; $C$ represents the incoming data, that is, the original code;$R$is the operation result:

20

$F=〈f_1,f_2,f_3,f_4,f_5〉.$

$F$ is divided into $f_1$, $f_2$, $f_3$, $f_4$, $f_5$ five steps:

21

$R=〈R_e,R_a,R_{n_1},R_{n_2}〉.$

$R$ includes edge node information, arc node information, operand information and operator information.

The specific steps of data service interface are:

22

$C^{\text{'}}=f_1\left(C\right),$

where $f_1$ stands for preprocessing operation, $C$ is the original code, $C^{\text{'}}$ is the code after deleting preprocessing statements, comments, spaces and macro replacement:

23

$y=〈T,A〉=f_2\left(C^{\text{'}}\right).$

$f_2$ represents lexical analysis operation, the result $y$ is lexical unit $〈T,A〉$, (TokenName, AttributeValue).

24

$I=f_3\left(C^{\text{'}},y\right),$

where $f_3$ represents semantic analysis operation, to match $C^{\text{'}}$ with $y$ for type check.

25

$z=AST=f_4\left(I\right),$

where $f_4$ represents the operation of generating an abstract syntax tree, and the abstract syntax tree $AST$ will be obtained.

26

$R=f_5\left(z\right).$

Finally, the abstract syntax tree is analyzed in $f_5$, and send to different interfaces to get $R$.

4. Design of program complexity measurement technology based on OINK framework

In order to complete the program complexity measurement technology, the data acquisition module and complexity analysis module are designed based on OINK data interface. The data acquisition module is used to collect the necessary data required for complexity calculation, and the complexity analysis module is used to calculate the complexity data results. Finally, the data can be stored and queried through data management.

4.1. Design of program measurement data acquisition module based on OINK framework

Data acquisition module needs to complete two tasks: obtaining data onto the intermediate results of program understanding platform; and storing data onto the form defined by the data structure. The function structure of the data acquisition module is shown in Fig. 4.

Fig. 4Function structure of data acquisition module

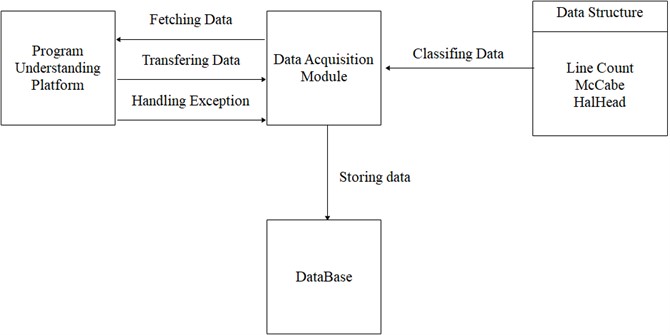
The function of the data acquisition module shown in Fig. 4 includes: collecting data from the program understanding platform, classifying and storing data according to different types of data structures, and storing all data into the database. If the system is abnormal in the process of collecting data, the data acquisition module will receive abnormal information and send it to the system for processing. The algorithm designed in the data acquisition module is shown in Fig. 5.

Fig. 5 shows the commonly used interface name in the algorithm. The retrieve function judges that the data to be collected by the system is for Line Count complexity measurement, McCabe complexity measurement, or HalSteadcomplexity measurement, according to the value of parameters; then collects different data. The search function can traverse the number of operators and operands from the abstract syntax tree, and can also obtain the number of nodes and arcs and the number of branch judgments from the program control flow diagram. The Send function to send the obtained data onto the complexity measurement system.

Fig. 5Design of data acquisition interface

4.2. Design of complexity measurement analysis module for target program

The system can support the measurement of Line Count Complexity, McCabe complexity and HalStead complexity, which are the core function of the system. The functional structure of its implementation is shown in Fig. 6.

Fig. 6Functional structure of measurement and calculation

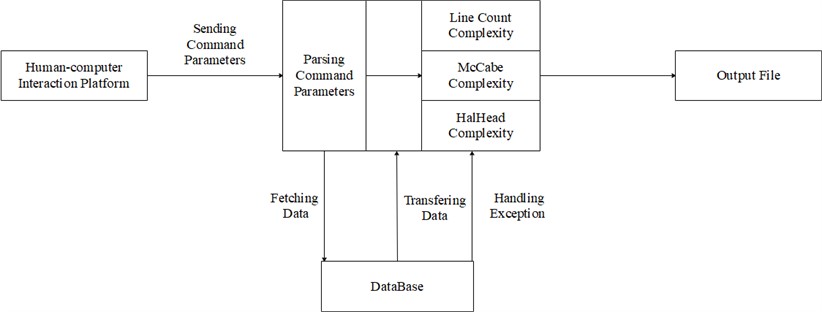
It can be seen from the Fig. 6 that the functional principle of the complexity measurement system is to send the command parameters for executing complexity measurement of the human-computer interaction platform, and analyze the types of command parameters through the analysis command parameter interface of the measurement system. There are three main commands of complexity measurement: Line Count complexity command, McCabe complexity command and Halstead complexity command. The measurement system retrieved the corresponding data measurement element from the database and output the result after calculation. If the required data cannot be found from the database, the system issues a prompt message of command execution failure.

The measurement and calculation functions of the system mainly include the calculation functions of Line Count complexity, McCabe complexity and Halstead complexity. Some specific differences between these three functions are shown in Table 1.

Due to the complexity of the algorithm structure, after describing the data acquisition algorithm of McCabe complexity measurement based on OINK platform, the next step is to analyze the algorithm of calculating cycle complexity measurement of McCabe complexity.

The algorithm mainly uses the cycle complexity to calculate the program control flow diagram. In formula, $n_c$ stands for cycle complexity, $n_a$ stands for the number of arcs, $n_n$ stands for the number of nodes:

27

$n_c=n_a-n_n+2.$

If the calculated cycle complexity is not equal to the result of judging the number of branches plus 1, it indicates that the input parameters of the algorithm are wrong, and the error information report is output. If the calculation is correct, the algorithm returns the value of cycle complexity.

Table 1Parameter comparison table of complexity measurement method

Parameters measurement	Line count complexity	McCabe complexity	HalStead complexity
Command parameters	001	010	011
Input	Code file	Program diagram information	Types of operators and operands
Output	Code line, blank line, comment line	McCabe measurement element	HalStead measurement element
Performance measuring	Physical scale of the program	Structure of program	Length of program
Data storage mode	Database	Database	Database
Exception handling	Support	Support	Support

5. Experimental analysis

After completing the design of program complexity measurement technology based on OINK framework, the experimental test is carried out. Firstly, load the test codes AutoCode.c and AutoCode2.c, and then the abstract syntax tree is generated based on the OINK framework. After that, the metadata required for program complexity measurement is obtained through the data service interface. Based on these measurement data, the McCabe measurement results, Line Count measurement results and Halstead measurement results of test codes are obtained. Finally, the measurement results are compared with the actual complex measurement data of test codes, as shown in Table 2, Table 3, Table 4 and Table 5.

It can be seen from Table 2 to Table 5 that the results calculated by the program complexity measurement technology based on the OINK framework are almost completely consistent with the real data, in which the Line Count measurement and McCabe measurement are completely consistent, and the accuracy of Halstead and standardized complexity measurement is close to 99.9 %. In order to more clearly illustrate the consistency of the two data, their histogram comparison and line chart comparison is shown in Fig. 7 and Fig. 8.

Fig. 7Histogram of comparison between experimental data and real data

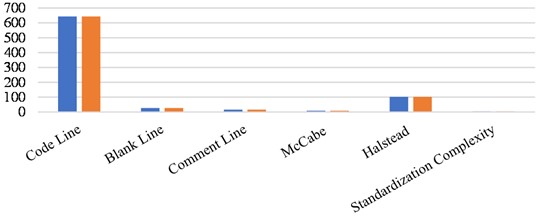
Fig. 8Line chart of accuracy comparison between experimental data and real data

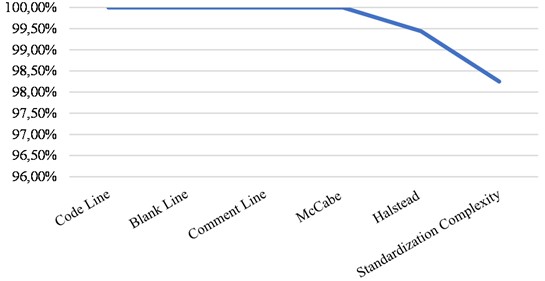
It is shown in the histogram that the experimental data are almost the same as the real data in the y axis, namely, the direction of the numerical axis. In Fig. 8 the curve direction of accuracy is almost parallel to 100 %. This further proves the rationality and accuracy of this technology.

6. Conclusions

The program complexity measurement technology studied in this paper uses OINK framework to statically analyze the program code. Firstly, based on the abstract syntax tree, the information statistics interface of edges and arcs of program control structure and the information statistics interface of program operators and operands are designed. Then, various types of measurement metadata are classified and summarized through the data acquisition algorithm, and the complexity results of the program are directly analyzed through the complexity measurement calculation module. Finally, the data is stored and queried through the measurement data management module.

This paper extracts the parameter factors required for code complexity analysis through abstract syntax tree, analyzes and calculates the complexity of software program structure by using Line Count measurement calculation method, McCabe measurement calculation method and Halstead measurement calculation method, and gives a comprehensive measurement report. At the end of this paper, the application testing environment is established, the application testing process is designed in detail, and then the complexity measurement test is carried out on the randomly selected program code. Through the analysis of the results, it shows the consistency between the system test results and the program complexity analysis results. Therefore, from the perspective of practical application, it proves the accuracy and feasibility of the program complexity analysis technology based on OINK proposed in this paper.