Study on chip shape and cutting force model of milling process in any direction of space

1. Introduction

The calculation of milling force for ball end milling cutter is an important step to estimate the dynamic stability and improve the surface quality in five axis machining process. Since there is an inclination angle between the cutter axis and the normal direction of the workpiece surface , so the milling force model is more complicated. Se [1] calculated the milling force in $x$, $y$ and $z$ directions with an inclination angle by using the coordinate transformation method. Altintas [2] calculated the start and exit angle of each cutting edge element with the existence of lead and tilt angle, thus aquiring the milling force. Fard [3] conducted experiments on the milling process of ball end milling cutter with the same lead angle and different tilt angles, and found that the lead angle had greater impact on the surface roughness. Chen [4] determined the optimized cutting direction by calculating the interference area between the tool and the workpiece. Urbikain [5] studied the dynamic stability in milling process under different lead and tilt angles, and found that the milling stability was very sensitive to the inclination angle. Yuan [6] designed the tool orientation without interference in the engagement, and thus generated a smooth machining path. Huang [7] achieved the optimization of tool posture by solving the problem of minimization of milling force in the direction of maximum blade deformation. Liu [8] implemented the micro milling experiment of KDP crystals and found that the surface roughness was lower when the positive lead angle was adopted. Chen [9] carried out an experiment study on the cutting surface roughness under different lead angles and found that the machining surface would have more defects when the lead angles were below 15°. In this paper, the chip thickness is calculated when the cutting edge line and chip boundary curve have one intersection point, two intersection points, one tangent point and no intersection point. Then the milling forces with inclination angle is calculated by using the differential method. By comparing the milling forces calculated by the method in the paper with those calculated by the Altintas model in the published literature, the validity of the proposed method is verified.

2. Milling model in any direction of space

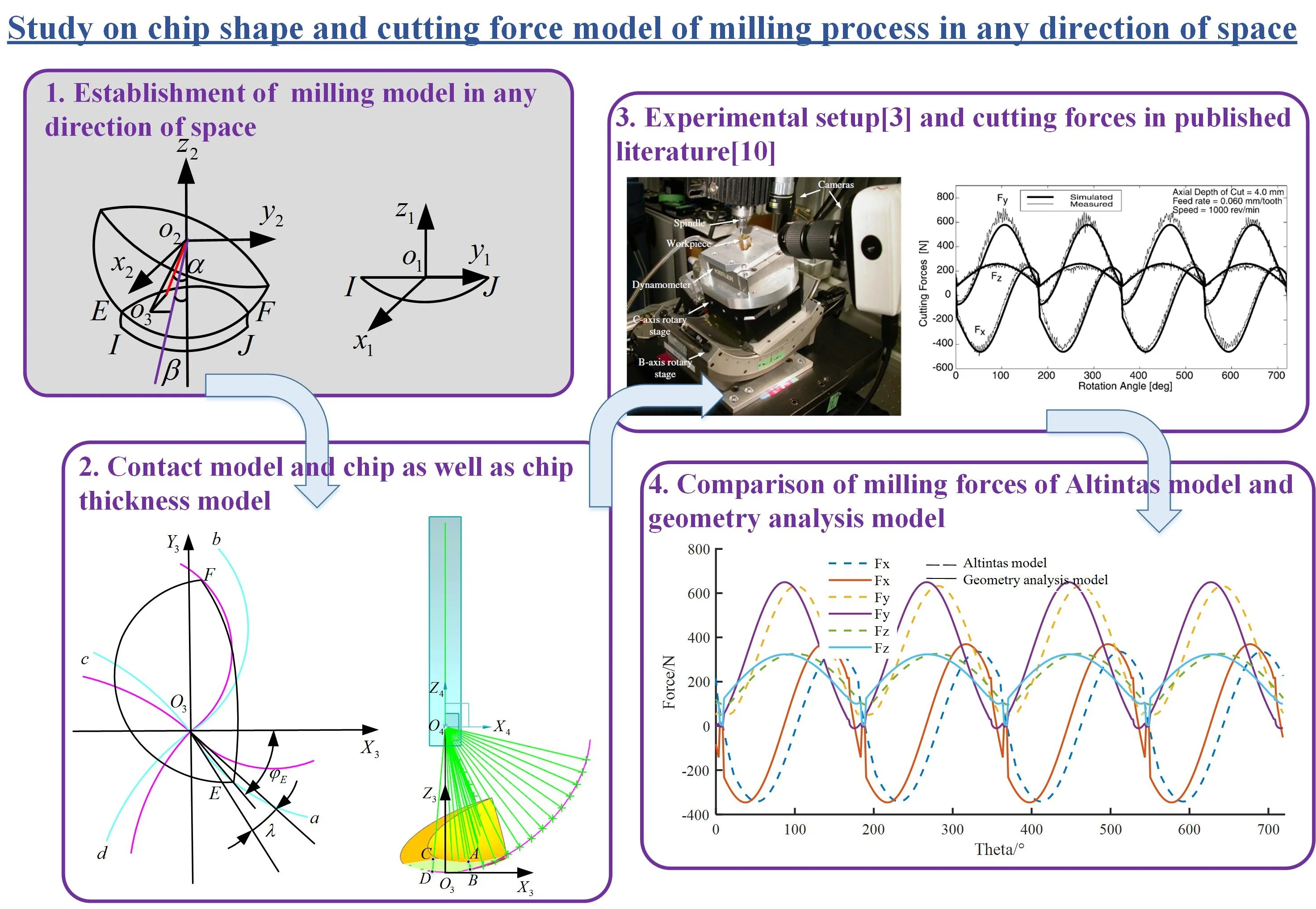
The milling model in any direction of space was established, and two inclination angles were adopted, including lead angle $\alpha$ and tilt angle $\beta$, as are shown in Fig. 1. The coordinate system $O_1{X}_1{Y}_1{Z}_1$ is established by taking the midpoint of line $IJ$ of the cutting area as the origin. Set the contact sphere between the ball end milling cutter and the workpiece after the first feed as sphere 1, and that after the second feed as sphere 2. The coordinate system $O_2{X}_2{Y}_2{Z}_2$ is established by regarding the center of sphere 2 as the origin, then the intersection of four edge lines of sphere 2 is the origin of coordinate system $O_3{X}_3{Y}_3{Z}_3$, and the axis $Z_3$ coincides with the cutter axis. Point $E$ and $F$ are the intersection points of sphere 1, sphere 2 and the workpiece surface.

Fig. 1Milling model in any direction of space

3. Geometry contact model between the edge line and boundary curve

The chip geometric model is shown in Fig. 2. In Fig. 2, when the chip thickness model only crosses the sphere, the geometry model is $AB$. When the chip thickness model crosses both the plane and the sphere, the geometry model is $CD$. Set up a coordinate system $O_4{X}_4{Y}_4{Z}_4$ paralleling to the coordinate system $O_3{X}_3{Y}_3{Z}_3$ at the center of the sphere 2. There are three types of contact cases between the cutter edge lines and chip boundary curves, which including intersection, tangency and no intersection, as are shown in Fig. 3 and Fig. 4.

Fig. 2Chip geometry model

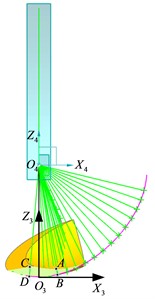
Fig. 3Intersection model

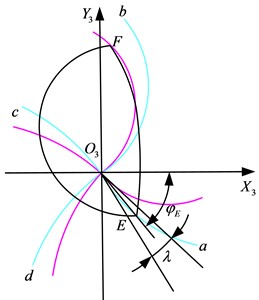
Fig. 4Tangent model

4. Chip thickness model

5. Milling force calculation

By calculating milling forces on different edge lines, the milling forces of the cutter in coordinate system $O_3{X}_3{Y}_3{Z}_3$ can be obtained. The cutter parameters and milling force coefficients [10] are shown in Table 1.

Thus, the milling forces in $x$, $y$ and $z$ directions can be obtained through integration,and the simulation results are shown in Fig. 5.

Fig. 5Milling forces for Fx, Fy and Fz: ap= 4 mm, lead angle α= 5°, tilt angle β= 10°, f= 0.06 mm

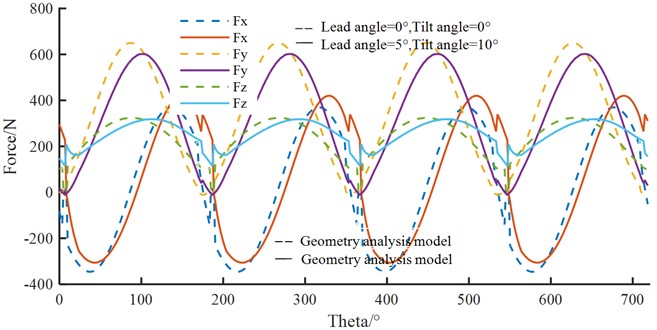
As can be seen from Fig. 5, when the lead angle is 5° and the tilt angle is 10°, the variation trend of milling forces in $x$, $y$ and $z$ directions is the same as that without inclination angle, but the amplitude of milling force in $x$ and $y$ directions are lower than that without inclination angle, while the amplitude of milling force in $z$ direction is basically the same as that without inclination angle. It shows that by increasing the lead and tilt angle in the milling process, the milling force can be reduced, thus changing the machining difficulty and improving the machining surface quality.

6. Experiment verification

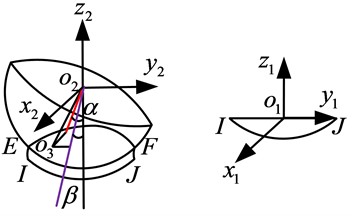
In order to verify the simulation results, the results of published literatures are used for comparison. The milling test can refer to the experiment in Fig. 6, the comparison results of simulations are shown in Fig. 7 and Fig. 8. An experiment designed by M. Javad Barakchi Fard of the reference [3] was used to describe the milling and testing process. The experiment is conducted on a five axis machining center in which the copper was processed by a two edge ball end milling cutter and the milling forces are measured through a Kistler sensor.

Fig. 6Experimental setup [3]

Fig. 7Measured and predicted cutting forces for slot cutting [10]

Fig. 8Milling forces of Altintas model and geometry analysis model

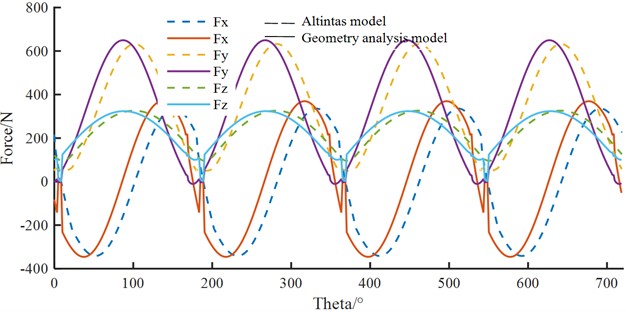
It can be seen from Fig. 8 that the milling forces calculated by geometric analysis method in this paper are basically consistent with those calculated by classical Altintas model, thus verifying the effectiveness of the method proposed in this paper. At the same time, by comparing the milling forces calculated by the classical Altintas model in this paper with the calculation and test results in the published literature [10], as is shown in Fig. 7, it can be found that they keep good consistency, which further verifies the rationality of the geometric analysis method adopted in this paper.

7. Conclusions

In this paper, the contact model between the cutting edge and chip in five axis machining process with lead angle and tilt angle is studied by geometric analysis method, and the milling forces are calculated. The results are compared with those of published literatures. The conclusions in this paper are as following:

1) When the lead angle is 5° and tilt angle is 10°, the change trend of milling forces in $x$, $y$ and $z$ direction is the same as that without inclination angle, but the amplitude of milling forces in $x$ and $y$ direction decrease compared with that of lead and tilt angle is 0°. Therefore, the milling forces can be reduced by changing the lead and tilt angle, thus improving the surface quality in the machining process.

2) The milling forces calculated by geometry analysis model are basically consistent with those calculated by Altintas model, which verifies the validity of the method adopted in this paper.

3) By comparing the calculation results of Altintas model in the paper with those of published literature, the rationality of the method in the paper is further explained.