Precision local anomaly positioning technology for large complex electromechanical systems

1. Introduction

Electromechanical systems (ES) are an indispensable part of aircraft on-board equipment, as well as an equipment to ensure the normal, safe and stable flight of the aircraft, which is the core system of the aircraft [1]. The safety of ES directly affects the safety of the aircraft. Therefore, the fault detection of aircraft ES is of great significance. Prognostics and Health Management (PHM) technology is an economical and efficient maintenance assurance method that includes fault diagnosis, prediction and health management of equipment. This approach is more commonly used in large complex ES and is often applied to aircraft ES [2, 3]. Data-driven PHM technology in ES is currently a hot research topic, and its core is based on data feature extraction and intelligent model classification to complete the evaluation of ES status. However, at present, the data-driven PHM technology has poor prediction effect on ES local faults, and the prediction accuracy and prediction efficiency are not satisfactory [4, 5]. This study innovatively added the Levy flight mechanism to the crow search algorithm and improved the position update strategy to enhance its global search ability; In addition, the multi resolution of wavelet decomposition is utilized to perform time-frequency localization analysis on signals in different frequency bands, without causing anomalies in signal extraction due to the size of the window, thus extracting abnormal signals more accurately. The study is intended to achieve precise local abnormality localisation and diagnosis for large and complex ES to ensure stable operation of ES and enhance aircraft safety. The research primarily introduces two breakthroughs. The first is to suggest a precise diagnosis method for small-scale, intricate ES local problems. The second point is the enhancement of the SVM’s diagnostic performance using the Improved Crow Search Algorithm (ICSA). The study’s format is broken down into four primary sections, the first of which is a review of pertinent research findings. In the second section, data features are extracted and an ES local defect diagnosis model is built using the wavelet packet energy spectrum. The method suggested in the study is validated in the third section. The study comes to an end in this section.

2. Related works

PHM technology is an intelligent technology that consists of several components, including defect detection, prediction, and intelligent decision-making. Machine learning technology has advanced significantly in recent years, offering concepts and strategies for the automated and thoughtful development of PHM technology. Intelligent PHM technology is widely employed in a variety of large and complicated ES to ensure the safe operation of ES. As a consequence, PHM technology has drawn considerable attention from researchers. Aljohani and Zhang used PHM technology for fault prediction in distributed systems, thus safeguarding patient ID privacy and preventing inference attacks [6]. Baur et al. explored the ways and application effects of PHM technology in machine tools, providing guarantees for the normal operation of machine tools, which also had a positive impact on the economic benefits of the plant [7]. In hopes of enhancing the service life of component drive systems, Oluwasegun and Jung presented a PHM technique based on machine learning to achieve intelligent failure prediction and health management of control component drive systems [8]. The disadvantages of PHM’s fault detection methods, which are not well suited for use in complex systems, were addressed by Wang et al., who also developed a self-supervised fault detection model based on learning algorithm-based data-driven fault detection model. The outcomes demonstrated that the model’s accuracy was superior to that of other algorithms [9]. Wang et al. avoided unexpected events and minimised financial losses by using PHM approaches for fault prediction and health management of rotating equipment. The efficiency of the spectral Lp/Lq parametric ratio and the spectral Gini index as health prediction indicators was experimentally proven to increase the fault prediction accuracy [10]. For the existing issue of high levels of noise in WT gearbox signals, which interferes with PHM data feature extraction, Pan et al. developed a data feature indication construction approach integrating deep trust network and self-organizing mapping (SOM). In order to forecast the service life of WT gearboxes, the enhanced particle filter (PF) was optimised using the fruit fly optimisation algorithm (FOA) [11]. Jimenez et al. evaluated the study findings about the integration of PHM technology into contemporary technical systems, illuminating the challenges and modifications that PHM technology is currently facing and offering suggestions and theoretical backing for their development [12]. To identify and monitor the operating status of the lithium-ion battery of electric vehicles and to assure the safety of electric vehicle drivers, Dong et al. presented a PHM system built around dynamic Bayesian networks [13].

SVM is a linear classifier and a discriminative model using supervised class learning approach. SVMs perform excellently in the categorization of small data samples. Moreover, SVMs may categorise non-linear issues by using kernel functions because of their straightforward structure, reduced computational requirements, and great degree of flexibility. Kurani et al. improved SVMs using the random forest (RF) and genetic algorithm (GA), then used the improved SVMs for stock forecasting. When the performance of an optimised SVM’s stock prediction was compared to that of an artificial neural network (ANN), the results indicated that the optimised SVM performed better [14]. In attempt to develop a prediction model for industry 4.0 engineering cost that was intelligent and accurate, Fan and Sharma integrated SVM and enhanced smooth support vector machine (ISSVM). Their experimental findings supported the model’s efficacy [15]. For the intelligent recognition of handwritten characters, Hamdan proposed a statistical SVM model and built an intelligent recognition model based on statistical SVM, offering a fresh perspective for the study of intelligent character recognition [16]. In hopes of foreseeing the water quality index of nearby rivers and give data support for local water quality management, Leong et al. fed water quality-related metrics into a least squares SVM [17]. Balasubramaniam used dermoscopic pictures to train, fit, and classify the SVM. He then used the SVM’s output classification results to help diagnose melanoma [18]. In order to help doctors anticipate the progression of hepatitis C and increase treatment success rates, Ghazal created a fine Gaussian SVM model. He then applied it to hepatitis C staging prediction [19]. The defect prediction diagnosis of self-driving automobiles was subsequently utilised with the enhanced SVM to increase their stability and safety [20]. Ahlawat and Choudhary combined convolutional neural network (CNN) and SVM to construct a high-precision classification model for high-precision intelligent recognition of handwritten digits [21].

As seen above, the PHM technology is being utilised widely across many ES, however there are still a number of fault detection issues that need to be resolved. SVM performs quite well in classification and prediction tasks, but the majority of recent research findings indicate that SVM still has a lot of flaws and need more optimisation. In the interest of enhancing the detection accuracy of ES faults and guarantee aircraft safety, the study suggests a better SVM and detects local faults of aircraft ES based on the improved SVM.

3. ES local fault detection model construction based on improved SVM

3.1. Wavelet packet energy spectrum based data feature extraction

With the rapid development of the economy and continuous technological progress, mechatronics technology has achieved unprecedented development. In the industrial field, electromechanical equipment is a very important equipment system. During the construction process, the control of electromechanical equipment and materials must be very strict, and every link must be strictly managed. Accurate positioning and testing of precision components in electromechanical equipment is an important factor in achieving normal operation of electromechanical equipment. The hydraulic actuator cylinder fault detection model based on ICSA-SSVM in this study has high accuracy and can efficiently and accurately achieve intelligent detection of hydraulic actuator cylinder faults, thereby ensuring the stable operation of aircraft ES and ensuring the safety of the aircraft. Fig. 1 depicts the fundamental steps of PHM technology, an affordable and effective way of maintenance assurance that is frequently used in aviation ES.

The hydraulic cylinder is a key part of the aircraft ES and is responsible for converting hydraulic energy into mechanical energy. When a fault occurs in the hydraulic cylinder, it will directly affect the normal operation of the whole ES. The schematic diagram of the simulation model of the hydraulic actuator is shown in Fig. 2.

The mechanical domain elements in the system are all standardized elements, and the modules can also be used in various fields, and the data between the modules can also be transmitted through the ports. Combined with the parameters set by the model, we can build a position feedback control system with higher accuracy and can obtain reliable operation data. The system is distinguished in different colors to identify data signals and control signals. The extraction of the fault signal of the hydraulic cylinder is very crucial to the accuracy of the fault detection. However, the fault signal data of hydraulic cylinders is often hidden at high frequencies and has a non-stationary character. Therefore, the traditional time domain analysis and frequency analysis methods are unable to extract the characteristics of the fault signal data. To address this problem, a method is proposed for the extraction of fault signal data features based on wavelet packet energy spectrum. Firstly, AMESim software is used to simulate and model the hydraulic actuator cylinder, and the parameters of the model are set as shown in Table 1.

Fig. 1Basic process of PHM technology

Fig. 2Simulation model of hydraulic actuator position control system

Table 1Parameter setting of hydraulic actuator simulation model

Parameter name	Unit	Value
Hydraulic actuator piston diameter	mm	30
Diameter of piston rod of hydraulic actuator	mm	20
Pumpage	ml/r	35
Servo valve natural frequency	Hz	50
Servo valve damping ratio	–	1
Rated current of servo valve	mA	200
Displacement sensor gain	–	10
Electrical gain 1	–	10
Electrical gain 2	–	250
Simulation time	–	12
Communication interval	–	0.05

In the AMESim-based hydraulic cylinder simulation model, the type of failure of the hydraulic cylinder can be set artificially by changing the values of the hydraulic cylinder parameters. These types of faults are, for example, leaks in the actuator cylinder, excessive load on the actuator cylinder, piston rod shaft offset of the actuator cylinder, etc. Signal analysis techniques such as the Fourier transform and wavelet transform are generally used in the extraction of fault signal characteristics. The Fourier transform is one of the more common signal feature extraction techniques, but this method cannot obtain the correlation between signal frequency and time, and requires the signal to be decomposed using a form of added window. In addition, as the window size is fixed, when the window size is not set properly, it will lead to the negative impact of signal feature extraction performance. Wavelet decomposition has the capability of multi-resolution analysis, and can analyse signals in different frequency bands in a time-frequency localised manner, thus analysing the detailed features of the signal and identifying and extracting abnormal signals. Wavelet decomposition’s primary application is the extraction of signal features based on the scaling and translating of the wavelet master function. A wavelet function with a finite length and a quick decay is called the mother wavelet function. If there is a productable function $\psi \left(t\right)$ with a Fourier transform of $\psi \left(\omega \right)$ on the function space $L^2\left(R\right)$. $\psi \left(t\right)$ is referred to as the wavelet mother function when it fulfils Eq. (1):

1

${\int }_{-\infty }^{+\infty }\frac{{\left|\psi \left(\omega \right)\right|}^2}{\omega }d\omega <\infty .$

Eq. (2) illustrates how to derive the wavelet basis function by scaling the wavelet mother function and applying a temporal translation:

2

${\psi }_{a,b}\left(t\right)=\frac{1}{\sqrt{\left|a\right|}}\psi \left(\frac{t-b}{a}\right),$

where $a$ is the scale factor and $b$ is the translation factor in Eq. (2). The indefinitely long trigonometric basis in the Fourier transform is replaced by a wavelet basis with a finite length and continuous decay in the wavelet transform method. The wavelet basis enables time-frequency analysis of the signal by effectively performing a Fourier transform with a real-time configurable window size. Fig. 3 depicts wavelet packet decomposition, which is based on wavelet decomposition.

Fig. 3 depicts wavelet packet decomposition, which is based on wavelet decomposition.

Fig. 3Wavelet decomposition and wavelet packet decomposition

a) Wavelet decomposition

b) Wavelet packet decomposition

In wavelet packet analysis, the scaling equation is as in Eq. (3):

3

$\varphi \left(t\right)=\sqrt{2}{\sum }_{n\in Z}{h}_n\varphi \left(2t-n\right),$

where, $h_n$ is the high-pass filter coefficients and the specific order of coefficients that make up the common orthogonal basis for the function space $L^2\left(R\right)$ and the scale function $\varphi \left(t\right)$. Eq. (3) displays the wavelet equation that was created using that Eq. (4):

4

$\phi \left(t\right)=\sqrt{2}{\sum }_{n\in Z}{g}_n\varphi \left(2t-n\right),$

where, $g_n$ is the low-pass filter coefficient. Suppose that Eq. (5) exists:

5

$u_0\left(t\right)=\varphi \left(t\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}{u}_1\left(t\right)=\phi \left(t\right).$

Hence, as indicated in equation, the orthogonal wavelet packet obtained in accordance with scale function $\varphi \left(t\right)$ can be written as a column of Eq. (6):

6

$\left\{u_n\left(t\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}n=\mathrm{0,1},2,\dots \right\}.$

Assuming that there is an observed signal, denoted $s\left(t\right)\in L^2\left(R\right)$, the coefficients of the projection can be calculated by Mallat fast wavelet decomposition, considering the discrete orthogonal wavelet transform operation as a projection lying on the orthogonal wavelet packet base. In practice, conjugate orthogonal filter banks are used to solve for this. For signals containing fault information in hydraulic cylinders, the wavelet transform has a good localisation capability. It is therefore possible to avoid the Gibbs benefit of the Fourier transform and to analyse sudden changes in the signal containing fault information. The study’s proposed wavelet packet transform method eliminates the wavelet transform’s drawbacks of unevenly dividing the frequency band and is able to analyse the signal more thoroughly while enhancing the time domain resolution of the signal. The above and Parseval’s theorem are used to create a four-step process for wavelet packet energy spectrum-based feature extraction. In order to obtain the $2^N$ frequency bands and the wavelet packet decomposition coefficients under each frequency band, noted as $p\left(l,i,j\right)$, the signal to be processed is first wavelet packet decomposed in layer $N$ using a suitable conjugate orthogonal filter set. The $j$ coefficients of the $i$th frequency band under the wavelet packet decomposition in the first layer are then obtained. Subsequently, a calculation is made to determine the energy value $E_l^i$ throughout all frequency bands, as shown in Eq. (7):

7

$E_l^i={\sum }_{j=1}^{n}p{\left(l,i,j\right)}^2.$

Then, each frequency band’s relative energy is determined. Ultimately, the relative energy that exceeds 85 % is chosen as the feature value based on the total percentage of energy in each frequency band. The extraction of the hydraulic actuator cylinder fault signal features is finished with the aforementioned.

3.2. Improved SVM-based fault detection model for hydraulic actuating cartridges

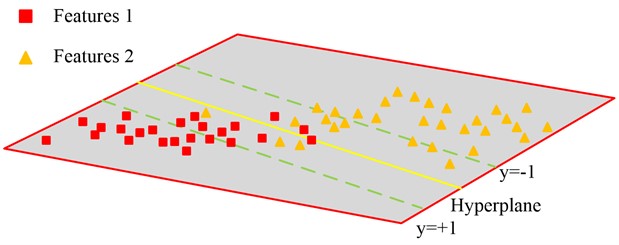
The study uses the extraction of hydraulic cylinder defect signal features in the aforementioned. The SVM is a popular classifier model that performs well in classification and identification issues involving limited samples, non-linearity, and high latitude. Finding a plane in the feature space where all feature points are separated and where the distance between the two points closest to the plane is the largest is the basis of the SVM feature classification principle. Fig. 4 depicts this plane, also known as the hyperplane.

However, the SVM has certain shortcomings that lead to the model’s low accuracy and efficiency, and its effectiveness in practical applications is not satisfactory. The SVM requires the introduction of a constraint when solving the problem. Therefore, it lacks convenience in application, and the accuracy and efficiency of the SVM model cannot be guaranteed. To address this problem, the study proposes strategies to optimise it. First, a two-dimensional parametrization is added to replace the position of the relaxation variables in the SVM solution equation, and $\psi /2$ is used to replace the position of the penalty factor in the SVM solution equation, at which point the SVM is solved as shown in Eq. (8):

8

$\underset{w,b,\xi }{\mathrm{m}\mathrm{i}\mathrm{n}\frac{1}{2}}\left({‖w‖}^2+b^2\right)+\frac{\psi }{2}\sum _{i=1}^N{\xi }^2,$

where, $w$ is the SVM’s weight parameter value, while $b$ is a constant in Eq. (8). Moreover, $\psi$ is a predetermined penalty parameter, while $\xi$ is the SVM’s slack variable. At this stage, equation displays the SVM’s limitations Eq. (9):

9

$y_i\left(w{x}_i+b\right)\ge 1-\xi ,$

where $x_i$, $y_i$ represents the data point $x$’s $i$th classification category and $i$th input vector feature, respectively, in Eq. (9). By substituting $\xi$ with a positive sign function modelled by a Sigmoid function in integral form, a model free of constraints is created. The model is shown as equation after a smooth factor $a$ is added to give it smoothness Eq. (10):

10

$\underset{\omega ,b,\xi }{\min }\frac{1}{2}\left({‖\omega ‖}^2+b^2\right)+\frac{\psi }{2}\sum _{i=1}^N{‖p\left(1-y_i\left(\omega x_i+b\right),a\right)‖}^2.$

Fig. 4Feature classification principle of SVM

Eq. (11) is then obtained by substituting the approximation function $f\left(x,a\right)$ for the Sigmoid function’s simulation of the positive sign function:

11

$\underset{\omega ,b,\xi }{\mathrm{m}\mathrm{i}\mathrm{n}\frac{1}{2}}\left({‖\omega ‖}^2+b^2\right)+\frac{\psi }{2}{\sum }_{i=1}^N{‖f\left(1-y_i\left(\omega x_i+b\right),a\right)‖}^2.$

The linear problem can be resolved using Eq. (1). In the hope of resolving a non-linear issue, a kernel function is introduced in Eq. (11), similarly to Eq. (12):

12

$\underset{\omega ,b,\xi }{\mathrm{m}\mathrm{i}\mathrm{n}\frac{1}{2}}\left({‖\omega ‖}^2+b^2\right)+\frac{\psi }{2}{\sum _{i=1}^N\left|\left|f\left(1-y_i\left[\sum _{i=1}^N{\alpha }_j{y}_{j}K\left(x_i,x_j\right)+b\right],a\right)\right|\right|}^2.$

Fig. 5 illustrates how Eq. (12) can be used to transfer a non-linear predictive classification problem into a high-dimensional space, making it a linear problem.

Fig. 5Mapping nonlinear problems to high dimensional space

a) Low dimensional nonlinearity

b) High dimensional linearity

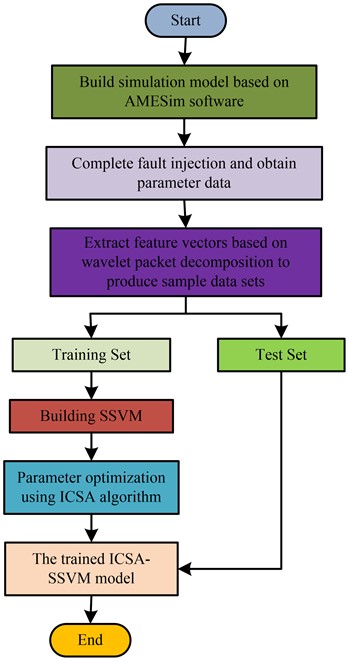
Fig. 6ICSA-SSVM hydraulic actuator fault detection model

In addition to the aforementioned, the SVM’s parameter setup requires improvement. The parameter selection and setting of the SVM is particularly significant since both the penalty factor and kernel function parameters of the SVM model must be established in advance. The values of these two parameters have a close influence on the results of the optimal classification hyperplane solution. The standard method for setting SVM parameters is to conduct manual tests to gradually identify the ideal values. Nevertheless, this approach takes a lot of time and is ineffective, and finding the right parameters to give the SVM model the optimum performance is challenging. In order to achieve this, the paper suggests using an Improved Crow Search Algorithm (ICSA) to look for the SVM’s ideal parameter values in order to enhance it. Tent chaotic mapping is used to generate the initial crow population in hopes of enhancing the diversity and search range of the crow population, as indicated in Eq. (13), in spite of the inadequacies of the CSA algorithm’s inadequate global search capabilities:

13

$y_{k+1}=\left\{\begin{array}{l}2y_k,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}0\le y_k<0.5,\\ 2\left(1-y_k\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}0.5\le y_k<1,\end{array}\right.$

where $y_k$ stands for the $k$th value in the chaotic sequence produced by the iterative Tent chaos mapping in Eq. (13). At this phase, the starting population is created, as seen by Eq. (14):

14

$X_0=X_{\mathrm{m}\mathrm{i}\mathrm{n}}+y_m\left(X_{\mathrm{m}\mathrm{a}\mathrm{x}}-X_{\mathrm{m}\mathrm{i}\mathrm{n}}\right),$

where $X_{\mathrm{m}\mathrm{a}\mathrm{x}}$, $X_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and $X_0$ in Eq. (14), respectively, stand for the maximum and minimum values of the search space and the starting crow population, respectively. The work adds the Levy flight mechanism to improve the CSA algorithm’s location update strategy and boost its ability to conduct global searches because the search step duration of individual crows has a significant impact on the algorithm’s search capability. The ICSA algorithm is used to determine the SVM model’s ideal parameters. Ultimately, the optimisation of the SVM is finished, and the ICSA-SSVM model is built to raise the precision and effectiveness of the SVM. Fig. 6 illustrates the fundamental steps involved in creating a hydraulic actuator cylinder defect detection and identification model based on ICSA-SSVM.

4. Performance analysis of the ICSA-SSVM fault detection model

The study uses the hydraulic actuator cylinder as an example and investigates the accurate identification of local abnormalities in big and complicated ES since abnormal fault detection of local components is currently rare in aviation ESPHM. An ICSA-SSVM based fault detection model is suggested in the interest of maximizing accuracy and efficiency in the detection and diagnosis of hydraulic cylinder problems. In order to verify the effectiveness of similar remaining life prediction methods, the data collected from the prediction data set published on the NASA Prognostics Data Repository (The website address is: https://www.nasa.gov/content/prognostics-center-of-excellence-data-set-repository) [22].

This experiment constructed the sample data set, and compared the effects of different similarity measurement functions, different information fusion methods and degraded mode matching on the experimental results. In this data set, the data of operation parameters of the hydraulic actucylinder in the life cycle is included. 65 % of the sample data in the sample data set is divided into training set, and the data is applied to the training of the hydraulic actuator fault detection model; another 35 % of the sample data is divided into test set, and the data is applied to the performance test of the hydraulic actuator fault detection model. The Extreme Learning Machine (FOA-ELM), which is based on an enhanced fruit fly optimisation algorithm, and the Optimised Adaptive Threshold Detection Model are two of the most recent state-of-the-art large complex ES local anomalous fault detection models (Implicit Association Test, IAT). First, Fig. 7 compares the convergence performance of the ICSA-SSVM model, the FOA-ELM model, and the IAT model during training. From Fig. 7, it can be seen that the error and loss values of the three models are rapidly decreasing at the beginning of the iteration, and the models converge rapidly. Among them, the Rate of convergence of the ICSA-SSVM model error and the Rate of convergence of the loss value are the fastest, which tend to be stable in 37 and 39 iterations, respectively, and the loss value is lower than the other two models. The IAT model has the slowest Rate of convergence, and can be stable only after 126 and 102 iterations respectively. The FOA-ELM model starts to converge at 63 and 64 times, respectively. It can be seen that the ICSA-SSVM model has stronger convergence.

Fig. 7Convergence performance of the model during training

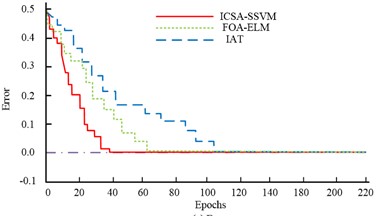
a) Error

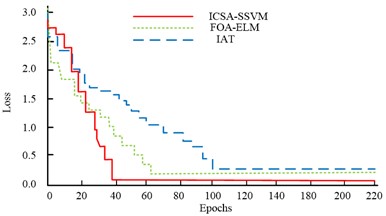
b) Loss

Fig. 8 shows the fitting of the sample data with the ICSA-SSVM model, FOA-ELM model, and IAT model during the training process. From Fig. 8(a), it can be seen that the ICSA-SSVM model has a fitting degree of 0.984 for the input sample data. From Fig. 8(b), it can be seen that the FOA-ELM model has a fitting degree of 0.966 for the input sample data, which is 0.022 less than the ICSA-SSVM model. From Fig. 8(c), it can be seen that the fit of the IAT model to the input sample data is 0.925, which is 0.059 less than the ICSA-SSVM model. It can be seen that the ICSA-SSVM model in this study has a high degree of fit with the input data, and has a higher accuracy in fault identification.

Fig. 8The fitting degree of the model to the input sample data

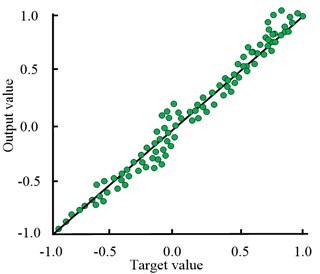
a) ICSA-SSVM

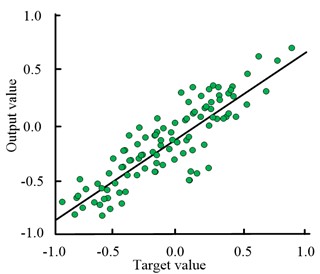
b) FOA-ELM

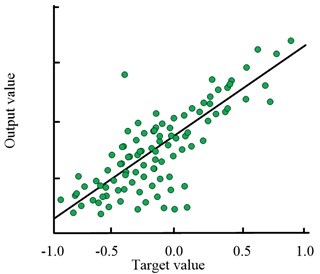
c) IAT

The test set was used to validate the fault detection accuracy of ICSA-SSVM model, FOA-ELM model and IAT model. However, because the measured data is affected by noise in real detection cases, so the robustness of low noise environment and high noise environment is analyzed. The results are shown in Fig. 9. As can be seen in Fig. 9, in the initial iteration, the ICSA-SSVM model, the FOA-ELM model and the IAT model are very close. After the iteration, there are obvious differences in the fault detection accuracy of the three models. Among them, the fault detection accuracy of the ICSA-SSVM model reached 99.16 %, which was 0.86 % and 1.35 % higher than the FOA-ELM model and the IAT models, respectively. In low noise environment, the accuracy of fault detection is higher than that in high noise environment. The above results show that the ICSA-SSVM model has higher fault accuracy and greater utility.

Fig. 9The fault detection accuracy of the model and the results of fault detection accuracy in high and low noise environments

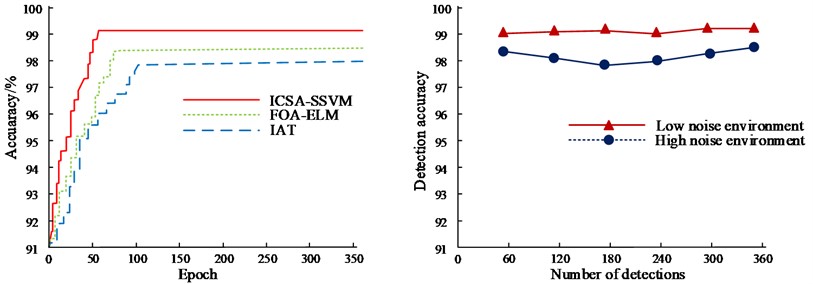
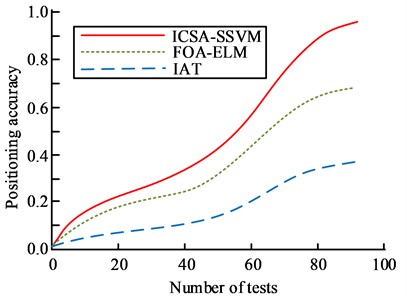
Fig. 10 shows the positioning accuracy curves of the ICSA-SSVM model, FOA-ELM model, and IAT model. As shown in Fig. 10, the positioning accuracy value of the ICSA-SSVM model is 0.96; The positioning accuracy value of the FOA-ELM model is 0.68. The positioning accuracy value of the IAT model is 0.37. The ICSA-SSVM model is 0.28 and 0.59 more than the FOA-ELM model and IAT model, respectively. It can be seen that the ICSA-SSVM model is more effective in the positioning accuracy and detection of electromechanical equipment, and has the highest accuracy.

Fig. 10Fault detection accuracy of the model

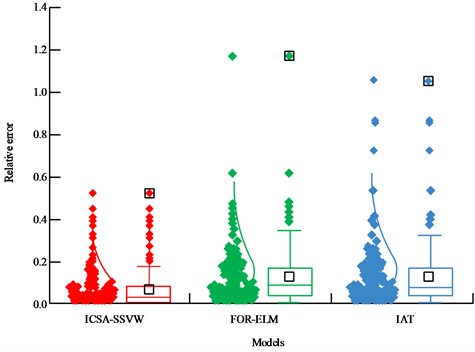
The relative error values of fault detection for the ICSA-SSVM model, FOA-ELM model, and IAT model were verified using test sets. The outcomes are displayed in Fig. 11. The greatest relative error value for the ICSA-SSVM model is 0.580. The highest relative error value for the FOA-ELM model is 1.201. The highest relative error value for the IAT model is 1.072. ICSA-SSVM model’s average relative error value is 0.082, which is 0.016 and 0.029 less than that of the FOA-ELM model and IAT model, respectively. The aforementioned findings demonstrate that the ICSA-SSVM model is more successful in accomplishing intelligent detection and identification of hydraulic cylinder faults because it has lower error values and higher accuracy in the detection and identification of hydraulic cylinder faults.

Fig. 11Relative error value of the model

Two metrics, F1 and Recall, were used to assess the performance of the ICSA-SSVM model, the FOA-ELM model, and the IAT model, as shown in Fig. 12. Fig. 12(a) shows that when the number of iterations is low, the F1 values of the ICSA-SSVM model, the FOA-ELM model, and the IAT model are quite near to one another. The F1 values of the ICSA-SSVM, FOA-ELM, and IAT models start to diverge dramatically after 15 iterations, with the ICSA-SSVM model improving its F1 value at a significantly faster rate than the FOA-ELM and IAT models. The F1 value of the ICSA-SSVM model, when the three models have fully converged, is 97.49 %, which is 0.72 % and 1.21 % higher than that of the FOA-ELM model and the IAT model, respectively. Fig. 12(b) shows that when the number of iterations is low, the Recall values of the ICSA-SSVM model, the FOA-ELM model, and the IAT model are relatively similar with only slight changes. The ICSA-SSVM model’s rate of rise in Recall values is much larger than that of the FOA-ELM and IAT models, and when the number of iterations surpasses 15, the Recall values of the ICSA-SSVM, FOA-ELM, and IAT models start to noticeably differ from one another. The ICSA-SSVM model’s Recall value was 94.52 % when the three models had fully converged, which was 0.68 % and 1.14 % higher than the values for the FOA-ELM model and the IAT model, respectively.

Fig. 12F1 and recall values for the model

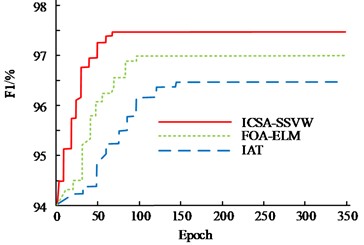
a) F1

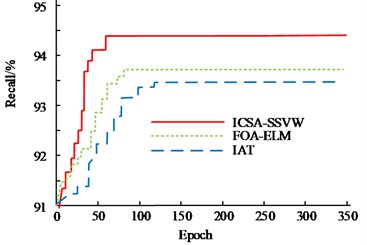
b) Recall

The combined performance of the ICSA-SSVM model, the FOA-ELM model, and the IAT model was evaluated using a displayed ROC curve. The ICSA-SSVM model’s AUC value, which is displayed in Fig. 13, was 0.986, which is 0.012 and 0.026. It can be seen that the hydraulic actuator cylinder fault detection model based on ICSA-SSVM in this study has high accuracy and can efficiently and accurately achieve intelligent detection of hydraulic actuator cylinder faults, thereby ensuring the stable operation of the aircraft ES and ensuring the safety of the aircraft.

Fig. 13Roc of the model

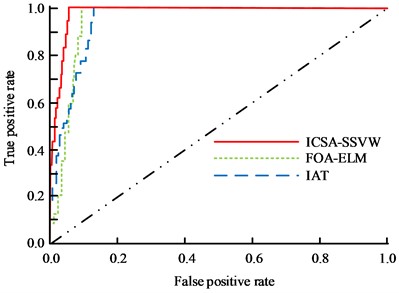
5. Conclusions

With the rapid development of the economy and the continuous progress of technology, mechatronics technology has achieved unprecedented development. In the industrial field, mechanical and electrical equipment is a very important equipment system. During the construction process, the control of mechanical and electrical equipment and materials must be very strict, and each link must be strictly managed. Accurate positioning and detection of precise parts of electromechanical equipment is an important factor in achieving normal operation of electromechanical equipment. Based on this, this study proposes the construction of an ICSA-SSVM model for precise local anomaly localization and detection of large-scale and complex electromechanical equipment, targeting the problem of faults in electromechanical equipment. The experimental results show that:

1) The fault detection accuracy of the ICSA-SSVM model is 99.16 %, which is 0.82 % and 1.48% higher than the FOA-ELM model and IAT model, respectively.

2) Compared with the FOA-ELM and IAT models, the average relative error value is 0.082, which is 0.016 and 0.029 lower than the average value.

3) The recall rate is 94.52 %, which is 0.68 % and 1.14 % higher than the FOA-ELM and IAT models, respectively.

4) The AUC value of the ICSA-SSVM model is 94.52 %, which is 0.68 % and 1.14 % higher than the FOA-ELM and IAT models, respectively.

From this, it can be seen that the model can intelligently identify defects in hydraulic actuator cylinders, and improve the accuracy and efficiency of electromechanical machines, ensuring the stable operation and safety of aircraft ES. However, the research on the health management of aircraft ES is not sufficiently in-depth, and it did not look into the service life prediction of local components of aircraft ES. In hopes of further enhancing aeroplane safety, it is necessary to provide methods for predicting the service life of components in following studies.