The optimization method of CNC lathe performance based on Morris sensitivity analysis and improved GA algorithm

2.1. Research on the optimization method of CNC lathe performance based on Morris sensitivity analysis

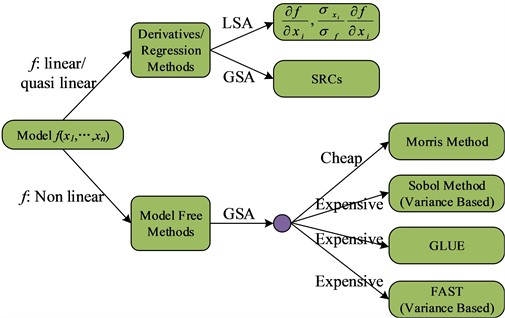
To solve multi-objective optimization problems, the parameters need to be optimized. However, the number of parameters involved in the engineering field increases the difficulty of calculation. Therefore, a sensitivity analysis of parameters is also needed before the actual parameter optimization to filter out the parameters with a greater degree of influence. The sensitivity analysis method of parameters mainly includes local analysis and global analysis. Local analysis is to estimate a single influencing factor when other influencing factors are guaranteed to be unchanged. The global analysis mainly includes the Sobol method, the Morris method, etc. [20]. The sensitivity assessment methods are classified according to the characteristics of the model, and Fig. 1 shows the classification results.

Among the above classification of sensitivity assessment methods, the Sobol method is more widely used, but the method has a high computational cost and is difficult to implement when there are more parameters. In mathematical models with more parameters, the Morris method is able to perform global sensitivity analysis and comparison with the least amount of computation. Therefore, the Morris method is chosen as the evaluation of parameter sensitivity in CNC lathe performance optimization in this study. Assuming that the system $y=y(x_1,x_2,...,x_i,...,x_k)$ contains $k$ parameters, the sensitivity of the parameters can be judged by analyzing the effect of the parameters on the results through Eq. (1):

Fig. 1Sensitivity analysis method

The Morris method requires mapping the parameters to the interval [0, 1], while random sampling is performed from $\{\mathrm{0,1}/\left(p-1\right),2/\left(p-1\right),\dots ,1-\Delta \}$. Where $p$ denotes the level of random sampling and $\mathrm{\Delta }=1/\left(p-1\right)$ denotes the amount of variation that has been determined in advance. The next step is to construct the random sampling matrix $B^{\mathrm{*}}$. While constructing the matrix $B^{*}$, the parameters mapped in the interval [0, 1] are remapped to the initial range. The sample data are then obtained based on the random sampling matrix to solve for the sensitivity values of the parameters. In the construction of the random sampling matrix $B^{\mathrm{*}}$, it is assumed that $D$ is a matrix of order $k$, and –1 or 1 is randomly selected as the diagonal element. $J_{k+1,k}$ denotes a matrix with all diagonal elements of order 1, and its size is $k+1\times k$ order. B denotes a triangular matrix with all diagonal elements of order 1, and its size is $k+1\times k$ order, see Eq. (2):

Also, a matrix $J^{\mathrm{*}}$ of size of order $k+1\times k$ is constructed in Eq. (3):

Assuming that the base value of the parameter $X$ is represented as $X_i^{\mathrm{*}}$, which is taken in $\{\mathrm{0,1}/\left(p-1\right),2/\left(p-1\right),\dots ,1-\mathrm{\Delta }\}$. Also, a matrix $Z^{\mathrm{*}}$ of size of order $1\times k$ is constructed in Eq. (4):

It is supposed that the random permutation matrix of order $k\times k$ is denoted as $P^{\mathrm{*}}$. There is only one element 1 in both rows and columns of this matrix. And the rest of the elements are 0. Then the representation of the random sampling matrix $B^{\mathrm{*}}$ is given in Eq. (5):

$J_{k+\mathrm{1,1}}$ represents a matrix of size of order $(k+1)\times 1$ and all elements are 1 in Eq. (5). Since the elements of the matrices $Z^{\mathrm{*}}$, $D$ and $P^{\mathrm{*}}$ are independent, mutually exclusive and random values, $B^{\mathrm{*}}$ is also a random matrix. In $B^{\mathrm{*}}$ matrix, each row represents a set of input parameters, while only one parameter is changing in two adjacent rows. The basic influence of each parameter can be calculated by combining Eq. (1). To improve the accuracy and credibility of the calculation results, the above calculation is repeated $n$ times. The Morris method defines two sensitivity indicators, $\mu$ and $\sigma$, to represent the influence of the input variables on the output. $\mu$ denotes the mean value, which is used to estimate the overall impact on the output with the test variables, and is calculated in Eq. (6):

where $r$ denotes the number of sampling times in Eq. (6) and $E{E}_{i,j}$ is the meta-effect of variable $i$ at the $j$th sampling. $\sigma$ denotes the standard deviation, which is used to estimate the effect of nonlinearity with the test variable on the output, as well as the effect caused by the interaction between the input variable and other output variables, which is calculated in Eq. (7):

A higher value of $\mu$ indicates a greater influence of the parameter on the system, and a higher value of $\sigma$ indicates a greater interaction between the parameter and other parameters.

In the experiment, the effects of 17 parameters such as the width of the main rib plate, the thickness of the main rib plate, the thickness of the horizontal partition plate, and the thickness of the horizontal partition plate on the performance of the CNC lathe were tested. In the Morris method, the value of parameter $p$ is crucial. If it is too small, it is difficult to ensure the credibility of the results, and if it is too small, it will increase the computational workload. Morris suggests taking an even number for p to ensure more uniform values for each parameter. The experiment shows that $p=$4 and $n=$10 can basically meet the analysis requirements. The larger the $\mu$ value, the more sensitive the parameter is to the bed, and the σ value reflects the interaction between the parameter and other parameters. Through research, it can also be found that overall, the larger the $\mu$ value, the higher the corresponding σ value. Through analysis, it can be seen that four structural parameters have a relatively small impact on the performance indicators of the bed. Therefore, removing these 4 parameters, only the remaining 13 structural parameters were sampled to prepare for the subsequent construction of an approximate model of the bed and optimization of bed parameters. In actual state, the bottom of the bed is fixed to the foundation with 8 bolts. Therefore, constraints are added to the bolts on the bottom surface of the bed, with zero degrees of freedom in all directions.

2.2. Research on CNC lathe performance optimization method based on improved GA algorithm

The approximation models can be used for the representation of implicit relationships in black-box problems based on known sample information. The use of approximation models enables the solution of complex problems in engineering problems, which shortens the product development cycle and can improve the efficiency. Due to the high complexity of CNC lathe structure, multi-objective optimization of nonlinear relationships needs to be realized. In the study of CNC lathe performance, a lot of time needs to be consumed for calculation every time. In the actual production process in the engineering field, intelligent algorithms are widely applied in the parameter optimization of machine tools. Genetic algorithm is widely used in the solution of multi-objective problems, but the current GA algorithm still needs to be optimized to improve the local search capability and solve the problem of premature optimization results. In this experiment, we propose to improve the traditional GA algorithm by using accelerated search strategy, namely Accelerated Search Strategy Genetic Algorithm (ASSGA). The training process of this method includes initial parent individual generation, individual evaluation, selection operation of parent individuals, segmented point crossing operation, two selections of random multipoint variants, local search operator, iteration, and introduction of accelerated search operator in Fig. 2.

Fig. 2Training flow chart of ASSGA algorithm

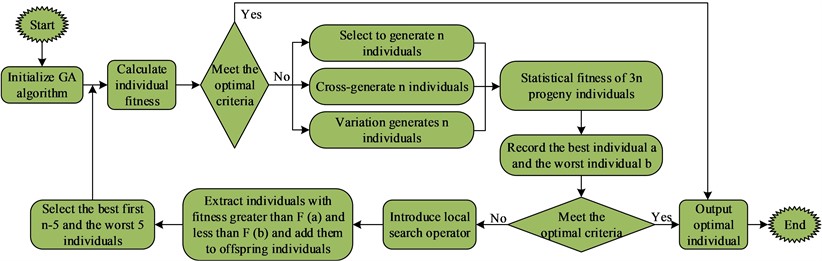
The ASSGA algorithm is able to select elite individual migration operators to achieve improved global superiority seeking ability. The method is able to increase the convergence speed of the algorithm while ensuring the superiority of the species. In the ASSGA algorithm, the worst genetic individuals obtained after selection are used in the mutation operation. By doing so, the diversity of the population can be improved, while enhancing the algorithm's global search ability and reducing the probability of premature occurrence. In addition, segmented point taking can ensure that the exchange of individual element information can occur evenly, and the introduction of local operators can enhance the local search ability of ASSGA algorithm. BP neural network can be well used for the prediction of production quality index parameters in the engineering field, but the traditional BP algorithm tends to fall into local optimum and has the defects of long model training time and slow convergence speed. Therefore, in this study, the combination of ASSGA algorithm and BP algorithm is used to obtain the model ASSGA-BP to improve model parameter prediction's accuracy. The specific steps of the combination of ASSGA algorithm and BP algorithm include the following points. Firstly, training samples' number is set as $N$, including training samples ${\varphi }_1$ and ${\varphi }_2$ in Eq. (8-9):

In the unimproved GA algorithm combined with the BP algorithm, the fitness function used is the BP method, and the error is obtained by training in Eqs. (10-11):

Assuming that the adaptation function of the ASSGA algorithm combined with the BP algorithm is $F(\omega ,v,\lambda ,\theta ,\gamma )$, it is defined in Eq. (12):

Eq. (13) is the objective formula for ASSGA algorithm combined with the BP algorithm:

In Eq. (13), $\omega$ indicates the connection weights from the input layer to the middle layer, $v$ indicates the connection weights from the first hidden layer to the second hidden layer, $\lambda$ indicates the connection weights from the hidden layer to the output layer, $\theta$ indicates the threshold value of each neuron in the hidden layer, and $\gamma$ indicates each neuron's threshold value in the output layer. $d_{ik}$ denotes algorithm's desired output value and $y_{ik}$ denotes algorithm's actual output value. ASSGA algorithm and BP algorithm's combining process requires the input training sample ${\varphi }_2$, which is calculated in Eq. (14):

It is assumed that ${\varphi }_3$ is the test sample and its sample size is $M$. At the end of the calculation, the combination of parameters can be obtained by substituting ${\varphi }_3$ into Eq. (15) to test the generalization ability of the algorithm with this parameter:

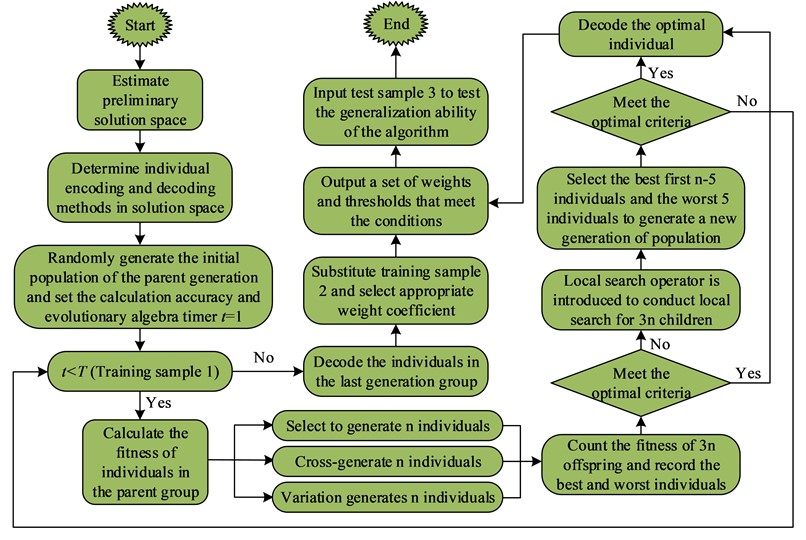
where $\epsilon$ denotes the error value in Eq. (15). If $E_3<\epsilon$, this combination of parameters is the optimal solution. Fig. 3 shows the flow of ASSGA algorithm combined with BP algorithm.

In the flowchart in Fig. 3, it mainly includes determining the initial solution space; determining the coding of individuals in the solution space and the decoding method; randomly generating the initial population of parents and setting the calculation accuracy and evolutionary generation timer; calculating the fitness of individuals in the parent population; performing the selection operation, crossover operation and variation operation of individuals in the parent population; counting the fitness of individuals in 3$n$ children and recording the best and worst individuals. The local search operator is introduced to perform local search on the 3$n$ children; the top $n-5$ optimal individuals and the worst 5 individuals are selected to generate the new generation population; the individuals in the last generation population are decoded; the appropriate weight coefficients are selected by substituting into the training sample 2; a set of weights and queues satisfying the conditions are output; finally, the testing sample 3 is input to test the generalization ability of the algorithm. The improved ASSGA algorithm can optimize BP algorithm's weights and thresholds. Since the improved ASSGA algorithm does not need the gradient information required by the traditional method, as long as the function is solvable, then the combined algorithm can operate properly. The improved ASSGA method can improve the generalization ability of BP neural network and solve the problems such as local optimality in the traditional BP algorithm.

In the experiment, based on the traditional BP algorithm, the genetic algorithm was combined with the BP neural network. And the global search performance of the genetic algorithm was used to determine the initial weights and thresholds of the BP neural network, effectively overcoming the local convergence problem of the BP algorithm. Due to the improved genetic algorithm (ASSGA)'s search method, which does not require the gradient information required by traditional BP, it only needs to solve the function under constraints, and the algorithm can operate normally. The improved genetic algorithm has better global search ability, so it has a good effect on optimizing the weights and thresholds of BP neural networks. It can effectively solve the problems existing in traditional BP neural networks and improve the generalization performance of neural networks.

Fig. 3Flow chart of ASSGA algorithm combined with BP algorithm

2.3. Simulation analysis of CNC lathe performance optimization method based on Morris sensitivity analysis and improved GA algorithm

The performance optimization effect of the CNC lathe was demonstrated using the main rib plate of the bed as an example in the experiment. In the experiment, the wall thickness, rib height, and rib thickness of the bed were used as a set of design variables, and the sensitivity method was used to analyze the impact of changes in structural parameters on the dynamic performance of the bed. The sensitivity diagram for height optimization of vertical and triangular bars in the main reinforcement plate is shown in Fig. 4.

In the experiment, parameter optimization was carried out on the arrangement of the rib plates. By changing the value of the rib plate parameters, calculation and analysis were conducted to obtain a sensitivity map of the rib plate parameters on the deformation of the bed, in order to obtain better rib plate structural parameters.

In order to test and evaluate the application of Morris sensitivity analysis with improved GA algorithm in CNC lathe performance study, ASSGA-BP was trained in the training set and the results were tested in the test set. Fig. 5 shows the accuracy and loss function results of the ASSGA-BP model in the training set and the test set. For the accuracy of the model in the training set, its success rate reached 92.3 % with the final loss function value of 0.09 when trained to the 20th batch; the success rate of the model in the test set when trained to the 20th batch reached 89.6 % with the final loss function value of 0.15.This is because the ASSGA-BP can select elite individual transfer operators to achieve the goal of improving global optimization ability. This method ensures the superiority of species while also improving the convergence speed of the algorithm.

Fig. 4Optimization of bed rib plate

a) Vertical ribs of the bed

b) Height of bed vertical reinforcement

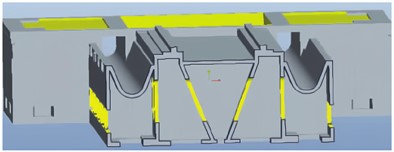
c) Triangular ribs of the bed

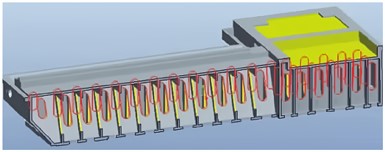
d) Height of triangular ribs on the bed

Fig. 5Accuracy and loss function results of ASSGA-BP method

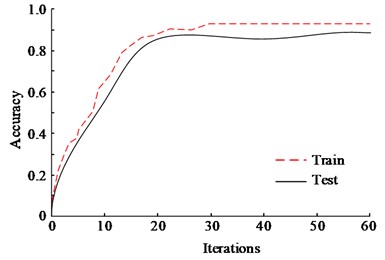
a) Accuracy

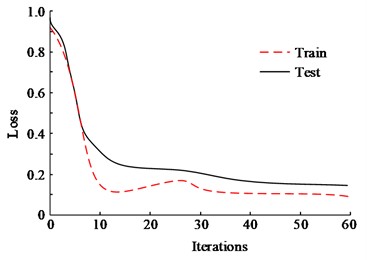
b) Loss

The ASSGA-BP method was compared and analyzed with the traditional GA and BP algorithms, and GA-BP algorithms [21]. The loss function values between the different methods were compared in the experiments, and the results are shown in Fig. 6(a). The loss function value of GA model is 0.25, BP model is 0.25, GA-BP model is 0.24, and ASSGA-BP model is 0.18. The loss function values of GA model, BP model, and GA-BP model are high relative to the loss function value of ASSGA-BP model. The root-mean-square error can be used to describe the dispersion of the samples, and the comparison of algorithm accuracy can be performed in the algorithm performance comparison. The root-mean-square error accumulation was used simultaneously in the experiments for the GA and BP algorithms, and GA-BP algorithms for comparative analysis, and the results are shown in Fig. 6(b). From the Figure, the root mean square error cumulative sum of GA, BP, and GA-BP method are all greater, which proves that the ASSGA-BP is highly accurate [22-23]. This is because in the ASSGA algorithm, the worst genetic individual obtained after selection is used for mutation operations. Through this approach, the diversity of the population can be improved, while enhancing the global search ability of the algorithm and reducing the probability of premature phenomena. In addition, segmented point selection can ensure that the exchange of individual element information can occur evenly, and the introduction of local operators can enhance the local search ability of the ASSGA algorithm.

The experimental validation of the recall rate of different algorithms was performed using datasets 1 to 6, each dataset contains 70 sets of data. Fig. 7(a) shows the recall results of ASSGA-BP and GA-BP. The recall rate of the ASSGA-BP model is significantly higher in four data sets. Although the GA-BP model outperforms the improved RBF network on two datasets, observing the area of the recall images of the two algorithms on the radar plot, it is found that the area of ASSGA-BP is larger, i.e., ASSGA-BP model shows a better recall than the GA-BP model overall. Fig. 7(b) shows the results of the recall rate comparison between the ASSGA-BP model and the GA model, and ASSGA-BP performs better than the GA network on every data set, and the difference between the two recall rates reaches up to 0.40, which indicates that the ASSGA-BP model steadily outperforms the GA network in terms of recall rate.

Fig. 6Cumulative comparison results of loss function values and root mean square error of different methods

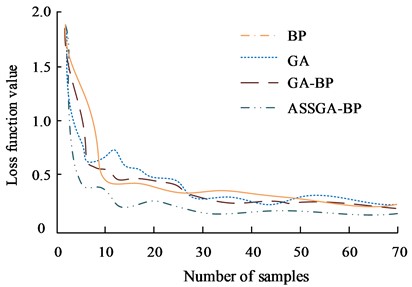
a) Loss function value

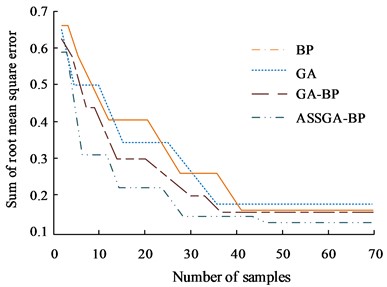
b) Sum of root mean square error

Fig. 7Recall performance of the improved ASSGA-BP algorithm

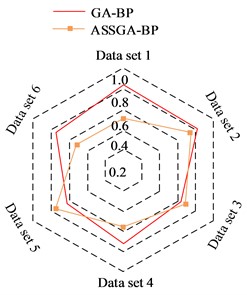
a) Recall results of ASSGA-BP and GA-BP

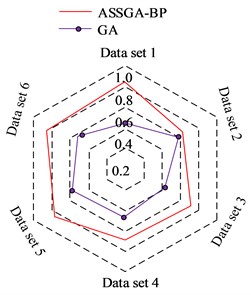
b) Recall results of ASSGA-BP and GA

Fig. 8(a) depicts the results of the specificity and sensitivity of ASSGA-BP and GA-BP model, while Fig. 8(b) shows the results of the improved ASSGA-BP model compared with the GA model. ASSGA-BP's specificity is always higher, with the difference reaching up to 10 %. When the data complexity is low, GA-BP’s specificity is lower. However, as data complexity increases, ASSGA-BP and GA-BP's difference gradually decreases. GA’s sensitivity is lower when data have low complexity. At this time, ASSGA-BP and GA-BP's difference is not obvious. As the data complexity rises, the sensitivity of the ASSGA-BP model decreases significantly less. This is because improving the ASSGA algorithm does not require the gradient information required by traditional methods. As long as the function is solvable, the combined algorithm can operate normally, thus reducing the computational difficulty of the algorithm.

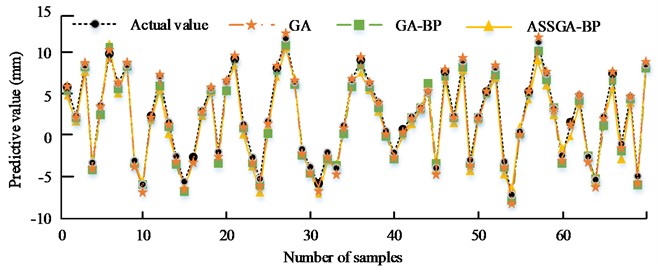
The results of GA model, GA-BP model and ASSGA-BP model for CNC lathe performance prediction are compared in Fig. 9. Compared with the real values, ASSGA-BP’s prediction accuracy model is higher. About the predicted value and real value's highest error, GA is 0.45 mm, GA-BP is 0.37 mm, and ASSGA-BP is 0.28 mm. It indicates that the accuracy of ASSGA-BP model is higher in CNC lathe performance prediction.

Fig. 8Comparison results of sensitivity and specificity of different algorithms

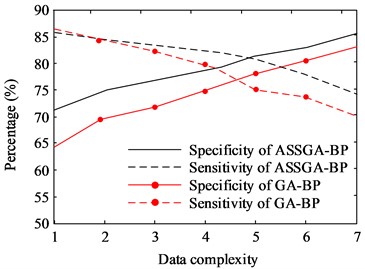
a) Results of ASSGA-BP and GA-BP

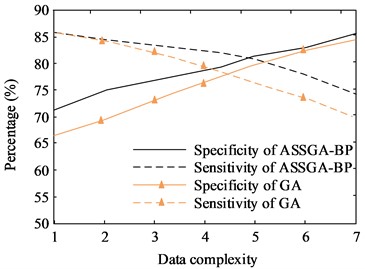
b) Results of ASSGA-BP and GA

Fig. 9Comparison of predictions of different methods

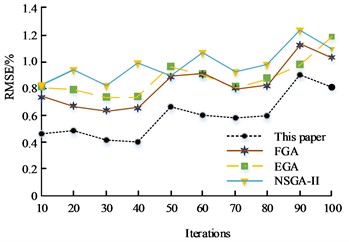
To further verify the performance of the multi-objective optimization method based on Morris sensitivity analysis with improved GA algorithm in the study of CNC lathe performance optimization methods, the model is experimentally compared with three commonly used multi-objective optimization models, FGA, EGA, and NSGA-II [24-26]. The comparison metrics selected in the experiment are MAE and RMSE, and the results are shown in Fig. 10(a) and Fig. 10(b), respectively. From Fig. 10(a), FGA’s highest MAE value is 1.43 %, the lowest MAE is 1.12 %, and the mean MAE is 1.21 % as the number of experiments increases. EGA's highest MAE is 1.39 %, the lowest MAE is 0.92 %, and the mean MAE is 1.12 %. NSGA-II's maximum MAE is 1.57 %, the lowest MAE is 1.20 %, and the mean MAE is 1.43 %. The highest MAE of the proposed model in this experiment is 1.12 %, the lowest MAE is 0.78 %, and the mean MAE is 0.91 %. From Fig. 10(b), as the number of experiments increases, FGA’s highest RMSE is 1.12 %, the lowest RMSE is 0.63 %, and the mean RMSE is 0.81 %. EGA’s highest RMSE is 1.20 %, the lowest RMSE is 0.72 %, and the mean RMSE is 0.83 %. NSGA-II's highest RMSE is 1.24 %, the lowest RMSE is 0.82 %, and the mean RMSE is 0.96 %. The highest RMSE of the proposed model in this experiment is 0.91 %, the lowest RMSE is 0.41 %, and the mean RMSE is 0.59 %. In the MAE and RMSE comparison experiments of different algorithms, the proposed model in this experiment is smaller than the three commonly used multi-objective optimization models, FGA, EGA, and NSGA-II.

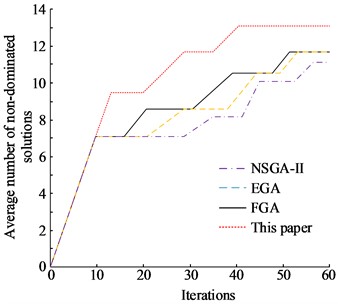
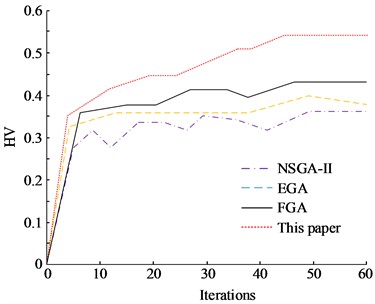
In multi-objective optimization, the number of non-dominated solutions can be used to indicate the superiority of a solution. Hypervolume (HV) is a metric used to indicate non-dominated solution’s dispersion and convergence. Among the multi-objective evaluation metrics applied in recent years, HV is one of the more commonly used metrics. If the value of HV is larger, it means that the final solution obtained is better. Fig. 11 shows the comparison results of the number of non-dominated solutions and HV for different methods. The results in Fig. 11(a) show that NSGA-II has the smallest number of non-dominated solutions, and EGA and FGA have the same number of non-dominated solutions. And the model proposed in this experiment is significantly better than the NSGA-II, EGA, and FGA algorithms in terms of both the number of final non-dominated solutions and the speed of reaching convergence. It shows that the method can maintain a high accuracy in solving the problem and also accelerate the convergence speed with better global search capability and local search capability. The HV values of each method are also calculated in Fig. 11(b). The convergence status of NSGA-II has a large volatility and the stability of the method is poor. The convergence status of EGA and FGA is relatively stable. The model proposed in this experiment can achieve faster convergence and the best stability of the convergence state.

Fig. 10Comparison of MAE and RMSE

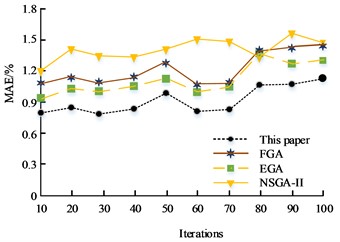
a) MAE / %

b) RMSE / %

Fig. 11Comparison results of the number of non-dominated solutions and HV for different methods

a) Comparison of average number of non-dominated solutions

b) Comparison of HV

In the comparison results of the specificity and sensitivity of the algorithm, as the data complexity increases, the decrease in sensitivity of the ASSGA-BP model is significantly smaller than that of the GA model and GA-BP model. In the comparison of the number of non-dominated solutions, the model proposed in this experiment is significantly better than the NSGA-II, EGA, and FGA algorithms in terms of both the final number of non-dominated solutions and the speed of convergence. It shows that the method can maintain high accuracy in solving, and can also accelerate the rate of convergence, and has better global search ability and local search ability. At the same time, this method can demonstrate high accuracy while ensuring high efficiency. These results confirm the superiority of the proposed method in the experiment.

In sensitivity analysis, the experiment mainly analyzed the impact of internal structural parameters of the bed on the quality performance indicators of the bed in Table 1. 17 structural parameters were initially selected in the experiment, and their range of variation was summarized from actual experience and casting process conditions. Based on the Morris sampling method, the parameters $k=$17, $p=$20, and the number of repeated experiments $n=$10 were set, resulting in a total of $n*\left(k+1\right)=$180 experimental schemes being generated for sensitivity analysis of each structural parameter.

Fig. 12Sensitivity analysis results of bed structure parameters

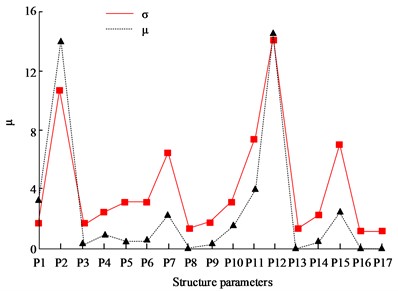
Fig. 12 shows the sensitivity calculation results between 17 bed structure parameters and quality performance indicators. The left and right vertical coordinates in each Figure represent the $\mu$ and $\sigma$ corresponding to the structural parameters. Among them, $\mu$ above zero indicates a positive correlation between the parameter and the indicator, while below zero it is the opposite. The larger the $\mu$ value, the more sensitive the parameter is to the bed, and the $\sigma$ value reflects the interaction between the parameter and other parameters. Through the graph, it can also be observed that the larger the $\mu$ value, the larger the corresponding $\sigma$ value. By analyzing Fig. 12, it can be seen that the top ten structural parameters that have a significant impact on the quality of the bed are P12, P2, P11, P1, P15, P7, P5, P10, P4, and P9. Among them, P8, P13, P6, and P17 have a sensitivity level of 0 to quality. Through comprehensive analysis, it can be seen that the four structural parameters P3, P6, P14, and P16 have a relatively small impact on the performance indicators of the bed. Therefore, removing these 4 parameters, only the remaining 13 structural parameters were sampled to prepare for the subsequent construction of an approximate model of the bed and optimization of bed parameters.