Abstract
Free vibration tests are attractive because they can be performed by means of a network consisting of few sensors temporarily installed on the structure in such a way to limit duration and cost of the experimental campaign. Additionally, free vibration tests are usually performed by introducing an initial perturbation that can induce a structural response significantly higher than the ambient excitation. This, in turn, allows to reduce the noise-to-signal ratio in the final measurements and/or to consider less stringent requirements about the technical specifications of the sensors. Since free vibration tests can provide accurate estimates of the modal parameters while being rather cheap and easy to implement, they have been performed in many applications, such as the experimental dynamic characterization of base-isolated buildings, masonry towers, ancient tie-rods, and bridges. An efficient and automatic computational framework is thus presented for the modal identification of bridges based on their free vibrations. The novel procedure proposed in the current work combines advanced signal decomposition techniques and a robust approach for damping identification. Two advanced signal decomposition techniques are considered, namely the Variational Mode Decomposition and the Empirical Fourier Decomposition. Experimental applications are then illustrated for roadway and railway bridges.
Highlights
- Dynamic identification of structural systems based on free vibrations.
- Extraction of unimodal components using advanced signal decomposition techniques.
- Automatic implementation of Variational Mode Decomposition and Empirical Fourier Decomposition techniques
- Robust identification of damping ratios and mode shapes.
- Dynamic identification of roadway and railway bridges.
1. Introduction
Free vibration tests are often performed for the experimental dynamic characterization of the structures. Such strategy is usually implemented at some point in time, periodically, and even after exceptional events. To this end, a sparse network consisting of few sensors is deployed on the structure to measure its free response following an applied load or an imposed displacement. Although such strategy does not allow to track continuously the evolution of the current structure conditions, it has some advantages. First, the larger intensity of the dynamic structural response makes possible the use of a sensor network designed to fulfill less stringent technical requirements. Moreover, the monitoring campaign takes a short time span, and a limited amount of data has to be collected and processed. In light of this, free vibrations tests have been reported for a large variety of applications [1-5]. In most field applications, free vibrations are extracted from the dynamic response induced in the structural system after an applied load or an imposed displacement. The original contribution of the current research consists with a novel procedure that aims at enabling the robust and automatic modal identification of bridges based on their free vibrations.
2. Proposed framework for modal identification using free vibrations
According to the proposed framework, all embedded relevant components are initially extracted from the recorded structural response. Among the available signal decomposition techniques, the Hilbert-Huang transform [6], also known as empirical mode decomposition, is widely adopted in structural monitoring applications [7]. Nonetheless, it has been found in previous applications that such technique is rather sensitive to noise and sampling. Therefore, two alternative advanced signal decomposition techniques are herein considered, namely the variational mode decomposition (VMD) technique [8] and the empirical Fourier decomposition (EFD) technique [9]. The decomposition of the recorded dynamic response into its relevant components allows to estimate the natural frequencies of the structure. Next, suitable strategies are implemented for the identification of damping ratios and mode shapes.
2.1. Variational mode decomposition
Let and be the time variable and the total number of components to be extracted from the recorded signal by means of the VMD technique, respectively. In the time domain, the VMD technique aims at extracting the relevant components from , also known as modes or intrinsic mode functions (IMFs), and estimating the corresponding central pulsation through the following steps:
1) the Hilbert-Huang transform is applied to compute the analytical signal for each 𝑘th IMF.
2) the frequency spectrum of the mode is shifted to baseband by mixing with an exponential function tuned to the respective estimated central frequency.
3) the Gaussian smoothness of the demodulated signal (i.e., the squared L2-norm of the gradient) is performed to estimate the bandwidth for each 𝑘th IMF.
Considering these steps, the signal decomposition according to the VMD technique is thus performed by looking for the solution of the following variational problem:
where and are the gradient operator and the L2-norm operator, respectively. The variational problem in Eq. (1) can be solved by using a quadratic penalty term and enforcing the constraints by means of the Lagrange multipliers technique. This leads to the following augmented Lagrangian function:
where is the quadratic penalty factor and is the Lagrangian multiplier whereas is the L2-inner product. The solution of the problem given in Eq. (1) thus corresponds to the saddle point of , which is obtained through a sequence of iterative sub-optimizations named alternate direction method of multipliers. From a computational standpoint, however, the complete final algorithm is more efficiently posed in the spectral domain rather than in the time domain. It is noted that the number of IMFs to be extracted and the penalty factor rule the performance of the VMD technique. Therefore, their value must be carefully determined for the accurate decomposition of the signal. In the present work, the procedure proposed by Mazzeo et al. [10] has been implemented for the automatic optimal tuning of both control parameters.
2.2. Empirical Fourier decomposition
The EFD technique is an adaptive decomposition method introduced recently by Zhou et al. [9] that consists of two main steps. First, a segmentation procedure produces frequency partitions of the frequency spectrum of the signal to be analyzed. Next, a zero-phase filter bank is required to perform the actual decomposition.
The segmentation process is carried out within a normalized frequency domain . Therefore, signal frequency lines must be also normalized. Initially, the boundaries of the contiguous frequency partitions are detected. The frequencies and are not required to be equal to and , respectively. The first frequencies corresponding to the largest maximum magnitudes detected in the signal spectrum are then sorted in descending order and are denoted as , whereas and . For each pair of consecutive frequencies and , the partition is determined by picking the frequency value at which a global minimum is attained as follows:
where is the Fourier spectrum amplitude between and whereas is the frequency variable. The second step of the procedure is the construction of a filter bank. Zero-phase filters are considered to avoid possible interference due to the transition phase, because it can cause mode-mixing effects. The zero-phase filter bank is based on the frequency partitions obtained after the segmentation (i.e., the boundary frequencies of each partition identify the cut-off frequencies). Therefore, let and be the Fourier transform of the signal to be analyzed and the zero-phase filter in the frequency domain, respectively. The generic filtered component has the following expression in the frequency domain:
The modal component can be finally expressed in the time domain by means of the inverse Fourier Transform operator, i.e. . Compared to the VMD technique, only one control parameter is involved into the EMD technique, which is the number of the frequency partitions . In principle, its value can be obtained from the frequency spectrum of the signal. Unfortunately, a simple counting of the peaks in the Fourier Transform of the signal is likely to produce a wrong segmentation because the signal spectrum is always noisy in practical applications. Therefore, an iterative procedure has been proposed to automatically tune the proper value of , in such a way to avoid both mode-mixing and mode-splitting phenomena [11].
2.3. Robust damping identification
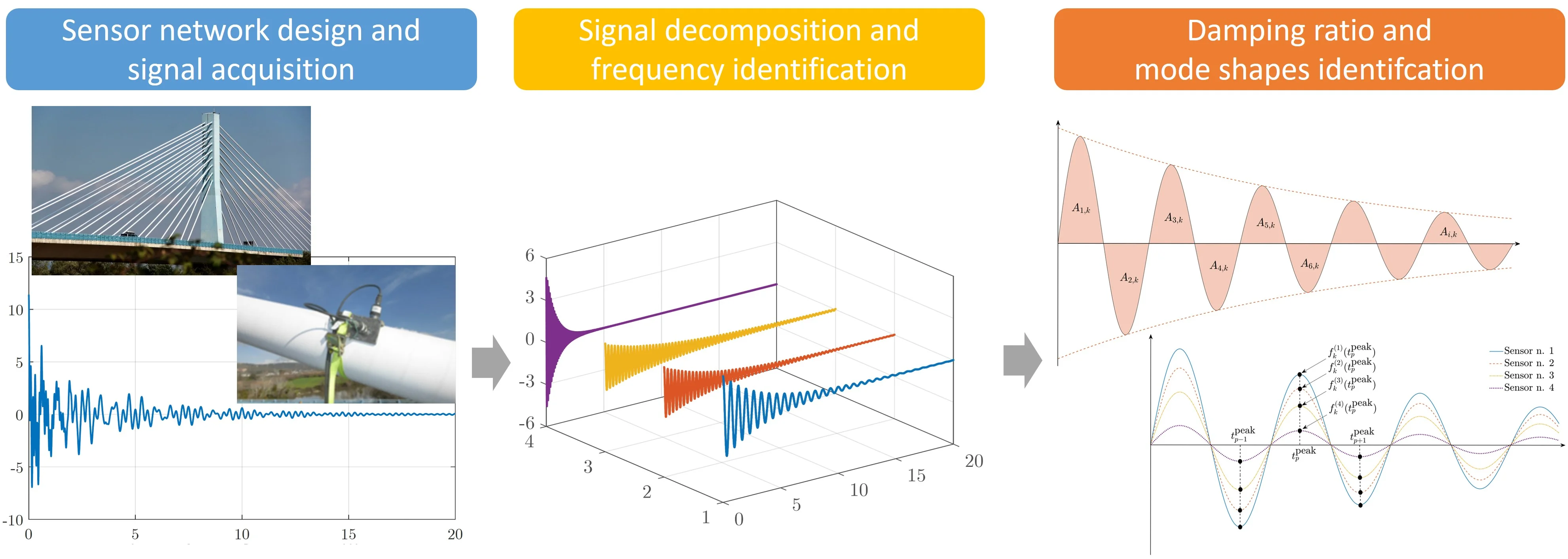
Once the th component has been extracted by means of either the VMD technique or the EMD technique, the associated modal damping ratio is evaluated by means of the area ratio-based method [12]. Let be the number of zero-crossing points in . It is possible to detect a total of regions enclosed between and the time axis with areas (see Fig. 1). So doing, the damping ratio is estimated as follows [12]:
where .
The application of the area ratio-based damping identification method is recommended since it is more robust against the noise as compared to the conventional logarithmic decrement technique.
Fig. 1Detection of the regions with area Ai,k defined by the 𝑘th signal component for the application of the area ratio-based damping identification technique
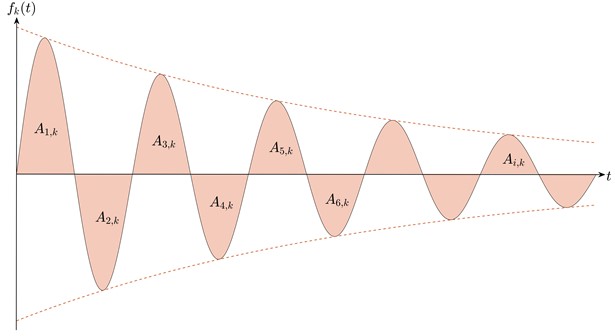
2.4. Mode shapes identification
The mode shapes are estimated by processing the free vibration response recorded from all available sensors after the decomposition accomplished via VMD technique or EMD technique [13].
Fig. 2A schematic diagram of a vibration separator
Particularly, the normalized 𝑘th mode shape vector is expressed as follows (see Fig. 2):
The effect of the noise can be mitigated by averaging the values in Eq. (6) for all peaks.
3. Experimental applications
The effectiveness of the presented framework for the modal identification of bridges based on free vibration response is investigated through preliminary applications to two experimental case-studies. The first application deals with the identification of natural frequency, damping ratio and force of the cables in the cable-stayed bridge crossing the Garigliano river (Fig. 3) [10, 14]. The second case-study is about the modal identification of a railway bridge (Fig. 4) [11]. Both the VMD technique and the EMD technique are employed for a comparative assessment of the final results.
Fig. 3Some preliminary results about the dynamic identification of the cables in a cable-stayed bridge

a) Picture
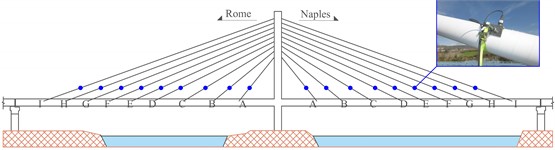
b) Sensors position
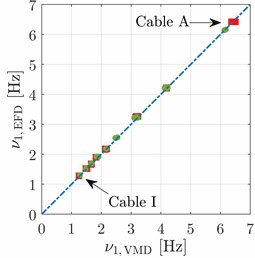
c) First natural frequency
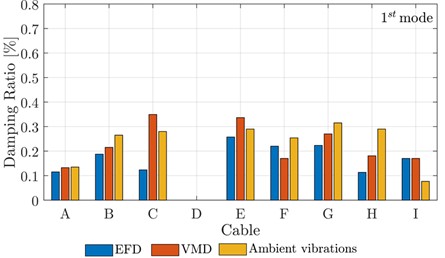
d) First damping ratio
Fig. 4Some preliminary results about the modal identification of a railway bridge

a) Picture of the bridge
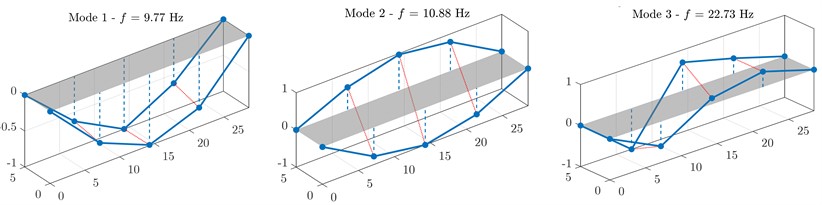
b) Mode shapes
4. Conclusions
This contribution has addressed the modal identification of structures from free vibration tests. Special attention has been paid to the decomposition of the recorded dynamic response of the structure, which is accomplished via Variational Mode Decomposition and Empirical Fourier Decomposition. The proposed procedure is also complemented with robust strategies for the identification of damping ratios and mode shapes. Preliminary experimental applications related to roadway and railway bridges have demonstrated the feasibility of the proposed identification methodology for practical applications.
References
-
S. Lagomarsino and C. Calderini, “The dynamical identification of the tensile force in ancient tie-rods,” Engineering Structures, Vol. 27, No. 6, pp. 846–856, May 2005, https://doi.org/10.1016/j.engstruct.2005.01.008
-
A. Athanasiou, N. D. Oliveto, and F. C. Ponzo, “Identification of first and second order models for the superstructure of base-isolated buildings using free vibration tests: A case study,” Soil Dynamics and Earthquake Engineering, Vol. 135, p. 106178, Aug. 2020, https://doi.org/10.1016/j.soildyn.2020.106178
-
W. Shi, J. Shan, and X. Lu, “Modal identification of Shanghai World Financial Center both from free and ambient vibration response,” Engineering Structures, Vol. 36, pp. 14–26, Mar. 2012, https://doi.org/10.1016/j.engstruct.2011.11.025
-
F. Magalhães, E. Caetano, Cunha, O. Flamand, and G. Grillaud, “Ambient and free vibration tests of the Millau Viaduct: Evaluation of alternative processing strategies,” Engineering Structures, Vol. 45, pp. 372–384, Dec. 2012, https://doi.org/10.1016/j.engstruct.2012.06.038
-
F. Lorenzoni, N. de Conto, F. Da Porto, and C. Modena, “Ambient and free-vibration tests to improve the quantification and estimation of modal parameters in existing bridges,” Journal of Civil Structural Health Monitoring, Vol. 9, No. 5, pp. 617–637, Nov. 2019, https://doi.org/10.1007/s13349-019-00357-4
-
N. E. Huang et al., “The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis,” Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, Vol. 454, pp. 903–995, 1998.
-
M. Barbosh, P. Singh, and A. Sadhu, “Empirical mode decomposition and its variants: A review with applications in structural health monitoring,” Smart Materials and Structures, Vol. 29, No. 9, p. 093001, Sep. 2020, https://doi.org/10.1088/1361-665x/aba539
-
K. Dragomiretskiy and D. Zosso, “Variational mode decomposition,” IEEE Transactions on Signal Processing, Vol. 62, No. 3, pp. 531–544, 2013.
-
W. Zhou, Z. Feng, Y. F. Xu, X. Wang, and H. Lv, “Empirical Fourier decomposition: An accurate signal decomposition method for nonlinear and non-stationary time series analysis,” Mechanical Systems and Signal Processing, Vol. 163, p. 108155, Jan. 2022, https://doi.org/10.1016/j.ymssp.2021.108155
-
M. Mazzeo, D. de Domenico, G. Quaranta, and R. Santoro, “Automatic modal identification of bridges based on free vibration response and variational mode decomposition technique,” Engineering Structures, Vol. 280, p. 115665, Apr. 2023, https://doi.org/10.1016/j.engstruct.2023.115665
-
M. Mazzeo, D. de Domenico, G. Quaranta, and R. Santoro, “An efficient automatic modal identification method based on free vibration response and enhanced Empirical Fourier Decomposition technique,” (Under review), 2023.
-
F.-L. Huang, X.-M. Wang, Z.-Q. Chen, X.-H. He, and Y.-Q. Ni, “A new approach to identification of structural damping ratios,” Journal of Sound and Vibration, Vol. 303, No. 1-2, pp. 144–153, Jun. 2007, https://doi.org/10.1016/j.jsv.2006.12.026
-
A. Bagheri, O. E. Ozbulut, and D. K. Harris, “Structural system identification based on variational mode decomposition,” Journal of Sound and Vibration, Vol. 417, pp. 182–197, Mar. 2018, https://doi.org/10.1016/j.jsv.2017.12.014
-
C. Maruccio, G. Quaranta, L. de Lorenzis, and G. Monti, “Energy harvesting from electrospun piezoelectric nanofibers for structural health monitoring of a cable-stayed bridge,” Smart Materials and Structures, Vol. 25, No. 8, 2016.
About this article
The work of Giuseppe Quaranta was carried out within the RETURN Extended Partnership funded by the European Union Next – GenerationEU (National Recovery and Resilience Plan – NRRP, Mission 4, Component 2, Investment 1.3 – D.D. 1243 2/8/2022, PE0000005).
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
