Study on the vibration characteristics of deep groove ball bearings under time-varying loads

1. Introduction

The crank-slider mechanism is a typical mechanism widely used in internal combustion engines, air compressors, grinding machines and other machines. The connecting pins, which is subjected to large radial loads and high-frequency movements, are one of the key components of the crank-slider mechanism. In order to ensure the strength of the connecting pin, reduce friction and wear during its working process, deep groove ball bearings are usually used as the support parts. Thus, the bearings will bear periodic variable loads, which will produce vibration and noise during high-speed operation.

Therefore, the study of bearing vibration characteristics has been widely concerned by scholars at home and abroad. Yu [1] established a multi-degree-of-freedom model of bearing system and analyzed the influence of factors such as waviness wave number on bearing vibration characteristics. Li [2] established a multi-degree-of-freedom deep groove ball bearing system and studied the effects of sliding characteristics and time-varying loads on bearing vibration. Jain [3] studied the effect of radial clearance on the nonlinear vibration characteristics of the bearing system. Kong [4] investigated the vibration response of the bearing system to the extra contact force generated by local defects of the bearing. Xu [5] presented a general methodology for dynamic modeling and analysis of planar multibody system containing deep groove ball bearing with clearance, and obtained the multibody contact dynamics response characteristics of the ball bearing by calculation.

From the existing literatures, it can be seen that the load used in the dynamics analysis system of rolling bearings is an hypothetical static load or dynamic load, thus, there is a great deviation between the research results and the actual situation, and it is difficult to characterize the actual performance of the bearing. In order to solve the above problems, the author puts forward a new idea based on the deep groove ball bearing used in the crank-slider mechanism of punching machine. This paper is organized as follows. Section 2 introduces the method of obtaining time-varying external load on inner ring of deep groove ball bearing. In Section 3, a brief discussion of the dynamic for deep groove ball bearing is presented. In Section 4, numerical results for presented methods are obtained and discussed. Finally, the conclusions are presented in Section 5.

2. Time-varying external loads on the inner ring of deep groove ball bearing

Fig. 1 is the schematic diagram of the crank slider mechanism of a punching machine. The slider is located right below the fixed hinge $A$, and is subjected to upward stamping resistance $F$. The center of mass and relative position of each component are shown in Fig. 1.

Fig. 1Sketch of crank-slider mechanism of punching machine

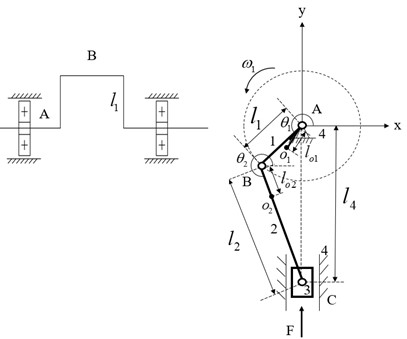
In the coordinate system $xAy$ shown in Fig. 1, force analysis is carried out on the three moving members, and their force equilibrium equations in the x and y directions and moment balance equations of rotation around the center of mass are established. The integrated mechanism dynamic equation can be expressed as:

where, $R_{ijx}$ and $R_{ijy}$ are components of the support reaction force $R_{ij}$ of member $i$ on member $j$ ($i$, $j=$ 1, 2, 3, 4) in $x$ and $y$ direction, respectively. $m_k$ ($k=$1, 2, 3) is the mass of member $k$. ${\epsilon }_1$ and ${\epsilon }_2$ are the angular acceleration of the crank and the connecting rod, respectively. $a$ is the acceleration of the slider. ${\ddot{x}}_{oi}$ and ${\ddot{y}}_{oi}$ arecomponents of the acceleration of the center of mass of element $i$ in $x$ and $y$ direction, respectively. $J_1$ and $J_2$ are the rotational inertias of the crank and the connecting rod, respectively. $A_i$ is the coefficient, $A_1=l_1\sin {\theta }_1-l_{o1}\sin \left({\theta }_1+{\theta }_{1p}\right)$, $A_2=l_1\cos {\theta }_1-l_{o1}\cos \left({\theta }_1+{\theta }_{1p}\right)\text{,}$$A_3=l_{o1}\sin \left({\theta }_1+{\theta }_{1p}\right)\text{,}$$A_4=l_{o1}\cos \left({\theta }_1+{\theta }_{1p}\right)\text{,}$$A_5=l_{o2}\sin {\theta }_2$, $A_6=l_{o2}\cos {\theta }_2$, $A_7=(l_2{-l}_{o2})\sin {\theta }_2$, $A_8=(l_2{-l}_{o2})\cos {\theta }_2$. The meaning of each symbol is shown in Fig. 1.

By solving Eq. (1), the change law of the support reaction force at hinge A can be obtained. Thus, the time-varying external load on the bearing inner ring is periodically variable in a movement cycle, the bearing will inevitably produce strong vibration.

3. Dynamic equations for deep groove ball bearing

3.1. Bearing system model and dynamic equations

Taking the deep groove ball bearing used in the fixed hinge A for an example, the bearing structure is shown in Fig. 2. The contacts among the ball, the inner and outer races are simplified as a spring-mass system, as shown in Fig. 2.

Fig. 2Sketch of crank-slider mechanism of press machine

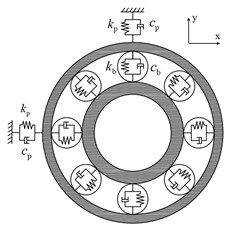
According to the bearing system model shown in Fig. 2, the corresponding dynamic equations in $x$ and $y$ directions can be expressed as:

2

$m_{ei}{\ddot{x}}_i+F_x+F_{c,x}=0.5R_{14x},m_{ei}{\ddot{y}}_i+F_y+F_{c,y}=0.5R_{14y},$
$m_o{\ddot{x}}_o+c_P{\dot{x}}_o+k_P{x}_o-F_x-F_{c,x}=0,m_o{\ddot{y}}_o+c_P{\dot{y}}_o+k_P{x}_o-F_y-F_{c,y}=0,$

where, $m_{ei}$ and $m_o$ are the equivalent mass of the inner and outer races, respectively. $c_P$ and $k_P$ are the damping and stiffness coefficients between the bearing outer race and housing. $F_x$ and $F_y$ are components of the radial contact force among the ball, inner ring and outer races in the $x$ and $y$ direction, respectively. $F_{c,x}$ and $F_{c,y}$ are components of the damping force between the inner and outer races in x and y direction, respectively. $m_{ei}$ is calculated as:

3

$m_{ei}=m_i+m\frac{\left(l_1-l_{o1}\right)}{l_1}+0.5m_x,$

where, $m_i$ is the mass of the bearing inner race, $m_x$ is the mass of the crankpin.

3.2. Contact force

The bearing inner and outer rings will produce relative displacement in the working process. Their position relationship is shown in Fig. 3. According to the local contact Hertzian theory, the load-deformation relation for point contact between ball-raceways for the ball j can be written as follows:

4

$F_{rj}=k_b{\left({\delta }_j^{1.5}\right)}_{+},$

where, $k_b$ is the total contact stiffness coefficient among the ball, inner and outer raceways contacts. ${\delta }_j$ is the total deformation of the ball $j$. The subscript "+" indicates that when ${\delta }_j$ is greater than zero, the ball is loaded giving rise to a restoring force $F_{rj}$. If ${\delta }_j$ is smaller or equal zero, the restoring force $F_{rj}$ is set to zero. $k_b$ can be computed as:

5

$k_b=\frac{1}{{\left(1∕k_i^{2∕3}+1∕k_o^{2∕3}\right)}^{1.5}},$

where, $k_i$ and $k_o$ are the stiffness coefficients of inner and outer races, can be obtained using [6].

${\delta }_j$ can be computed as:

6

${\delta }_j=\left(x_i-x_o\right)\cos {\theta }_j+\left(y_i-y_o\right)\sin {\theta }_j-0.5P_d),$

where ${\theta }_0$ is the initial angle of balls, here ${\theta }_0=0$. $\omega$ is the angular velocity of the pin. $r_b$ and $R_b$ are the curvature radius of inner and outer raceway, respectively. $O_i\left(x_i,y_i\right)$ and $O_o\left(x_o,y_o\right)$ are the center of the inner and outer races, respectively. $P_d$ is the initial radial clearance of bearing. ${\theta }_j$ is the angular position for the ball $j$, and can be defined by the following relation:

7

${\theta }_j=\frac{2\pi \left(j-1\right)}{N_b}+\frac{r_b}{R_b+r_b}\cdot \omega t+{\theta }_0,$

where $N_b$ is the number of balls in bearing.

Fig. 3Bearing inner and outer ring position relationship

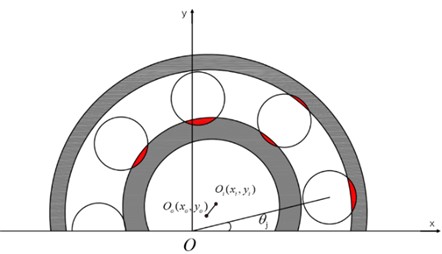
The total restoring force along the $x$ and $y$ direction is the sum of the restoring forces from each of the rolling elements, and can be defined by the following relation:

8

$\left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]={\sum }_{j=1}^{N_b}{F}_{rj}\bullet \left[\begin{array}{c}\cos {\theta }_j\\ \sin {\theta }_j\end{array}\right].$

4. Example

The crank-slider mechanism using in a punching machine is chosen as an example. The length, mass, rotate speed, and moment of inertia of crank are 6 mm, 0.3567 kg, 500 rpm, and 611.7 kg∙mm², respectively. The length, mass, and moment of inertia of connecting rod are 100 mm, 2.55 kg, and 7517.545 kg∙mm², respectively. The mass of slider is 16.7965 kg. The blanking force $P$ is 8964.8 N as 237°$\le {\theta }_1<$ 267°, other is 0 N. A pair of 6204 deep groove ball bearings exist between the crank 1 and the frame 4. The bearing parameters are obtained using [4].

Fig. 4 shows the load curve of the inner race of bearing. It is observed that the load will rapidly increase, and $R_{14x}$ is much larger than $R_{14y}$ when the slider enters the punching section.

Fig. 4Load curve of the inner race of bearing

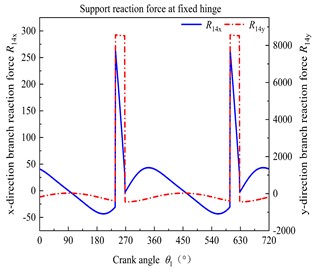
Fig. 5Track curve at the center of the inner race

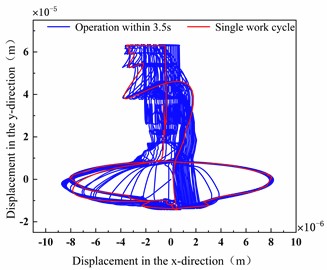
Fig. 5 shows the trajectory curve of the inner race center in a working cycle. It can be seen from Fig. 5 that the track curve of the inner race center is irregular, and has multiple mutations within a working cycle.

Fig. 6 shows the displacement frequency spectrum using the FFT processing. It is observed that the amplitude of vibration response in $x$ direction is obviously lower than that in $y$ direction.

Fig. 6Inner-loop FFT frequency domain response: a) x-direction, b) y-direction

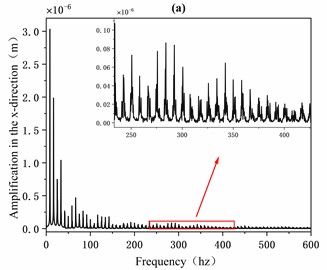
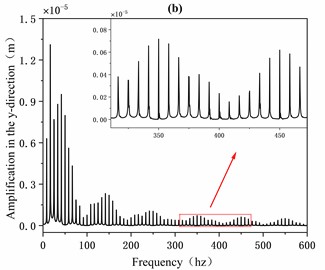
Fig. 7 shows the $x$ direction phase trajectory and the Poincaré cross-section mapping points of the inner ring under normal operation. In Fig. 7, the phase trajectories are circular curves of different dimensions. The Poincaré mapping points are distributed in the four parts, indicates that the motion of the inner race is unstable and shows quasi-periodic motion.

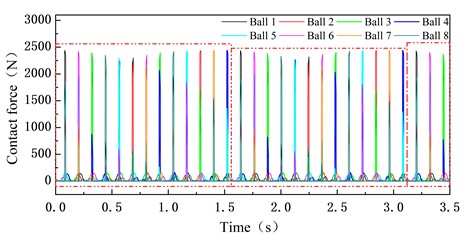
Fig. 8 shows the contact load of balls in two cycle periods during the normal operation. It can be showed that the contact loads of some of the rolling elements will change abruptly, and the impact on a certain point of the inner and outer races of the bearing will increase, and exacerbate the fatigue damage of bearing. Therefore, it can lay the foundation for the fatigue life prediction and the fault diagnosis of bearing.

Fig. 7The phase trajectory and the Poincaré map of the inner race

Fig. 8The contact load of ball element

5. Conclusions

A general methodology for dynamic modeling and analysis of deep groove ball bearing used in the crank-slider mechanism of punching machine is presented and discussed throughout this work. A typical deep groove ball bearing 6204 was used as a numerical example, to show the load characteristic of the inner race of bearing and the global dynamic behavior of the system.

From the results obtained, it was demonstrated that the load of the inner race of bearing changed periodically, and increased rapidly when the slider enters the punching section. The method presented can lay the foundation for obtaining the real load of bearing. Obviously, the motion of the inner ring is unstable and shows quasi-periodic motion. The dynamic performance of bearing inner ring in the time-varying load has a strong vibration, the inner ring, rolling body, outer ring, and other components are subjected to strong impact, which will cause the machine to produce noise during the working process and cause environmental pollution. Additionally, the equivalent constraint force on each ball obtained can be used for the strength checking and fatigue life prediction of bearing. The presented methodology provides a theoretic foundation for further research.