The influence of elastohydrodynamic lubrication on the stiffness of deep groove ball bearing

Zhang, Yu; Xie, Liyang; Lv, Xiao; Sun, Guohua

doi:10.21595/jve.2016.17002

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 November 2016

Check for updates

The influence of elastohydrodynamic lubrication on the stiffness of deep groove ball bearing

Yu Zhang¹

Liyang Xie²

Xiao Lv³

Guohua Sun⁴

¹School of Mechanical Engineering, Shenyang Jianzhu University, Shenyang, China

²School of Mechanical Engineering and Automation, Northeastern University, Shenyang, China

³Welding Technique and Technology Equipment Division, Shipbuilding Technology Research Institute, Shanghai, China

⁴Department of Mechanical and Materials Engineering, University of Cincinnati, Cincinnati, USA

Corresponding Author:

Yu Zhang

Cite the article Download PDF

Downloads 1842

WoS Core Citations 3

CrossRef Citations 6

Abstract

An accurate modeling of roller bearing element, considering the complex contact behavior and load conditions, is very important to the geared-rotor system design. This paper presents an enhanced bearing stiffness matrix for a deep groove ball bearing by including the elastohydrodynamic lubrication (EHL) effects in the ball-raceway contact. The bearing model is subjected to the coupled lateral-translational loads. The EHL contact is calculated by employing the multilevel method. Then, the EHL result was used to drive the relationship between the contact force and mutual approach. Moreover, the effect of the centrifugal inertial force on the ball elements resulting from the circumferential cage motion is considered. New equilibrium equations of the ball bearing considering the EHL contact model were established, and an enhanced bearing stiffness matrix was given. The dominant stiffness coefficients of deep groove ball bearing due to external loads under both lubricated and dry contact conditions are compared. Parametrical studies are also carried out to investigate the influence of the EHL on the stiffness matrix. Results show that the EHL has a negligible effect on the radial stiffness coefficients for all load conditions. However, the EHL has more influence on the rotational and coupling stiffness coefficients.

1. Introduction

In modeling the geared rotor-bearing systems, the rolling bearing effect can be easily incorporated into the system model by introducing the relevant bearing stiffness set [1-3]. Hence, it is highly desirable to develop an accurate stiffness model of rolling bearings to facilitate the dynamic analysis and system design. The mechanical contact linking the rolling element and raceway as the force path is the key factor affecting the bearing stiffness. The contact property is determined by the geometrical dimensions and material characteristics of contact bodies, such as ball/roller elements, inner/outer raceways and the existence of lubricants.

Elastohydrodynamic lubrication (EHL) is the common lubrication type in the rolling element bearings to guarantee a long lifecycle. However, most of the research work on the analytical modeling of bearing stiffness matrix normally neglects the EHL effect due to its complexity. The pioneering work on the dynamic modeling of rolling element bearings was done in more than 50 years ago by Jones [4], in which the radial and axial load-deflection relation of bearing was characterized by a nonlinear stiffness coefficient. Then, the spring features of ball bearing and its contribution to the vibration of the rotor were investigated by Shimizu and Tamura [5, 6]. The dry contact stiffness coefficients have been widely adopted in general geared rotor dynamic analysis, such as spur and hypoid geared rotor systems [3, 7-9]. The main contribution of lubrication film is only considered by decreasing the friction coefficients in multi-body dynamics analysis including rolling bearing and the effects of the fluid dynamics without quantifying the contact stiffness[10].

There have been some research efforts driven to understand the effects of the EHL film on the contact stiffness at the rolling element-raceway contact or bearing stiffness. The early study of EHL contact stiffness was performed by Wijnant [11], where an approximation formulation was proposed to describe the contact force and mutual approach for circular and elliptical EHL contacts. An implicit stiffness formulation for the EHL contact was further obtained and applied to investigate the effect of the lubricant on the dynamic behavior of rolling element bearings [12, 13]. Then, based on the observation that the EHL pressure resembles a pure hydrodynamic pressure for low loads while approaches to the dry Hertzian contact pressure for high loads, Wiegert [14] developed the EHL contact stiffness approximated by a series connection of a hydrodynamic and a Hertzian force element. Based on an elastohydrodynamic lubrication line contact-vibration model, Zhang [15] studied the stiffness and damping of oil film existed in the EHL contact region. The results showed that the oil film stiffness made less contribution to the total contact stiffness compared to the Hertzian contact stiffness. Very recently, Notato [16] suggested a polynomial relation for the dimensionless restoring force and mutual approach at the lubricated contact, establishing the first explicit force-displacement formulation at each contact. Later, a novel approximate relation for the EHL contact between ball element and raceway in deep groove ball bearing was proposed by Notato [10]. Nonato assumed that the EHL contact relation follows a unified behavior for a given constant inner speed, analogous to that of its equivalent dry contact, but shifted by a rather constant amount. It was reported that this contact assumption was validated indirectly by the laboratory rotor-bearing test. Moreover, the damping coefficient of the EHL contact was proposed. Then, a translational bearing contact dynamic model was derived by considering the stiffness and damping of the EHL film. Jacobs [17] experimentally investigated the formation of a lubricate film in a deep groove ball bearing and its effect on the bearing dynamics. The test results demonstrated that EHL has a weak effect on the radial stiffness coefficients.

In addition, there are quite a few contributions on the study of EHL for an abnormal lubricated bearing system with surface defects [18, 19]. The theoretical studies show that the contact stiffness under hydrodynamic condition is less than that under the Hertian condition with deep surface defects, and squeeze film damping operates most efficiently in the region of thicker films. Liu [20] calculated the time-varying contact stiffness between the roller and races due to the nonuniform surface waviness and investigated its effect on the vibration response of the lubricated roller bearing. Babu [21] analyzed the nonlinear vibration of an elastically deformable shaft at high rotational speeds supported on two lubricated angular contact ball bearings with surface waviness on races and balls, however, the detailed calculation process for the stiffness and damping of the lubricated contacts were not given, and the influence of the EHL on the bearing stiffness coefficients were also not investigated.

It is noted that the existing studies are mainly focused on the analysis of the contact stiffness for the lubricated rolling element and raceway contact under relatively low bearing speeds [10, 16]. There are no reported works in public on the discussion of the effect of the EHL on the bearing stiffness coefficients at high bearing speeds. Note, the centrifugal inertia force for rolling element should be considered at high bearing speed. In addition, only the radial stiffness coefficients of the lubricated bearing were considered in [10, 16]. The effect of the lubrication on the coupling stiffness coefficients proposed by Lim and Singh [22] to predict plate rigid-body angular motion or plate flexural motion as excited by shaft motion attracted little attention. There is a need to develop a comprehensive stiffness matrix used for characterizing the out-of-plane type motion given the bending motion on the shaft by considering the EHL and high speed effects. To fill in these gaps, an improved analytical bearing stiffness matrix considering both the EHL and high speed conditions is conducted in this work. In the first part of this study, the EHL contact was developed using the multilevel method proposed by Venner and Lubrecht [23]. Based on the numerical results of the EHL contact, an explicit contact force and mutual approach formula was derived considering the centrifugal inertia forces applied on ball element for low and high bearing speeds. These relationships are used on the establishment of the lubricated bearing equilibrium model describing the relation of bearing forces and displacements. An enhanced five-dimensional stiffness matrix of the lubricated bearing is given based on the comprehensive dry contact bearing stiffness matrix proposed by Lim and Singh [21]. Furthermore, the stiffness coefficients from both dry and lubricated bearings under different combinations of loads are compared, and the effects of EHL on stiffness coefficients are discussed.

2. EHL contact model

2.1. Definition of mutual approach

The schematic diagrams of dry contact and EHL contact are shown in Fig. 1. For the dry contact, the displacement of the load point $δ_{d}$ is equal to the elastic deformation $D_{d}$ at the contact center. However, for a lubricated contact, due to the hydrodynamic lift effect of fluid films, the displacement of the load point $δ_{c e n}$ is the difference of the elastic deformation $D_{c e n}$ and film thickness $h_{c e n}$ at the contact center:

1

δ_{c e n} = D_{c e n} - h_{c e n},

where, $δ_{c e n}$ is the mutual approach (the relative motion between two undeformed points within the contact bodies in the direction normal to the lubricated contact surface). Note the displacement of the load point $δ_{d}$ is the mutual approach for the dry contact.

Fig. 1Illustration of the mutual approach in dry and EHL contacts

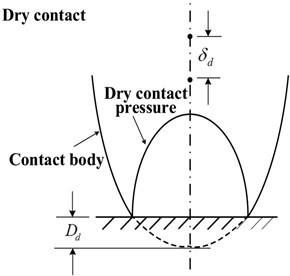
a)

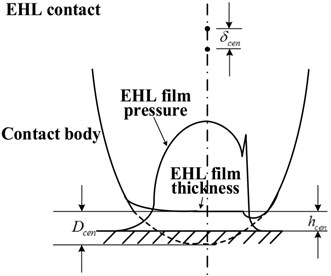
b)

2.2. Contact force and mutual approach relationship

Before incorporating the effect of thin film lubrication on the analysis of bearing equilibrium model and hence the bearing stiffness, an explicit relationship between the EHL contact force and the mutual approach is developed. Here, the method proposed by Nonato is adopted in this study. Nonato [10] assumed that the relation for lubricated ball element and raceway contact follows a unified behavior for a given constant bearing speed, similar as that for the dry contact, but shifted by a certain constant amount. Then, the following formulation was given [10]:

2

K_{E H L} δ^{n} + Δ Q_{E H L} = Q,

where $δ$ and $Q$ are mutual approach and contact force at the ball element-raceway contact, respectively. The stiffness coefficient $K_{E H L}$ , the exponent $n$ , the contact force constant $Δ Q_{E H L}$ can be obtained via a curve fitting of the data of contact forces and mutual approaches. This contact assumption has been validated indirectly by the results from a laboratory rotor-bearing test rig [10].

The geometry and material parameters of deep groove ball bearing and lubricant parameters are listed in Table 1. The chosen inner ring rotational speeds of bearing are 6308 r/min and 18924 r/min and the outer ring is fixed. Ignoring the gross slip at the rolling element-raceway contact, the linear speed $u_{m}$ at the center of ball element and the rotational speed of ball element $n_{b}$ about its own axis can be calculated as [25]:

3

u_{m} = \frac{π D_{m}}{120} n_{i} (1 - \frac{D_{b}}{D_{m}}),

4

n_{b} = \frac{D_{m} n_{i}}{2 D_{b}} (1 - {(\frac{D_{b}}{D_{m}})}^{2}),

where, $n_{i}$ is the rotational speed of bearing inner ring, $D_{b}$ is the diameter of ball element, and $D_{m}$ is the average of $D_{i}$ and $D_{o}$ which are inner and outer raceway diameter, respectively. The rolling speed $u r$ at the ball element-raceway contact in bearing and the centrifugal inertia force $F_{r}$ applied on ball element can be obtained by:

5

u r = \frac{2 π n_{b}}{120} D_{b},

6

F_{r} = \frac{2 m_{b} u_{m}^{2}}{D_{m}},

where, $m_{b}$ is the mass of ball element and its value is 0.02 kg. Based on the above Eqs. (3)-(6), the rolling speeds are $u r =$ 10 m/s and $u r =$ 30 m/s, respectively, corresponding to inner ring speeds of 6308 r/min and 18924 r/min, and the inertia forces applied on ball element are 40 N and 354 N, respectively.

For the bearing with a high speed, the centrifugal inertia force applied on ball element must be considered for the calculation of EHL behavior. The contact force range at the ball element and inner raceway contact varies from 600 N to 2000 N, and the outer raceway contact force is the summation of the inner raceway contact force and inertia force on ball element. Following the similar analysis by Nonato [10], the multilevel technique [22] is adopted to model the EHL contact, which is introduced to numerically evaluate the Reynolds equation governing the gap film flow. In order to achieve a better numerical convergence and reduce the discretization errors, the asymmetric integrated control volume scheme [25] is used to discretize the second-order partial differential Reynolds equation. The Roelands equation [26]is used for the viscosity-pressure relation, and the lubricant compressibility is modelled with the Downson and Higginson [27]. The discrete convolution and fast Fourier Transform (DC-FFT) scheme [28] is applied here to reduce the computation time of elastic deformation at EHL contact domain. A complete description of discretization and solution process of EHL problem can be found in [22, 24], and the application of DC-FFT scheme for solving elastic deformation is discussed in detail in [27].

Table 1Parameters for deep groove ball bearing and lubricant oil

Parameters	Value
Outer raceway diameter (mm)	82
Inner raceway diameter (mm)	48
Ball diameter (mm)	17
Number of rolling elements	8
Inner/Outer raceway groove curvature radius coefficient	0.54
Radial clearance (mm)	6×10^-3
Elastic modulus (Pa)	2.07×10¹¹
Poisson’s ratio	0.3
Atmosphere viscosity (Pa∙s)	9.6×10^-2
Pressure viscosity coefficient (Pa^-1)	1.82×10^-8

The elastic deformations and film thicknesses at the inner and outer raceway contacts are obtained by multilevel technology. The mutual approach for each contact is calculated by the Eq. (1). Based on the Eq. (2) proposed by Nonato [10], the contact force at each contact can be expressed as shown in Eq. (7) as the function of the mutual approach:

7

K_{i, o}^{} {(δ_{i, o}^{})}^{n_{i, o}^{}} + Δ Q_{i, o}^{} = Q_{i, o}^{},

where, the index $i$ and $o$ represent the inner and outer raceways contact, respectively.

It is worth noting here that a combine loaded deep groove ball bearing at high speeds acts as an angular contact ball bearing due to the effects of gyroscopic motion of the ball element, which can result in a little difference for the inner and outer contact angles. In this paper, the zero gyroscopic moment is assumed for each ball element, therefore, the inner and outer contact angles remain the same. Based on the assumption, the total mutual approach between inner and outer raceways at the position of a ball element can be obtained as follow:

8

δ = δ_{i}^{} + δ_{o}^{} = {(\frac{Q_{i}^{} - Δ Q_{i}^{}}{K_{i}^{}})}^{1 / n_{i}^{}} + {(\frac{Q_{o}^{} - Δ Q_{o}^{}}{K_{o}^{}})}^{1 / n_{o}^{}} .

Due to the centrifugal inertia force applied on the ball elements, the inner and outer raceways contact forces satisfy $Q_{o}^{} = Q_{i}^{} + F_{r}$ . Then, Eq. (8) can be rewritten as:

9

δ_{} = δ_{i}^{} + δ_{o}^{} = {(\frac{Q_{i}^{} - Δ Q_{i}^{}}{K_{i}^{}})}^{1 / n_{i}^{}} + {(\frac{Q_{i}^{} - Δ Q_{o}^{*}}{K_{o}^{}})}^{1 / n_{o}^{}},

here, $Δ Q_{o}^{*} = Δ Q_{o}^{} - F_{r}$ . Nonato assumed that the total mutual approach and inner raceways contact force follow the similar behavior to each individual contact. Therefore, the Eq. (9) is rewritten as:

10

δ = {(\frac{Q_{i}^{} - Δ Q}{K})}^{1 / n},

11

K δ^{n} + Δ Q = Q_{i} .

The inner raceway contact force at the ball element position is related to the total mutual approach between the raceways by the above Eq. (11). Actually, for the dry contact, the same expression as Eq. (11) can also be derived when the centrifugal inertia force acting on the ball element is considered. Therefore, Eq. (11) is used here to describe the contact relation at the ball element position between the raceways for both lubricated and dry contacts.

For the above given rolling speeds (or bearing speeds), the total mutual approaches due to different inner raceway contact forces are shown in Fig. 2 for both lubricated and dry contacts. The unknown coefficients in Eq. (11) can be obtained by fitting the inner raceway contact forces and the total mutual approaches. A least square method is employed to find the unknown coefficients as shown in Tables 2. The coefficients of determination for these fits are almost 1, which represent that the perfect matching is achieved between the fitted formula and calculated data.

As can be seen from Table 2, the contact force constant $Δ Q$ is negative for the dry contact. Here, the negative value implies that the there is no inner raceway contact force until the mutual approach exceeds a certain value. The reason might be due to the fact that the elastic deformation at the outer raceway contact resulting from the centrifugal inertia force on the ball element leads to a gap between the ball element and inner raceway. Therefore, the inner raceway comes into contact with the ball element resulting in the generation of contact force only if the mutual approach between raceways is large enough to eliminate the gap. For a larger inertia force on the ball element due to higher rolling speed, the gap becomes larger and a bigger mutual approach is required for the generation of the inner raceway contact force.

For the EHL contact, the combined effect of the lubricated film and the centrifugal inertia force determines the value of the contact force constant. On one hand, the lubricated film forms at the inner and outer raceways contacts at near to zero contact force due to rolling speed. On the other hand, the centrifugal inertia force results in the generation of the elastic deformation at the outer raceway contact and the gap at the inner raceway contact. For a high bearing speed, the lubricated film thickness is not enough to fill the gap, which is similar to the dry case and results in the negative contact force constant. For a low bearing speed, however, the hydrodynamic lift effect is dominant compared to the effect of the centrifugal inertia force. The inner raceway moves away from the outer raceway. In order to keep the mutual approach between raceways at zero value a positive load, i.e. contact force constant, should be applied to the inner raceway contact.

Fig. 2Contact force and mutual approach relation for both dry and EHL contacts between inner and outer raceways at two different rolling speeds

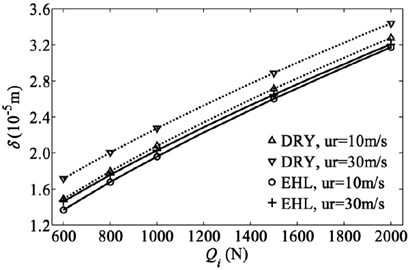
Table 2Related coefficients for inner raceway contact force and total mutual approach relation between inner and outer raceways at ball element position

Rolling speed (m/s)	$K$ (N/mⁿ)	$n$	$Δ Q$ (N)	Adjusted-R
10 (DRY)	1.078×10¹⁰	1.500	–19.214	1
30 (DRY)	1.180×10¹⁰	1.510	–155.465	1
10 (EHL)	8.562×10⁹	1.475	30.207	1
30 (EHL)	7.281×10⁹	1.457	–57.050	1

3. Bearing load-displacement relations considering EHL

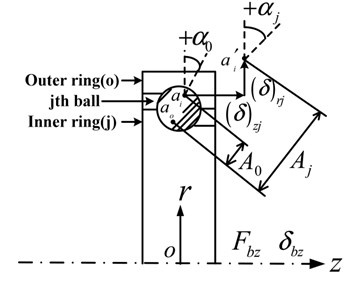
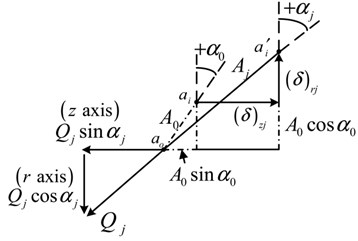
The schematic diagram for the relations between bearing loads and displacements for dry contact ball bearing are shown in Fig. 3 [21, 29]. As seen from Fig. 3(a), (b), for the ball bearing subjected to forces ( $F_{b x}$ , $F_{b y}$ , $F_{b z}$ ) and moments ( $M_{b x}$ , $M_{b y}$ ), the resultant translational and rotational displacements generated in the bearing inner are ( $δ_{b x}$ , $δ_{b y}$ , $δ_{b z}$ ) and ( $β_{b x}$ , $β_{b y}$ ), respectively. Also, the ball and raceways will be displaced. Detailed schematic diagram of the deformation at the $j$ th ball element position located at angle $ψ_{j}$ from the $x$ -axis is shown in Fig. 3(b). Here, $a_{o}$ is the position of the outer groove curvature centers, $a_{i}$ and $a_{i}^{'}$ are the initial and final locations of the inner raceway groove curvature center before and after the deformation at the $j$ th ball element position, respectively. The normal force $Q_{j}$ on the $j$ th ball element is given in detail in Fig. 3(c), where the bearing structures including ball element, inner raceway and outer raceway are ignored for purpose of simplification.

The bearing load-displacement relations for dry contact have been elaborated in [21, 28] and can be derived by considering the relations of (i) the displacements of inner ring and the deformation of outer raceway-ball element-inner raceway, (ii) the load and the deformation for outer raceway-ball element-inner raceway contact, and (iii) the normal loads on all ball elements and bearing forces and moments. The lubricated ball bearing load-displacement relations can be also derived on the basis of above steps, but the load and deformation relation for outer raceway-ball element-inner raceway for dry contact (denoted as (ii)) needs to be replaced with the lubricated contact force and mutual approach relation as shown in Eq. (11). The lubricated ball bearing load-displacement relations is given directly as follow and more detailed derivation process can be found in [21, 28]:

12

\{\begin{array}{l} F_{b x} \\ F_{b y} \\ F_{b z} \\ M_{b x} \\ M_{b y} \end{array}\} = \sum_{j = 1}^{N} \frac{K {δ_{j}}^{n} + Δ Q}{\sqrt{{[A_{0} s i n α_{0} + {(δ)}_{z j}]}^{2} + {[A_{0} c o s α_{0} + {(δ)}_{r j}]}^{2}}} \{\begin{matrix} [A_{0} c o s α_{0} + {(δ)}_{r j}] c o s ψ_{j} \\ [A_{0} c o s α_{0} + {(δ)}_{r j}] s i n ψ_{j} \\ [A_{0} s i n α_{0} + {(δ)}_{z j}] \\ r [A_{0} s i n α_{0} + {(δ)}_{z j}] s i n ψ_{j} \\ - r [A_{0} s i n α_{0} + {(δ)}_{z j}] c o s ψ_{j} \end{matrix}\},

where $α_{0}$ is the unloaded contact angle, and $α_{0}$ is zero for deep groove ball bearing. The mutual approach $δ_{j}$ at the $j$ th ball element position is calculated as:

13

δ_{j} = A_{j} - A_{0}, A_{j} = \sqrt{{[A_{0} s i n α_{0} + {(δ)}_{z j}]}^{2} + {[A_{0} c o s α_{0} + {(δ)}_{r j}]}^{2}},

{(δ)}_{r j} = δ_{b x} c o s (ψ_{j}) + δ_{b y} s i n (ψ_{j}) - r_{L}, {(δ)}_{z j} = δ_{b z} + r [β_{b x} s i n (ψ_{j}) - β_{b y} c o s (ψ_{j})],

where $A_{0}$ and $A_{j}$ are the unloaded and loaded relative distance between the inner and outer raceway groove curvature centers. ${(δ)}_{r j}$ and ${(δ)}_{z j}$ are the radial and axial displacements at the $j$ th ball element position, respectively. $r_{L}$ is the radial clearance, and $r$ is the radial distance of inner raceway groove curvature center for the ball bearing.

Fig. 3Ball element bearing kinematics and co-ordinate system

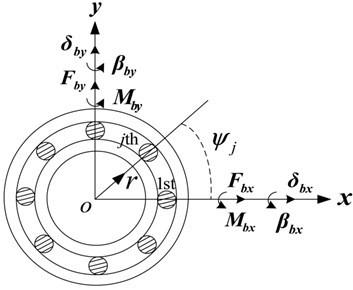
a)

b)

c)

4. Development of bearing stiffness matrix

The stiffness matrix for the ball bearing can be derived from the partial derivatives of the load expressions (i.e., Eq. (13)) with respect to the displacements (including both translational and rotational displacements) of the inner ring [21], which is given as:

14

{[K]}_{b} = [\begin{array}{l} \frac{\partial F_{b i}}{\partial δ_{j}} & \frac{\partial F_{b i}}{\partial β_{j}} \\ \frac{\partial M_{b i}}{\partial δ_{j}} & \frac{\partial M_{b i}}{\partial β_{j}} \end{array}] = [\begin{array}{l} K_{b x x} & K_{b x y} & K_{b x z} & K_{b x θ_{x}} & K_{b x θ_{y}} \\ K_{b y x} & K_{b y y} & K_{b y z} & K_{b y θ_{x}} & K_{b y θ_{y}} \\ K_{b z x} & K_{b z y} & K_{b z z} & K_{b z θ_{x}} & K_{b z θ_{y}} \\ K_{b θ_{x} x} & K_{b θ_{x} y} & K_{b θ_{x} z} & K_{b θ_{x} θ_{x}} & K_{b θ_{x} θ_{y}} \\ K_{b θ_{y} x} & K_{b θ_{y} y} & K_{b θ_{y} z} & K_{b θ_{y} θ_{x}} & K_{b θ_{y} θ_{y}} \end{array}] .

Note the above ball bearing stiffness matrix consists of radial, axial and rational stiffness coefficients (diagonal) and coupling stiffness coefficient (off-diagonal). The explicit expression of each item in ${[K]}_{b}$ is the function of bearing displacements as shown in Appendix A (note that ${[K]}_{b}$ is symmetric, i.e. $K_{b i j} = K_{b j i}$ ). It should be noted that all stiffness terms associated with the torsional degree of freedom $β_{b z}$ are zero (having been omitted) due to the fact that an ideal bearing allows free rotation about the $z$ -direction.

Since the bearing stiffness coefficients are the function of bearing displacements, the stiffness matrix can be directly determined for a given a set of bearing displacements input. Yet, in practice, only the external forces applied to a bearing system are known. In such cases, the resultant bearing displacement vectors due to known bearing forces can be obtained by solving the system of nonlinear algebraic equations describing the load-displacement relation of the bearing system as shown in Eq. (12). For the solution to be reliable, an appropriate numerical method must be chosen to solve these nonlinear equations iteratively. Energy method is proposed to solve the dry contact bearing displacements and proved to be a fast and reliable numerical method for the computation of bearing displacements in [28]. The proposed energy method is based on the principle of minimum potential energy derived from classical mechanics, which is a global searching method. The exact displacements can be found by searching for the displacements that yield the minimum total potential energy of the bearing system. This algorithm overcomes the deficiencies seen in classical iterative method requiring the trial-and-error of different initial estimates.

However, in the current analysis, the energy method cannot be used directly to solve lubricated bearing displacement due to the existence of lubrication film. Since the lubrication film thickness is much less than the elastic deformation at contact domain, the differences of bearing displacements for dry contact and lubricated contact are very subtle. The dry contact bearing displacements should be a good initial guesses for lubricated bearing displacements. Therefore, the energy method is applied first to solve the dry contact bearing displacements; then these displacements as the initial guesses of lubricated bearing displacements are substituted into classic iterative method, such as Newton-Raphson, to solve the exact lubricated bearing displacements. Finally, the stiffness matrix of the ball bearing is calculated by the obtained bearing displacements.

5. Influence of EHL on the bearing stiffness

The stiffness coefficients of lubricated deep groove ball bearing subjected to following load conditions are investigated: (i) radial load and (ii) the combination of radial load, axial load and moment. For the purpose of comparison, the dry contact bearing stiffness coefficients are also given in current analysis.

5.1. Bearing stiffness due to radial load

Given the radial load applied on the bearing, the bearing inner ring generate only the translation in the radial plane (bearing plane), in such case only the stiffness coefficients in the radial plane should be concerned. For a symmetry reference position, the applied radial load $F_{b x}$ towards the first ball element is shown in Fig. 4. The radial displacement $δ_{b x}$ and the stiffness coefficients $K_{b x x}$ , $K_{b y y}$ exist, and other displacements and stiffness coefficients in radial plane are zero.

Fig. 5 and Fig. 6 show the non-zero displacements and stiffness coefficients for different rolling speeds and contact conditions, respectively, as a function of the radial loads of bearing. The radial displacements $δ_{b x}$ for both dry and lubricated contacts increase as the radial load increases. It is noticed that for the radial load level of 2000 N, the radial displacements for the dry contact are about 5 % ( $u r =$ 10m/s) and 10 % ( $u r =$ 30 m/s) more than those for the lubricated contact. But this discrepancy reduces to 3.2 % ( $u r =$ 10 m/s) and 6.8 % ( $u r =$ 30 m/s) when the radial load is increased to 4000 N. The trend indicates that the effect of EHL on the bearing displacement decreases gradually with the increasing of radial load. That is reasonable since the increased load tends to squeeze the lubrication and the film thickness becomes smaller. In particular, as can be seen from Fig. 6, the EHL has a minimum influence on radial stiffness coefficients. No matter for rolling speed of 10 m/s or 30 m/s, the radial stiffness coefficient $K_{b x x}$ and $K_{b y y}$ for lubricated contact are 1 % less than those for the dry contact throughout the whole range of radial load from 2000 N to 4000 N. The comparison has fully demonstrated that the effect of EHL on the radial stiffness coefficients can be ignored when only the radial load is applied on the deep groove ball bearing. Due to the cage motion, the stiffness coefficients have a time varying characteristic as shown in [10]. However, for other orbital positions of ball elements except for symmetry position in Fig. 4, the difference of the radial stiffness coefficients of bearing under the dry and lubricated contact conditions is still negligible. Therefore, these results are not presented in current analysis.

Fig. 4Representation of the symmetric position of radial loaded deep groove ball bearing

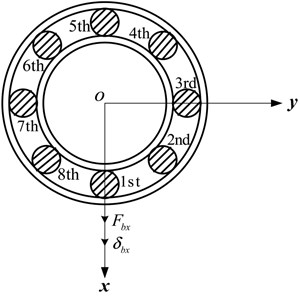
Fig. 5Variation of radial displacement of bearing with radial load

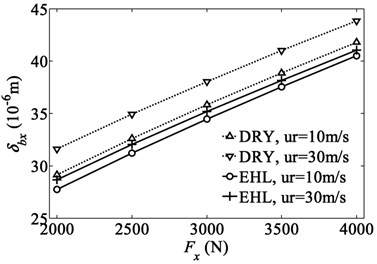
Fig. 6Variation of radial stiffness coefficients of bearing with radial load

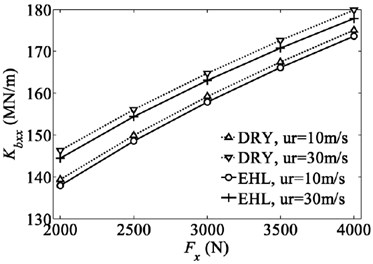
a)

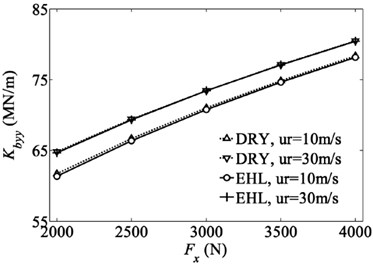
b)

5.2. Bearing stiffness due to the combination of loads

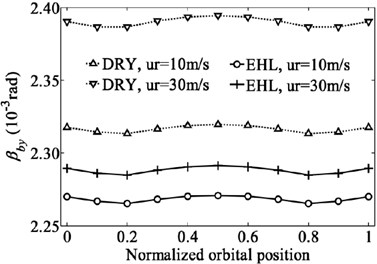
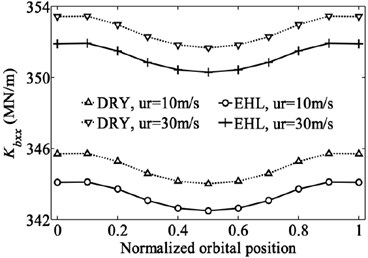
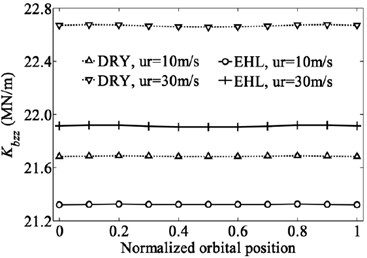
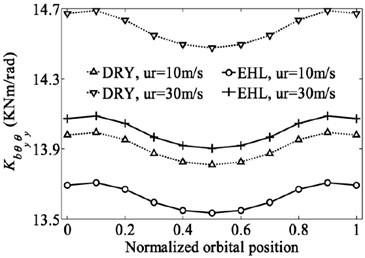
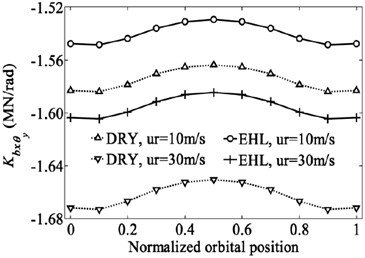
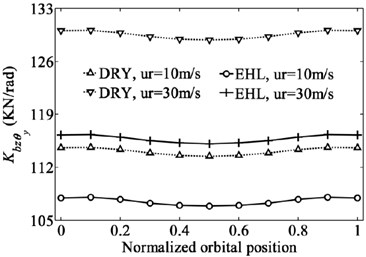
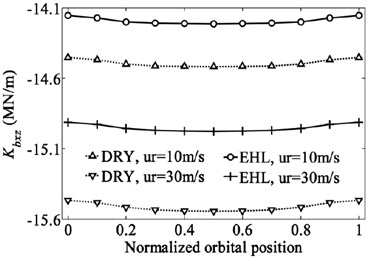
Although the deep groove ball bearing is designed mainly to support the radial load, the combination of loads including radial load, axial load and moment is often applied to deep groove ball bearing due to the bending motion on the shaft. The bearing inner ring generates not only in-plane type motion but also out-of-plane type motion. In such case the radial, axial, rotational and some coupling stiffness coefficients are all non-negligible [29]. Therefore, the effect of EHL on the dominant stiffness coefficients of a deep groove ball bearing subjected to the combination of loads ( $F_{x} =$ 2000 N, $F_{z} =$ 1500 N and $M_{y} =$ 4000 Nmm) are investigated here. The variation of the displacements and dominant stiffness coefficients of bearing with normalized orbital position angle are shown in Fig. 7 and Fig. 8. The normalized orbital position angle is defined as $ψ_{1} / ψ_{N}$ where $ψ_{1}$ is the angular distance between 1st ball element and $x$ -axis and $ψ_{N} = 2 π / N$ radians is the element-to-element angular distance.

As can be seen from Fig. 7, the results clearly show the periodic nature of the stiffness coefficients with the normalized orbital position angle except those coefficients related to translational degree of freedom of z direction keeping almost horizontal. The periodic nature of the stiffness coefficients implies that the ability of bearing to resist the deformation varies with the positions of rolling elements, which results in the periodic fluctuation of bearing displacements. The time varying stiffness characteristic of bearing has been considered as one of the major noise and vibration sources in the rotating machineries typically seen in automotive, aerospace and industrial applications.

Fig. 7Variation of bearing displacements with dimensionless orbital position angle

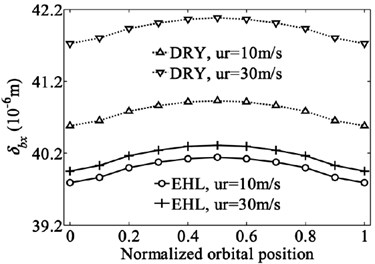
a)

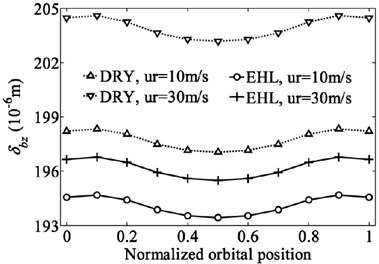
b)

c)

As expected, the lubricated bearing displacements are less than the dry contact bearing displacements due to the existence of lubrication film. The differences of the displacements for the two contact conditions increase with the bearing speed. The comparison of the stiffness coefficients also shows the similar tendency. For the same speed, the stiffness coefficients for lubricated bearing are less than those for dry contact bearing (absolute value is compared for negative stiffness coefficients). But the difference of each stiffness coefficient for the two contact conditions is distinctively different. For the rolling speed of 30 m/s, the radial and axial stiffness coefficients of the bearing for dry contact are only 1.5 % and 3.5 % greater than those for lubricated bearing, respectively. However, the rational and coupling stiffness coefficients for dry contact are 4 % to 11 % greater than those for lubrication contact. The EHL has a more remarkable effect on the rotational and coupling stiffness coefficients compared to the effect of EHL on the radial and axial stiffness coefficients, and this trend is more obvious with the increasing of rolling speed (or bearing speed). In addition, multiple different values of the combination of loads are tested to analyze the effect of lubrication on the bearing stiffness. Nearly the same conclusions can be obtained that the rotational and coupling stiffness coefficients of the bearing for the lubricated contact are much lower than those for the dry contact, but the differences for the radial and axial coefficients under the two contact conditions are weak.

Fig. 8Variation of bearing stiffness coefficients with dimensionless orbital position angle

a)

b)

c)

d)

e)

f)

According to Lim’s work [30], the dynamic model of the shaft-bearing-plate-mount system including the rational and coupling stiffness coefficients of bearing is indeed capable of predicting plate rigid-body angular motion or plate flexural motion as excited by shaft motion. The predicted results also show good agreement with those observed in the experiment. But the vibration model ignoring the rational and coupling stiffness coefficients cannot reach this goal. This showed that the rotational and coupling stiffness coefficients are the key factors demonstrating accurately the vibration behaviors of the shaft-bearing-plate-mount system. Due to the remarkable effect of EHL on the rotational and coupling stiffness coefficients, especially for high bearing speed, the EHL contact behavior has to been considered in the analysis of vibration behavior of the shaft-bearing-plate-mount system.

6. Conclusions

Based on the lubricated contact relation between raceways, the effect of EHL on the stiffness coefficients of deep groove ball bearing was analyzed. The power form formulation was used to capture successfully the trend of the mutual approach with the contact force for the lubricated inner raceway-ball element-outer raceway contact, and the effect of the centrifugal inertial force was also considered. The load-displacement relation for lubricated bearing was established, and the stiffness matrix with five dimensions was derived by evaluating the partial derivatives of the bearing loads with respect to each bearing displacement term.

The radial load and the combination of loads including radial, axial and moment loads as two forms of external loads are applied on the deep groove ball bearing. The dominant stiffness coefficients under the lubricated and dry contact conditions were calculated and compared. The comparison showed that the effect of EHL on the radial stiffness coefficients of bearing subjected to only radial load is negligible. EHL has a weak influence on radial and axial stiffness coefficients but a significant effect on the rotational and coupling stiffness coefficients when the combination of loads consisting of radial, axial and moment loads are applied on the bearing. In the future work, this enhanced bearing stiffness matrix considering the EHL effect will be applied for the dynamic analysis of geared rotor-bearing systems.

References

Peng T. Coupled Multi-Body Dynamic and Vibration Analysis of Hypoid and Bevel Geared Rotor System. Ph.D. Thesis, University of Cincinnati, Cincinnati, 2011.

Search CrossRef
Yang J. Nonlinear Dynamics of Driveline Systems with Hypoid Gear Pair. Ph.D. Thesis, University of Cincinnati, Cincinnati, 2012.

Search CrossRef
He S., Gunda R., Singh R. Effect of sliding friction on the dynamics of spur gear pair with realistic time-varying stiffness. Journal of Sound and Vibration, Vol. 301, Issue 3, 2007, p. 927-949.

Publisher
Jones A. B. A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions. Journal of Basic Engineering, Vol. 82, Issue 2, 1960, p. 309-320.

Publisher
Shimizu H., Tamura H. Vibration of Rotor Based on Ball Bearing. 1st Report, Bulletin of JSME, Vol. 9, 1966.

Publisher
Tamura H., Shimizu H. Vibration of Rotor Based on Ball Bearing. 2nd Report, Bulletin of JSME, Vol. 10, 1967.

Publisher
Peng T., Lim T. C. Dynamics of hypoid gears with emphasis on effect of shaft rotation on vibratory response. ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2007.

Publisher
Peng T., Lim T. C. Influence of gyroscopic effect on hypoid and bevel geared system dynamics. SAE International Journal of Passenger Cars-Mechanical Systems, Vol. 2, Issue 1, 2009, p. 1377-1386.

Publisher
He S., Singh R., Pavic G. Effect of sliding friction on gear noise based on a refined vibro-acoustic formulation. Noise Control Engineering Journal, Vol. 56, Issue 3, 2008, p. 164-175.

Publisher
Nonato F., Cavalca K. L. An approach for including the stiffness and damping of elastohydrodynamics point contacts in deep groove ball bearing equilibrium models. Journal of Sound and Vibration, Vol. 333, Issue 25, 2014, p. 6960-6978.

Publisher
Wijnant Y. H. Contact Dynamics in the Field of Elastohydrodynamic Lubrication. Ph.D. Thesis, University of Twente, The Netherlands, 1998.

Publisher
Wensing J. On the Dynamics of Ball Bearings. Ph.D. Thesis, University of Twente, The Netherlands, 1998.

Search CrossRef
Wijnant Y. H., Wensing J. A., Van Nijen G. C. The influence of lubrication on the dynamic behaviour of ball bearings. Journal of Sound and Vibration, Vol. 222, Issue 4, 1999, p. 579-596.

Publisher
Wiegert B., Hetzler H., Seemann W. A simplified elastohydrodynamic contact model capturing the nonlinear vibration behavior. Tribology International, Vol. 59, Issue 2, 2013, p. 79-89.

Publisher
Zhang Y. Y., Liu H. J., Zhu C. C., Liu M. Y., Song C. S. Oil film stiffness and damping in an elastohydrodynamic lubrication line contact-vibration. Journal of Mechanical Science and Technology, Vol. 30, Issue 7, 2016, p. 3031-3039.

Publisher
Nonato F., Cavalca K. L. On the non-linear dynamic behavior of elastohydrodynamic lubricated point contact. Journal of Sound and Vibration, Vol. 329, Issue 22, 2010, p. 4656-4671.

Publisher
Jacobs W., Boonen R., Sas P., Moens D. The influence of the lubricant film on the stiffness and damping characteristics of a deep groove ball bearing. Mechanical Systems and Signal Processing, Vol. 42, Issues 1-2, 2014, p. 335-350.

Publisher
Rahnejat H., Gohar R. The vibrations of radial ball bearings. Proceedings of the Institution of Mechanical Engineers, Part C, Journal of Mechanical Engineering Science, Vol. 199, Issue 3, 1985, p. 181-193.

Publisher
Liu J., Shao Y. M., Zuo M. J. The effects of the shape of localized defect in ball bearings on the vibration waveform. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-Body Dynamics, Vol. 227, Issue 3, 2013, p. 261-274.

Publisher
Liu J., Shao Y. M. Vibration modelling of nonuniform surface waviness in a lubricated roller bearing. Journal of Vibration and Control, 2015.

Publisher
Babu C. K., Tandon N., Pandey R. K. Nonlinear vibration analysis of an elastic rotor supported on angular contact ball bearings considering six degrees of freedom and waviness on balls and races. Journal of Vibration and Acoustics, Vol. 136, Issue 4, 2014, p. 044503.

Publisher
Lim T. C., Singh R. Vibration transmission through rolling element bearings. Part 1: bearing stiffness formulation. Journal of Sound and Vibration, Vol. 139, Issue 2, 1990, p. 179-199.

Publisher
Venner C. H., Lubrecht A. A. Multilevel methods in lubrication. Tribology Series, Vol. 37, 2000, p. 1-379.

Search CrossRef
Harris T. A., Kotzalas M. N. Rolling Bearing Analysis. Essential Concepts of Bearing Technology. 5th Edition, CRC Press, 2006.

Publisher
Jan C. A non-symmetric discretization formula for the numerical solution of elastohydrodynamic lubrication circular contact problem. Tribology International, Vol. 31, Issue 12, 1998, p. 761-765.

Publisher
Roelands C. J. A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricanting Oils. Ph.D. Thesis, Delft University of Technology, The Netherlands, 1966.

Search CrossRef
Dowson D., Higginson G. R. Elastohydrodynamic Lubrication: Fundamentals of Roller and Gear Lubrication. Pergamon Press, Oxford, 1966.

Search CrossRef
Liu S. B., Wang Q., Liu G. A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear, Vol. 243, Issues 1-2, 2000, p. 101-111.

Publisher
Zhang Y., Sun G. H., Lim T. C., Xie L. Y. A fast and reliable numerical method for analyzing loaded rolling element bearing displacements and stiffness. Journal of Vibroengineering, Vol. 17, Issue 2, 2015, p. 620-642.

Search CrossRef
Lim T. C., Singh R. Vibration transmission through rolling element bearings. Part 2: system studies. Journal of Sound and Vibration, Vol. 139, Issue 2, 1990, p. 201-225.

Publisher

Cited by

Comparative analysis of angular contact bearing stiffness calculated by Hertz contact and thermo-elastohydrodynamic lubrication

(2024)

Vibration Engineering and Technology of Machinery, Volume I

Sameera Mufazzal | S. M. Muzakkir | Sidra Khanam

(2023)

Advances in Mechanical Engineering

Sameera Mufazzal | S. M. Muzakkir | Sidra Khanam

(2021)

Time-varying stiffness characteristics of roller bearing influenced by thermal behavior due to surface frictions and different lubricant oil temperatures

Xu Hao | Jingyu Zhai | Junshuai Liang | Yitong Chen | Qingkai Han

(2020)

An improved stiffness model for line contact elastohydrodynamic lubrication and its application in gear pairs

Jiaxing Pei | Xu Han | Yourui Tao

(2020)

Study of sealing mechanism of gas-liquid miscible backflow pumping seal

Shicong Li | Caifu Qian | Shuangxi Li | Qingzhan Li | Haoran Liao

(2020)

About this article

Received

21 March 2016

Accepted

12 August 2016

Published

15 November 2016

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2016.17002

Keywords

elastohydrodynamic lubrication (EHL)

deep groove ball bearing

mutual approach

centrifugal inertial force

coupling stiffness coefficient

Acknowledgements

The authors are grateful for the financial support provided by the Natural Science Foundation of China (Grant No. 51335003) and the program for Innovative Research Team in University of Ministry of Education of China (1RT1160).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 04 02

Optimization of lubrication characteristics of wind turbine’s transmission system based on Newton Raphson method

Li Cao, Wenlei Sun, Tao Gou

Research article

2020 11 21

Vibration analysis of three-DOF motor with liquid suspension based on fluid-solid coupling

Zheng Li, Feihong Yue

Research article

2020 10 19

An improved mesh stiffness calculation model of spur gear pair under mixed EHL friction with spalling effect

Siyu Wang, Rupeng Zhu

Research article

2018 04 20

Influence of oil film stiffness on natural characteristics of single-rotor three-input helicopter main gearbox

Yuan Chen, Ru Peng Zhu, Zai Chun Feng, Guang Hu Jin, Wei Zhang

Y. Zhang, L. Xie, X. Lv, and G. Sun, “The influence of elastohydrodynamic lubrication on the stiffness of deep groove ball bearing,” Journal of Vibroengineering, Vol. 18, No. 7, pp. 4178–4192, Nov. 2016, https://doi.org/10.21595/jve.2016.17002

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.17002
UR  - https://doi.org/10.21595/jve.2016.17002
TI  - The influence of elastohydrodynamic lubrication on the stiffness of deep groove ball bearing
T2  - Journal of Vibroengineering
AU  - Zhang, Yu
AU  - Xie, Liyang
AU  - Lv, Xiao
AU  - Sun, Guohua
PY  - 2016
DA  - 2016/11/15
PB  - JVE International Ltd.
SP  - 4178-4192
IS  - 7
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Zhang_2016,
	doi = {10.21595/jve.2016.17002},
	url = {https://doi.org/10.21595/jve.2016.17002},
	year = 2016,
	month = {nov},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {7},
	pages = {4178--4192},
	author = {Yu Zhang and Liyang Xie and Xiao Lv and Guohua Sun},
	title = {The influence of elastohydrodynamic lubrication on the stiffness of deep groove ball bearing},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]Y. Zhang, L. Xie, X. Lv, and G. Sun, “The influence of elastohydrodynamic lubrication on the stiffness of deep groove ball bearing,” Journal of Vibroengineering, vol. 18, no. 7, pp. 4178–4192, Nov. 2016, doi: 10.21595/jve.2016.17002.

Copy IEEE

Copied to clipboard!

Zhang, Yu, Liyang Xie, Xiao Lv, and Guohua Sun. “The Influence of Elastohydrodynamic Lubrication on the Stiffness of Deep Groove Ball Bearing.” Journal of Vibroengineering 18, no. 7 (November 15, 2016): 4178–92. https://doi.org/10.21595/jve.2016.17002.

Copy Chicago

Copied to clipboard!

The influence of elastohydrodynamic lubrication on the stiffness of deep groove ball bearing

Abstract

1. Introduction

2. EHL contact model

2.1. Definition of mutual approach

2.2. Contact force and mutual approach relationship

3. Bearing load-displacement relations considering EHL

4. Development of bearing stiffness matrix

5. Influence of EHL on the bearing stiffness

5.1. Bearing stiffness due to radial load

5.2. Bearing stiffness due to the combination of loads

6. Conclusions

References

Cited by

About this article

Related Articles