Abstract
The lubricant film of hydrostatic circular pad in the heavy-duty rotary table is affected by the roughness, thermal and hydrodynamic effect, which can cut down the load-carrying capacity and machining accuracy of the heavy-duty machine tool. In this paper, a coupled energy equation with mean Reynolds equation based on the Christensen’s stochastic model of rough surfaces is presented to analyze the temperature rising, pressure distribution and load-carrying capacity of the hydrostatic circular pad. The mean Reynolds equation, momentum equation, continuity equation, and energy equation are coupled and solved using the finite difference method to obtain the characteristics of lubricant film. It is found that the uneven pressure distribution and the temperature rising of lubricant film in resistive oil edge of hydrostatic circular pad are related to the increase of dimensionless hydrodynamic parameter S due to the thermal and hydrodynamic coupling effect. The load-carrying capacity and stability of heavy-duty rotary table is weakened due to the thermal and hydrodynamic effects.
1. Introduction
Due to the high load-carrying capacity, small viscous dissipation, high stiffness, low running friction, long service life, and good resistance to vibration, the heavy-duty hydrostatic rotary table has been widely used to carry and machine the large workpiece in the heavy-duty machine tool. Hydrostatic circular pads form a part of the heavy-duty hydrostatic rotary table with quantitative oil supply system to support the workpiece. The basic design of hydrostatic rotary table was conducted by Fuller [1], Rippel [2] and Rowe [3]. Numerous studies on hydrostatic rotary table or bearing can be found in literature, where the researchers have paid attention to the various aspects of the characteristics of hydrostatic rotary or bearing. Important aspects that determine the performance of a hydrostatic circular pad are the flow pattern, rough surface of resistive oil edge, heat generation as well as the hydrodynamic effect.
The surfaces of resistive oil edge are all rough in engineering practice to reflect the processes that have been used in forming and finishing stages. Moreover, the height of the roughness is generally of the same order as the mean asperities in a lubricated contact. Under these situations, the influence of surface roughness on the characteristics of hydrostatic circular pads should be considered. Patir and Cheng [4, 5] developed an average flow model of a randomly generated rough surface with known statistical properties over the surface area. While using stochastic concept, a film averaging concept for striated roughness was introduced by Christensen [6, 7]. Elrod [8] and Tonder [9] also confirmed this approach. Surface roughness could affect the dynamic stiffness and damping characteristics of compensated hydrostatic thrust bearings.
Beside the roughness of surface, the flow pattern of lubricant film can also be changed by the relative movement of surface. With the improvement of speed, the hydrodynamic effect or the centripetal inertia become more and more important for the hydrostatic support system, which should not be ignored. Osterle and Hughes [10] and Dowson [11] analyzed the inertia effects in hydrostatic thrust bearings using the assumptions of the classical lubrication theory where they assumed that the term associated with the centripetal inertia cannot be neglected. Thus, they have created a model that retains lumped centripetal inertia effects. Using these assumptions, Chow [12] modeled an annular recess hydrostatic thrust bearing and Dowson [13] considered inertia effects on in parallel circular bearings.
The temperature rising of oil film is an important factor on affecting the carrying capacity of hydrostatic system for the heavy-duty rotary table. Bouyer [14] combined the Reynolds equation with energy equation to make a thermo-elastohydrodynamic analysis on a plain journal bearing with a single groove under steady load. And the bearing deformation was also taken into account. Several experimental tests were performed by Serrato [15] in NU205 roller bearings, lubricated with mineral oil of three different viscosity grades (ISO 10, 32 and 68). It proved the higher the oil viscosity, the higher the temperature of the oil film in the high frequency of work condition. The change of viscosity has a great influence on oil film thickness and mechanical vibration. Wang [16] numerically simulated the bearing lubricating film, and obtained the temperature distribution in the bearing with dynamic pressure oil film and analyzed the influence of the three dimensional temperature field on the practical lubrication performance of the bearing under a given load. The temperature changes in the oil of a hydrostatic bearing would cause the changes of the viscosity and the density.
However, the oil film of hydrostatic system is indeed affected by multi-factor coupling effect. Kapur and Kamlesh [17] discussed the effects of inertia and temperature on the performance of a hydrostatic thrust bearing. The expressions for pressure profile and load-carrying capacity were obtained under conditions of adiabatic flow. The numerical results for pressure distribution were obtained at different step positions and film thickness ratios for several values of thermal conductivity. Lin [18] analyzed the thermal and cavitation effect on the journal bearing system. A comparison with the published experimental results was presented and discussed, and theoretical predictions agreed well with the experimental results. Sinha and Getachew [19] analyses the thermal and roughness effects on different characteristics of finite rough tilted pad slider bearings. Two models of one-dimensional roughness, longitudinal and transverse are considered, the modified Reynolds equation, momentum equation, continuity equation and energy equation are coupled and solved using the finite difference method to yield various bearing characteristics.
In this paper, the roughness, hydrodynamic and thermal coupled effect on the pressure distribution and load-carrying capacity of circular oil pad is analyzed based on the Christensen’s stochastic model of rough surfaces. The viscosity and density of lubricant film is assumed to depend on the temperature for presented coupling model. The mean Reynolds equation, momentum equation, continuity equation, and energy equation are coupled and solved using a finite difference method to obtain the characteristics of lubricant film. The hydrodynamic and thermal effect rule of circular oil pad for the hydrostatic rotary table can be obtained, which will provide theoretical foundation for optimization of heavy-duty hydrostatic rotary table.
2. Background
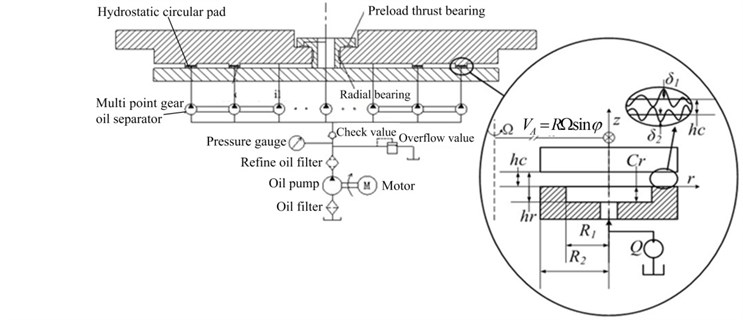
The support system of heavy-duty rotary table is composed of hydrostatic circular pads, preload thrust bearing, and radial bearing, as shown in Fig. 1. The heavy-duty rotary table can bear the axial load by the coordinated application of hydrostatic circular pads and preload bearing, which can make the rotary table keeping a high stiffness in light load. The main role of radial bearing is to overcome the influence of the centrifugal force due to the existence of the offset load. The constant flow supply system is used to provide the lubricant oil for all of those hydrostatic pads and bearings in the heavy-duty rotary table. The diameter of heavy-duty rotary table is 10 m. The 24 hydrostatic circular pads are evenly distributed in the two circle rails, in which the diameter of inner circle rail is 3.4 m with 8 hydrostatic circular pads and that of outside rail is 6.8 m with 16 hydrostatic circular pads. The rated load-carrying capacity of hydrostatic rotary table is 400 T. The maximum diameter of machined work piece is 9.5 m. The maximum rotate speed of heavy-duty rotary table is 30 rpm.
The hydrostatic circular pad is one of the most important parts, whose characteristic can determinate the load-carrying capacity and machine accuracy of heavy-duty rotary table. Especially for the hydrostatic circular pads in outer circular rail, the thermal and hydrodynamic effect is more obvious comparing with those in inner circular rail. Therefore, the hydrostatic circular pads of outer circular rail are chosen as the study object in this paper. However, the same analysis method is suitable for hydrostatic circular pads in the inner circular rail. The only difference is the boundary condition of hydrostatic circular pads.
Fig. 1 shows a hydrostatic circular pad in outside circular rail. The lubricant oil enter the oil chamber by the inlet hole with a constant lubricant flow rate , then the hydrostatic effect is formed to support the heavy-duty rotary table. The film thickness of recess is . The depth of the recess is , depicts the film thickness of resistive oil edge. The inner radius and outer radius of the hydrostatic circular pad is and , respectively. The abrupt change of lubricant film thickness around can be considered as the “Rayleigh steps” (Ting, 1971). The lubricant leaks away through the clearances on the land areas. The pressure around is atmospheric pressure, which can be deemed as 0 MPa. Due to the tangential effect of lubricant film during the process of rotation for the heavy-duty rotary table, we can define the line speed of hydrostatic circular pad in tangential direction with . is the angular velocity of heavy-duty rotary table. depicts the radius of outer rail of heavy-duty rotary table. is the angle between angular velocity of rotary table and radial direction in center of hydrostatic circular pad. Comparing with inertial effect of traditional hydrostatic trust bearing [4], the rotating center of heavy-duty rotary table is offset the center of hydrostatic circular pad. The hydrodynamic effect of hydrostatic circular pad is difficult to be accurately described by adapting the above mentioned method. In addition, the friction will cause the temperature rising and viscosity decreasing of lubricant film during the process of rotation, which can affect the load-carrying capacity and machine accuracy of heavy-duty rotary table.
Fig. 1Schematic diagram of heavy hydrostatic rotary table and hydrostatic circular pad
3. The mean Reynolds equation based on the Christensen’s stochastic model of rough surfaces
The lubricant oil in the hydrostatic circular pad is assumed to be incompressible and viscous. Since the geometry of the hydrostatic pad is a circular shape, modeling of the fluid flow in the hydrostatic circular pad should be in cylindrical coordinates. Since the height of lubricant film is extra-thin comparing with the radius of rotary table, , we assume that the lubricant film pressure is constant in the direction, which can be written as 0. In addition, the flow velocity in the direction is much less than flow velocities and in the and directions. Therefore, the velocity gradient of lubricant film can be ignored besides , , and . Then the Navier-Stokes equation can be simplified as [18]:
Integrating Eq. (2) with respect to with the boundary conditions at the surfaces of the circular pad: 0, , . The radial flow velocity can be obtained as:
And the flow rate of hydrostatic circular pad can be calculated by integrating Eq. (4):
Substituting Eq. (4) into Eq. (1) and integrating it with the boundary conditions: 0, , , then the Reynolds equation of hydrostatic circular pad is derived as:
The geometry of the local lubricant film is made up two parts [15]:
where, denotes the random part resulting from the surface roughness asperities measured from the nominal mean level, describes a random variable which characterizes the definite roughness arrangement, and represents the nominal smooth part of the film geometry. In order to set up a foundation for the application of stochastic theory, the assumptions presented by Christensen [6, 7] are introduced. We can obtain the equations considering the two type roughness model by calculating the expected values on both sides of the Eq. (6). The Reynolds-type equation with radial one-dimensional roughness is described by:
and the Reynolds-type equation with circumferential one-dimensional roughness is defined as:
where, represents the average static pressure oil film. is the expectancy operator defined by:
and is the probability density distribution for the stochastic variables, which obey the Gaussian distribution. The polynomial form is chosen to simulate the Gaussian distribution as:
where, is a random variable for half of oil film thickness, which can be defined as , describes the standard deviation. The following equations can be obtained:
where, is the variance of roughness distribution with .
Assuming:
and:
Hence, the mean Reynolds equations and flow rate equation of hydrostatic circular pad can be rewritten, respectively, as:
In order to obtain the pressure distribution of hydrostatic circular pad, the boundary conditions of oil chamber and resistive oil edge can be reset. For the boundary conditions of oil chamber (), we assume , , , and the boundary conditions of resistive oil edge () are defined as , , , . However, the mean Reynolds equations is derived based on the isoviscous hypothesis, which is contradicted with the viscosity changes of lubricant film due to the temperature rising during the running process of heavy rotary table. Therefore, we define the viscosity as the average density across the lubricant film. Substituting the following boundary conditions into Eq. (15) and (16):
The pressure distribution of resistive oil edge for hydrostatic circular pad can be obtained as:
By integrating the pressure distribution, we can obtain the load-carrying capacity of hydrostatic circular pad as:
According to Roberto Bassani’s analysis, two assumption conditions are introduced in this paper. The simplified energy equation can be written as:
Due to the viscosity and density of lubricant film is related to temperature , the viscosity-temperature equation and density-temperature equation can be obtained as:
4. Nondimensionalization and solution of equations
4.1. The nondimensionalization of equations
It is necessary to nondimensionalizate the Reynolds equation and energy equation, in which the dimensionless constants that govern the fluid flow and the temperature distribution become clear. Meanwhile, it offers better understanding in the underlying physics of the lubrication of the hydrostatic circular pad [19]. The following dimensionless variables are introduced for the dimensionless Reynolds equation and energy equation:
where, is a dimensionless hydrodynamic parameter. Substituting the dimensionless parameters into Eqs. (18-22), the non-dimensionalization of equations can be obtained. The dimensionless pressure distribution equation of lubricant film can be written as:
The dimensionless load-carrying capacity equation is:
The dimensionless energy equation, viscosity-temperature equation and density-temperature equation can be indicated respectively as:
4.2. Treatment of the solution
In order to solve the pressure distribution of hydrostatic circular pad, the finite difference method is introduced to discretize and solve Reynolds equations with radial and circumferential roughness. Two cases are considered:
Case 1: 0, solving the Reynolds Eq. (23) to obtain the hydrostatic value, which satisfies the general solution of the homogeneous mean Reynolds equations. The pressure of recess is assumed to be the same one with that of inlet, which means the dimensionless variable 1. For this case, the pressure distribution of recess is unnecessary to be considered and we only solve the pressure distribution of resistive oil edge. As the resistance of recess is much less than that of resistive oil edge, we can assume that the pressure gradient is zero in the radial direction.
Case 2: , 0, solving the Reynolds Eq. (23) to obtain the hydrodynamic value, which satisfies the special solution of non-homogeneous mean Reynolds equations. Considering the hydrodynamic pressure of lubricant film is caused by the hydrodynamic effect, we may assume the pressure of recess and resistive oil edge are all zero. For this case, we can compute the pressure of recess and resistive oil edge. Due to the mean Reynolds equations are linear partial differential equations, the hydrodynamic value can be linearly added with that of hydrostatic effect for the circular pad.
The boundary conditions are critical for the mathematical model to reflect the operation states of hydrostatic circular pad. Since the steady state operating conditions is only considered for the circular pad, the cavitation effect is ignored in this study. Therefore, the velocity and pressure boundary conditions are introduced to solve the Reynolds equations. To ensure the convergence and consistency, the convergence factor is set as 10-5.
5. Results and discussion
The study is mainly concerned with the combined roughness, hydrodynamic and thermal effect on the steady-state performance of hydrostatic circular pad for the heavy-duty rotary table. The parameters of hydrostatic circular pads are shown in Table 1.
Table 1The parameters of hydrostatic circular pads
Parameter name | Parameter values | Parameter name | Parameter values |
Ambient density () | 900 kg/m3 | Temperature coefficient in viscosity formula () | 0.035/K |
Initial temperature of lubricant oil () | 310K | Inner rail radius () | 160 mm |
Mean steady nominal film thickness () | 0.1 mm | Outer rail radius () | 175 mm |
Specific heat of lubricant film () | 1926 J/(kg·K) | Film thickness of resistive oil edge () | 0.1 mm |
Ambient viscosity () | 0.1 Pa·s | Film thickness of oil chamber () | 3 mm |
Mechanical equivalent of heat () | 0.132 | Thermal conductivity of the lubricant film (K) | 0.145 w/(m·k) |
Temperature coefficient in density formula () | 0.00064737 |
In order to reflect the hydrodynamic and thermal effect on the hydrostatic circular pad, three cases are considered as follows:
Case I: Only hydrodynamic effect (dimensionless parameter 0.3);
Case II: Only thermal effect;
Case III: The combined hydrodynamic and thermal effect.
Fig. 2 shows the pressure distributions for the three cases considering the radial roughness. The values of the pressure at the radius direction are in the following order: Case III pressure < Case II pressure < Case I pressure. For Case I, the hydrodynamic effect causes the uneven pressure distribution, in which the pressure in the velocity direction is more than that of the opposite direction. Correspondingly, for Case II, the thermal effect causes the pressure lower than initial state. Case III is affected by both the hydrodynamic and thermal effect. Since the load-carrying capacity is determined by the pressure distribution of the circular pad, the load-carrying capacity is in the following order: Case III < Case II < Case I, in which the thermal effect causes the load-carrying capacity lower 13.3 % for the hydrodynamic parameter 0.3.
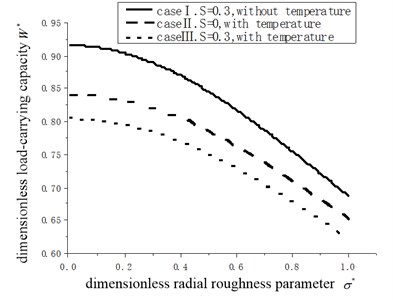
For the load-carrying capacity of circular pad, the hydrodynamic effect caused by velocity is less than the thermal effect because the viscosity and density of the lubricant film is dependent on the temperature during the operating process. In Fig. 3, it is observed that the dimensionless load-carrying capacity gradually decreases with the increase of dimensionless radial roughness parameter . It is divided two parts in 0.3: the flat zone and linear gradient zone. The load-carrying capacity decreases slowly with the increase of dimensionless roughness in the flat zone. However, it sharply falls in the linear gradient zone, which indicates that the load-carrying capacity is greatly affected by the dimensionless radial roughness 0.3.
The large dimension of heavy-duty hydrostatic rotary table causes the linear velocity of guide rail relatively higher, which can affect seriously the flow state of lubricant film of the circular pad when the table rotates at a higher speed. Therefore, the hydrodynamic effect should not be ignored for the analysis of stability of lubricant film. Fig. 4 shows the dimensionless pressure changes with respect to the dimensionless hydrodynamic parameter . In this model, the radial roughness is considered and energy equation is neglected. The uneven pressure distribution is strengthened with the increase of hydrodynamic parameter . The dimensionless hydrodynamic parameter can only alter the pressure distribution rather than the load-carrying capacity of circular pad. However, the load-carry capacity of circular pad can be affected by the roughness of surface, hydrodynamic, and thermal effect of circular pad.
Fig. 2The pressure distribution for three cases at σ*= 0
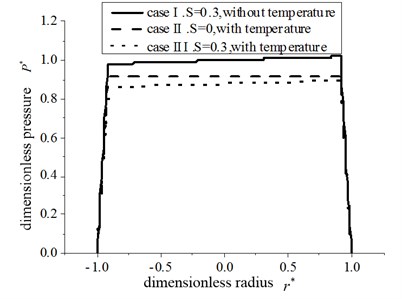
Fig. 3The relationship of load-carrying capacity and dimensionless radial roughness σ*
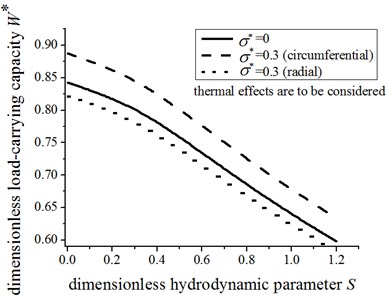
Therefore, the surface roughness and energy equations should be taken into account in analyzing the variation of load-carrying capacity in radial and circumferential roughness model, as shown in Fig. 5. It can be observed that the load-carrying capacity decreases as the increase of dimensionless hydrodynamic parameter . The load-carry capacity considering the radial roughness (0.3) is cut down 3.5 % than that with roughness 0. In contrast to the conclusion of radial roughness, the load-carrying capacity considering the circumferential roughness (0.3) is increased 5.9 % compared to those of without roughness. Therefore, we can conclude that the circumferential roughness is helpful to improve the load-carrying capacity, nevertheless the radial roughness can decrease the load-carrying capacity. These results are coincident with conclusions in [18].
Fig. 4The variation of the dimensionless pressure under different dimensionless hydrodynamic parameter S
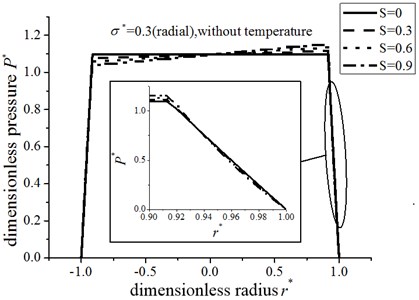
Fig. 5The effect of surface roughness on the load-carrying capacity
Actually, the support performance of the circular pad is affected by the combined thermal and hydrodynamic characteristics. Figs. 6 and 7 show the variation of pressure distribution for the radial and circumferential roughness model with energy equation, respectively. With the increase of dimensionless hydrodynamic parameter , the hydrodynamic and thermal effects increase. The pressure of recess is decreased and the curve of pressure is more declining. For the radial roughness and energy model, compared to the hydrodynamic parameter 0, the pressure in the center of pad is reduced 4.3 %, 13.3 % and 22.4 % when 0.3, 0.6 and 0.9, respectively. At the same conditions, it is reduced 4.1 %, 12.9 and 21.9 % for the circumferential roughness and thermal effect, respectively.
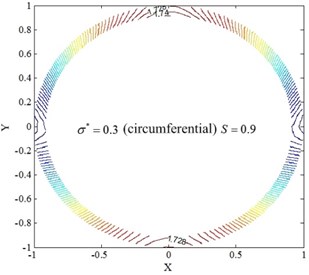
Figs. 8 and 9 depict the mean temperature distribution for the radial and circumferential roughness, respectively. The resistive oil edge of circular pad is expanded from 0 to . The temperature rises rapidly with the increasing of , in which the temperature for the radial roughness model is slightly less than that of the circumferential roughness model. However, the variation law for both models is similar, in which the maximum temperature rising happens at and .
Fig. 6The pressure distribution for radial roughness and energy equation
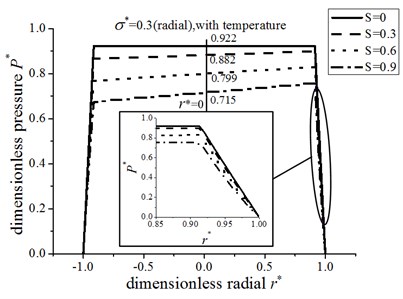
Fig. 7The pressure distribution for circumferential roughness and energy equation
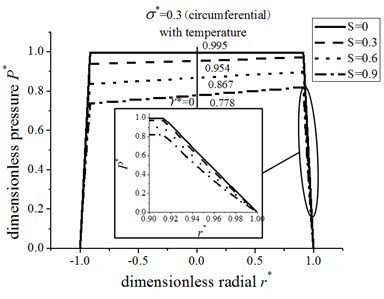
Fig. 8The temperature distribution for radial roughness and energy equation
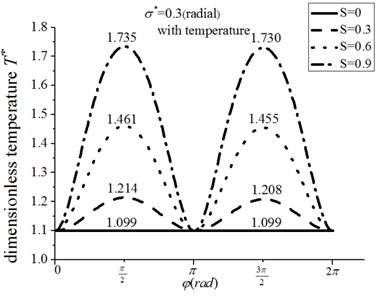
Fig. 9The temperature distribution for circumferential roughness and energy equation
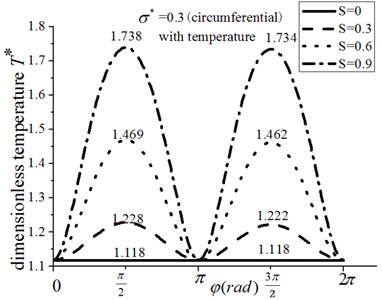
It is difficult to descript the distribution of temperature rising for the restive oil edge in Figs. 8 and 9. Therefore, the temperature field is introduced for the radial and circumferential roughness model, as shown in Figs. 10, 11. The temperature is even distributed for the zero velocity, and slightly lower from outer edge to inner edge in the radial direction. When the rotary table rotates, the temperature of lubricant film in the resistive oil edge will increase with the increase of rotating speed and will be uneven distributed, in which the maximum temperature rising is in the direction of rotating speed (0, 1). Compared to the dimensionless hydrodynamic parameter 0, the temperature risings are 10.4 %, 32.9 %, 58.2 % at the 0.3, 0.6, 0.9, respectively. The results show that the temperature of lubricant film will significantly increase with the increase of , which can rapidly reduce the viscosity of lubricant. It is the main reason of cutting down load-carrying capacity of circular pad. Correspondingly, the hydrodynamic effect does not affect the load-carrying capacity, but the pressure distribution. As a result, the stability of hydrostatic rotary table is decreased with the increasing of .
Fig. 10Temperature field of restive oil edge for radial roughness model
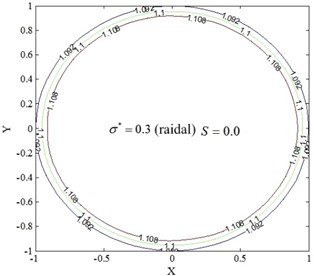
a)0
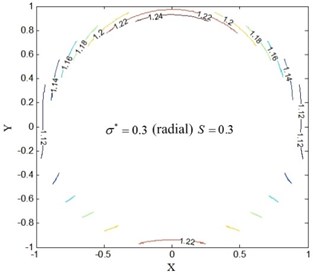
b)0.3
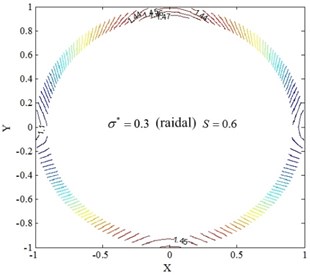
c)0.6
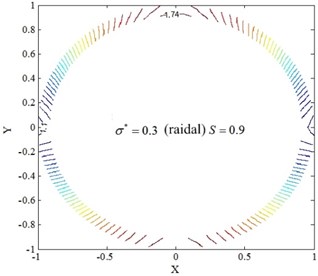
d)0.9
Fig. 11Temperature field of restive oil edge for circumferential roughness model
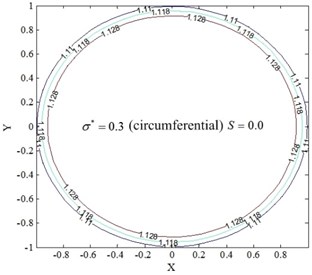
a)0
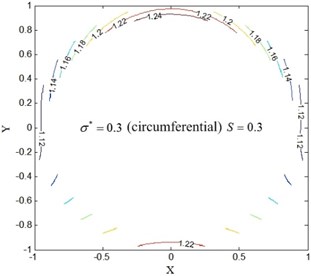
b)0.3
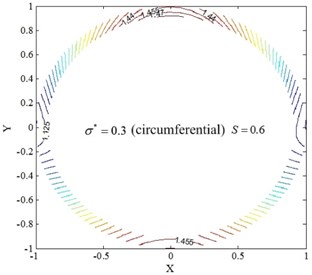
c)0.6
d)0.9
6. Conclusion
In this paper, the thermal, hydrodynamic effect and their coupling effects are analyzed based on a coupled energy equation with mean Reynolds equation for the hydrostatic circular pad of heavy-duty rotary table. Comparing with smooth surface model, the circumferential roughness can improve the load-carrying capacity, but the radial roughness can reduce the load-carrying capacity of heavy-duty rotary table. The uneven pressure distribution is strengthened with the increase of hydrodynamic parameter . The temperature of lubricant film will significantly increase with the increase of , which can cut down the load-carrying capacity of circular pad. As a result, the combine effect of roughness, thermal and hydrodynamic effect should be taken into account in analyzing the performance of the heavy-duty rotary table.
References
-
Fuller D. D. Theory and Practice of Lubrication for Engineers. John Wiley and Sons, New York, 1956.
-
Rippel H. C. Cast Bronze Hydrostatic Bearing Design Manual. Cast Bronze Bearing Institute, Inc., Clevelan, 1963.
-
Rowe W. B. Hydrostatic and Hybrid Bearing Design. Butterworths, London/Boston, 1983.
-
Patir N., Cheng H. S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. Journal of Tribology, Vol. 100, Issue 1, 1987, p. 12-17.
-
Patir N., Cheng H. S. Application of average flow model to lubrication between rough sliding surfaces. Journal of Tribology, Vol. 101, Issue 2, 1979, p. 220-229.
-
Christensen H. Stochastic model for hydrodynamic lubrication of rough surfaces. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, Vol. 184, 1969, p. 1001-1013.
-
Christensen H., Tonder K. The hydrodynamic lubrication of rough bearing surfaces of finite width. Journal of Tribology, Vol. 93, Issue 3, 1971, p. 324-329.
-
Garratt Hibberd Cliffe Centrifugal inertia effects in high-speed hydrostatic air thrust bearings. Journal of Engineering Mathematics, Vol. 76, 2012, p. 59-80.
-
Christensen H., Tonder K. The hydrodynamic lubrication of rough bearing surfaces of finite width. Journal of Tribology, Vol. 93, Issue 3, 1971, p. 324-329.
-
Osterle J. F., Hughes W. F. The effect of lubricant inertia in hydrostatic thrust-bearing lubrication. Wear, Vol. 1, 1985, p. 465-471.
-
Dowson D. Inertia effects in hydrostatic thrust bearings. Journal of Basic Engineering, Vol. 83, 1961, p. 227-234.
-
Chow C. Y. A non-central feeding hydrostatic thrust bearing. Journal of Fluid Mechanics, Vol. 72, 1975, p. 113-120.
-
Dowson D. Inertia effects in hydrostatic thrust bearings. Journal of Fluids Engineering, Vol. 83, Issue 2, 1961, p. 227-234.
-
Bouyer J., Fillon M. On the significance of thermal and deformation effects on a plain journal bearing subjected to severe operating conditions. Journal of Tribology, Vol. 126, 2004, p. 819-822.
-
Serrato R., Maru M. M., Padovese L. R. Effect of lubricant viscosity grade on mechanical vibration of roller bearings. Tribology International, Vol. 40, 2007, p. 1270-1275.
-
Wang Chang-min Analysis temperature field of hydrostatic bearing based on ANSYS. Mechanical Management and Development, Vol. 23, Issue 5, 2008, p. 101-104.
-
Kapur V. K., Verma K. The Simultaneous effects of inertia and temperature on the performance of a hydrostatic thrust bearing. Wear, Vol. 54, Issue 1, 1979, p. 113-122.
-
Lin Qiyin Analysis on the lubrication performances of journal bearing system using computational fluid dynamics and fluid-structure interaction considering thermal influence and cavitation. Tribology International, 2013, p. 648-615.
-
Sinha P., Getachew A. THD analysis for slider bearing with roughness: special reference to load generation in parallel sliders. Acta Mechanica, Vol. 207, 2009, p. 11-27.
Cited by
About this article
This research is supported by National Natural Science Foundation of China (No. 51375025, No. 51575009), National Science and Technology Major Project of China (No. 2013ZX04013-011, No. 2015ZX04014-021) and Jing-Hua Talents Project of Beijing University of Technology.
Yida Wang had derived and simplified formulas in 3th, 4th parts, and also built the structure of the article. Yongsheng Zhao had a guiding about the coupled energy equation with mean Reynolds equation based on the Christensen’s stochastic model of rough surfaces. Ligang Cai provided the understand of data processing. Zhifeng Liu’s contribution is the simulation about pressure distribution. Qiang Cheng had the contribution on application of the finite difference method.
