Abstract
The disaster in queueing system with second optional service is considered. Arriving customer of this system will receive the essential service and optional second service if needed. When the system is interrupted by the disaster, the server initiates the repair period making all the customer leave the system immediately. The server, when idle, takes single vacation. The disaster cannot happen when server is under vacation or in repair period. The above queueing system is analysed using supplementary variable technique to obtain the probability generating function for various parameters and effects of parameters are explained graphically with numerical illustrations.
Highlights
- Disaster rate affecting the production id been analysed.
- Evaluation of the performance measures via expected waiting time and expected queue length of the raw material of the queuing model.
- Relationships between arrival and waiting time, disaster and queue length and more on is visually using numerical illustration.
1. Introduction
The disaster otherwise named as catastrophes can be seen in manufacturing systems, communication systems and many more. As disaster removes all customers immediately from the system, it is extensively modelled by many researchers.
The concept of disaster in Queueing models were introduced by Towsley and Tripathi in analysing the distributed data base system that undergoes failure. Arumuganathan R and Jeyakumar S [1] studied steady state analysis of a bulk queue with multiple vacations, setup times with N-policy and closedown times. Bu, Q., and Liu, L. [2] analyzed M/G/1 clearing queueing system with setup time and multiple vacations for an unreliable server. Chakravarthy S. R [3] analyzed a disaster Queue with Markovian arrivals and impatient customers. Chang, F. M., Liu, T. H., and Ke, J. C. [4] studied an unreliable-server retrial queue with customer feedback and impatience. Choudhury, G., and Kalita, C. [5] analyzed M/G/1 queue with two types of general heterogeneous service and optional repeated service subject to server’s breakdown and delayed repair. George C. Mytalas, Michael A. Z. Azanis [6] studied queueing system with disasters and repairs under MAV policy. George C. Mytalas and Michael A. Zazanis [7] analyzed Bernoulli feedback queues subject to disasters: a system with batch Poisson arrivals under a multiple vacation policy. Jain, M., and Singh, M. [8] analyzed markov queueing model with feedback, discouragement and disaster. Jeyakumar S and Senthilnathan B [9] Modelled and analysed queue with multiple vacation, setup time, closedown time server breakdown without interruptions. Jiang T., Liu L. [10] analysed G1/M/1 queue in a multi-phase service environment with disaster and working breakdowns. Jingjing Y. E., Liu Liwei and Jiang Tao [11] analysed single server queue with disasters and repairs under Bernoulli vacation schedule. Kim B. K. and Lee D. H. [12] modelled and analysed M/G/1 Queue with disasters and working Breakdowns. Lakshmi Priya M., Janani B. [13] studied single server queue with disasters and repairs under Bernoulli working vacation schedule. Mian Zhang and Shan Gao [14] studied the disasters queue with working breakdowns and impatient customers. Nitin Kumar, Farida P. Barbhuiya and Umesh C. Gupta [15] analysed Geometric catastrophe model with discrete-time batch renewal arrival process. Park H. M., Yang W. S., Chae K. C. [16] analysed G1/Geo/1 Queue with disaster. Rajadurai, P., Saravanarajan, M. C., and Chandrasekaran, V. M. [17] studied M/G/1 feedback retrial queue with subject to server breakdown and repair under multiple working vacation policy. Shan Gao, Jinting Wang and Tien Van Do [18] analysed discrete-time repairable queue with disasters and working breakdowns. Sudhesh R and Sebasthi Priya R [19] analysed discrete-time Geo/Geo/1 queue with feedback, repair and disaster. Li, K., and Wang, J. [20] analysed Equilibrium balking strategies in the single server retrial queue with constant retrial rate and catastrophes.
The literature study of the researchers in Markovian queue with disaster under different parameter motivated to study the effect of disaster in Markovian queue with optional service under single vacation policy. There are works in bulk arrival, service under disaster and queues with optional service, but on motivation from literature study, novelty in the described model is linking bulk arrival with optional service and disaster to evaluate the performance measures in arbitrary epoch.
Importance and contribution of study is to find the disaster rate affecting the production, to evaluate and analyze the performance measures of the queuing model with numerical illustrations to establish results in the real word existing scenario.
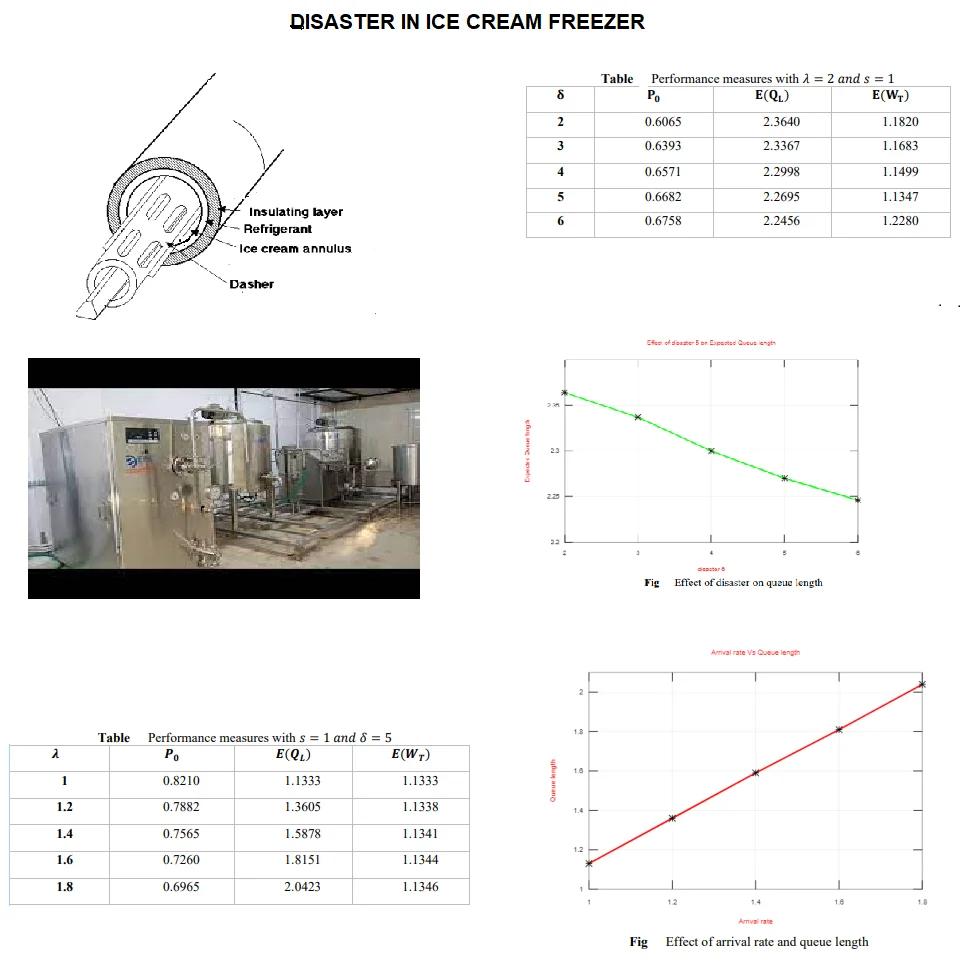
The queue with optional service under disaster and repairs with single vacation can be identified in ice-cream manufacturing unit. When raw material reaches the unit, it is immediately sent to mixer which is essential service and adding up flavour is a manual process which is optional service. Once it is mixed up, it is poured into mould and kept in dipping freezer. When sudden freezer burn (disaster) happens in freezer, the entire process has to stop since the mixed-up raw material can’t be kept for long period. Before starting up next slot of opening the raw material for mix-up, the server can take single vacation if needed because raw material should be fresh for good taste and flavour.
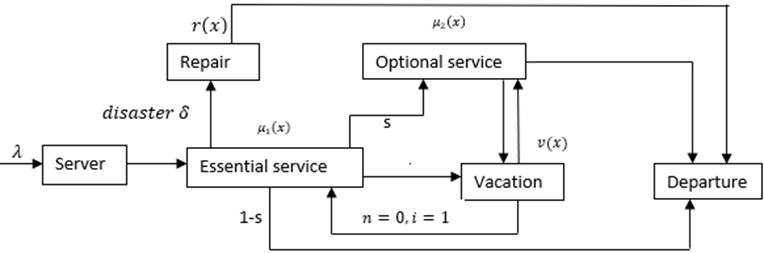
2. Mathematical model
In a compound Poisson process, a batch of customers , with the parameters , and probability joins the system in the minimal duration of time . Each and every customer who arrives at the system is provided with first essential service under first come, first serve discipline. Customer is served one by one in the batch. Let be the hazard rate function of the first essential service with , where is the general distribution function with the corresponding density function and mean . After the first service is completed, the optional service may be opted with the probability or leave the system with the probability For optional service, let with , where is the general distribution function with the corresponding density function and mean . Once the server completes his essential and optional service to the customer, the server may take vacation when he is idle. Let be the rate function of the vacation with where is the general distribution function with the corresponding density function and mean . Finally, disaster is assumed to happen in the system during essential service, since optional service is the manual service. With rate of the disaster , it removes all the customers including one is been served from the system and the system is immediately moved to repair period. Let be the hazard rate function of the repair period with , where is the general distribution function with density function and mean
Fig. 1Schematic diagram of the queueing system
3. Notations and abbreviations
At time , let the system size be . Also, let be the random variable corresponding to server’s status.
Let , 1, 2 and be introduced as supplementary variables to obtain a Markov process.. Limiting probabilities are defined to derive Kolmogorov chapman equation as:
4. Steady state differential equations using supplementary variable technique
Governing equations for various states of the system are framed for :
With the boundary conditions:
To obtain PGF, we multiply the Eqs. (2-11) with certain powers of and sum it over , to obtain:
As the system has no customer after immediate vacation and repair time that comes after disaster, we have:
5. PGF of queue for various states:
At an arbitrary epoch, the PGF of the server is under busy state, repair state and in vacation are obtained from the explicit expressions:
where and .
If possible, using Rouche’s theorem, let be the unique solution of . In that case equality becomes, .
The PGF of the system at epoch of essential service to the customer is given as:
The PGF of the system at epoch of optional second service to the customer is given as:
The PGF of the system at epoch under repair is given as:
The PGF of the system at epoch of under vacation is given as:
Using the normalizing condition at , the probability is obtained when the server being idle as:
Finally, the total PGF of queue size is obtained at as:
Also, due disaster the PGF of total customers removed from the system is given as:
6. Performance measures
Expected queue length (and waiting time is obtained using L’ Hospital’s rule from the Eq. (26):
where , , .
Let , , are the mean service time of all the states; , , be the second moment of states in different epoch. Using little’s formula, the expected waiting time is calculated as:
7. Numerical illustration
A numerical approach is carried on to evaluate the various states of the distribution. , , are assumed to be in exponential parameter respectively. Arrival rate is with service rate and . Whereas disaster may take place with rate .
Average queue length and mean waiting time are computed and tabulated below with assumption of arrival and vacation as single.
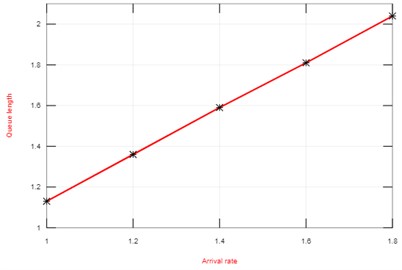
From Table 1 and Fig. 2 it is understood that when probability of second optional service increases, length of the queue and waiting time to be increased. From Table 2 and Fig. 3, queue length and waiting time decreases as the disaster rate increases. Finally, from Table 3 and Fig. 4 when arrival rate increases then length of the queue and waiting time of the server increases.
Table 1Performance measures with λ=2 and δ=2
0 | 0.6521 | 1.8464 | 0.9232 |
0.25 | 0.6401 | 1.9829 | 0.9915 |
0.5 | 0.6285 | 2.1146 | 1.0573 |
0.75 | 0.6173 | 2.2415 | 1.1207 |
1 | 0.6065 | 2.3640 | 1.1820 |
Fig. 2Prob. of second optional service versus queue length and waiting time
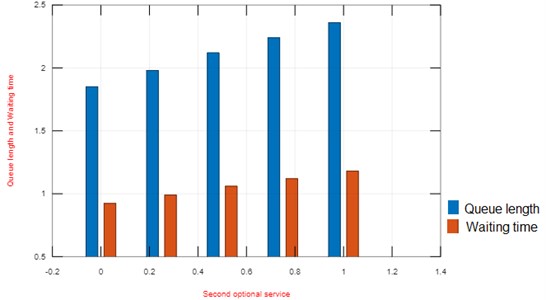
Table 2Performance measures with λ=2 and s=1
2 | 0.6065 | 2.3640 | 1.1820 |
3 | 0.6393 | 2.3367 | 1.1683 |
4 | 0.6571 | 2.2998 | 1.1499 |
5 | 0.6682 | 2.2695 | 1.1347 |
6 | 0.6758 | 2.2456 | 1.2280 |
Fig. 3Effect of disaster on queue length
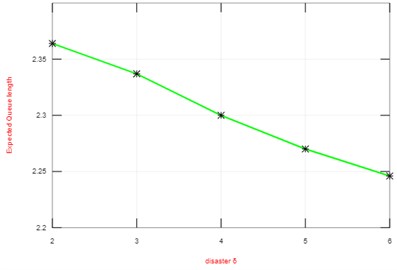
Table 3Performance measures with s=1 and δ=5
1 | 0.8210 | 1.1333 | 1.1333 |
1.2 | 0.7882 | 1.3605 | 1.1338 |
1.4 | 0.7565 | 1.5878 | 1.1341 |
1.6 | 0.7260 | 1.8151 | 1.1344 |
1.8 | 0.6965 | 2.0423 | 1.1346 |
Fig. 4Effect of arrival rate and queue length
8. Conclusions
In this Paper, Queue with the second optional service with single vacation is taken into consideration for disaster and repairs. We derive the queue size distributions for various steady-states with quality metrics and special cases using the supplementary variable technique. Additionally, we've provided numerical examples to illustrate the approach, which amply demonstrate how disasters affect waiting times and queue length with the second optional service. From the numerical illustration, it is observed that when arrival rate and probability for second optional service increases, queue length and waiting time of the customer increases as well as when disaster rate increases queue length and of the server decreases and waiting time of the customer decreases.
References
-
R. Arumuganathan and S. Jeyakumar, “Steady state analysis of a bulk queue with multiple vacations, setup times with N-policy and closedown times,” Applied Mathematical Modelling, Vol. 29, No. 10, pp. 972–986, Oct. 2005, https://doi.org/10.1016/j.apm.2005.02.013
-
Q. Bu and L. Liu, “An M/G/1 clearing queueing system with setup time and multiple vacations for an unreliable server,” Communications in Statistics – Theory and Methods, Vol. 48, No. 11, pp. 2810–2826, Jun. 2019, https://doi.org/10.1080/03610926.2018.1473426
-
S. R. Chakravarthy, “A disaster Queue with Markovian arrivals and impatient customers,” Applied Mathematics and Computation, Vol. 214, No. 1, pp. 48–59, Aug. 2009, https://doi.org/10.1016/j.amc.2009.03.081
-
F.-M. Chang, T.-H. Liu, and J.-C. Ke, “On an unreliable-server retrial queue with customer feedback and impatience,” Applied Mathematical Modelling, Vol. 55, pp. 171–182, Mar. 2018, https://doi.org/10.1016/j.apm.2017.10.025
-
G. Choudhury and C. R. Kalita, “An M/G/1 queue with two types of general heterogeneous service and optional repeated service subject to server’s breakdown and delayed repair,” Quality Technology and Quantitative Management, Vol. 15, No. 5, pp. 622–654, Sep. 2018, https://doi.org/10.1080/16843703.2017.1331499
-
G. C. Mytalas and M. A. Zazanis, “AnMX/G/1 queueing system with disasters and repairs under a multiple adapted vacation policy,” Naval Research Logistics (NRL), Vol. 62, No. 3, pp. 171–189, Apr. 2015, https://doi.org/10.1002/nav.21621
-
G. C. Mytalas and M. A. Zazanis, “Performance analysis for Bernoulli feedback queues subject to disasters: a system with batch Poisson arrivals under a multiple vacation policy,” Quality Technology and Quantitative Management, Vol. 20, No. 1, pp. 113–146, Jan. 2023, https://doi.org/10.1080/16843703.2022.2092954
-
M. Jain and M. Singh, “Transient analysis of a Markov queueing model with feedback, discouragement and disaster,” International Journal of Applied and Computational Mathematics, Vol. 6, No. 2, pp. 1–14, Apr. 2020, https://doi.org/10.1007/s40819-020-0777-x
-
S. Jeyakumar and B. Senthilnathan, “Modelling and analysis of a M^X/G(a,b)/1 queue with multiple vacation, setup time, closedown time server breakdown without interruptions,” International Journal of Operational Research, Vol. 19, No. 1, p. 114, 2014, https://doi.org/10.1504/ijor.2014.057849
-
T. Jiang and L. Liu, “The GI/M/1 queue in a multi-phase service environment with disasters and working breakdowns,” International Journal of Computer Mathematics, Vol. 94, No. 4, pp. 707–726, Apr. 2017, https://doi.org/10.1080/00207160.2015.1128531
-
J. Ye, L. Liu, and T. Jiang, “Analysis of a Single-Sever Queue with Disasters and Repairs Under Bernoulli Vacation Schedule,” Journal of Systems Science and Information, Vol. 4, No. 6, pp. 547–559, Dec. 2016, https://doi.org/10.21078/jssi-2016-547-13
-
B. K. Kim and D. H. Lee, “The M/G/1 queue with disasters and working breakdowns,” Applied Mathematical Modelling, Vol. 38, No. 5-6, pp. 1788–1798, Mar. 2014, https://doi.org/10.1016/j.apm.2013.09.016
-
M. L. Priya and B. Janani, “Transient analysis of a single server queue with disasters and repairs under bernoulli working vacation schedule,” Journal of Mathematical and Computational Science, Vol. 11, No. 1, pp. 312–329, 2021, https://doi.org/10.28919/jmcs/5085
-
M. Zhang and S. Gao, “The disasters queue with working breakdowns and impatient customers,” RAIRO – Operations Research, Vol. 54, No. 3, pp. 815–825, May 2020, https://doi.org/10.1051/ro/2019036
-
N. Kumar, F. P. Barbhuiya, and U. C. Gupta, “Analysis of a geometric catastrophe model with discrete-time batch renewal arrival process,” RAIRO – Operations Research, Vol. 54, No. 5, pp. 1249–1268, Sep. 2020, https://doi.org/10.1051/ro/2019074
-
H. M. Park, W. S. Yang, and K. C. Chae, “Analysis of the GI/Geo/1 queue with disasters,” Stochastic Analysis and Applications, Vol. 28, No. 1, pp. 44–53, Dec. 2009, https://doi.org/10.1080/07362990903417938
-
P. Rajadurai, M. C. Saravanarajan, and V. M. Chandrasekaran, “A study on M/G/1 feedback retrial queue with subject to server breakdown and repair under multiple working vacation policy,” Alexandria Engineering Journal, Vol. 57, No. 2, pp. 947–962, Jun. 2018, https://doi.org/10.1016/j.aej.2017.01.002
-
S. Gao, J. Wang, and T. van Do, “Analysis of a discrete-time repairable queue with disasters and working breakdowns,” RAIRO – Operations Research, Vol. 53, No. 4, pp. 1197–1216, Oct. 2019, https://doi.org/https://doi.org/10.1051/ro/2018057
-
R. Sudhesh and R. S. Priya, “An analysis of discrete-time Geo/Geo/1 queue with feedback, repair and disaster,” International Journal of Operational Research, Vol. 35, No. 1, p. 37, 2019, https://doi.org/10.1504/ijor.2019.10021032
-
K. Li and J. Wang, “Equilibrium balking strategies in the single-server retrial queue with constant retrial rate and catastrophes,” Quality Technology and Quantitative Management, Vol. 18, No. 2, pp. 156–178, Mar. 2021, https://doi.org/10.1080/16843703.2020.1760464
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Jeyakumar S: project administration, supervision, validation. Logapriya B: conceptualization, formal analysis, investigation, methodology, visualization, writing – review and editing.
The authors declare that they have no conflict of interest.
