JTC online comprehensive fault diagnosis method based on angle feature and linear trend feature

2.1. Mathematical model of compensation capacitor and tuning region

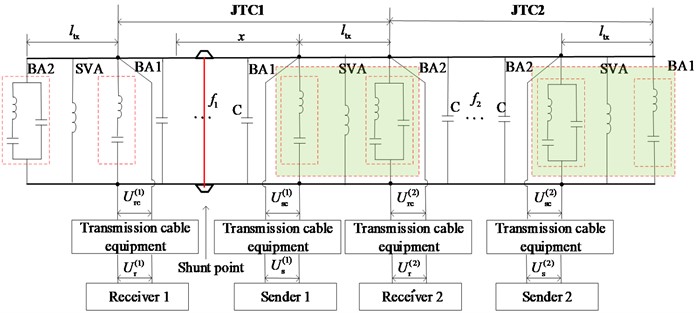
JTC is mainly composed of sending and receiving terminal equipment and rail lines in this section. The sending end part mainly refers to the tuning equipment and the cable equipment at the sending end and the transmitter; Similarly, the receiving end part mainly includes the tuning equipment at the receiving end, the receiving end cable equipment and the receiver; The rail line includes the rail between the sending end and the receiving end and the compensation capacitor in parallel at equal intervals. When the train runs in track section 1, the JTC under the shunt condition is shown in Fig. 1.

Fig. 1JTC shunt status structure diagram

Through analysis, the relationship between the shunt current and the shunt point is:

At this time, the induced voltage amplitude envelope signal recorded by the locomotive signal is:

where $U_S\left(t\right)$ is the frequency shift signal output by transmitter 1, $\alpha ={\alpha }_1{\alpha }_2$, ${\alpha }_1$ can be approximated as a constant, which is determined by the characteristic parameters the receiving coil and the frequency of JTC signal. ${\alpha }_2$ is a constant, which determined by the internal circuit of the locomotive signal. $R_f$ is the shunt resistor, $G\left(x\right)$ is the four-terminal network transmission matrix from the shunt point to sender 1, $T_p$ is the transmission matrix of four-terminal network for the sending device, $T_t$ is a four-terminal network transmission matrix for the sender tuning zone, $T_g\left(x\right)$ is the four-terminal network transmission matrix of rail line from the train shunt point to the rail surface of the tuning-zone of the sending end.

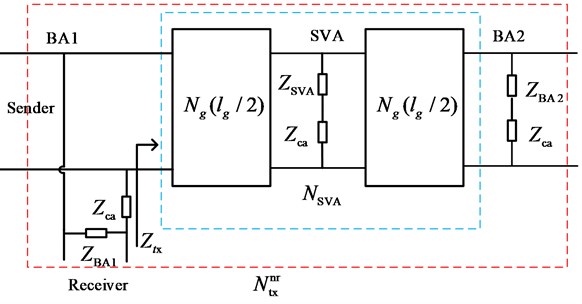
The tuning zone effectively isolated the signal transmission between adjacent track circuits through BA1, BA2 and SVA, which presented a series and parallel resonance relationship between the signals in this section. $Z_{BA1}$, $Z_{BA2}$ and $Z_{SVA}$ respectively represent the impedance values of BA1, BA2 and SVA at the frequency signals in this section; $Z_{ca}$ represents the impedance value of each device when it is connected with the rail; $N_g(l_g/2)$is the equivalent four-terminal network of half rail line length in the tuning zone; At this time, the four-terminal network model of the tuning zone is shown in Fig. 2, where $N_{SVA}$ is the equivalent four-terminal network matrix of the sum of the SVA equivalent impedance of the hollow coil $Z_{SVA}$ and the impedance of the rail connection $Z_{ca}$, then, the equivalent four-terminal network matrix between tuning unit BA1 and BA2 can be expressed as:

$N_g(l_g/2)$ is the equivalent four-terminal network matrix of half rail line length in the tuning zone:

$N_{SVA}$ is the equivalent four-terminal network matrix of hollow coil SVA:

$Z_{tx}$ is the apparent impedance from tuning region BA1 to BA2, expressed as:

When the tuning zone is fault-free, the equivalent four-terminal network matrix at the sending end is $N_{tx}^{nr}$:

2.2. Compensation capacitor and tuning zone fault modeling and impact analysis

The compensation capacitor and BA1 and BA2 and SVA are connected to the rail through rail lead wiring, due to the complex operating environment and man-made damage, the compensation capacitor disconnection or the value of capacitor dropping or the fault of tuning zone will be caused.

Fig. 2JTC Tuning zone normal state four terminal network model

(ⅰ) When a line break fault occurs in BA1, its fault equivalent four-terminal network model can be treated the value of $Z_{BA1}$ as infinity, that is, it can be simulated according to the disconnection state. The four-terminal network model of the tuning region under BA1 disconnection is shown in Fig. 3.

Fig. 3Four-terminal network model of tuning zone when BA1 fails

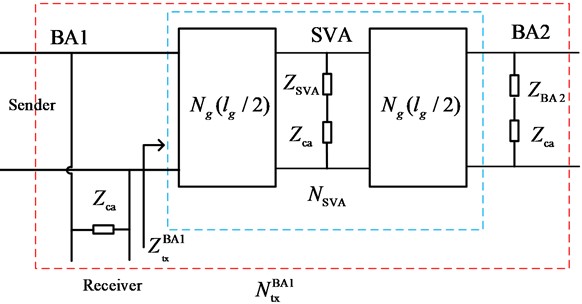
It can be obtained that the equivalent four-terminal network matrix of the tuning-zone of the sender under BA1 disconnection is $N_{tx}^{BA1}$:

(ⅱ) when BA2 breaks, its equivalent circuit model is shown in Fig. 4, where $Z_{G{D}^{\left(2\right)}}$ is the apparent impedance from the tuning region at the receiving end of track circuit 1 to the sending end of track circuit 2:

$Z_{BA{2}^{\left(1\right)}}^{G{D}^{\left(2\right)}}$ is the apparent impedance of track circuit 2:

$Z_{BA{1}^{\left(1\right)}}^{BA{2}^{\left(2\right)}}$ is the apparent impedance from BA2 to track circuit 2:

therefore, the equivalent four-terminal network matrix of the tuning-zone of the sender in the case of l BA2 disconnection is:

(ⅲ) according to FIG. 2, the equivalent four-port network matrix of the tuning-zone at the sending end under SVA disconnection of the hollow coil is $N_{tx}^{SVA}$:

Fig. 4The equivalent circuit model when BA2 is fault

Eqs. (1-14) are used, according to the electrical parameters of the uninsulated track circuit, select a section of track circuit and simulate the states of fault free, compensation capacitor disconnection and tuning equipment fault respectively. The corresponding simulation conditions: the carrier signal frequency of track circuit 1 is $f_1=$2000 Hz and 2 is $f_2=$2600 Hz. The length of track circuit 1 is $l_{g1}=$1099 m and 2 is $l_{g2}=$1442 m. The number of compensation capacitors are $n_{c1}=$11 and $n_{c2}=$18, the value of $c_{v1}=$40 μF and $c_{v2}=$50 μF, the shunt resistance is $R_f=$0.15 Ω, the ballast resistance is $R_G=$ 1 Ω·km, The result is shown in Fig. 5.

As can be seen from Fig. 5, when the track circuit is not equipped with compensation capacitor, $I\left(x\right)$ is the normalized shunt current and will attenuate greatly from the sending end to the receiving end.

As can be seen from Fig. 6, the track circuit equipped with compensation capacitor make the shunt current present a “wave” rise from the receiving end to the sending end of the local section under the condition of no fault. When the compensation capacitor breaks the line, $I\left(x\right)$ will attenuate rapidly at the breakpoint, making the angle between the left and right side tangents of the breakpoint curve increased to 180 degrees.

Fig. 5Normalized of all compensation capacitor failures

Fig. 6Normalized of fault-free and C5, C9 disconnection

Fig. 7Normalized I(x) of fault-free and tuning device failure

As can be obtained from Fig. 7, when the tuning equipment fails, the overall trend between the three compensation capacitors near the sending end will change.

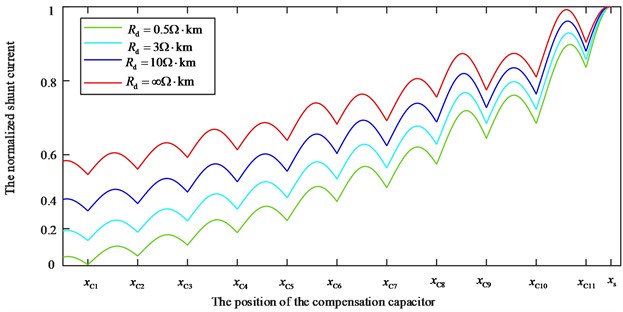
As shown in Fig. 8, the fluctuation of ballast resistance will affect the attenuation rate of $I\left(x\right)$. The larger the resistance is, the smaller the attenuation rate will be, and the greater the vice versa. However, the change of ballast resistance will not change the overall trend of the curve and the tangent angle at the position of compensation capacitor.

Fig. 8Normalized I(x) of fluctuation on ballast resistor

3.1. Angle feature extraction

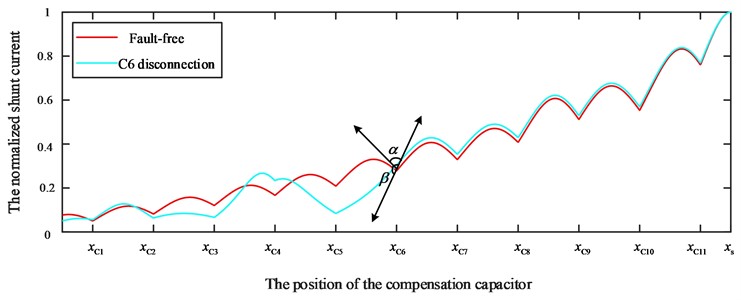
According to Fig. 9 and the above analysis, when line breaking occurs on the compensation capacitor C6, the included angle of the tangent vector on the left and right sides of C6 increases from $\alpha$ to $\beta$. Therefore, the included angle of the tangent vector on the left and right sides of the compensation capacitor is used as the basis for fault feature extraction. In order to obtain the tangent vectors of the left and right sides of the compensation capacitor, the curve equations of both sides should be obtained respectively. According to the data set $I\left(x\right)$ obtained by simulation, the data $\left\{(x_l,y_l),l=\mathrm{0,1},2,\cdots ,t\right\}$ at the distance of $t$ between the two sides of the compensation capacitor and its position is selected for polynomial fitting:

where $m$ is the number of compensation capacitor. Then we can see from the above formula that 2$m$ curves need to be fitted. Set the fitting model be:

Fig. 9Tangent vector angle extraction diagram for C6 normal and C6 disconnection

The least square method was used to determine the coefficients of $a_0,a_1,\cdots a_n$, assuming the weight of each data point is 1, $\phi (a_0,a_1,\cdots ,a_n)$ is minimized, that is minimizing:

then there is:

where $j=\mathrm{0,1},2,\cdots ,t$, thus:

According to Eqs. (15)-(17), the equations can be obtained as follows by solving Eq. (18):

This equation is called the normal equation of polynomial fitting.

By setting:

There is $XA=Y$, thus $A=X^{-1}Y$, Eq. (17) can be obtained by solving the coefficient vector A from the matrix equation. The left and right side tangent vectors of the fitting polynomial at $x_i$ are$v_1=\left(1,\frac{d\left(S^{-}\left(x_i\right)\right)}{d{x}_i}\right)$ and $v_2=\left(1,\frac{d\left(S^{+}\left(x_i\right)\right)}{d{x}_i}\right)$, the angle between the left and right side tangent vectors of theta is ${\theta }_i=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\frac{v_1\cdot v_2}{‖v_1‖\cdot ‖v_2‖}$, define the fault angle determination indicator as $J_i=\frac{1+\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_i}{2}$, ($0\le J_i<1$).

According to the above analysis and a large number of railway field data, the more serious the reduction of compensation capacitor, the larger the angle of tangent vector $\theta$, the smaller the angle determination index $J_i$, and when the compensation capacitor is broken, $J_i$ is 0.

3.2. Piecewise linear feature extraction

According to the $I\left(x\right)$ simulation curve of tuning equipment fault, the fault characteristics occur in the first three compensation capacitor segments close to the sending end. Therefore. $I\left(x\right)$ is divided by the location of the first three compensation capacitors close to the sending end, that is to say:

where $k=1,\cdots ,\mathrm{}4$, ${l_{k(}}_{m-2)}\left(x_{m-2}\right)$, ${l_{k(}}_{m-2)}\left(x_{m-2}\right)$, ${l_{(}}_{m-2)}\left(x_{m-2}\right)$ refers to the segments sequentially captured at the first three the position of compensation capacitor near the sending end respectively, and linear fitting is carried out on them:

Eq. (22) represents the linear segment obtained by connecting the shunt current at the compensation capacitor. According to Eq. (22), the overall trend of divided fragments $Q_k=[q_{k(m-2)},q_{k(m-1)},q_{km}]$ can be extracted as follows:

According to Eq. (21)-(23), JTC without fault, BA1 broken line, BA2 broken line and SVA broken line were simulated respectively and the overall trend of segment division was extracted, that is $Q_1=\left[\mathrm{1,1},1\right]$, $Q_2=[\mathrm{0,1},1]$, $Q_3=\left[\mathrm{0,0},1\right]$, $Q_4=[\mathrm{0,1},0]$.

3.3. Fault mode diagnosis method

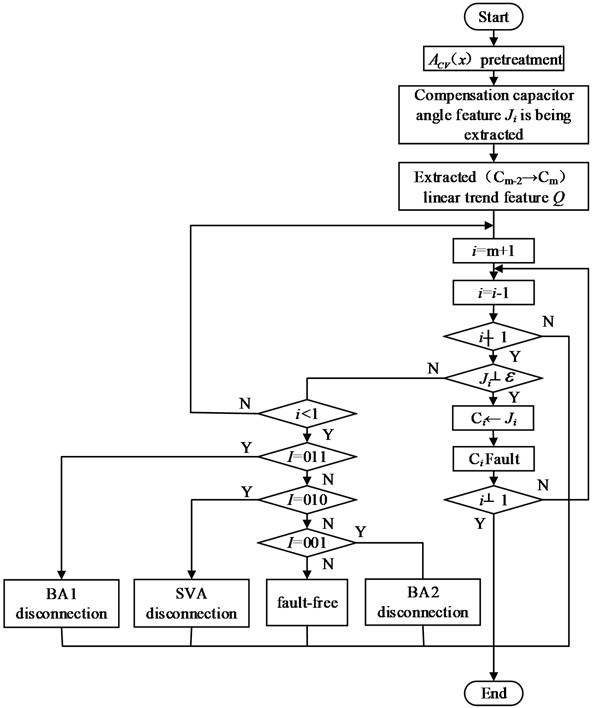
The fault diagnosis process is shown in Fig. 10. The pre-processing of $I\left(x\right)$ includes signal coordinate transformation and amplitude normalization. The signal coordinate transformation adopts spline interpolation method, and the position of compensation capacitor is taken as $I\left(x\right)$ transformed horizontal coordinate to eliminate the influence of train speed change. The angle feature and the linear trend feature vector of $I\left(x\right)$ of the tuning region are first extracted based on the JTC fault feature extraction method proposed in this paper. Then from the sending end, the angle feature $J_i$ of all compensation capacitor are tested to test if they are less than or equal to the decision threshold $\epsilon$. If the conditions are met, the fault $C_i$ will be output and the linear trend feature vectors of the tuned devices will not be tested. If the detection results show that all values $J_i$ are greater than the decision threshold $\epsilon$, it means that no line breaking fault occurs in the compensation capacitor, and the tuning device is detected according to the extracted linear characteristic trend vector $Q$ of the tuning device. Finally, the test result is output.

5.1. Simulation experiment verification

The fault diagnosis algorithm proposed in this paper is used to diagnose the faults in the normal state of JTC and when C4 and C7 are disconnected. The corresponding simulation parameters are set as follows: signal-to-noise ratio $SNR=$50 dB, ballast resistance $R_G=$1 Ω⋅km.

According to the fault diagnosis flow chart shown in Fig. 10, the detection result of compensation capacitor of a certain line electrical detection vehicle is diagnosed, and the detection result is shown in Fig. 11.

Fig. 11I(x) with noise of fault-free and C4, C7 disconnection

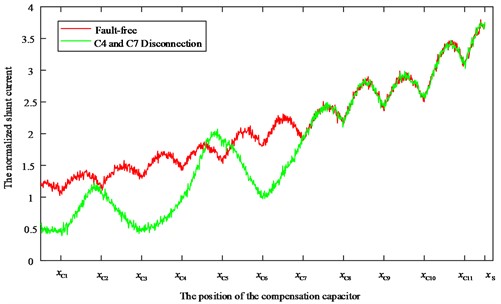
Fig. 12Angle feature vector extraction result of fault-free and C4, C7 disconnection

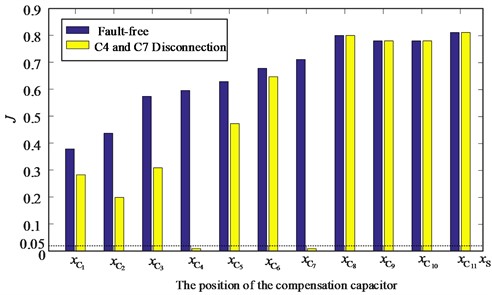
The extracted angle feature extraction results are shown in Fig. 12, the angle feature at the position of C4 and C7 in the figure are less than the decision threshold, and the diagnostic results show that C4 and C7 have line breaking faults.

According to the fault diagnosis flow chart shown in Fig. 10, the detection result of compensation capacitor of a certain line electrical detection vehicle is diagnosed, and the detection result is shown in Fig. 13.

Fig. 13Ixwith noise of fault-free and BA1 disconnection

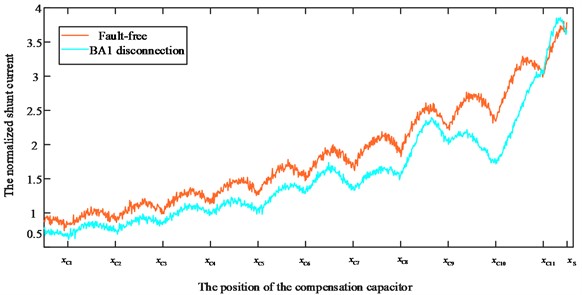
Fig. 14Angle feature extraction results of fault free and BA1 disconnection

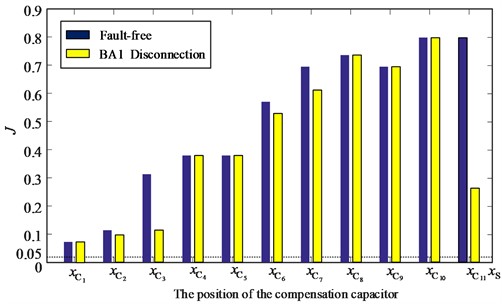
Fig. 15Linear trend feature extraction results of fault-free and BA1 disconnection

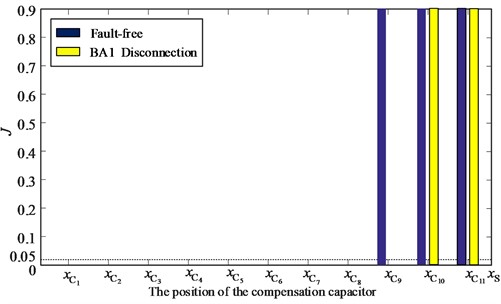
The extraction result of Angle feature in Fig. 14 shows that the compensation capacitor does not fail in Fig. 13, and the linear trend feature is extracted, the extraction result is $Q=[\mathrm{0,1},1]$, as shown in Fig. 15, indicating that BA1 disconnection.

Similarly, the broken line of BA2 was simulated respectively and the overall trend of this section was extracted.

As shown in Fig. 16, the extraction result is $Q_3=[\mathrm{0,0},1]$ it means that BA2 has broken the line.

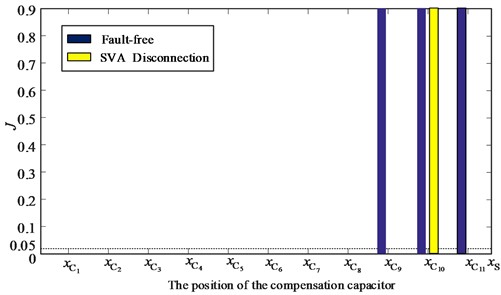
The situation of SVA disconnection was simulated respectively and the overall trend of this section was extracted.

Fig. 16Linear trend feature extraction results of fault-free and BA2 disconnection

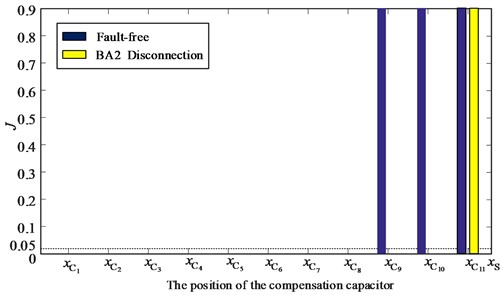
Fig. 17Linear trend feature extraction results of fault-free and SVA disconnection

As shown in Fig. 16, the extraction result is $Q_3=[\mathrm{0,1},0]$ it means that BA2 has broken the line.

The above experiments show that the algorithm has accurate detection effect on multiple compensation capacitor disconnection and tuning equipment breaks.

5.2. Algorithm performance analysis

In order to verify the accuracy of the proposed method in JTC fault diagnosis under different signal-to-noise ratio and ballast resistance fluctuation, according to the above simulation model and the track circuit adjustment table, the signal-to-noise ratio SNR is 30 dB, 40 dB, 50 dB and 60 dB respectively, and the resistance of ballast is 0.5 Ω·km, 1 Ω·km, 3 Ω·km and 5 Ω·km respectively. 100 Ω·km, ∞ Ω·km, selected 69 groups of sample data corresponding to various fault modes (tuning equipment fault, compensation capacitor combination fault) of each parameter, and obtain a total of 1656 groups of sample data including various fault modes. Finally, obtained $h_l$$h_w$$h_x$ and $h_z$ under different signal-to-noise ratio and different ballast resistance, as shown in Table 1 and Table 2.

As can be seen from Table 1 and Table 2, the larger the signal-to-noise ratio SNR is, the larger the value of $h_z$ is, and the value of $h_l$, $h_w$, and $h_x$ also changes to a very small value, and the higher the diagnosis accuracy is. When the SNR is small, the fitting accuracy will be affected, and the extracted angle features will be inaccurate, thus affecting the accuracy of fault diagnosis. The change of ballast resistance has no effect on the fitting accuracy, and the fluctuation of ballast resistance basically does not affect the fault diagnosis rate. When the SNR exceeds 50 dB, no matter how the ballast resistance changes, the diagnosis accuracy exceeds 94.2 %; This method is simpler than deep learning algorithms and decision tree algorithms, and has higher diagnosis accuracy than BP neural network algorithms, and has better flexibility and applicability.