Researching low frequency vibration of automobile-robot

Jia, Yujie; Nguyen, Vanliem

doi:10.21595/rsa.2024.23851

Robotic Systems and Applications

Browse Journal

Submit article

Published: 06 June 2024

Check for updates

Researching low frequency vibration of automobile-robot

Yujie Jia¹

Vanliem Nguyen²

^{1, 2}School of Mechanical and Electrical Engineering, Hubei Polytechnic University, Huangshi, China

^{1, 2}Hubei Key Laboratory of Intelligent Conveying Technology and Device, Hubei Polytechnic University, Huangshi, China

Corresponding Author:

Vanliem Nguyen

Cite the article Download PDF

Downloads 24

Abstract

Automobile-robot (self-driving automobile) is being researched and developed vigorously. When the automobile-robot is moving on the road surface, the low frequency vibration excitation not only influences the ride comfort of the automobile-robot but also strongly affects the durability of the vehicle’s structures. To research the automobile-robot’s vibration in the low frequency region, a dynamic model of the vehicle is established to calculate the vibration equations in the time region. Based on the theory of the Laplace transfer function, the automobile-robot’s vibration equations in the time region are transformed and converted to the vibration equations in the frequency region. Then, the effect of the design parameters and operation parameters on the characteristic of the automobile-robot’s acceleration-frequency is simulated and analyzed to evaluate the ride comfort as well as the durability of the automobile-robot’s structures in the frequency region. The research results show that the design parameters of the stiffness, mass, and road wavelength remarkably affect the characteristic of the automobile-robot’s acceleration-frequency. To reduce the resonant amplitude of the acceleration-frequency in the vertical and pitching direction of the automobile-robot, the stiffness parameters of the automobile-robot's and tires should be reduced while the mass of the automobile-robot’s body should be increased. Additionally, the road’s roughness also needs to be decreased or the road’s quality needs to be enhanced to reduce the resonant amplitude of the automobile-robot’s acceleration-frequency.

1. Introduction

To increase driver comfort, vehicle manufacturers are developing self-driving car systems, also known as automobile-robot. The vibration isolation structure of automobile-robot is similar to the vibration isolation structure of the traditional automobile. The isolation systems of the automobile-robot have been used to reduce the vibration excitations from the road surface transmitted to the automobile-robot’s body. In the design process of the vehicle’s suspension systems, the structures of the suspension system were designed by the spring and damper with the stiffness parameter and damping parameter. The study showed that these parameters greatly affected the ride comfort of the vehicle [1]. In order to enhance the ride comfort of the vehicle or automobile, these design parameters were optimized by the genetic algorithm [2-3]. By searching for the best stiffness and damping parameters for the automobile’s suspension systems, the automobile’s ride comfort has been improved in comparison with the passive suspension systems. However, the automobile’s ride comfort was still low under the high speeds of the automobile’s moving or the automobile’s moving on the poor road surface roughness. Therefore, the automobile’s suspension systems were improved by using the control damping forces of semi-active suspension systems [4-5] or semi-active air suspension systems [6]. The research results showed that with the control damping forces of the semi-active suspension systems used, the automobile’s ride comfort was better than that of the automobile’s optimal suspension systems under different operation conditions. However, the research also indicated that the control performance of the semi-active suspension systems strongly depended on the control method and control rule of the algorithm programs [7-8]. To enhance the control performance, advanced control methods using the Adaboost algorithm and machine learning were applied [9-10]. In the above studies, the dynamic model was established to calculate the vibration equations of the automobile. Then, these vibration equations were built and simulated to compute the automobile’s acceleration responses in the time region. The root mean square values of these acceleration responses were then computed to assess the automobile’s ride comfort based on ISO 2631-1:1997 [11].

However, ISO 2631-1 showed that the ride comfort and health of the driver were also strongly affected by the vehicle’s vibration excitations in the frequency region [11], especially at the excitations in the low frequency from 0.5 to 10 Hz of the road surface when the vehicle is moving. From the random excitations of the road surface built based on ISO 8068 [12], the interaction models of the vehicle and random road surface were established and studied the vibration of the vehicle or cab in the low frequency region [13-14]. Besides, the effect of the design parameters of the isolation systems on the vehicle’s vibrations in the low frequencies was also evaluated [15-16]. The results indicated that the density of resonant frequencies and resonant amplitudes of automobile-robot’s acceleration-frequency response appeared very much in the low frequency region, especially at excitations from 0.5 to 4.0 Hz. This not only affected the driver’s health but also strongly affected the durability of the automobile-robot’s structures and road surfaces. Thus, the resonant frequencies and resonant amplitudes in the automobile-robot’s acceleration-frequency response in this excitation range needed to be minimized. These resonant frequencies and resonant amplitudes were directly impacted by the design parameters and operation parameters of the automobile-robots such as the stiffness, mass, speed, and road surface, etc. Therefore, the effect of the design parameters and operation parameters of the automobile-robots on the driver’s health and the durability in automobile-robot’s structures under different frequency excitations need to be researched and analyzed. However, this issue has not been considered in the existing research.

In this study, a dynamic model of the automobile-robot is established to calculate its vibration equations in the time region. Based on the theory of the Laplace transfer function [17], the automobile-robot’s vibration equations in the time region are transformed and converted to the automobile-robot’s vibration equations in the frequency region. Then, the effect of the automobile-robot’s design parameters and operation parameters on the characteristic of the automobile-robot’s acceleration-frequency is simulated and analyzed to evaluate the automobile-robot’s ride comfort as well as the durability of the automobile-robot’s structures in the frequency region. Enhancing the working performance of the automobile-robot is the goal of this study.

2. Automobile-robot’s mathematical model

2.1. Calculating the vibration equations of the automobile-robot in the time region

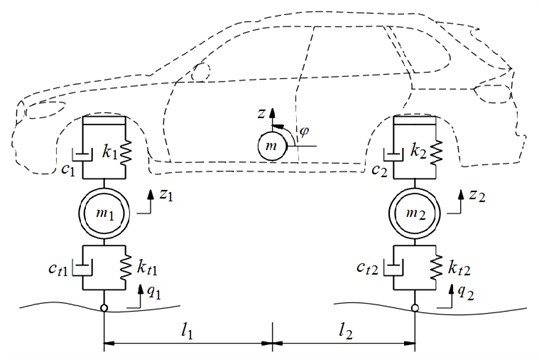
In order to compute an automobile-robot’s vibration equations, based on its actual structure, a 2-D automobile-robot dynamics model is established and shown in Fig. 1, where four degrees of freedom of the automobile-robot including the automobile-robot body’s vertical vibration, automobile-robot’s pitch vibration, front axle’s vibration, and rear axle’s vibration are defined by $z$ , $φ$ , $z_{1}$ , and $z_{2}$ , respectively. The mass of the automobile-robot’s body, front-axle, and rear-axle are also defined by $m$ , $m_{1}$ , and $m_{2}$ , respectively. The stiffness and damping parameters of the front and rear axles are also defined by { $c_{1}$ and $k_{1}$ } and { $c_{2}$ and $k_{2}$ }. The stiffness and damping parameters of front and rear tires are also defined by { $c_{t 1}$ and $k_{t 1}$ } and { $c_{t 2}$ and $k_{t 2}$ }. $l_{1,2}$ and $q_{1,2}$ are the distances and vibration excitations of the automobile-robot and tires.

From the automobile-robot’s dynamics model shown in Fig. 1, its vibration equations are then written by:

1

\{\begin{array}{l} m \ddot{z} + (c_{1} + c_{2}) \dot{z} + (k_{1} + k_{2}) z + \dots \\ + (c_{1} l_{1} + c_{2} l_{2}) \dot{φ} + (k_{1} l_{1} + k_{2} l_{2}) φ - c_{1} {\dot{z}}_{1} - k_{1} z_{1} - c_{2} {\dot{z}}_{2} - k_{2} z_{2} = 0, \\ I \ddot{φ} + (c_{1} l_{1}^{2} + c_{2} l_{2}^{2}) \dot{φ} + (k_{1} l_{1}^{2} + k_{2} l_{2}^{2}) φ + \dots \\ + (c_{1} l_{1} - c_{2} l_{2}) \dot{z} + (k_{1} l_{1} - k_{2} l_{2}) z + - c_{1} l_{1} {\dot{z}}_{1} - k_{1} {l_{1} z}_{1} + c_{2} {l_{2} \dot{z}}_{2} + k_{2} {l_{2} z}_{2} = 0, \\ m_{1} {\ddot{z}}_{1} + (c_{1} + c_{t 1}) {\dot{z}}_{1} + (k_{1} + k_{t 1}) z_{1} - c_{1} \dot{z} - k_{1} z - c_{1} l_{1} \dot{φ} - k_{1} l_{1} φ = c_{t 1} {\dot{q}}_{1} + k_{t 1} q_{1}, \\ m_{2} {\ddot{z}}_{2} + (c_{2} + c_{t 2}) {\dot{z}}_{2} + (k_{2} + k_{t 2}) z_{2} - c_{2} \dot{z} - k_{2} z + c_{2} l_{2} \dot{φ +} k_{2} l_{2} φ = c_{t 2} {\dot{q}}_{2} + k_{t 2} q_{2} . \end{array}

Fig. 1The dynamic model of the automobile-robot

In the research of the automobile-robot’s vibration, the automobile-robot’s vibration in the time region is mainly applied for assessing the automobile-robot’s comfort. However, based on ISO 2631-1:1997 [11], the automobile-robot’s vibration responses in the frequency region also greatly affected the ride comfort and structure in the automobile-robot’s systems. Therefore, in this study, the vibration characteristic of the automobile-robot in the frequency region will be researched and evaluated under different operation conditions of the automobile-robot.

2.2. Calculating the vibration equations of the automobile-robot in the frequency range

To establish the automobile-robot’s vibration equations in the frequency region as well as evaluate the vibration characteristic of the car in the frequency region, based on the automobile-robot’s vibration equation in the time region in Eq. (1), the Laplace transfer function [17] is then used to convert Eq. (1) in the time region ( $t$ ) to the image function ( $s$ ) in the frequency region with the excitation frequency of $ω$ . Herein, $ω = 2 π f$ and $s = d / d t$ .

The theory of the Laplace transfer function is described by: If a vibration function of $n (t)$ operates and depends on the variable time of $t > 0$ in its operation range defined by { $a$ and $b$ }, based on the method of the Laplace transfer function, the image function of $n (t)$ defined by $N (s)$ is expressed as follows:

2

N (s) = \int_{b}^{a} e^{- s t} n (t) d t, s = i ω .

Or:

3

n (t) \to N (s) .

Similarly, based on the theory of the Laplace transfer function, the derivative equations of the image function of $n (t)$ , $\dot{n} (t)$ , and $\ddot{n} (t)$ are also written by [17]:

4

\{\begin{matrix} n (t) \to N (s), \\ \dot{n} (t) \to s N (s) - N (0), \\ \ddot{n} (t) \to s^{2} N (s) - s N (0) - N (0), \\ ⋮ \\ {\overset{⃛}{n}}^{n} (t) \to s^{n} N (s) - s^{n - 1} N (s) - \dots - N (0) . \end{matrix}

From the dynamic model of the car in Fig. 1, at the initial condition of the automobile-robot moving when $t = 0$ , the vibration responses of the automobile-robot’s and front/rear wheel axles are equal to zero ( $z (t) = 0$ , $φ (t) = 0$ , $z_{1} (t) = 0$ , and $z_{2} (t) = 0$ ). Therefore, the derivative equations of their image function at the initial condition when $t = 0$ are also equal to zero ( $N (0) = 0$ ).

Based on the Laplace transfer function in Eqs. (3) and (4), the derivative equations of the automobile-robot body’s vertical vibration $z (t)$ , automobile-robot body’s pitch vibration $φ (t)$ , front axle’s vibration $z_{1} (t)$ , and rear axle’s vibration $z_{2} (t)$ calculated in Eq. (1) at the time region are described by the image functions ( $s$ ) of $Z (s)$ , $Ψ (s)$ , $Z_{1} (s)$ , and $Z_{2} (s)$ in the frequency region as follows:

5

\{\begin{matrix} z (t) \to Z (s), \\ \dot{z} (t) \to s Z (s), \\ \ddot{z} (t) \to s^{2} Z (s), \end{matrix} \{\begin{matrix} φ (t) \to Ψ (s), \\ \dot{φ} (t) \to s Ψ (s), \\ \ddot{φ} (t) \to s^{2} Ψ (s), \end{matrix} \{\begin{matrix} z_{1,2} (t) \to Z_{1,2} (s), \\ {\dot{z}}_{1,2} (t) \to s Z_{1,2} (s), \\ {\ddot{z}}_{1,2} (t) \to s^{2} Z_{1,2} (s), \end{matrix} \{\begin{matrix} q_{1,2} (t) \to Q_{1,2} (s), \\ {\dot{q}}_{1,2} (t) \to s Q_{1,2} (s) . \end{matrix}

Thus, the automobile-robot’s vibration equation of Eq. (1) in the time region is rewritten by the automobile-robot’s vibration equation at the frequency range via the theory of Laplace functions as follows:

6a

\{\begin{matrix} a_{11} Z (s) + a_{12} Ψ (s) + a_{13} Z_{1} (s) + a_{14} Z_{2} (s) = 0, \\ a_{21} Z (s) + a_{22} Ψ (s) + a_{23} Z_{1} (s) + a_{24} Z_{2} (s) = 0, \\ a_{31} Z (s) + a_{32} Ψ (s) + a_{33} Z_{1} (s) + 0 = b_{3} Q_{1} (s), \\ a_{41} Z (s) + a_{42} Ψ (s) + 0 + a_{44} Z_{2} (s) = b_{4} Q_{2} (s), \end{matrix}

or:

6b

[\begin{matrix} a_{11} & a_{12} & \begin{matrix} a_{13} & a_{14} \end{matrix} \\ a_{21} & a_{22} & \begin{matrix} a_{23} & a_{24} \end{matrix} \\ \begin{matrix} a_{31} \\ a_{41} \end{matrix} & \begin{matrix} a_{32} \\ a_{42} \end{matrix} & \begin{matrix} \begin{matrix} a_{33} \\ 0 \end{matrix} & \begin{matrix} 0 \\ a_{44} \end{matrix} \end{matrix} \end{matrix}] [\begin{matrix} Z (s) \\ Ψ (s) \\ \begin{matrix} Z_{1} (s) \\ Z_{2} (s) \end{matrix} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ \begin{matrix} b_{3} Q_{1} (s) \\ b_{4} Q_{2} (s) \end{matrix} \end{matrix}] .

By dividing Eq. (6) by $Q_{1} (s)$ , the matrix of Eq. (6) has been rewritten by:

7

[\begin{matrix} a_{11} & a_{12} & \begin{matrix} a_{13} & a_{14} \end{matrix} \\ a_{21} & a_{22} & \begin{matrix} a_{23} & a_{24} \end{matrix} \\ \begin{matrix} a_{31} \\ a_{41} \end{matrix} & \begin{matrix} a_{32} \\ a_{42} \end{matrix} & \begin{matrix} \begin{matrix} a_{33} \\ 0 \end{matrix} & \begin{matrix} 0 \\ a_{44} \end{matrix} \end{matrix} \end{matrix}] [\begin{matrix} Z (s) / Q_{1} (s) \\ Ψ (s) / Q_{1} (s) \\ \begin{matrix} Z_{1} (s) / Q_{1} (s) \\ Z_{2} (s) / Q_{1} (s) \end{matrix} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ \begin{matrix} b_{3} \\ b_{4} Q_{2} (s) / Q_{1} (s) \end{matrix} \end{matrix}],

where $s = i ω$ , $s^{2} = - ω^{2},$ $a_{11} = - {m ω}^{2} + (k_{1} + k_{2}) + i (c_{1} + c_{2}) ω,$ $a_{12} = a_{21} = (k_{1} l_{1} + k_{2} l_{2}) + i (c_{1} l_{1} + c_{2} l_{2}) ω$ , $a_{31} = a_{13} = - k_{1} - i c_{1} ω$ , $a_{41} = a_{14} = - k_{2} - i c_{2} ω$ , $a_{22} = - {I ω}^{2} + (k_{1} l_{1} l_{1} + k_{2} l_{2} l_{2}) + i (c_{1} l_{1} l_{1} + c_{2} l_{2} l_{2}) ω$ , $a_{32} = a_{23} = - {k_{1} l}_{1} - i c_{1} l_{1} ω$ , $a_{42} = a_{24} = - {k_{2} l}_{2} - i c_{2} l_{2} ω,$ $a_{33} = - {m_{1} ω}^{2} + (k_{1} + k_{t 1}) + i (c_{1} + c_{t 1}) ω,$ $a_{34} = - {m_{2} ω}^{2} + (k_{2} + k_{t 2}) + i (c_{2} + c_{t 2}) ω$ , $b_{3} = k_{t 1} + i c_{t 1} ω$ , and $b_{4} = k_{t 2} + i c_{t 2} ω$ , respectively.

Let $T_{z} = Z (s) / Q_{1} (s)$ , $T_{φ} = Ψ (s) / Q_{1} (s)$ , $T_{z 1} = Z_{1} (s) / Q_{1} (s)$ , and $T_{z 2} = Z_{2} (s) / Q_{2} (s)$ , thus, $T_{z}$ , $T_{φ}$ , $T_{z 1}$ , and $T_{z 2}$ are defined as the vibration’s transfer functions from the road to the automobile-robot body and front/rear axles, respectively.

Based on the calculated results in Refs [17], the result of the acceleration amplitude obtained via $T_{n} =$ { $T_{z}$ , $T_{φ}$ , $T_{z 1}$ , and $T_{z 2}$ } in Eq. (7) under road’s excitations $Q_{1} (s)$ are written as follows:

8

|\ddot{T_{n}}| = ω^{2} \sqrt{X_{n}^{2} + Y_{n}^{2}} = ω^{2} f_{n} (ω) .

2.3. Road’s excitations on car’s wheels

When the automobile-robot is traveling on the road, the vibration excitation of the road described by the harmonic function with its wavelength from 5 m to 10 m and its height from 0.01 m to 0.012 m greatly affects the automobile-robot’s ride comfort and structure [12, 18-19]. This harmonic function mainly causes resonant vibrations in the automobile-robot’s suspension system. Thus, this excitation is used to evaluate the vibration characteristic of the automobile-robot at the frequency range. The road surface’s vibration equation using the harmonic surface at time region has been described as:

9

q_{1} = q_{0} s i n ω t = q_{0} s i n (\frac{2 π}{T}) t .

With the frequency and wavelength of the road defined by $L$ and $l$ , Eq. (9) is then rewritten in the traveling direction of $X$ as follows:

10

q_{1} = q_{0} s i n L X = q_{0} s i n (\frac{2 π}{l}) X .

With an unchanged speed of the automobile-robot ( $v$ ), thus, $X = v t$ . Both Eqs. (9) and (10) are then rewritten by:

11

q_{1} = q_{0} s i n ω t = q_{0} s i n (\frac{2 π v}{l}) t .

The basic length of the automobile-robot is defined by ( $l_{1} + l_{2}$ ), as shown in Fig. 1, thus, the vibration excitation at the rear tire ( $q_{2}$ ) calculated based on the vibration excitation at the front tire is expressed by:

12

q_{2} = q_{0} s i n ω (t - t^{'}) = q_{0} s i n \frac{2 π v}{l_{1} + l_{2}} (t - \frac{X}{v}) .

From the ratio of $q_{2} / q$ calculated based on Eqs. (11) and (12), the Laplace transformation $T_{q}$ of $q_{2} / q_{1}$ is then described by:

13

T_{q} = \frac{Q_{2} (s)}{Q_{1} (s)} = c o s [\frac{2 π (l_{1} + l_{2})}{l}] - i s i n [\frac{2 π (l_{1} + l_{2})}{l}] .

Eq. (13) is then used as the vibration excitation of the automobile-robot to evaluate the characteristic of the automobile-robot’s vibrations in the frequency region.

3. Simulation and analysis result

Based on the automobile-robot’s excitations using the road’s harmonic function with $q_{0} =$ 10 mm and the road’s wavelength $l =$ 8 m as well as the dynamic parameters of the automobile-robot listed in Table 1, the vibration characteristic of the automobile-robot in the frequency region under the different operation conditions is then simulated and analyzed.

Table 1Automobile-robot’s dynamic parameters

Parameters	Values	Parameters	Values	Parameters	Values
$m$ (kg)	1384	$k_{1}$ (N/m)	90880	$c_{1}$ (Ns/m)	7733
$m_{1}$ (kg)	66	$k_{2}$ (N/m)	93884	$c_{2}$ (Ns/m)	9804
$m_{2}$ (kg)	87	$k_{t 1}$ (N/m)	193211	$c_{t 1}$ (Ns/m)	2000
$I$ (kg.m²)	11632	$k_{t 2}$ (N/m)	226422	$c_{t 2}$ (Ns/m)	2000
$l_{1}$ (m)	1.35	$l_{2}$ (m)	1.604	$q_{0}$ (mm)	10

3.1. Automobile’s vibration characteristic under different stiffness of the suspension system

To evaluate the effect of stiffness parameters in the automobile-robot’s systems on the characteristic of the acceleration-frequency in the automobile-robot, three different stiffness parameters of the automobile-robot’s suspension system including $K = [80 %, 100 %, 120 %] \times {k_{1,2}, k_{t 1,2}}$ are simulated when the automobile-robot is traveling on the road surface with the harmonic function of $q_{0} =$ 10 mm and wavelength $l =$ 8 m at $v =$ 20 m/s. Results in the acceleration-frequency of the automobile-robot’s body in the vertical and pitching vibrations have been shown in Figs. 2(a) and 2(b).

Fig. 2The response of the automobile-robot body’s acceleration-frequency under different stiffness values

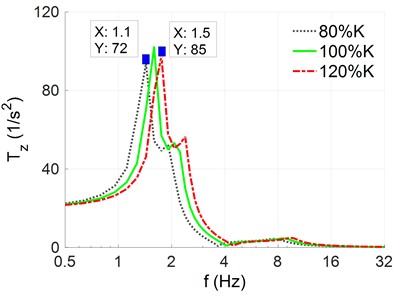
a) The vertical acceleration-frequency

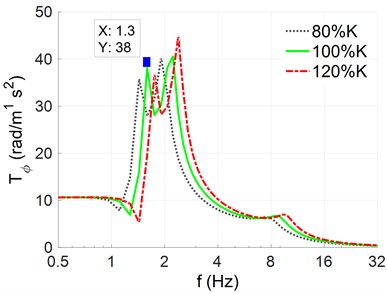
b) The pitching acceleration-frequency

The simulation results show that both the responses of the acceleration-frequency of the automobile-robot’s body in the vertical and pitching directions are significantly affected by the different stiffness coefficients of the automobile-robot’s suspensions and wheels. Resonant frequencies in the vertical and pitching direction of the automobile-robot in the low frequency region appeared at 1.1 Hz, 1.3 Hz, and 1.5 Hz when the stiffness parameters were reduced by 80 % $K$ , used by 100 % $K$ , and increased by 120 % $K$ , respectively. Additionally, the acceleration-frequency amplitude in the vertical and pitching direction of the automobile-robot at low frequencies is also depended on stiffness coefficients in the automobile-robot’s suspension systems and wheels. The automobile-robot’s acceleration-frequency amplitudes are increased with the increase of the stiffness parameters and vice versa. These results mean that the $K$ of the automobile-robot’s suspensions and wheels not only influences the amplitude but also influences the resonant-frequency of the automobile-robot’s acceleration frequency in both the vertical and pitching direction. In order to ameliorate the automobile-robot’s comfort as well as ensure the durability in automobile-robot’s structures, the designed parameters in the stiffness of automobile-robot’s suspensions and tires need to be chosen to minimum the amplitude of automobile-robot’s acceleration frequency at resonant frequencies.

3.2. Automobile’s vibration characteristic under different mass

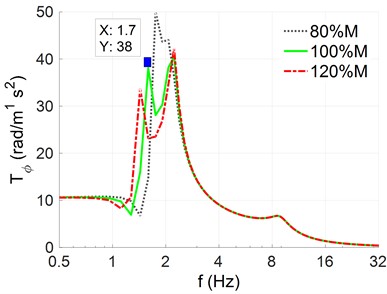
The analysis results in Section 3.1 show that the automobile-robot’s acceleration-frequency amplitudes and resonant frequencies are affected by the stiffness parameters of the automobile-robot. Besides, based on the formula used to determine the resonant frequency of the system, the resonant frequency is calculated by $f^{2} = K / M$ . Thus, the automobile-robot’s mass ( $M$ ) is also influenced the automobile-robot’s acceleration-frequency characteristic. To clearly this issue, the automobile-robot’s different mass including $M = [80 %, 100 %, 120 %] \times {m {, m}_{1}, m_{2}}$ are also simulated under the same excitation of the road surface in Section 3.1. The results of the acceleration-frequency of the automobile-robot’s body in the vertical and pitching vibrations are plotted in Figs. 3(a) and 3(b).

The simulation results indicate that both the responses of the acceleration-frequency of the automobile-robot’s body in the vertical and pitching directions are also significantly affected by the different mass in automobile-robot’s body and front/rear-axles. The resonant frequencies in the vertical and pitching direction of the automobile-robot in the low frequency region are appeared at 1.5 Hz, 1.7 Hz, and 1.9 Hz when the automobile-robot’s mass is increased by 120 % $M$ , used by 100 % $M$ , and reduced by 80 % $M$ , respectively.

Fig. 3The response of the automobile-robot body’s acceleration-frequency under different load conditions

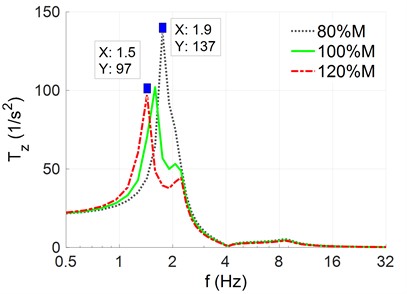
a) The vertical acceleration-frequency

b) The pitching acceleration-frequency

Besides, the amplitude of the acceleration-frequency in the vertical and pitching direction of the automobile-robot in the low frequency region is also dependent on the automobile-robot’s mass. The automobile-robot’s acceleration-frequency amplitudes are increased when the automobile-robot’s mass is reduced and vice versa. This also means that the automobile-robot’s mass not only influences amplitudes but also influence resonant-frequencies of automobile-robot’s acceleration frequency in both the vertical and pitching direction. In order to ameliorate automobile-robot’s comfort and ensure durability in automobile-robot’s structures, in the design process of the automobile-robot, both the mass $M$ and stiffness $K$ of the automobile-robot’s systems should be calculated and chosen to minimize the amplitude of the acceleration-frequency at the resonant frequencies.

3.3. Automobile’s vibration characteristic under road’s different wavelengths

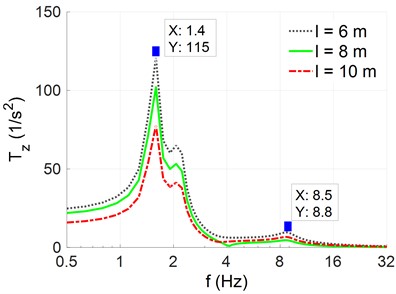
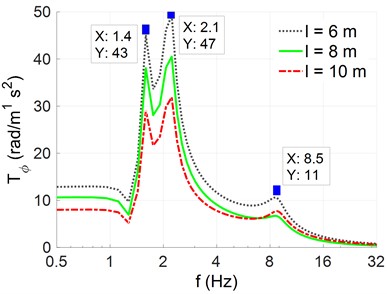
In the automobile-robot’s condition traveling on the pavement, the road wavelength can affect the automobile-robot’s ride comfort. To clear this issue, three different wavelengths of the road including $l =$ 6 m, $l =$ 8 m, and $l =$ 10 m at the same excitations of the road in Section 3.1 are simulated, respectively. The results of the acceleration-frequency of the automobile-robot’s body in the vertical and pitching vibrations are plotted in Figs. 4(a) and 4(b).

Fig. 4The response of the automobile-robot body’s acceleration-frequency under road’s different wavelengths

a) The vertical acceleration-frequency

b) The pitching acceleration-frequency

The simulation results in both Figs. 4(a) and 4(b) show that the resonant frequencies of the automobile-robot’s body in the vertical and pitching vibrations un-change and appear at 1.4 Hz, 2.1 Hz, and 8.5 Hz under the different values of the road wavelength. This means that the road wavelength not influences characteristics of the automobile-robot’s acceleration frequency. However, the amplitude of the acceleration-frequency in the vertical and pitching direction of the automobile-robot in the low frequency region is changed and affected by the road’s different wavelengths. Their amplitude is increased when the road’s wavelength is reduced and vice versa. Thus, to reduce the amplitude of the acceleration-frequency in the vertical and pitching direction of the automobile-robot, the road’s wavelength needs to be increased. This means that the pavement’s roughness needs to be decreased or the pavement’s surface quality needs to be enhanced. This issue is also proven and recommended in existing studies [20].

4. Conclusions

With automobile-robot (autonomous driving car), investigating frequency response to evaluate ride comfort and structural safety is a necessary issue. This study uses the complex-domain method for evaluating automobile-robot’s vibrations in the frequency region. The study can be summarized as follows:

The design parameters of the stiffness, mass, and road wavelength remarkably affect to characteristics of the automobile-robot’s acceleration frequency.

To reduce resonant amplitudes of the automobile-robot’s acceleration frequency in both vertical and pitching directions, stiffness parameters in the automobile-robot’s suspensions and tires should be reduced while the mass of the automobile-robot’s body should be increased. However, the reduction of the stiffness of the automobile-robot can lead to reduce the stability and safety of movement of the automobile-robot. To solve this issue, the automobile-robot’s suspension systems are researched and replaced by using air suspension systems or active suspension systems.

The resonant amplitude of the acceleration-frequency in the vertical and pitching direction of the automobile-robot is significantly affected by the road wavelength, thus, to reduce this resonant amplitude, the pavement’s roughness needs to be decreased or the pavement’s surface quality needs to be enhanced.

References

Y. Yang, W. Ren, L. Chen, M. Jiang, and Y. Yang, “Study on ride comfort of tractor with tandem suspension based on multi-body system dynamics,” Applied Mathematical Modelling, Vol. 33, No. 1, pp. 11–33, Jan. 2009, https://doi.org/10.1016/j.apm.2007.10.011

Publisher
N. Nariman-Zadeh, M. Salehpour, A. Jamali, and E. Haghgoo, “Pareto optimization of a five-degree of freedom vehicle vibration model using a multi-objective uniform-diversity genetic algorithm (MUGA),” Engineering Applications of Artificial Intelligence, Vol. 23, No. 4, pp. 543–551, Jun. 2010, https://doi.org/10.1016/j.engappai.2009.08.008

Publisher
R. Pekgökgöz, M. Gurel, M. Bilgehan, and M. Kisa, “Active suspension of cars using fuzzy logic controller optimized by genetic algorithm,” International of Journal Engineering Application Sciences, Vol. 2, No. 4, p. 27, Jul. 2010.

Search CrossRef
M. Ghoniem, T. Awad, and O. Mokhiamar, “Control of a new low-cost semi-active vehicle suspension system using artificial neural networks,” Alexandria Engineering Journal, Vol. 59, No. 5, pp. 4013–4025, Oct. 2020, https://doi.org/10.1016/j.aej.2020.07.007

Publisher
Y. Zhu, X. Bian, L. Su, C. Gu, Z. Wang, and C. Shi, “Ride comfort improvement with preview control semi-active suspension system based on supervised deep learning,” SAE International Journal of Vehicle Dynamics, Stability, and NVH, Vol. 5, No. 1, p. 31, Jan. 2021, https://doi.org/10.4271/10-05-01-0003

Publisher
H. Wang, P. Kin Wong, J. Zhao, Z.-X. Yang, and Z.-X. Yang, “Observer-based robust gain-scheduled control for semi-active air suspension systems subject to uncertainties and external disturbance,” Mechanical Systems and Signal Processing, Vol. 173, p. 109045, Jul. 2022, https://doi.org/10.1016/j.ymssp.2022.109045

Publisher
L. C. Félix-Herrán, D. Mehdi, J. J. Rodríguez-Ortiz, R. Soto, and R. Ramírez-Mendoza, “Hinf control of a suspension with a magnetorheological damper,” International Journal of Control, Vol. 85, No. 8, pp. 1026–1038, Aug. 2012, https://doi.org/10.1080/00207179.2012.674216

Publisher
I. Maciejewski, “Control system design of active seat suspensions,” Journal of Sound and Vibration, Vol. 331, No. 6, pp. 1291–1309, Mar. 2012, https://doi.org/10.1016/j.jsv.2011.11.010

Publisher
L. Wang, J. Li, Y. Yang, J. Wang, and J. Yuan, “Active control of low-frequency vibrations in ultra-precision machining with blended infinite and zero stiffness,” International Journal of Machine Tools and Manufacture, Vol. 139, pp. 64–74, Apr. 2019, https://doi.org/10.1016/j.ijmachtools.2018.11.004

Publisher
Z. Tianjun et al., “Model reference adaptive control of semi-active suspension model based on adaboost algorithm for rollover prediction,” SAE International Journal of Vehicle Dynamics, Stability, and NVH, Vol. 6, No. 1, pp. 71–86, Nov. 2021, https://doi.org/10.4271/10-06-01-0005

Publisher
“Mechanical vibration and shock-evaluation of human exposure to whole body vibration-Part 2,” Geneva, Switzerland, ISO 2631-1:1997, 1997.

Search CrossRef
“Mechanical vibration. Road surface profiles. Reporting of measured data,” Geneve, Switzerland, ISO 8068, 1995.

Search CrossRef
L. Sun, “Optimum design of “road-friendly” vehicle suspension systems subjected to rough pavement surfaces,” Applied Mathematical Modelling, Vol. 26, No. 5, pp. 635–652, May 2002, https://doi.org/10.1016/s0307-904x(01)00079-8

Publisher
X. Sun and J. Zhang, “Performance of earth-moving machinery cab with hydraulic mounts in low frequency,” Journal of Vibration and Control, Vol. 20, No. 5, pp. 724–735, Nov. 2014, https://doi.org/10.1177/10775463124642

Publisher
S. Ye et al., “Transfer path analysis and its application in low-frequency vibration reduction of steering wheel of a passenger vehicle,” Applied Acoustics, Vol. 157, p. 107021, Jan. 2020, https://doi.org/10.1016/j.apacoust.2019.107021

Publisher
M. de Brett, T. Butlin, and O. M. Nielsen, “Analysis of nonlinear vibration transmission through a vehicle suspension damper at low audio frequencies,” Journal of Sound and Vibration, Vol. 551, p. 117615, May 2023, https://doi.org/10.1016/j.jsv.2023.117615

Publisher
V. Dang, “Influence of structural parameters and operating on Vietnam’s bus ride comfort,” Hanoi University of Science and Technology, 1996.

Search CrossRef
S. D. Nguyen, Q. H. Nguyen, and S.-B. Choi, “A hybrid clustering based fuzzy structure for vibration control – Part 2: An application to semi-active vehicle seat-suspension system,” Mechanical Systems and Signal Processing, Vol. 56-57, pp. 288–301, May 2015, https://doi.org/10.1016/j.ymssp.2014.10.019

Publisher
G. Zhu et al., “A novel method to solve the existed paradox of low-frequency vibration isolation and displacement attenuation in a nonlinear floating-slab on the wheel-rail loads,” Mechanical Systems and Signal Processing, Vol. 208, p. 110985, Feb. 2024, https://doi.org/10.1016/j.ymssp.2023.110985

Publisher
J. Yang, N. van Liem, X. Wang, J. Lu, D. Shi, and C. Ma, “Performance study of semi-active seat suspension added by quasi-zero stiffness structure under various vibratory roller models,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol. 238, No. 5, pp. 1129–1143, Dec. 2022, https://doi.org/10.1177/09544070221143167

Publisher

About this article

Received

05 December 2023

Accepted

30 April 2024

Published

06 June 2024

DOI

https://doi.org/10.21595/rsa.2024.23851

Keywords

automobile-robot’s dynamic model

complex domain

ride comfort

frequency region

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

The calculation of vibration equations and simulation are performed by Jia Yujie. The analysis of the paper results is performed by Nguyen Vanliem.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 01 20

An investigation of a bus’s ride comfort by using the quarter car model with linear asymmetric damper

Dinh Duy Le, Huu Nhan Tran

Research article

2021 02 16

Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control

Yuehan Li, Vanliem Nguyen, Xiaoyan Guo, Yan Kang

Research article

2021 02 05

Research on ride comfort of vibratory rollers: Part-1 Study on the effect of different cab isolation mounts

Yan Kang, Vanliem Nguyen, Xiaoyan Guo, Yuehan Li

Research article

2020 11 26

Effect of the mass-stiffness distribution of the vibratory roller cab on the ride quality in low-frequency region

Huan Yuan, Zhiqiang Zhang, Aoran Yang, Hao Dong

Y. Jia and V. Nguyen, “Researching low frequency vibration of automobile-robot,” Robotic Systems and Applications, Vol. 4, No. 1, pp. 20–29, Jun. 2024, https://doi.org/10.21595/rsa.2024.23851

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/rsa.2024.23851
UR  - https://doi.org/10.21595/rsa.2024.23851
TI  - Researching low frequency vibration of automobile-robot
T2  - Robotic Systems and Applications
AU  - Jia, Yujie
AU  - Nguyen, Vanliem
PY  - 2024
DA  - 2024/06/06
PB  - Extrica
SP  - 20-29
VL  - 4
IS  - 1
SN  - 2669-2473
ER  - 

Copy Ris

Copied to clipboard!

 @article{Jia_2024, title={Researching low frequency vibration of automobile-robot}, ISSN={2669-2473}, url={https://doi.org/10.21595/rsa.2024.23851}, DOI={10.21595/rsa.2024.23851}, journal={Robotic Systems and Applications}, publisher={JVE International Ltd.}, author={Jia, Yujie and Nguyen, Vanliem}, year={2024}, month=jun }

Copy Bibtex

Copied to clipboard!

[1]Y. Jia and V. Nguyen, “Researching low frequency vibration of automobile-robot,” Robotic Systems and Applications, Jun. 2024, doi: 10.21595/rsa.2024.23851.

Copy IEEE

Copied to clipboard!

Jia, Yujie, and Vanliem Nguyen. “Researching Low Frequency Vibration of Automobile-Robot.” Robotic Systems and Applications, June 6, 2024. https://doi.org/10.21595/rsa.2024.23851.

Copy Chicago

Copied to clipboard!

Researching low frequency vibration of automobile-robot

Abstract

1. Introduction

2. Automobile-robot’s mathematical model

2.1. Calculating the vibration equations of the automobile-robot in the time region

2.2. Calculating the vibration equations of the automobile-robot in the frequency range

2.3. Road’s excitations on car’s wheels

3. Simulation and analysis result

3.1. Automobile’s vibration characteristic under different stiffness of the suspension system

3.2. Automobile’s vibration characteristic under different mass

3.3. Automobile’s vibration characteristic under road’s different wavelengths

4. Conclusions

References

About this article

Related Articles