Galerkin-Kantorovich variational method for solving saint venant torsion problems of rectangular bars

Ike, Charles Chinwuba

doi:10.21595/jmeacs.2024.23928

Journal of Mechanical Engineering, Automation and Control Systems

Browse Journal

Submit article

Published: 22 February 2024

Check for updates

Galerkin-Kantorovich variational method for solving saint venant torsion problems of rectangular bars

Charles Chinwuba Ike¹

¹Department of Civil Engineering, Enugu State University of Science and Technology, Agbani, 402004, Enugu State, Nigeria

Cite the article Download PDF

Article in Press

Downloads 29

Abstract

The unrestrained torsional analysis of bars is an important theme in elasticity theory, first solved by Saint-Venant using semi-inverse methods. It has been considered and solved by several others using analytical methods and numerical procedures due to the importance in the design of machine parts under torsional moments. In this paper, the Saint Venant torsion problem is solved for rectangular prismatic bars using Galerkin-Kantorovich variational method (GKVM). The work presents a detailed theoretical framework of the problem, deriving using first principles considerations the stress compatibility equation in terms of the Prandtl stress function $ϕ (x, y) .$ The derived domain equation which is required to be satisfied over the rectangular cross-sectional domain is a partial differential equation of the Poisson type. GKVM is adopted as the solution method for finding the solution to the domain equation. The unknown Prandtl stress function $ϕ (x, y)$ is assumed, following Kantorovich method to be a product of an unknown function for $f (x)$ sought to minimize the Galerkin-Kantorovich variational functional (integral) (GKVF) and a known function $(y^{2} - b^{2})$ which satisfies the boundary conditions at all boundary points in the $y$ -direction, that is, at $y = \pm b .$ The resulting GKVF is a simplified functional whose integral is a second order inhomogeneous ordinary differential equation (ODE) in $f (x)$ . The integrand is solved to find $f (x)$ leading in a full determination of the Prandtl stress function. The expression for stresses, torsional moments and torsional parameters are then found and they satisfy the boundary conditions and the domain equation. The results for the torsional moments and torsional parameters are identical to previous results obtained using double finite sine transform method (DFSTM), and analytical methods. The merit of GKVM is that it has led to the exact solution of the unrestrained torsion problems.

1. Introduction

The twisting deformation analysis of prismatic and non-prismatic bars subjected to torsional moments along the longitudinal axis is a fundamental problem in the theory of elasticity of structural bars and beams [1].

The problem is significant in the analysis and design of structural members of various shapes and cross-sectional features and in mechanical parts of machines, e.g. shafts in power trains [2-8].

The problem is one of the earliest themes in the theory of elasticity investigated by several researchers, most prominently Saint Venant who proposed the first successful solution using the semi-inverse method.

In the Saint Venant solution, the functional form of two of the three displacement components is obtained from the deformation analysis of a bar’s cross-section perpendicular to the generator axis. The remaining displacement component is determined such that the governing differential equations of elasticity and boundary conditions are satisfied.

This leads to the displacement field components as $u (y, z)$ , $v (x, z)$ and $w (x, y)$ , where $u$ and $v$ are displacement components in the bar’s cross-section and $w$ is out-of-plane displacement expressed using warping function $ψ (x, y)$ which depends on the in-plane coordinates $(x, y)$ , $u$ and $v$ are expressed using $θ$ where $θ$ is the angle of twist of the cross-section per unit length along the beam’s axis.

Closed form solutions to Saint-Venant’s torsion problems exist only for a few cross-sectional shapes, typically simple shapes bounded by surfaces with simple equations. This has necessitated the use of numerical techniques for solving the unrestrained torsion problems. Several numerical techniques have been used for the problem. They include: Finite Different Method (FDM), Finite Element Method (FEM), Finite Volume Method (FVM), Boundary Element Method (BEM) and the energy methods of Ritz, Galerkin, Rayleigh and their variants. The analytical methods that have been used are the methods of separable variables, integral transforms, eigenfunction expansions and Green functions.

Joy and Mokashi [9] and Abdelkadr et al [10] have studied the unrestrained torsional analysis of prismatic bars with non-circular cross-sections and found solutions for the stresses, and torsional rigidities which were comparable to previous solutions by other researchers.

Chen [11] successfully implemented the finite volume method for the analysis of unrestrained torsion. The stresses and torsional rigidities obtained in the study were accurate as compared with previous works in thee technical literature.

Ike [12] applied the Galerkin variational method to the analytical solutions of unrestrained torsion of prismatic bars with rectangular sections. The problem was formulated using Prandtl stress functions and the stress compatibility equation as a nonhomogeneous Laplace equation of the Poisson type. Trigonometric shape functions that exactly satisfied the boundary conditions of the problem were then used to derive the Galerkin variational equations in terms of the unknown undetermined parameters of the formulation. The minimization principle was used to find the unknown parameters, thus yielding the Prandtl stress function from which the stresses, strains, torsional moments and torsional stiffness parameters were found. Ike [12] study gave exact solutions for the stresses, torsional moments and torsional stiffness parameters.

Francu et al. [13] have used analytical method to obtain mathematical solutions for unrestrained torsion of non-circular bars with prismatic cross-sections. Their solutions yielded accurate stresses, torsional moments and torsional parameters.

Ike and Oguaghamba [14] used the double finite sine transform method (DFSTM) for the closed form analysis of unrestrained torsion of rectangular bars. The problem was expressed using Prandtl stress function as an inhomogeneous Laplace equation of the Poisson type; and the DFSTM converted the problem to an algebraic one in the transformed space. The solution was found by solving the algebraic equation and inversion to the physical domain. The solution for stresses, torsional moments and torsional parameters were found to be exact as the double transform sinusoidal kernel function satisfied all the boundary conditions.

Katsikadelis and Tsiatas [15] solved the Saint-Venant torsion problem of non-homogeneous, anisotropic, non-circular prismatic bars using the boundary element method (BEM). They formulated the problem in terms of warping function as a second order differential equation with variable parameters, subjected to generalized Neuman type boundary conditions. They solved the resulting formulation using the Analog Equation Method (AEM). In the AEM adopted the governing differential equation (GDE) solved is the Poisson’s equation subjected to a fictitious source and the boundary conditions were the same. The fictitious load is found using the BEM by expansion as a finite series of radial basis functions. The AEM adopted in their study was found to have the merits of the other boundary element methods because the discretization and the integrations were done only at the boundaries. They solved numerical examples to illustrate the accuracy and efficiency of their work.

Baksa [16] developed a mathematical solution of Saint-Venant torsion problem for circular bar with a slit; for a non-homogeneous, isotropic linear elastic bar material. The shear modulus of the bar studied is a smooth function of the radial coordinate which is a type of material non-homogeneity called functionally graded material (FGM). A power law function was used to describe the shear modulus variation with the radial coordinate. Baksa [16] considered an arbitrary power law index and obtained a closed form solution for the Prandtl’s stress function, shear stresses, torsion function and torsional rigidity. Comparison with the previous results obtained using the Finite Element Method (FEM) was used to validate the work.

Ecsedi and Baksa [17] investigated the Saint-Venant torsional analysis of cylindrical, orthotropic, homogeneous, linear elastic bar with variable shear modulus. They used an analytical method to obtain the Prandtl’s stress function, warping function, shearing stresses and torsional rigidity.

Mindlin [18] used the power series method to solve Saint-Venant torsion problems. Ecsedi [19] presented some closed form solutions for unrestrained torsion of heterogeneous cylindrical bars. Hassani and Faal [20] used a finite Fourier cosine transform method to solve unrestrained torsion problems of orthotropic bars with rectangular cross-section weakened by cracks.

Fogang [21] presented a method for solving the elastic analysis of unrestrained torsion problems of bars using Green’s theorem and the finite difference method (FDM). The solution to the Saint-Venant torsion problem reduce to the solution for a stress function that satisfies the governing differential equation of equilibrium and the boundary conditions. The FDM is an approximate numerical technique that seeks the solution of the differential equations only at discrete points in the solution domain. The governing equation is expressed in finite difference form at discrete points on the domain, thus converting the problem to an algebraic equation in terms of the values of the unknowns at the grid points. The disadvantage of the FDM is that the method gives the unknown only at the defined grid points, and not at every point on the solution region, and is thus approximate. Another disadvantage is that accurate solutions are obtained by increasing the number of grid points, thus increasing the computational efforts in the method. The main advantage is the simplicity of the FDM.

Agarana and Agboola [22] studied the unrestrained torsional problems of circular bars made of different materials. Several researchers including Romano et al [23], Brice and Picking [24], Hughes et al [25], Ecsedi [19], and Hassani and Faal [20] have used analytical and experimental techniques to study unrestrained torsion of bars.

Noor and Robertson [26] studied unrestrained torsion of bars using a variational method and a mixed formulation for heterogeneous, isotropic bars. Finite Difference Method (FDM) was used to solve the resulting differential equations of their formulations. Guendouz et al. [27] used an advanced and refined theory of one-dimensional (1D) and three dimensional (3D) beams to study unrestrained torsional analysis of composite bars with open cross-sections.

Analytical studies of unrestrained torsion of bars are still few and it is important to explore the use of more methods for analytical study of unrestrained torsion of bars.

This work uses the Galerkin-Kantorovich method to study the Saint-Venant torsion of bars with rectangular cross-section. The advantage of the Galerkin-Kantorovich method adopted is the assumption of one known basis function that satisfies the boundary condition, thus resulting in the simplification of the problem to a Galerkin functional in terms of only one unknown function of an independent space variable.

2. Theoretical framework

2.1. Assumptions

Saint-Venant theory of unrestrained torsion assumes as follows:

(i) the cross-section of the bar rotates roughly as a rigid body about an axis of twist.

(ii) the cross-section is prismatic.

(iii) the deformation is composed of (a) rotations of the cross-section about an axis passing through the center of twist, and (b) warping of the cross-section, which is constant for all the cross sections.

2.2. Displacement field

The displacement field components are:

1

u = - α y z,

2

v = α x y,

3

w = α ψ (x, y),

where $u$ , $v$ and $w$ are the displacements in the $x$ , $y$ and $z$ directions; $ψ (x, y)$ is the warping function and $α$ is the angle of rotation of the cross-section or the angle of twist per unit length.

2.3. Strains

The normal strains $ε_{x x}$ , $ε_{y y}$ , $ε_{z z}$ and shear strains $γ_{x y}$ , $γ_{y z}$ , $γ_{x z}$ are found using the small-displacement relations as:

4

ε_{x x} = \frac{\partial u}{\partial x} = 0, ε_{y y} = \frac{\partial v}{\partial y} = 0, ε_{z z} = \frac{\partial w}{\partial z} = 0,

γ_{x y} = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} = 0, γ_{y z} = \frac{\partial w}{\partial x} + \frac{\partial u}{\partial z} = α (\frac{\partial ψ}{\partial x} - y), γ_{x z} = \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z} = α (\frac{\partial ψ}{\partial y} + x) .

2.4. Stresses

The normal stresses $σ_{x x}$ , $σ_{y y}$ , $σ_{z z}$ and shear stresses $τ_{x y}$ , $τ_{y z}$ , $τ_{x z}$ are found using the stress-strain relations of linear isotropic elasticity of homogeneous bodies as:

5

σ_{x x} = σ_{y y} = σ_{z z} = 0, τ_{x y} = 0,

τ_{x z} = G γ_{x z} = G α (\frac{\partial ψ}{\partial x} - y), τ_{z y} = G γ_{z y} = G α (\frac{\partial ψ}{\partial y} + x) .

2.5. Differential equations of equilibrium

The equilibrium equations are:

6

\frac{\partial σ_{x x}}{\partial x} + \frac{\partial τ_{x y}}{\partial y} + \frac{\partial τ_{x z}}{\partial z} + f_{x} = 0,

\frac{\partial τ_{y x}}{\partial x} + \frac{\partial σ_{y y}}{\partial y} + \frac{\partial τ_{y z}}{\partial z} + f_{y} = 0,

\frac{\partial τ_{z x}}{\partial x} + \frac{\partial τ_{z y}}{\partial y} + \frac{\partial σ_{z z}}{\partial z} + f_{z} = 0,

where $f_{x}$ , $f_{y}$ , and $f_{z}$ are body force components in the $x$ , $y$ , and $z$ directions respectively.

When body forces are ignored, the equilibrium equations reduce to:

7a

\frac{\partial τ_{x z}}{\partial z} = 0,

7b

\frac{\partial τ_{y z}}{\partial z} = 0,

7c

\frac{\partial τ_{z x}}{\partial x} + \frac{\partial τ_{z y}}{\partial y} = 0 .

Integration of Eq. (7a) gives:

8a

τ_{x z} = τ_{x z} (x, y) .

Similarly, integrating Eq. (7b) gives:

8b

τ_{y z} = τ_{y z} (x, y) .

2.6. Prandtl stress function formulation of the Saint Venant torsion problem

Prandtl derived the Prandtl stress function $ϕ (x, y)$ which satisfies the differential equations of equilibrium and from which the stresses could be derived. Let $ϕ (x, y)$ be expressed in terms of $τ_{x z}$ as:

9

τ_{x z} = \frac{\partial ϕ (x, y)}{\partial y},

where $ϕ (x, y)$ is twice differentiable and continuous in $x$ , and $y$ .

The differential equation of equilibrium – Eq. (7c) – is solved to find $τ_{z y}$ as:

10

τ_{z y} = - \frac{\partial ϕ (x, y)}{\partial x} .

2.7. Stress compatibility equation

The stress compatibility equation is:

11

\frac{\partial τ_{z x}}{\partial y} - \frac{\partial τ_{z y}}{\partial x} = \frac{\partial}{\partial y} G α (\frac{\partial ψ}{\partial x} - y) - \frac{\partial}{\partial x} (G α (\frac{\partial ψ}{\partial y} + x)) = - 2 G α .

The stress compatibility equation is expressed in terms of the Prandtl stress function as:

12

\frac{\partial}{\partial y} (\frac{\partial ϕ}{\partial y}) - \frac{\partial}{\partial x} (- \frac{\partial ϕ}{\partial x}) = - 2 G α,

13

\frac{\partial^{2} ϕ}{\partial x^{2}} + \frac{\partial^{2} ϕ}{\partial y^{2}} = \nabla^{2} ϕ (x, y) = - 2 G α .

This is a Poisson equation, a non-homogeneous Laplace equation.

2.8. Torsional moment (or torque)

The torsional moment, $M_{t}$ is:

14

M_{t} = \iint (x τ_{z y} - y τ_{z x}) d x d y,

15

M_{t} = \iint x (- \frac{\partial ϕ}{\partial x}) - y (\frac{\partial ϕ}{\partial y}) d x d y,

16

M_{t} = \iint (- x \frac{\partial ϕ}{\partial x} - y \frac{\partial ϕ}{\partial y}) d x d y,

17

M_{t} = - \iint (x \frac{\partial ϕ}{\partial x} + y \frac{\partial ϕ}{\partial y}) d x d y,

18

M_{t} = - \iint (\frac{\partial}{\partial x} (x ϕ (x, y)) + \frac{\partial}{\partial y} (y ϕ (x, y))) d x d y,

19

M_{t} = - \{\int x ϕ - \int ϕ d x d y + \int y ϕ - \int ϕ d y d x\},

20

M_{t} = - \oint (ϕ x n_{x} + ϕ y n_{y}) d s + 2 \iint ϕ (x, y) d x d y .

The contour integral vanishes since $ϕ = 0$ on the contour:

21

M_{t} = 2 \iint_{R_{x y}} ϕ (x, y) d x d y .

3. Methodology

The Galerkin-Kantorovich method is presented for the Saint-Venant torsional analysis of a beam with rectangular cross sections $(2 a \times 2 b)$ as shown in Fig. 1.

Fig. 1Typical beam with rectangular cross-section considered for the study

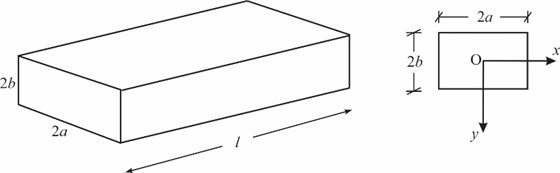
This paper considers a rectangular beam $2 a \times 2 b$ in cross-sectional dimensions as shown in Fig. 1. The origin of coordinates is chosen as shown in Figure 1 to coincide with the center of the cross-section. The governing Poisson equation to be solved using the Galerkin-Kantorovich method is shown in Eq. (13). The boundary conditions are:

22a

ϕ (x = \pm a, y) = 0,

22b

ϕ (x, y = \pm b) = 0 .

By the Galerkin-Kantorovich method, the unknown Prandtl function $ϕ (x, y)$ is considered in a variable-separable form as the products of two functions $f (x)$ which is an unknown function of $x$ coordinate only and a known function of $y$ coordinate variable which satisfies the boundary conditions at $y = \pm b .$

A suitable assumption for $ϕ (x, y)$ is thus:

23

ϕ (x, y) = f (x) (y^{2} - b^{2}) .

Since $y^{2} - b^{2}$ satisfies the boundary conditions at $y = \pm b .$

By the Galerkin procedure, the Galerkin-Kantorovich variational formulation of the Saint Venant torsion problem becomes:

24

\int_{- a}^{a} \int_{b}^{b} (\nabla^{2} f (x) (y^{2} - b^{2}) + 2 G α) (y^{2} - b^{2}) d x d y = 0 .

Eq. (24) is written explicitly as:

25

\int_{- a}^{a} \int_{b}^{b} (\frac{\partial^{2}}{\partial x^{2}} f (x) (y^{2} - b^{2}) + \frac{\partial^{2}}{\partial y^{2}} f (x) (y^{2} - b^{2}) + 2 G α) (y^{2} - b^{2}) d x d y = 0 .

Simplifying Eq. (25) gives:

26

\int_{- a}^{a} f'' (x) {(y^{2} - b^{2})}^{2} + 2 f (x) (y^{2} - b^{2}) + 2 G α (y^{2} - b^{2}) d x d y = 0 .

Further simplification of Eq. (26) gives:

27

\int_{- a}^{a} (\frac{16 b^{5}}{15} f'' (x) - \frac{8 b^{3}}{3} f (x) - \frac{8 b^{3}}{3} G α) d x = 0 .

The integral is of the general form:

28

\int_{- a}^{z} F (x, f (x), f'' (x)) d x = 0,

where:

29

F (x, f (x), f'' (x)) = \frac{16 b^{3}}{15} f'' (x) - \frac{8 b^{3}}{3} f (x) - \frac{8 b^{3}}{3} G α = 0 .

Simplifying the integrand gives:

30

f^{''} (x) - \frac{2.5}{b^{3}} f (x) = 2.5 \frac{G α}{b^{3}} .

4. Results

4.1. Homogenous solution

The homogenous solution $f_{h} (x)$ is sought in the exponential form as:

31

f_{h} (x) = e^{λ x},

where $λ$ is a parameter sought such that $f_{h} (x)$ satisfies the homogeneous equations.

By substitution of Eq. (31) in the homogeneous form of Eq. (30) gives:

32

(λ^{2} - \frac{2.5}{b^{2}}) e^{λ x} = 0 .

Thus:

33

λ = \pm \frac{\sqrt{2.5}}{b} .

Then:

34

f_{h} (x) = a_{1} e^{λ x} + a_{2} e^{- λ x},

where $a_{1}$ and $a_{2}$ are integration constants; $f_{h} (x)$ is expressed using hyperbolic functions as:

35

f_{h} (x) = c_{1} c o s h λ x + c_{2} s i n h λ x,

where $c_{1}$ and $c_{2}$ are integration constants.

4.2. Particular solutions $f_{p} (x)$

The particular solution $f_{p} (x)$ is sought such that $f_{p} (x)$ satisfies Eq. (30).

Thus:

36

{f^{''}}_{p} (x) - \frac{2.5}{b^{2}} f_{p} (x) = \frac{2.5 G α}{b^{2}} .

If ${f''}_{p} (x) = 0,$ then:

37

f_{p} (x) = - G α .

4.3. General solution $f_{g} (x)$

The general solution $f_{g} (x)$ is the sum of the homogeneous and particular solutions. Thus:

38

f_{g} (x) = c_{1} c o s h λ x + c_{2} s i n h λ x - G α .

The constants $c_{1}$ and $c_{2}$ can be found using the boundary conditions at $x = \pm a, y .$

From Eq. (22a):

39

f_{g} (x = \pm a) = 0,

40

f_{g} (x = a) = c_{1} c o s h λ a + c_{2} s i n h λ a - G α = 0,

41a

f_{g} (x = - a) = c_{1} c o s h (- λ a) + c_{2} s i n h (- λ a) - G α = 0 .

Eq. (41a) can be expressed as:

41b

c_{1} c o s h (λ a) - c_{2} s i n h (λ a) = G α .

Solving Eqs. (40) and (41) simultaneously, gives:

42

c_{1} = \frac{G α}{c o s h λ a},

43

c_{2} = 0 .

Hence, the general solutions becomes:

44

f_{g} (x) = \frac{G α}{c o s h λ a} c o s h λ x - G α,

f_{g} (x) = G α (\frac{c o s h λ x}{c o s h λ a} - 1) .

Hence, the Prandtl stress function is found as:

45

ϕ (x, y) = G α (\frac{c o s h λ x}{c o s h λ a} - 1) (y^{2} - b^{2}) .

4.4. Stresses

The stresses are found as:

46

τ_{z x} = \frac{\partial}{\partial y} ϕ (x, y) = \frac{\partial}{\partial y} G α (\frac{c o s h λ x}{c o s h λ a} - 1) (y^{2} - b^{2}) = G α (\frac{c o s h λ x}{c o s h λ a} - 1) 2 y,

47

τ_{y z} = - \frac{\partial}{\partial x} ϕ (x, y) = - \frac{\partial}{\partial x} G α (\frac{c o s h λ x}{c o s h λ a} - 1) (y^{2} - b^{2}) = - G α (\frac{λ s i n h λ x}{c o s h λ a} - 1) (y^{2} - b^{2}),

48

τ_{y z} (x, y = \pm b) = 0,

49

τ_{z y} (x = a, y) = - G α λ t a n h λ a (y^{2} - b^{2}),

50

τ_{z y} (x = a, y = 0) = - G α λ t a n h λ a (- b^{2}),

51

|τ_{z y} (x = a, y = 0)| = G α λ b^{2} t a n h \sqrt{2.5} (\frac{a}{b}) = G α \frac{\sqrt{2.5}}{b} b^{2} t a n h \sqrt{2.5} (\frac{a}{b}),

|τ_{z y} (x = a, y = 0)| = G α \sqrt{2.5} b t a n h \sqrt{2.5} (\frac{a}{b}),

52

τ_{z x} (x = \pm a, y) = 0,

53

τ_{z x} (x, y = 0) = 0,

54

τ_{z x} (x, y = b) = 2 b G α (\frac{c o s h λ x}{c o s h λ a} - 1) .

4.5. Torque or torsional moment, $M_{t}$

The torsional moment, $M_{t}$ is:

55

M_{t} = 2 \int_{- a}^{a} \int_{- b}^{b} ϕ (x, y) d x d y = \int_{- a}^{a} \int_{- b}^{b} G α (\frac{c o s h λ x}{c o s h λ a} - 1) (y^{2} - b^{2}) d x d y,

56

M_{t} = \frac{16 G α a b^{3}}{3} (1 - \frac{t a n h λ a}{λ a}) .

$M_{t}$ is expressed in the standard format as:

57

M_{t} = G α J,

where:

58

J = \frac{16 a b^{3}}{3} (1 - \frac{t a n h λ a}{λ a}),

59

J = F_{t} a b^{3} .

Then:

60

F_{t} = \frac{16}{3} (1 - \frac{t a n h λ a}{λ a}) = F_{t} (\frac{a}{b}),

61

F_{t} = \frac{16}{3} (1 - \frac{t a n h \sqrt{2.5} (\frac{a}{b})}{\sqrt{2.5} (\frac{a}{b})}),

62

\frac{M_{t}}{G α} = \frac{16}{3} (1 - \frac{t a n h \sqrt{2.5} (\frac{a}{b})}{\sqrt{2.5} (\frac{a}{b})}) .

Eq. (58) is used to generate the torsion constant $J$ for various values of $a$ and $b$ and the values are shown tabulated in Table 1, together with various values of $J$ from Timoshenko and Goodier [5]. Similarly, Eq. (61) is used to compute $F_{t} (a / b)$ for various ratios of $a / b$ and the value displayed as $k_{1}$ for a rectangular bar $2 a \times 2 b$ , where:

63

k_{1} = \frac{M_{t}}{(2 a) (2 b)^{3} α},

64

k_{1} = \frac{1}{3} (1 - \frac{t a n h \sqrt{2.5} (\frac{a}{b})}{\sqrt{2.5} (\frac{a}{b})}) .

Table 1Saint-Venant torsional stiffness for various values of the cross-sectional dimensions

Cross-section		$J = a b^{3} F_{t}$ Present study	Timoshenko and Goodier [5] (Exact)
$a$	$b$	$J = a b^{3} F_{t}$ Present study	Timoshenko and Goodier [5] (Exact)
1	1	2.23420152	2.24922043
2	1	7.30563645	7.31780011
3	1	12.62741545	12.63919901
4	1	17.96025882	17.97201565
5	1	23.29357141	23.30532665
6	1	28.62690387	28.63365902
7	1	33.96023716	33.97199231
8	1	39.29357050	39.30532565

Table 2Torsional parameters for rectangular cross-sections

$\frac{a}{b}$	$\begin{matrix} k_{1} \\ F_{t} (\frac{a}{b}) \end{matrix}$ Present study	Francu et al [13]; Ike [12, 14]
1.0	0.140	0.141
1.5	0.195	0.196
2	0.228	0.229
2.5	0.249	0.249
3	0.263	0.263
4	0.281	0.281
6	0.2982	0.299
10	0.312	0.312
$\infty$	0.333	0.333

5. Discussion

In this work, Galerkin-Kantorovich variational method has been used to solve the unrestrained torsional analysis of rectangular bars. The unrestrained torsion problem is formulated using Prandtl stress function and stress compatibility equation as an inhomogeneous Laplace equation of the Poisson type. The Kantorovich approach of using one set of basis functions that satisfy the boundary conditions in one of the coordinate directions was used in expressing the unknown Prandtl stress function in product form as the product of the known basis function and an unknown basis function $f (x)$ which is sought such that the Galerkin variational functional is minimized. The Kantorovich modification simplified the integrand in the Galerkin functional to an inhomogeneous ODE of the second order in $f (x)$ . The ODE is solved, and the boundary conditions along the x direction employed to find the integration constants. With the full determination of the Prandtl stress function, the stresses, torsional moments and torsional constants are found.

In this way, analytical results that satisfy all the boundary conditions and the domain equations are found for the Saint-Venant torsion problem. The torsional moments and torsion constants are found to be identical with previous results obtained using other methods such as Double finite sine transform method, the Galerkin method and analytical method.

6. Conclusions

The unrestrained torsional analysis of a prismatic bar expressed as a Poisson equation in terms of Prandtl stress function $ϕ (x, y)$ has been solved in this paper using Galerkin-Kantorovich variational method (GKVM). The conclusions are as follows:

1) The GKVM gave analytical solutions for $ϕ (x, y)$ that satisfies all the boundary conditions and the domain equation.

2) The GKVM converted the problem to an integral equation.

3) The expressions obtained for the shear stresses, torsional moments and torsional constants satisfy all the boundary conditions and the domain equation because they were found using $ϕ (x, y)$ which satisfies all the boundary conditions and the domain equations.

4) The results for torsional moments and torsional parameters are similar to previous results obtained using DFSTM, Galerkin variational method and analytical methods.

References

S. Erdoğan, “Determination of stresses in Vlasov beam sections,” Middle East Technical University, 2019.

Search CrossRef
H. Teimoori, R. T. Faal, and R. Das, “Saint-Venant torsion analysis of bars with rectangular cross-section and effective coating layers,” Applied Mathematics and Mechanics, Vol. 37, No. 2, pp. 237–252, Mar. 2018, https://doi.org/10.1007/s10483-016-2028-8

Publisher
H. Chen, J. Gomez, and M.-J. Pindera, “Parametric finite-volume method for Saint Venant’s torsion of arbitrarily shaped cross sections,” Composite Structures, Vol. 256, p. 113052, Jan. 2021, https://doi.org/10.1016/j.compstruct.2020.113052

Publisher
K. Darılmaz, E. Orakdöğen, and K. Girgin, “Saint-Venant torsion of arbitrarily shaped orthotropic composite or FGM sections by a hybrid finite element approach,” Acta Mechanica, Vol. 229, No. 3, pp. 1387–1398, Nov. 2017, https://doi.org/10.1007/s00707-017-2067-1

Publisher
S. P. Timoshenko and J. N. Goodier, Theory of Elasticity. New York: McGraw Hill, 1970.

Search CrossRef
A. P. Boresi, R. J. Schmidt, and O. M. Sidebottom, Advanced Mechanics of Materials. New York: John Wiley and Sons Inc., 1993.

Search CrossRef
M. H. Sadd, Elasticity: Theory, Applications and Numerics. USA: Academic Press, 2014.

Search CrossRef
A. C. Ugural and S. K. Fenster, Advanced Mechanics of Materials and Applied Elasticity. New York: Prentice Hall, 2012.

Search CrossRef
C. S. Joy and I. S. Mokashi, “A finite element method for the Saint-Venant torsion and bending problems for prismatic bars,” Computers and Structures, Vol. 135, pp. 62–72, 2014, https://doi.org/10.1016/j.comp.struct.2014.01.010

Publisher
K. Abdelkader, Z. Toufik, and B.-J. Mohamed, “Torsional stress in non-circular cross sections by the finite element method,” Advances in Mechanical Engineering, Vol. 7, No. 5, May 2015, https://doi.org/10.1177/1687814015581979

Publisher
H. Chen, “Saint Venant’s torsion by the finite-volume method,” University of Virginia, Charlottesville, 2019.

Search CrossRef
C. Ike, “Galerkin solutions for the Saint-Venant torsion of prismatic bars with rectangular cross-sections,” Advances in Modelling and Analysis A, Vol. 56, No. 1, pp. 13–20, Mar. 2019, https://doi.org/10.18280/ama_a.560103

Publisher
J. Francu, P. Navackova, and P. Janicek, “Torsion of a non-circular bar,” Engineering Mechanics, Vol. 19, No. 1, pp. 45–60, 2012.

Search CrossRef
C. C. Ike and O. A. Oguaghamba, “Double finite sine transform method for Saint-Venant torsional analysis of beams with rectangular cross-section,” in Proceedings of Sustainable Engineering and Industrial Technology Conference, pp. 290–296, 2023.

Search CrossRef
J. Katsikadelis and G. Tsiatas, “Saint-Venant torsion of non-homogeneous anisotropic bars,” Journal of Applied and Computational Mechanics, Vol. 2, No. 1, pp. 42–53, Aug. 2016, https://doi.org/10.22055/jacm.2016.12270

Publisher
A. Baksa, “Saint-Venant torsion of a functionally graded circular bar with a radial slit,” Journal of Theoretical and Applied Mechanics, Vol. 50, No. 1, pp. 83–101, Feb. 2020, https://doi.org/10.7546/jtam.50.20.01.08

Publisher
I. Ecsedi and A. Baksa, “Saint-Venant torsion of cylindrical orthotropic bar,” Archive of Applied Mechanics, Vol. 93, No. 5, pp. 2025–2032, Feb. 2023, https://doi.org/10.1007/s00419-023-02370-y

Publisher
R. D. Mindlin, “Solution of St. Venant’s torsion problem by power series,” International Journal of Solids and Structures, Vol. 11, No. 3, pp. 321–328, Mar. 1975, https://doi.org/10.1016/0020-7683(75)90071-2

Publisher
I. Ecsedi, “Some analytical solutions for Saint-Venant torsion of non-homogeneous cylindrical bars,” European Journal of Mechanics – A/ Solids, Vol. 28, No. 5, pp. 985–990, 2009.

Publisher
A. R. Hassani and R. T. Faal, “Saint Venant torsion of orthotropic bars with rectangular cross-section weakened by cracks,” International Journal of Solids and Structures, Vol. 52, pp. 165–179, 2015, https://doi.org/10.1016/ijolstr.2014.10.002

Publisher
V. Fogang, Cross-sectional analysis of beams subjected to Saint-Venant torsion using the Green’s theorem and the finite difference method. MDPI AG, 2022, https://doi.org/10.20944/preprints202203.0410.v2

Publisher
Olasunmbo Agboola, “Analysis of torsional rigidity of circular beams with different engineering materials subjected to St. Venant torsion,” International Journal of Impact Engineering, Vol. 3, No. 2, pp. 33–46, 2015.

Search CrossRef
G. Romano, A. Barretta, and R. Barretta, “On torsion and shear of Saint-Venant beams,” European Journal of Mechanics – A/Solids, Vol. 35, pp. 47–60, Sep. 2012, https://doi.org/10.1016/j.euromechsol.2012.01.007

Publisher
R. Brice and R. Pickings, “Saint-Venant torsion constant of modern precast concrete bridge girders,” PCI Journal, pp. 23–31, 2021.

Publisher
A. F. Hughes, D. C. Iles, and A. S. Malik, Design of steel beams in torsion: in accordance with Eurocodes and the UK National Annexes Steel Construction Institute (SCI). Design of steel beams in torsion: in accordance with Eurocodes and the UK National Annexes Steel Construction Institute (SCI), 2011.

Search CrossRef
A. K. Noor and K. J. Robertson, “On a mixed formulation of Saint-Venant torsion problem of nonhomogeneous anisotropic bar,” University of New South Wales, Kensington, NSW, Australia, 1971.

Search CrossRef
I. Guendouz, M. Khebizi, H. Guenfoud, M. Guenfoud, and R. El Fatmi, “Analysis of torsional bending FGM beam by 3D Saint-Venant refined theory,” Structural Engineering and Mechanics, Vol. 84, No. 3, pp. 423–435, 2022, https://doi.org/10.12989/2022.84.3.423

Publisher

About this article

Received

11 January 2024

Accepted

16 February 2024

Published

22 February 2024

DOI

https://doi.org/10.21595/jmeacs.2024.23928

Keywords

Saint-Venant torsion problem

Galerkin-Kantorovich variational method

Galerkin-Kantorovich variational functional

torsional parameter

Prandtl stress function

stress compatibility equation

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Research article

2024 02 20

Solving Saint Venant torsion problems for rectangular beams using single finite Fourier sine transform method

Charles Chinwuba Ike

Research article

2018 11 15

Variational mode decomposition: mode determination method for rotating machinery diagnosis

M. Firdaus Isham, M. Salman Leong, M. Hee Lim, Z. Asrar Ahmad

Research article

2018 03 31

Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates

Charles Chinwuba Ike, Benjamin Okwudili Mama

Research article

2018 03 31

An analytical model for determining the effect of damping on 3D natural frequency of reinforced walls

Alireza Darvishpour, Ali Ghanbari, S. A. A. Hosseini, Masoud Nekooei, Tayyebeh Darvishpour

C. C. Ike, “Galerkin-Kantorovich variational method for solving saint venant torsion problems of rectangular bars,” Journal of Mechanical Engineering, Automation and Control Systems, Vol. 5, No. 1, –12, Feb. 2024, https://doi.org/10.21595/jmeacs.2024.23928

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jmeacs.2024.23928
UR  - https://doi.org/10.21595/jmeacs.2024.23928
TI  - Galerkin-Kantorovich variational method for solving saint venant torsion problems of rectangular bars
T2  - Journal of Mechanical Engineering, Automation and Control Systems
AU  - Ike, Charles Chinwuba
PY  - 2024
DA  - 2024/02/22
PB  - Extrica
VL  - 5
IS  - 1
SN  - 2669-2600
SN  - 2669-1361
ER  - 

Copy Ris

Copied to clipboard!

 @article{Ike_2024, title={Galerkin-Kantorovich variational method for solving saint venant torsion problems of rectangular bars}, ISSN={2669-1361}, url={https://doi.org/10.21595/jmeacs.2024.23928}, DOI={10.21595/jmeacs.2024.23928}, journal={Journal of Mechanical Engineering, Automation and Control Systems}, publisher={JVE International Ltd.}, author={Ike, Charles Chinwuba}, year={2024}, month=feb }

Copy Bibtex

Copied to clipboard!

[1]C. C. Ike, “Galerkin-Kantorovich variational method for solving saint venant torsion problems of rectangular bars,” Journal of Mechanical Engineering, Automation and Control Systems, Feb. 2024, doi: 10.21595/jmeacs.2024.23928.

Copy IEEE

Copied to clipboard!

Ike, Charles Chinwuba. “Galerkin-Kantorovich Variational Method for Solving Saint Venant Torsion Problems of Rectangular Bars.” Journal of Mechanical Engineering, Automation and Control Systems, February 22, 2024. https://doi.org/10.21595/jmeacs.2024.23928.

Copy Chicago

Copied to clipboard!

Galerkin-Kantorovich variational method for solving saint venant torsion problems of rectangular bars

Abstract

1. Introduction

2. Theoretical framework

2.1. Assumptions

2.2. Displacement field

2.3. Strains

2.4. Stresses

2.5. Differential equations of equilibrium

2.6. Prandtl stress function formulation of the Saint Venant torsion problem

2.7. Stress compatibility equation

2.8. Torsional moment (or torque)

3. Methodology

4. Results

4.1. Homogenous solution

4.2. Particular solutions fpx

4.3. General solution fgx

4.4. Stresses

4.5. Torque or torsional moment, Mt

5. Discussion

6. Conclusions

References

About this article

Related Articles

4.2. Particular solutions $f_{p} (x)$

4.3. General solution $f_{g} (x)$

4.5. Torque or torsional moment, $M_{t}$