Abstract
Exciters of vibrations of the type when one vibrating mass performs impacts into two immovable supports, which are located on the opposite sides with respect to the mass, are investigated. Here because of the connection of the vibrating mass with the supports the system may have the point of equilibrium located at equal or different distances from the impacting surfaces. Also, because of the difference of coefficients of restitution of impacts the system may have symmetric or non-symmetric laws of motions of the vibrating mass. Such systems are important in pipe robots and other engineering devices. Typical results of investigation of dynamics of such systems are obtained. The presented results can be used in the process of design of systems with vibrators having two impacting pairs. Investigations are performed by using analytical as well as numerical methods (calculations are performed by C++ Builder Community Edition, Newmark constant average acceleration method is used for numerical integration of equations of motion). The obtained typical graphical relationships show symmetric as well as unsymmetric regimes of motion and enable to perform their comparison. The basic novelty of this paper is the investigation of unsymmetric regimes of motion.
1. Introduction
The purpose of the work is to create exciters of vibrations of high precision according to the laws of motions, including those of very high frequency.
Exciters of vibrations of the type when one vibrating mass performs impacts into two immovable supports, which are located on the opposite sides with respect to the mass, are investigated.
Here because of the connection of the vibrating mass with the supports the system may have the point of equilibrium located at equal or different distances from the impacting surfaces or because of the difference of coefficients of restitution of impacts the system may have symmetric or non-symmetric laws of motions of the vibrating mass.
Such systems are important in pipe robots and other engineering devices.
Typical results of investigation of dynamics of such systems are obtained. The presented results can be used in the process of design of systems with vibrators having two impacting pairs.
Resonances of nonlinear vibrating systems are investigated in [1]. Impacts are analyzed in [2]. Stabilization of vibrating systems is investigated in [3]. Impacts and vibrations are analyzed in [4]. Periodic orbits are investigated in [5]. Energy sink in a vibrating system with impacts is analyzed in [6]. Impact of a particle with a wall is investigated in [7]. Multibody system is investigated in [8]. Dynamics of a pendulum is analyzed in [9]. Piecewise linearity is investigated in [10]. Resonant zones are analyzed in [11]. Sommerfeld effect is investigated in [12]. Isolated resonances are analyzed in [13]. New mechanisms in contemporary robot engineering are presented in [14]. Vibrations in transmissions are investigated in [15]. Theory of vibro-impact systems is presented in [16]. Vibrations of robots are investigated in [17]. Vibro-impact mechanism is analyzed in [18]. Vibrating system impacting into a deformable support is investigated in [19]. Vibro-impact system with harmonic resonant excitation is analyzed in [20]. Single valued motions of the vibro-impact system are investigated in [21]. Pipe robot with impact interactions is analyzed in [22]. Impact motions in elements of manipulators and robots are investigated in [23]. Manipulators and robots excited by an external variable force through mutual impacts of their separate elements are analyzed in [24]. System with two sided impacts is investigated in [25]. Soft impacts in elements of pipe robots are analyzed in [26]. Impact motions in elements of pipe robots are investigated in [27]. Vibration drives with two impacting pairs are analyzed in [28]. Pipe robot with impacts is investigated in [29]. Two-sided soft impacts are analyzed in [30]. Vibrator with two impacting pairs is investigated in [31].
Impacts in distributed parameter systems are an important problem. Large amplitude vibrations of beams are investigated in [32]. Non-linear frequencies of beams are determined in [33]. Free vibrations of beams are analyzed in [34]. For the investigation of impact motions in beam type structures analytical as well as finite element approaches are used. In such systems wave motions because of impact interactions take place.
Vibrator with two impacting pairs when one of them is in the position of equilibrium was analyzed in [31]. This paper continues the investigations presented in the previous paper for the case when one of the impacting surfaces is not necessarily in the position of equilibrium. Thus, a more general problem is solved in this paper.
In [29] pipe robot with impacts is investigated. The investigation presented in this reference shows the importance of impact interactions for the analysis of dynamics of some types of pipe robots.
The model of the investigated vibrating system is described. Results of investigation of dynamics for typical parameters of the system are presented.
2. Model of the system with two impacting pairs
Schematic representation of the system is presented in Fig. 1. In the figure 1 and 2 denote rigid non deformable immovable supports, 3 denotes position of the mass , 4 denotes the line dividing the distance between the supports into two equal parts, 5 denotes the line of static equilibrium, denotes the deflection of the impacting mass from the position of equilibrium, denotes the coefficient of stiffness of the connection of mass with the immovable foundation, denotes the coefficient of viscous damping of the connection of mass with the immovable foundation.
When the force is acting to the mass , it can move between the supports:
and at the mass impacts into the support 1, at the mass impacts into the support 2.
By introducing the notation:
where τ is the non-dimensional time and is the dimensional time, and introducing:
where is the eigenfrequency of the system in the interval Eq. (1), the upper dot denotes differentiation with respect to the time and introducing:
the following differential equation of motion in the interval Eq. (1) is obtained:
and during the instantaneous impact according to the previous equations:
Fig. 1The investigated system
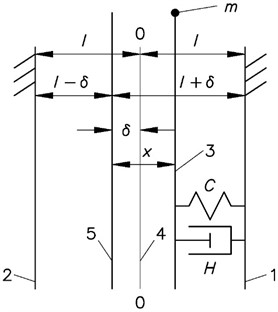
Units of measurement of the investigated quantities can be determined based on equations (4).
3. Case of the conservative system
In this case:
and the equation of motion in the interval Eq. (1) takes the form:
Here it is assumed that the first impact to support number 1 takes place, and later impact to support number 2 takes place. It can be assumed that and , where is half of a period of eigen vibrations of vibro-impact system. Two equations for the determination of period of motion are obtained:
From the obtained results it follows that:
and according to this equation graphical relationships of period of motion of the conservative system (Fig. 2) and of eigenfrequencies (Fig. 3) are obtained.
4. Investigation of separate types of exciters of vibrations
Further separate types of exciters of vibrations are analyzed.
Fig. 2x'1-l=Pτ-τ- for the following values of δ/l=0; δ/l=0.1; δ/l=0.2; δ/l=0.3
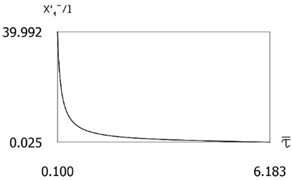
a)
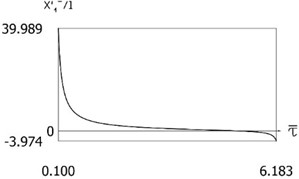
b)
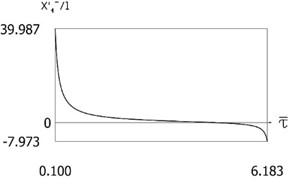
c)
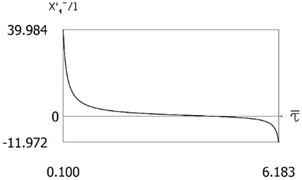
d)
Fig. 3x'1-l=Pω-ω- for the following values of δ/l=0; δ/l= 0.1; δ/l= 0.2; δ/l= 0.3
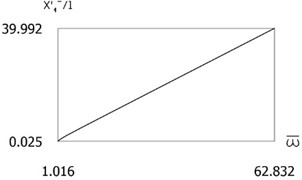
a)
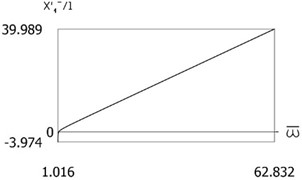
b)
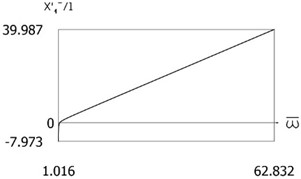
c)
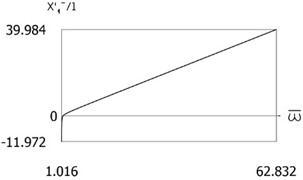
d)
The values of the parameters were chosen in the process of investigation in order to represent typical regimes of motion of the investigated system.
4.1. Case when ,
4.1.1. Conservative system
It is assumed that:
Variations of displacement as function of time and of velocity as function of time are presented in Fig. 4. The obtained results are important for comparison with the results for other values of presented further in the paper. From the presented results impacts to both impacting surfaces are seen.
Fig. 4Results of investigation of dynamics of the conservative system for l= 0.5, δ=0
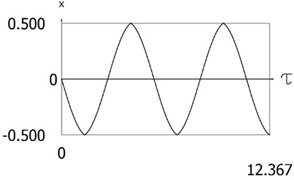
a)
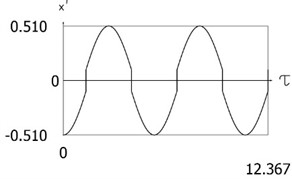
b)
4.1.2. Amplitude frequency characteristics
It is assumed that 0.5. Amplitude frequency characteristics of the displacement as well as of the velocity are presented in Fig. 5. The obtained results are important for comparison with the results for other values of presented further in the paper. From the presented results it is seen that for small amplitudes of vibrations impacts to the impacting surfaces do not take place and the system behaves as a linear one, while when the amplitude of vibrations is higher impacts to the impacting surfaces take place and thus essentially nonlinear behavior is observed. This follows directly from the character of Fig. 5.
Fig. 5Constant part and amplitudes of the first three harmonics
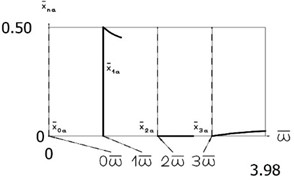
a) Displacement
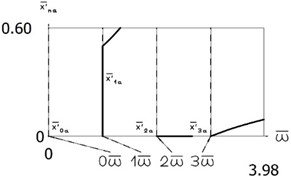
b) Velocity
4.1.3. Non conservative system
Zero initial conditions are assumed, and steady state regimes of motion are investigated.
It is assumed that:
The exciting force is denoted in the following way:
Variations of force as function of time, of displacement as function of time and of velocity as function of time are presented in Fig. 6. The obtained results are important for comparison with the results for other values of presented further in the paper. From the presented results impacts to both impacting surfaces are seen.
Fig. 6Results of investigation of dynamics for ν= 1, f= –1, h= 0.2, l= 0.5, R1= 0.7, R2= 0.7, δ= 0
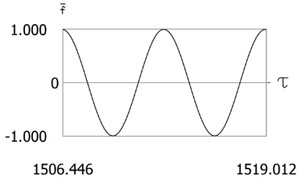
a)
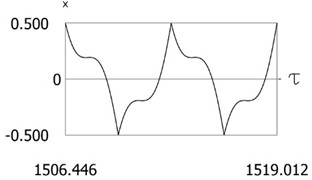
b)
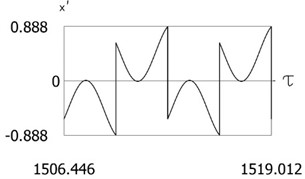
c)
4.2. Case when 0,
4.2.1. Conservative system
It is assumed that:
Variations of displacement as function of time and of velocity as function of time are presented in Fig. 7. From the obtained results and by performing the comparison with the results of the conservative system with the influence of small values of to the dynamic behavior of the investigated system is seen. From the presented results impacts to one impacting surface are seen.
4.2.2. Amplitude frequency characteristics
It is assumed that 0.5, 0.01. Amplitude frequency characteristics of the displacement as well as of the velocity are presented in Fig. 8. By performing the comparison with the results of the investigation for 0 the influence of small values of to the dynamic behavior of the investigated system is seen. From the presented results it is seen that for small amplitudes of vibrations impacts to the impacting surfaces do not take place and the system behaves as a linear one, while when the amplitude of vibrations is higher impacts to one impacting surface take place and thus essentially nonlinear behavior is observed and when the amplitude of vibrations is even more higher impacts to both impacting surfaces take place. This follows directly from the character of Fig. 8.
Fig. 7Results of investigation of dynamics of the conservative system for l= 0.5, δ= 0.01
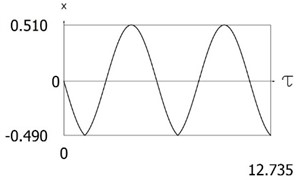
a)
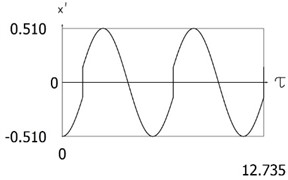
b)
Fig. 8Constant part and amplitudes of the first three harmonics
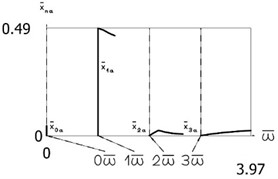
a) Displacement
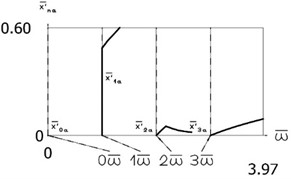
b) Velocity
4.2.3. Non conservative system
It is assumed that:
Variations of force as function of time, of displacement as function of time and of velocity as function of time are presented in Fig. 9. From the obtained results and by performing the comparison with the results of the system with 0 the influence of small values of to the dynamic behavior of the investigated system is seen. From the presented results impacts to both impacting surfaces are seen.
4.3. Case when 0,
It is assumed that:
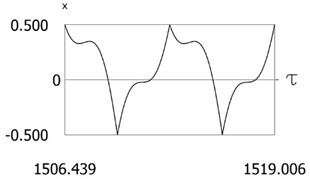
Variations of force as function of time, of displacement as function of time and of velocity as function of time are presented in Fig. 10. From the obtained results and by performing the comparison with the results of the system with mutually equal values of coefficients of restitution the influence of small changes of the values of coefficients of restitution to the dynamic behavior of the investigated system is seen. From the presented results impacts to both impacting surfaces are seen.
Fig. 9Results of investigation of dynamics for ν= 1, f= –1, h= 0.2, l= 0.5, R1= 0.7, R2= 0.7, δ= 0.01
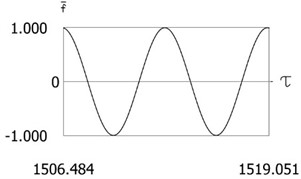
a)
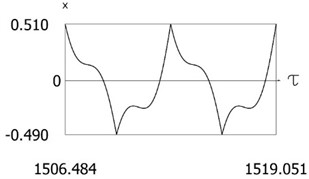
b)
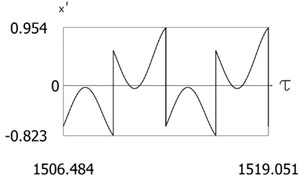
c)
Fig. 10Results of investigation of dynamics for ν= 1, f= –1, h= 0.2, l= 0.5, R1= 0.6, R2= 0.8, δ= 0
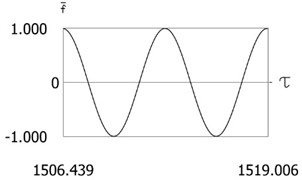
a)
b)
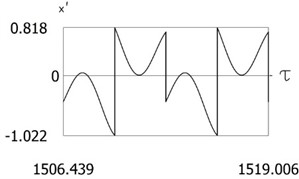
c)
4.4. Case when 0,
It is assumed that:
Variations of force as function of time, of displacement as function of time and of velocity as function of time are presented in Fig. 11.
It is assumed that:
Fig. 11Results of investigation of dynamics for ν= 1, f= –1, h= 0.2, l= 0.5, R1= 0.6, R2= 0.8, δ= 0.01
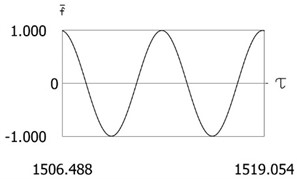
a)
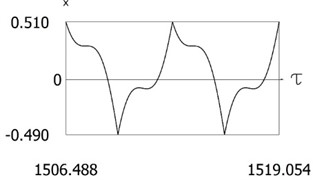
b)
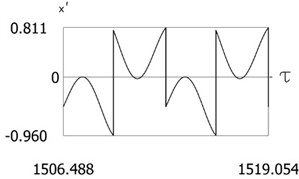
c)
Fig. 12Results of investigation of dynamics for ν= 1, f= –1, h= 0.2, l= 0.5, R1= 0.8, R2= 0.6, δ= 0.01
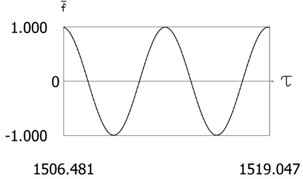
a)
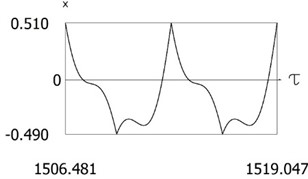
b)
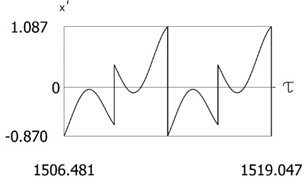
c)
Variations of force as function of time, of displacement as function of time and of velocity as function of time are presented in Fig. 12. From the obtained results and by performing the comparison with the previously obtained results the influence of small values of and small changes of the values of coefficients of restitution to the dynamic behavior of the investigated system is seen. From the presented results impacts to both impacting surfaces are seen.
5. Conclusions
Exciters of vibrations of the type when one vibrating mass performs impacts into two immovable supports, which are located on the opposite sides with respect to the mass, are investigated. Because of the connection of the vibrating mass with the supports the system may have symmetric or non-symmetric laws of motions of the vibrating mass.
Typical results of investigation of dynamics of such systems are obtained.
The effect of small changes of values of to the regimes of motion of the investigated vibro-impact system is determined. The effect of small changes of values of coefficients of restitution to the regimes of motion of the investigated vibro-impact system is determined. Finally, the effect of small changes of values of and small changes of values of coefficients of restitution to the regimes of motion of the investigated vibro-impact system is determined.
Vibrator with two impacting pairs when one of them is in the position of equilibrium was analyzed earlier. This paper continues the investigations presented in the previous paper for the case when one of the impacting surfaces is not necessarily in the position of equilibrium. Thus, a more general problem is solved in this paper.
The presented results can be used in the process of design of systems with vibrators having two impacting pairs. Such systems are important in pipe robots and other engineering devices. The purpose of the performed investigation is to create exciters of vibrations of high precision according to the laws of motions, including those of very high frequency.
The limitation of the study is in the fact that results for typical regimes of motion are obtained numerically and presented graphically, while it can be desirable to perform analytical investigations of the investigated essentially non-linear system and to obtain analytical relationships.
References
-
W. V. Wedig, “New resonances and velocity jumps in nonlinear road-vehicle dynamics,” Procedia IUTAM, Vol. 19, pp. 209–218, Jan. 2016, https://doi.org/10.1016/j.piutam.2016.03.027
-
T. Li, E. Gourc, S. Seguy, and A. Berlioz, “Dynamics of two vibro-impact nonlinear energy sinks in parallel under periodic and transient excitations,” International Journal of Non-Linear Mechanics, Vol. 90, pp. 100–110, Apr. 2017, https://doi.org/10.1016/j.ijnonlinmec.2017.01.010
-
V. A. Zaitsev, “Global asymptotic stabilization of periodic nonlinear systems with stable free dynamics,” Systems and Control Letters, Vol. 91, pp. 7–13, May 2016, https://doi.org/10.1016/j.sysconle.2016.01.004
-
H. Dankowicz and E. Fotsch, “On the analysis of chatter in mechanical systems with impacts,” Procedia IUTAM, Vol. 20, pp. 18–25, Jan. 2017, https://doi.org/10.1016/j.piutam.2017.03.004
-
S. Spedicato and G. Notarstefano, “An optimal control approach to the design of periodic orbits for mechanical systems with impacts,” Nonlinear Analysis: Hybrid Systems, Vol. 23, pp. 111–121, Feb. 2017, https://doi.org/10.1016/j.nahs.2016.08.009
-
W. Li, N. E. Wierschem, X. Li, and T. Yang, “On the energy transfer mechanism of the single-sided vibro-impact nonlinear energy sink,” Journal of Sound and Vibration, Vol. 437, pp. 166–179, Dec. 2018, https://doi.org/10.1016/j.jsv.2018.08.057
-
J. S. Marshall, “Modeling and sensitivity analysis of particle impact with a wall with integrated damping mechanisms,” Powder Technology, Vol. 339, pp. 17–24, Nov. 2018, https://doi.org/10.1016/j.powtec.2018.07.097
-
E. Salahshoor, S. Ebrahimi, and Y. Zhang, “Frequency analysis of a typical planar flexible multibody system with joint clearances,” Mechanism and Machine Theory, Vol. 126, pp. 429–456, Aug. 2018, https://doi.org/10.1016/j.mechmachtheory.2018.04.027
-
U. Starossek, “Forced response of low-frequency pendulum mechanism,” Mechanism and Machine Theory, Vol. 99, pp. 207–216, May 2016, https://doi.org/10.1016/j.mechmachtheory.2016.01.004
-
S. Wang, L. Hua, C. Yang, Y.O. Zhang, and X. Tan, “Nonlinear vibrations of a piecewise-linear quarter-car truck model by incremental harmonic balance method,” Nonlinear Dynamics, Vol. 92, No. 4, pp. 1719–1732, Feb. 2018, https://doi.org/10.1007/s11071-018-4157-6
-
P. Alevras, S. Theodossiades, and H. Rahnejat, “On the dynamics of a nonlinear energy harvester with multiple resonant zones,” Nonlinear Dynamics, Vol. 92, No. 3, pp. 1271–1286, Feb. 2018, https://doi.org/10.1007/s11071-018-4124-2
-
A. Sinha, S. K. Bharti, A. K. Samantaray, G. Chakraborty, and R. Bhattacharyya, “Sommerfeld effect in an oscillator with a reciprocating mass,” Nonlinear Dynamics, Vol. 93, No. 3, pp. 1719–1739, Apr. 2018, https://doi.org/10.1007/s11071-018-4287-x
-
G. Habib, G. I. Cirillo, and G. Kerschen, “Isolated resonances and nonlinear damping,” Nonlinear Dynamics, Vol. 93, No. 3, pp. 979–994, Apr. 2018, https://doi.org/10.1007/s11071-018-4240-z
-
Glazunov V. New mechanisms in contemporary robot engineering, Moscow: Tehnosphere, 2018.
-
Kurila R. and Ragulskienė V., Two-Dimensional Vibro-Transmissions. Vilnius: Mokslas, 1986.
-
Ragulskienė V. Vibro-shock systems (Theory and applications), Vilnius: Mintis, 1974.
-
Ragulskis K., Bansevičius R., Barauskas R., and Kulvietis G., Vibromotors for Precision Microrobots. New York: Hemisphere, 1987.
-
K. Ragulskis and L. Ragulskis, “Vibroimpact mechanism in one separate case,” Mathematical Models in Engineering, Vol. 5, No. 2, pp. 56–63, Jun. 2019, https://doi.org/10.21595/mme.2019.20818
-
K. Ragulskis and L. Ragulskis, “Dynamics of a single mass vibrating system impacting into a deformable support,” Mathematical Models in Engineering, Vol. 6, No. 1, pp. 66–78, Mar. 2020, https://doi.org/10.21595/mme.2020.21398
-
K. Ragulskis and L. Ragulskis, “Forced vibrations of vibro impact system with zero tightening with harmonic resonant excitation,” Mathematical Models in Engineering, Vol. 7, No. 1, pp. 10–21, Mar. 2021, https://doi.org/10.21595/mme.2021.21922
-
K. Ragulskis and L. Ragulskis, “Investigation of single valued motions in the vibro-impact system in case of harmonic force,” Journal of Mechanical Engineering, Automation and Control Systems, Vol. 2, No. 1, pp. 65–76, Jun. 2021, https://doi.org/10.21595/jmeacs.2021.22021
-
Ragulskis K. et al., “Investigation of dynamics of a pipe robot experiencing impact interactions,” Advances in Robotics and Automation Technology, Vol. 1, No. 2, pp. 1–8, 2021, https://doi.org/10.39127/2021/arat:1000103
-
K. Ragulskis, B. Spruogis, A. Matuliauskas, V. Mištinas, and L. Ragulskis, “Investigation of impact motions in elements of manipulators and robots,” Mathematical Models in Engineering, Vol. 7, No. 3, pp. 54–62, Sep. 2021, https://doi.org/10.21595/mme.2021.22240
-
Ragulskis K. et al., “Investigation of dynamics of manipulators and robots, the motion of which is excited by an external variable force through mutual impacts of their separate elements,” Agricultural Engineering, Vol. 53, pp. 55–62, 2021, https://doi.org/10.15544/ageng.2021.53.10
-
K. Ragulskis, A. Pauliukas, A. Bubulis, P. Paškevičius, R. Maskeliūnas, and L. Ragulskis, “Investigation of dynamics of a system with two sided impacts,” Advances in Mechanical Engineering and Transport, Vol. 1, No. 18, pp. 24–30, Jun. 2022, https://doi.org/10.36910/automash.v1i18.757
-
K. Ragulskis, B. Spruogis, M. Bogdevičius, A. Matuliauskas, V. Mištinas, and L. Ragulskis, “Investigation of soft impacts in elements of pipe robots,” Mechanics, Vol. 28, No. 5, pp. 387–393, Oct. 2022, https://doi.org/10.5755/j02.mech.29342
-
Ragulskis K. et al., “Investigation of impact motions in elements of pipe robots,” in Scientific Conference of Teaching Staff, Postgraduates, Students and Staff of Separate Structural Units of the University, Sep. 2022, https://doi.org/10.33744/2786-6459-2022-78
-
K. Ragulskis and L. Ragulskis, “Vibration drives with two impacting pairs for precise robots,” Mechanics, Vol. 29, No. 2, pp. 115–124, Apr. 2023, https://doi.org/10.5755/j02.mech.32277
-
Ragulskis K. et al., “Investigation of dynamics of the pipe robot with impacts,” in 11th International Scientific and Technical Internet – Conference Problems and Prospects of Development of Automobile Transport, 2023.
-
Ragulskis K., Pauliukas A., Paškevičius P., Maskeliūnas R., and Ragulskis L., “Investigation of two-sided soft impacts,” Advances in Mechanical Engineering and Transport, Vol. 1, No. 20, pp. 19–25, May 2023, https://doi.org/10.36910/automash.v1i20.1029
-
K. Ragulskis and L. Ragulskis, “Vibrator with two impacting pairs, one of them in the position of equilibrium,” Advanced Manufacturing Research, Vol. 1, No. 1, pp. 1–15, Jun. 2023, https://doi.org/10.21595/amr.2023.23055
-
C. Pany, “Large amplitude free vibrations analysis of prismatic and non-prismatic different tapered cantilever beams,” Pamukkale University Journal of Engineering Sciences, Vol. 29, No. 4, pp. 370–376, Jan. 2023, https://doi.org/10.5505/pajes.2022.02489
-
C. Pany and G. V. Rao, “Calculation of non-linear fundamental frequency of a cantilever beam using non-linear stiffness,” Journal of Sound and Vibration, Vol. 256, No. 4, pp. 787–790, Sep. 2002, https://doi.org/10.1006/jsvi.2001.4224
-
C. Pany and G. V. Rao, “Large amplitude free vibrations of a uniform spring-hinged beam,” Journal of Sound and Vibration, Vol. 271, No. 3-5, pp. 1163–1169, Apr. 2004, https://doi.org/10.1016/s0022-460x(03)00572-8
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Kazimieras Ragulskis: conceptualization, formal analysis, investigation, methodology, supervision, validation, visualization, writing – original draft preparation, writing – review and editing. Petras Paškevičius: formal analysis, investigation, methodology, supervision, validation, visualization, writing – original draft preparation, writing – review and editing. Liutauras Ragulskis: visualization.
The authors declare that they have no conflict of interest.
