Adaptive robust control of electromagnetic actuators with friction nonlinearity and uncertainty compensation

1. Introduction

Electromagnetic actuators have a wide range of applications of various electromagnetic damping systems in machinery [1], transportation [2], and national defense [3]. The electromagnetic actuator avoids the shortcomings of the traditional hydraulic actuator easy to leak, but also can directly convert electrical energy into mechanical energy with fast response, high efficiency, energy saving multiple advantages [4].

With the continuous improvement of the tracking performance requirements of the electromagnetic actuator in industry, how to further improve its control effect has received extensive attention from researchers. However, as a complex nonlinear system, it is not easy to reduce the effects of its inherent nonlinearity and uncertainty through the effective design of control strategies. For electromagnetic actuators in which all the information is known, feedback linearization control methods can be applied to obtain high precision control [5]. However, accurate mathematical modeling cannot completely represent all the characteristics of the actual physical model, there are always various uncertainties, including parameter uncertainty and uncertain nonlinearity. The uncertain parameters in the electromagnetic actuator can be estimated in real time by adaptive control to ensure that the system obtains asymptotic tracking performance [6-8]. Unfortunately, it is difficult for adaptive controllers to handle uncertain nonlinearities effectively. In addition, electromagnetic actuators usually drive the loads directly, and undoubtedly the existence of various uncertain nonlinearities is the main obstacle constraining the performance of adaptive control. In order to enhance the robustness of adaptive controllers, sliding mode controllers with excellent robustness performance are used to simultaneously handle the unknown parameters and unmodeled disturbances of electromagnetic actuators [9-10]. In [9], a model-free adaptive sliding mode control method solves the problems of inaccurate model and time-varying parameters of the electromagnetic actuator and obtains better dynamic performance than the traditional PID control. In addition, the excellent anti-interference effect of sliding mode control compared with state feedback control is presented in detail in [10]. In fact, sliding mode control cannot be widely adopted in engineering because of the use of discontinuous function, which leads to serious buffeting on the sliding mode surface and system instability. Meanwhile, electromagnetic actuators do not produce discontinuous driving forces to compensate for the inherent defects of sliding mode control [11]. Recently, a robust integral of the sign of the error control method has been proposed to be inspired by the design of second order sliding mode control, which can handle various uncertainties of electromagnetic actuators with continuous control input [12]. This control method is based on the strong assumption that the first and second derivatives of the model uncertainties in the system exist and are bounded. Therefore, how to design an efficient and practical controller that can handle both parameter uncertainty and unmodeled disturbance of electromagnetic actuators is still worthy of further exploration.

In addition, the effect of friction nonlinearity in electromagnetic actuators cannot be ignored. None of the nonlinear control methods mentioned above can effectively deal with the frictional nonlinearity of electromagnetic actuators. We consider the model uncertainties present in electromagnetic actuators and also look forward to addressing the friction nonlinearity on the control performance of electromagnetic actuators, since friction is to some extent the main disturbance affecting electromagnetic actuators [11, 13]. Although the importance of friction compensation has been explored for many years, there is still a great deal of research to be done because modeling nonlinear friction characteristics is a theoretically challenging problem and compensating for friction effects in controllers has practical implications [14]. In [15], an accurate modeling based on the LuGre friction model is obtained through identification, which effectively suppressed the chattering of the electromagnetic actuator and improved the tracking performance and robustness for different desired trajectories. The active compensation of nonlinear friction in the actuator of the electromagnetic suspension system is realized by combining adaptive control [16] and improved sliding mode-active disturbance rejection control [17] with the LuGre friction model. Although active compensation of friction based on the LuGre model has achieved desirable results in the servo control of electromagnetic actuators, the LuGre model has some problems in practical applications [18-19]. First, there are unknown parameters in the Stribeck function of LuGre model which need to be obtained through a lot of identification. The second is that the LuGre model becomes very stiff when the velocity of the servo system is large. Thirdly, the LuGre model is discontinuous which is difficult to satisfy the actual controller design and amplifies the sensor noise leading to limit ring oscillations. It is worth noting that the available experimental results fully illustrate that the static friction model is close enough to the real system friction [20]. Therefore, in the compensation of friction nonlinearity, it is not necessary to choose the dynamic friction model to obtain good compensation effect. By constructing an accurate and reliable static friction model, it is also of great significance in practical engineering [21].

Motivated by the above analysis, this paper adopts the friction model based on hyperbolic tangent function approximation proposed in [22] to design a continuous friction-compensated control law to deal with friction nonlinearities combined with an adaptive robust control approach to address the effects of other model uncertainties in electromagnetic actuators. The unknown parameters are updated in real time through the construction of parameter adaptive law to reduce the influence of parameter uncertainty, and other uncertainties of the system are suppressed by the nonlinear robust control law. By using model-based expectation compensation, the overall control buffeting and noise sensitivity in the application are reduced, thus further improving the tracking accuracy. The stability analysis of the closed-loop system shows that the proposed controller can guarantee the asymptotic tracking performance to deal with the parameter uncertainty and also obtain a consistent and bounded robust performance when the electromagnetic actuator is subject to parameter uncertainty and uncertain nonlinearity.

The main contributions of this paper are as follows: first, a novel continuous friction model with hyperbolic tangent function approximation is constructed to characterize the friction nonlinearity of the electromagnetic actuator, and the detrimental effects of the friction nonlinearity are accurately counteracted by feedforward compensation. Second, the adaptive technique is combined with the nonlinear robust control law to suppress the effect of uncertainty on the tracking accuracy of the system and improve the robustness of the electromagnetic actuator.

The details of this paper are organized as follows. Problem formulation and system models is presented in Chapter 2. Chapter 3 introduces the proposed controller and its theoretical results. Comparative simulation is given in Chapter 4. Chapter 5 has some conclusions.

2. Problem formulation and system models

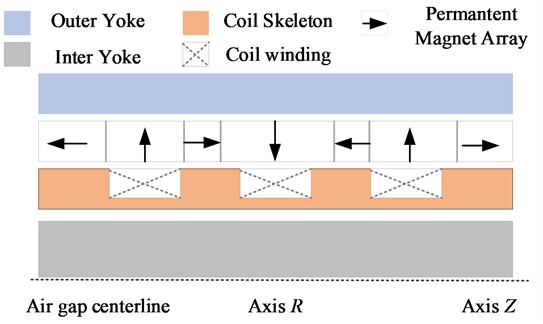
The new electromagnetic actuator uses axially magnetized permanent magnet, which is essentially a moving-coil cylindrical permanent magnet brushless DC linear motor. The structure of electromagnetic actuator considered in this paper is shown in Fig. 1 [17]. It mainly consists of permanent magnet, inner yoke, outer yoke, coil skeleton and coil, etc., in which the permanent magnet and inner and outer yokes form the stator, and the coil skeleton and coil form the actuator.

Fig. 1Structure of electromagnetic actuator

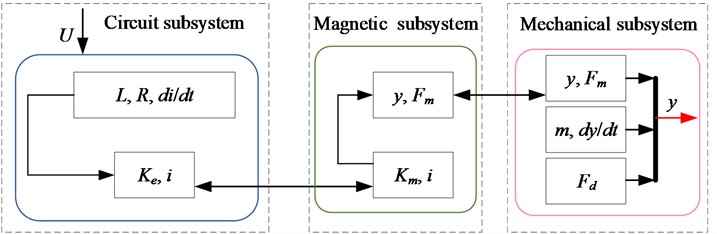
The electromagnetic actuator converts electrical energy into mechanical energy, which is a complex system of electromechanical magnetic coupling. The schematic diagram of electromagnetic actuator is presented in Fig. 2 [17]. Therefore, the dynamics of the circuit subsystem, magnetic subsystem and mechanical subsystem are modeled separately.

Fig. 2Schematic diagram of electromagnetic actuator

First, the voltage balance equation of the circuit subsystem is:

where $u$ is the phase voltage, $i$ is the phase current, $R$ is the phase resistance, $L$ is the phase inductance, $t$ is the time, $k_e$ is the back electromotive force coefficient, $v$ is the velocity of the moving actor.

Then, according to the current-carrying coil conductor in the magnetic field will be subjected to electromagnetic force, from Ampere’s law can establish the dynamics equation of the magnetic circuit subsystem as:

where $F_m$ is the electromagnetic force, $k_m$ is the electromagnetic force coefficient. In a practical electromagnetic actuator system, when $L$/$R$ is small, the derivative $di/dt$ with respect to the current tends to zero [23]. Therefore, combining Eqs. (1) and (2) yields:

Further, the dynamic equation of the mechanical subsystem based on Newton’s second law of motion is expressed as:

where $m$ is the mass of the coil assembly, $y$ is the displacement of the moving actor, $F_f$ is the friction force, $F_d$ is the lumped disturbance including unmodeled dynamics, model uncertainties, and external disturbance.

In order to more accurately describe the influence of frictional nonlinearity on electromagnetic actuators, the following continuous static friction model is adopted in this paper:

where $a_1\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(c_1\dot{y}\right)$ is coulomb friction, $a_2\left[\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(c_2\dot{y}\right)-\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(c_3\dot{y}\right)\right]$ is Stribeck effect, $a_3\dot{y}$ is viscous friction, $a_1$, $a_2$, $a_3$ denote different friction levels and $c_1$, $c_2$, $c_3$ denote various shape coefficients to approximate various friction effects.

Based on the derived dynamical model Eqs. (3), (4) and (5), define the following state variables as $x=[x_1,x_2{]}^T=[y,\dot{y}{]}^T$. Then the comprehensive dynamical model can be written in a state space form as:

The objective of the adaptive robust controller design in this paper is to construct a continuously bounded control input $u$ given the desired smooth tracking signal $x_{1d}\left(t\right)$, so that the output displacement $x_1$ of the electromagnetic actuator can accurately track the signal $x_{1d}\left(t\right)$. Before the controller derivation, there are the following realistic assumptions:

Assumption 1: The desired tracking signal $x_{1d}\left(t\right)\in C^2$ and bounded.

Assumption 2: The lumped disturbance $F_d$ is bounded, i.e. $\left|F_d\right|\le d_1$, where $d_1$ is a known positive constant.

3. Controller design

The nonlinear friction of electromagnetic actuator in practical engineering should be considered in controller design. Therefore, in order to ensure the validity and authenticity of the controller design, $\theta =[{\theta }_1,{\theta }_2,{\theta }_3{]}^T$ is defined as uncertain parameters of the friction function, in which ${\theta }_1=a_1$, ${\theta }_2=a_2$, ${\theta }_3=a_3$. Therefore, Eq. (6) can be rewritten as:

For the purpose of controller design, the following assumption about the unknown parameter set $\theta$ is made:

Assumption 3: The upper and lower bounds of the unknown parameter set $\theta$ for the friction nonlinearity of the electromagnetic actuator are known, i.e:

where ${\theta }_{\mathrm{m}\mathrm{i}\mathrm{n}}=[{\theta }_{1\mathrm{m}\mathrm{i}\mathrm{n}},{\theta }_{2\mathrm{m}\mathrm{i}\mathrm{n}},{\theta }_{3\mathrm{m}\mathrm{i}\mathrm{n}}{]}^T$ and ${\theta }_{\mathrm{m}\mathrm{a}\mathrm{x}}=[{\theta }_{1\mathrm{m}\mathrm{a}\mathrm{x}},{\theta }_{2\mathrm{m}\mathrm{a}\mathrm{x}},{\theta }_{3\mathrm{m}\mathrm{a}\mathrm{x}}{]}^T$ can be known. The definition of $\widehat{\theta }$ is the estimated value of the unknown parameter $\theta$. Let $\tilde{\theta }=\widehat{\theta }-\theta$ denotes the estimation error of the unknown parameter. In order to ensure the stability of the subsequent parameter adaptive law derivation, the following discontinuous parameter adaptive mapping function is defined based on Assumption 3 [24]:

where $i=$ 1, 2, 3, ${\cdot }_i$ represents the $i$th segment of the defining vector. Then the parametric adaptive law is constructed as follows:

with:

where $\mathrm{\Gamma }$ is a positive diagonal adaptation rate matrix, and $\tau$ is an adaptive control law; for all adaptive feedback laws $\tau$, the following properties can be ensured with Eq. (10):

Based on the above definitions and assumptions, an adaptive robust controller is designed to deal with frictional nonlinearities and lumped disturbances of electromagnetic actuator. First, define the following state variable:

where $z_1$ is the tracking error of electromagnetic actuator. The derivative of time with respect to $z_1$ is:

Next, the deviation between them is represented by characterizing $z_2\triangleq x_2-{\alpha }_1$, where ${\alpha }_1$ denotes the virtual control law of $x_2$, which can be designed as:

where $k_1$ is a positive feedback gain. Therefore, the derivative of $z_1$ can be obtained as:

Analyzing Eq. (17) reveals that $G\left(s\right)=\frac{z_1\left(s\right)}{z_2\left(s\right)}=\frac{1}{s+k_1}$ is a stable transfer function, and as $z_2$ tends to zero, $z_1$ must also tend to zero. So, the next goal of the controller design is to make $z_2$ tend to zero.

According to Eq. (7) and $z_2\triangleq x_2-{\alpha }_1$, we have:

Observing the structure of Eq. (18), the adaptive robust controller is designed by:

where $u_a$ is the adaptive model feed-forward compensation control term of the electromagnetic actuator, which can improve the stabilization accuracy of the system; $u_s$ is the robust feedback control law of the electromagnetic actuator, $u_{s1}$ is the linear robust control law used to stabilize the nominal model of the system, and $u_{s2}$ is the nonlinear robust control law used to suppress the uncertainty of the system model.

Taking Eq. (19) into (18), we have:

where $\phi =\left[\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\right(c_1{x}_2),\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}(c_2{x}_2)-\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}(c_3{x}_2),x_2{]}^T$.

In order to further improve the tracking performance of the electromagnetic actuator, design $u_{s2}$ satisfies the following stabilization conditions:

where ${\epsilon }_1$ is a positive controller parameter that can be arbitrarily small.

It is given that $h_1$ satisfies the following properties:

where ${\theta }_M={\theta }_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\theta }_{\mathrm{m}\mathrm{i}\mathrm{n}}$. Then a $u_{s2}$ design satisfying Eqs. (21) and (22) is as follows by [25]:

where $k_{s2}$ is a nonlinear control gain.

Theorem: Using the discontinuous mapping parameter adaptive law Eq. (9), the adaptive function $\tau =m^{-1}\phi z_2$ is designed and the controller gains $k_1$ and $k_2$ are chosen to be large enough such that the matrix ${\mathrm{\Lambda }}_1$ defined below is positive definite:

Then the adaptive robust controller designed in this paper for electromagnetic actuator with friction nonlinearity and model uncertainty has the following properties:

– P1: In general, all signals of a closed-loop system of electromagnetic actuators are bounded. The following Lyapunov function is defined:

Combining Eqs. (17) and (20), the derivation of $V_1$ yields:

From Eqs. (22) and (25), we have:

where $Z=[z_1^T,z_2^T{]}^T$ and $V_1$ satisfies the following inequality equation with the principle of comparison:

where ${\lambda }_1=2{\sigma }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathrm{\Lambda }}_1\right)$, and ${\sigma }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathrm{\Lambda }}_1\right)$ represents the minimum eigenvalue of ${\mathrm{\Lambda }}_1$.

Analyzing Eq. (29) shows that $V_1\in L_{\infty }$ i.e. $z_1$ and $z_2$ are also bounded. Based on assumption 1 we can get that the system states $x_1$, $x_2$ and ${\alpha }_1$ are bounded, and combining with Eq. (10), we can again know that the parameter estimate $\widehat{\theta }$ is bounded and therefore $u_a$ and $u_{s1}$ are bounded. And because $\phi$ is bounded, we finally get that the control input $u$ is bounded. This completes the proof of property P1.

– P2: When only parametric uncertainty exists in the electromagnetic actuator, i.e., the unmodeled lumped disturbance $F_d$ is 0, not only the conclusion of property P1 can be obtained, but also the asymptotic tracking performance of the electromagnetic actuator can be achieved, i.e., $Z\to 0$ as $t\to \infty$.

The following Lyapunov function is given:

Considering Eqs. (10), (17), (20) and the adaptive function $\tau =m^{-1}\phi z_2$, the derivation of $V_2$ is obtained:

Combined with Eq. (13), we have:

where $Q\in L_2$ and $V_2\in L_{\infty }$.

Because all signals of electromagnetic actuator are bounded, it can be known that $\dot{W}$ is bounded and uniformly continuous. From the lemma of Barbalat, we achieve that $Z\to 0$ as $t\to \infty$. The asymptotic stability of the electromagnetic actuator in the presence of only parametric uncertainties is obtained by stability analysis based on Lyapunov function.

4. Comparative simulation results

During the simulation, the nominal parameters of the electromagnetic actuator are $m=$ 0.2 kg, $R=$ 3.4 Ω, $k_m=$ 18 N/A, $k_e=$ 15 Vs/m, $c_1=$ 700, $c_2=$ 15, $c_3=$ 1.5, $a_1=$ 0.02, $a_2=$ 0.01, $a_3=$ 0.201. The lumped disturbance $F_d=x_1+x_2$ and the simulation sampling period is 0.5 ms. In order to verify the effectiveness of the adaptive robust control strategy for electromagnetic actuator friction compensation considering uncertainty, the following two controllers are selected for comparison in this paper.

(1) ARC: It is the proposed adaptive robust controller whose control parameters are designed as $k_1=$ 75, $k_2=$ 10, $k_{s2}=$ 2, parameter adaptation rates are given by $\mathrm{\Gamma }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{\mathrm{2,2},3\right\}$, and the initial estimate of is designed as $\widehat{\theta }\left(0\right)=[\mathrm{0,0},0{]}^T$.

(2) PID: This is a proportional-integral-differential controller widely used in engineering practice. In the comparison simulation, its controller gain is selected as: $kp=$ 50, $ki=$ 2, $kd=$ 0.5.

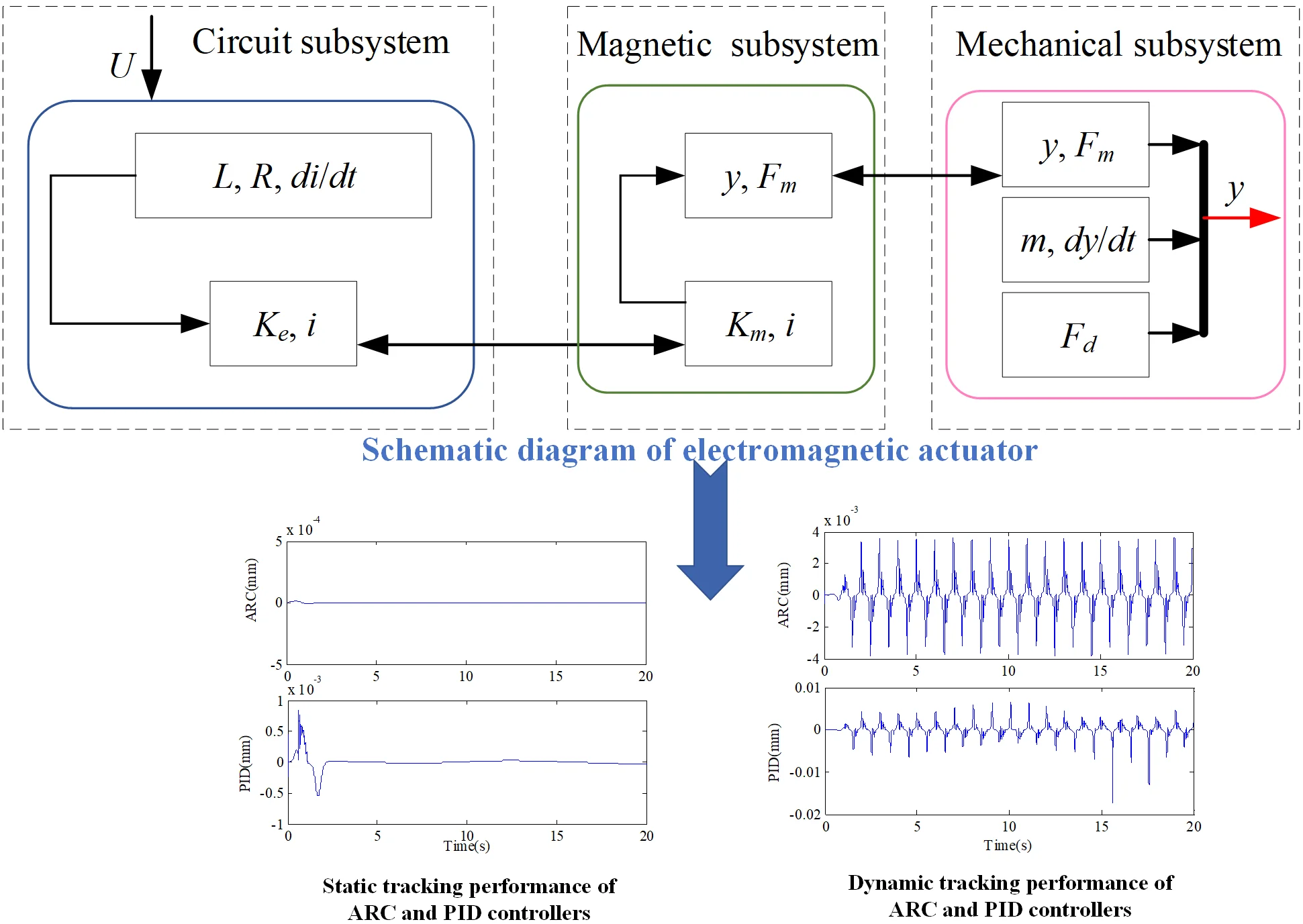
In the case 1, a smooth desired tracking trajectory $x_{1d}\left(t\right)=5(1-e^{-t^3})$ mm is chosen, which can examine the static tracking performance of the proposed control strategy on the electromagnetic actuator. The Fig. 3 shows the position tracking of the electromagnetic actuator under the action of the ARC controller, and it can be seen that the electromagnetic actuator can accurately track the given desired motion signal. The tracking error curves comparing the proposed ARC controller and the conventional PID controller is shown in Fig. 4. It is obvious from the comparison picture that the ARC controller adopts a smooth friction model to accurately compensate for the nonlinear friction of the electromagnetic actuator, and combines the nonlinear robust control law to suppress the adverse effects of the unmodeled disturbance, and thus its transient and steady state tracking performances are better than that of the conventional PID controller. The control input of the ARC control method proposed in this paper is shown in Fig. 5, which is continuously bounded.

Fig. 3Position tracking of ARC in case 1

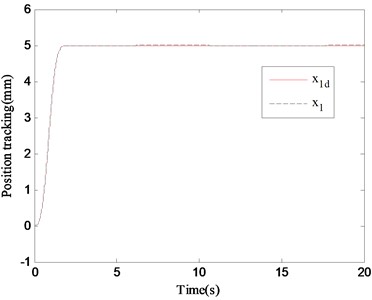
Fig. 4Tracking errors of ARC and PID in case 1

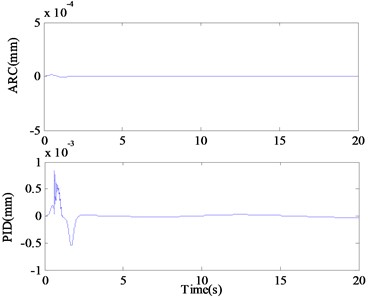
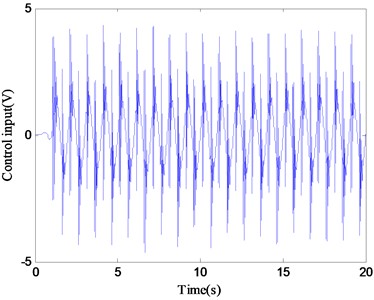
In case 2, in order to verify the dynamic tracking performance of the proposed control method, the following smooth and continuous desired tracking signal is selected in the simulation: $x_{1d}\left(t\right)=3\mathrm{s}\mathrm{i}\mathrm{n}\left(\pi t\right)(1-e^{-t^3})$ mm. Observing Fig. 6, it can be seen that the ARC controller proposed in this paper can still accurately track the desired instruction in this case. The comparative error curves of the ARC controller and the PID controller in dynamic tracking are shown in Fig. 7. The tracking performance of the proposed ARC controller is significantly better than that of the PID controller reflecting the effectiveness of the combination of adaptive robust control and continuous friction compensation. From the Fig. 8, the control input of the ARC controller is also continuously bounded in this case.

Fig. 5Control input of ARC in case 1

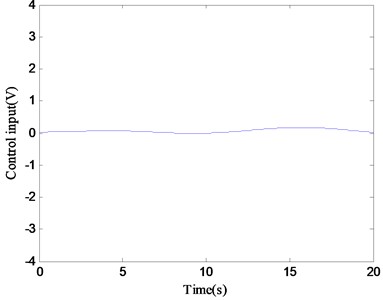
Fig. 6Position tracking of ARC in case 2

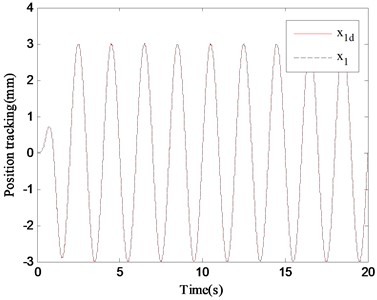
Fig. 7Tracking errors of ARC and PID in case 2

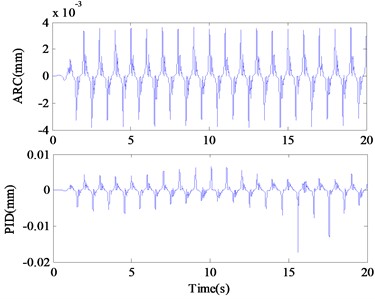
Fig. 8Control input of ARC in case 2

5. Conclusions

In this paper, we propose an adaptive robust controller that considers nonlinear friction and unmodeled disturbance for highly performance of electromagnetic actuator. Combining the adaptive approach with a continuously differentiable friction model removes the effects of friction nonlinearity through adaptive feedforward compensation. Meanwhile, a nonlinear robust feedback control law is constructed to suppress the effects of unmodeled disturbances. Stability analysis shows that asymptotic tracking can be obtained for the electromagnetic actuator with only parameter uncertainty, and the simultaneous presence of parameter uncertainty and uncertain nonlinearity also ensures that all signals of the closed-loop system in electromagnetic actuator are bounded. Multiple simulation results validate the effectiveness of the proposed adaptive robust control strategy.

The control method in this paper effectively improves the control performance of the electromagnetic actuator, but inevitably has the following limitations: first, the friction model needs to be combined with friction identification experiments to further improve the effectiveness of model compensation [26]. Secondly, in addition to the friction nonlinearity in the electromagnetic actuator there also exists the influence of discontinuous nonlinearities such as backlash nonlinearity and dead zone nonlinearity, which have not been dealt with in this paper, and subsequent research needs to pay further attention to the active compensation methods for nonlinearities such as backlash nonlinearity and dead zone nonlinearity.