Connected metric dimension of the class of ladder graphs

1. Introduction

In [1, 2], a connected resolving set of graphs was introduced recently. The shortest path between any two vertices $u,v\in V\left(G\right)$ in a linked graph $G=(V,E)$ is represented by $d(u,v)$. An ordered vertex set $B=\{x_1,x_2,...,x_k\}\subseteq V\left(G\right)$ is a metric basis of $G$ if $B$ has minimum cardinality and the following representation:

is unique for each $v\in V\left(G\right)$. A metric basis $B$ of $G$ is connected if the subgraph $\stackrel{-}{B}$ produced by $B$ is a nontrivial connected subgraph of $G$. The metric dimension and connected metric dimension of $G$, denoted as $dim\left(G\right)$ and $cdim\left(G\right)$, respectively, have the following definitions: Let $\left|B\right|$ be the cardinality of $B$, then we have: $dim\left(G\right)=min\left\{\right|Bi|:Bi\subseteq 2^v$, $Bi$ is a resolving set of $G\}$, $cdim\left(G\right)=min\left\{\right|Bi|:Bi\subseteq 2^v$, $Bi$ is a connected resolving set of $G\}$.

The connected metric dimension at a vertex $v\in V\left(G\right)$, denoted as ${cdim}_G\left(v\right)$, is the metric basis of $G$ that contains $v$ and generates a connected subgraph of $G$; then:

Slater [3, 4] introduced the concept of metric basis as a locating set of $G$ and uses the cardinality of $B$ as a locating number to locate an intruder in a network. Harary and Melter independently discovered the ideas of a metric basis as a minimum resolving set of $G$ and the cardinality of $B$ as a metric dimension [5]. A number of graphs’ metric dimensions are found in [6–15]. The following are the graphs: corona product [6], regular bipartite [7], chain graphs [8], mobius ladder [9], circulant graphs and Cayley hypergraphs [10], heptagonal circular ladder [11], generalized Petersen multigraphs [12], power of total graph [13], friendship graph [14], and quartz graph [15]. Specifically, the authors in [1] studied the linked metric dimension of the $n-1$ star network $K_1$, full graph $K_n$, cycle graph $C_n$, route graph $P_n$, and wheel graph $W_n$. The findings show that the cycle graph $C_n$, $n\ge 3$, and the route graph $P_n$, $n\ge 2$, both have connected metric dimensions that are equal to 2, whereas it is for the star graph $K_{1,n-1}$, $n\ge 4$, is $n-1$, and for the complete graph $K_n$, $n\ge 3$, is $n-1$. According to [2], the connected metric dimension of the wheel graph $W_n$, $n\ge 7$, is $⌊\frac{2n+2}{5}⌋+1$, while it is for the Petersen graph $P$ is 4, and if $v$ is an end vertex of the tree $T$, then it is at a vertex of $T$; otherwise, it is at a vertex of $T$ that is 2. Further information might be found in the literature [16-22], and some future notions may be applied to some applications like [23, 24].

To illustrate the ideas of metric dimension with its connected one, we plot in Fig. 1 the $3C_4$ –snake graph.

Fig. 13C4-Snake graph G with dim⁡G=3 and cdim⁡G=5

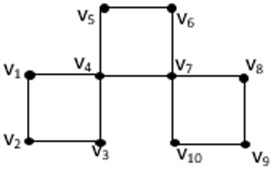
The set $B=\left\{\mathrm{}{v}_1,v_5,v_8\right\}$is a metric basis of $G$, due to the representations for the vertices of $G$ are distinct. Since the representations $r\left(v_1|B\right)=\left(\mathrm{0,2},3\right)$, $r\left(v_2|B\right)=\left(\mathrm{1,3},4\right)$, $r\left(v_3|B\right)=\left(\mathrm{2,2},3\right)$, $r\left(v_4|B\right)=\left(\mathrm{1,1},2\right)$, $r\left(v_5|B\right)=\left(\mathrm{2,0},3\right)$, $r\left(v_6|B\right)=\left(\mathrm{3,1},2\right)$, $r\left(v_7|B\right)=\left(\mathrm{2,2},1\right)$, $r\left(v_8|B\right)=\left(\mathrm{3,3},0\right)$, $r\left(v_9|B\right)=\left(\mathrm{4,4},1\right)$, $r\left(v_{10}\right|B)=(\mathrm{3,3},2)$ for the vertices of $G$ are different, the set $B=\{v_1,v_5,v_8\}$ is a metric basis of $G$. Therefore, $dim\left(G\right)=3$, and the subgraph induced by $\stackrel{-}{B}=(B,E)$ is disconnected. As a result, $B$ and $G$ are not connected resolving sets. To be more precise, no 3-element subset of $G$ is a connected resolving set. Given that the representations $r\left(v_1|\stackrel{-}{B}\right)=\left(\mathrm{0,1},\mathrm{2,2},3\right)$, $r\left(v_2|\stackrel{-}{B}\right)=\left(\mathrm{1,2},\mathrm{3,3},4\right)$, $r\left(v_3|\stackrel{-}{B}\right)=\left(\mathrm{2,1},\mathrm{2,2},3\right)\text{,}r\left(v_4|\stackrel{-}{B}\right)=\left(\mathrm{1,0},\mathrm{1,1},2\right)$, $r\left(v_5|\stackrel{-}{B}\right)=\left(\mathrm{2,1},\mathrm{0,2},3\right)$, $r\left(v_6|\stackrel{-}{B}\right)=\left(\mathrm{3,2},\mathrm{1,1},2\right)$, $r\left(v_7|\stackrel{-}{B}\right)=\left(\mathrm{2,1},\mathrm{2,0},1\right)$, $r\left(v_8|\stackrel{-}{B}\right)=\left(\mathrm{3,2},\mathrm{3,1},0\right)$, $r\left(v_9|\stackrel{-}{B}\right)=\left(\mathrm{4,3},\mathrm{4,2},1\right)$, $r\left(v_{10}\right|\stackrel{-}{B})=(\mathrm{3,2},\mathrm{3,1},2)$ are distinct, the set $\stackrel{-}{B}=\{v_1,v_4,v_5,v_7,v_8\}$ is a connected resolving set. Therefore, $cdim\left(G\right)=5$. However, we aim in this article to examine the connected metric dimension of a class of ladder graphs that includes slanting, open diagonal, triangular, open, circular, and open ladder graphs.

2. Applications of ladder graph

We present three applications pertaining to ladder graphs in this section. The three uses listed above and many more inspire us to study the uniquely elegant labelling for the ladder graph. The first application that is filed is in electronics. Resistor ladder networks are a quick and inexpensive way to do digital-to-analog conversion (DAC). The binary weighted ladder and the R/2R ladder are the two most widely used networks. Both devices can convert digital voltage information to analogue, but due to its greater accuracy and simple construction, the R/2R ladder has gained more popularity. The second application is electrical technology. The ladder flow graph is made using Ohm's equation and the two Kirchhoff equations. After that, the graph is inverted so that only forward paths are visible. The reciprocal of the total number of paths that could possibly lead from the output to the input node is the transfer function in the case of a simple ladder. If ladders with internal generators are dependent or independent, the transfer function can be found using similar methods with slight adjustments. Other relations, such as the input impedance and transfer admittance, can also be found using the flow graph. The third application is wireless communication. Over time, an increasing number of wireless networks have been developed to provide wire-free communication between any two devices (computers, phones, etc.). Nevertheless, there aren’t enough radio frequencies accessible for wireless communication (just 11 channels in the 2.4 GHz range are available for all WiFi transmissions in the US). It is essential to provide a workable manner to offer safe communications in industries like phones, mobile, security systems, WiFi, and many others [25]. It annoys me when someone else calls while I’m on the phone. This irritation is caused by interference from uncontrolled simultaneous transmissions [26]. Resonance or interference between two sufficiently adjacent channels can cause damage to communication. Interference can be prevented with the proper channel assignment. To arrive at a solution, Hale [27-30] conceptualized the problem as a graph (vertex) coloring model, which we now refer to as the $L\left(\mathrm{2,1}\right)$ coloring. Consider about the different transmitters and stations that are out there. In order to minimize interference, a channel must be assigned to each transmitter or station. Time-sensitive or error-sensitive communication may suffer from the interference phenomenon if transmitters are placed too close to one another either physically or through the frequency channels they use. To minimize interference, any two “close” transmitters ought to differ as much as possible from one another.

3. Results

Note that the two paths $P_2$ and $P_n$ are the Cartesian products of a ladder graph $L_n$.

Theorem 3.1. We have $cdim\left(L_n\right)=\frac{n}{2}$, $n\ge 4.$

Fig. 2Ladder graph Ln

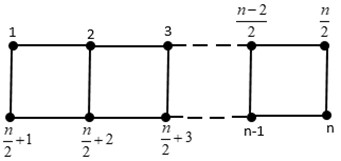
Proof. Herein, we select $\stackrel{-}{B}$ as $\stackrel{-}{B}=\left\{v_1,v_2,\dots ,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$. In this regard, we shall study each of the vertex representations of $v_i\in V\left(L_n\right)$ such that$n=2k+2$for$n\ge 4$ with respect to $\stackrel{-}{B}$. In other words, we have:

The set $\stackrel{-}{B}=\left\{v_1,v_2,..,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$ has an induced subgraph that is connected, and as previously demonstrated, the vertices in graph $L_n$ have unique representations. Despite not always being the lowest limit, this implies that $\stackrel{-}{B}$ is a connected resolving set. Therefore, $cdim\left(L_n\right)\le \frac{n}{2}$ is an upper bound. Thus, $cdim\left(L_n\right)\ge \frac{n}{2}$ is demonstrated. Given a connected resolving set $\stackrel{-}{B}=\left\{v_1,v_2,\dots ,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$, we assume that $\left|\stackrel{-}{B}\right|=\frac{n}{2}$, and ${\stackrel{-}{B}}_1$ is another minimum connected resolving set.

In the case that we choose an ordered set:

for which the two vertices $v_i$, $v_j\in L_n$ are exist so that:

This is not the case; ${\stackrel{-}{B}}_1$ is not a connected resolving set as assumed. The lowest bound is therefore $cdim\left(L_n\right)\ge \frac{n}{2}$.

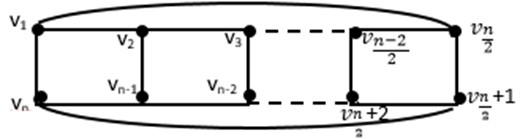
Corollary 3.2. If the ladder graph ($C\left(L_n\right)$, $n\ge 4$, $n=2k+2$, is circular, then:

Fig. 3Circular Ladder graph C(Ln)

Theorem 3.3. If the ladder graph $O\left(L_n\right)$, $n\ge 8$ is open, then $cdim\left(O\left(L_n\right)\right)=\frac{n}{2}.$

Fig. 4Open ladder graph OLn

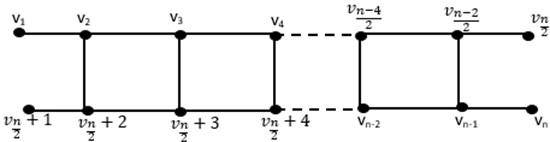
Proof. Consider we have $\stackrel{-}{B}=\left\{v_1,v_2,\dots ,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$. With respect to $\stackrel{-}{B}$, we take into consideration the following representations of vertices $v_1\in V\left(O\left(L_n\right)\right)$, $n\ge 8$, $n=2k+6$. So, we have:

Although the induced subgraph of $\stackrel{-}{B}$ is clearly connected and the representations of the vertices in graph $O\left(L_n\right)$ are different, this does not necessarily imply that $\stackrel{-}{B}$ is a connected resolving set. For this reason, $cdim\left(O\left(L_n\right)\right)\le \frac{n}{2}$ is an upper bound.

We now demonstrate that $cdim\left(O\left(L_n\right)\right)\le \frac{n}{2}$. Given a connected resolving set $\stackrel{-}{B}=\left\{v_1,v_2,\dots ,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$ with $\left|\stackrel{-}{B}\right|=\frac{n}{2}$. Let ${\stackrel{-}{B}}_1$ be an additional minimal connected resolving set. Let us choose an ordered set:

for which there are two vertices $v_i$, $v_j\in O\left(L_n\right)$ such that:

It is not the case that ${\stackrel{-}{B}}_1$ is a connected resolving set, as implied. Thus, $cdim\left(O\left(L_n\right)\right)\ge \frac{n}{2}$ is the lower bound. Ultimately, $cdim\left(O\left(L_n\right)\right)=\frac{n}{2}$.

Theorem 3.4. For $n\ge 4$, $cdim\left(T{L}_n\right)=\frac{n}{2}$ for which $G$ is a triangular ladder graph $T{L}_n$.

Fig. 5Triangular Ladder graph TLn

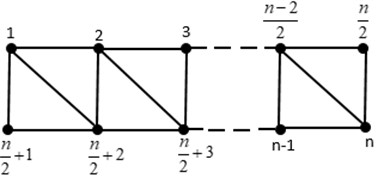
Proof. For $n\ge 4$ such that $n=2k+2$, we take into consideration a connected resolving set of ($T{L}_n$) as the set $\stackrel{-}{B}=\left\{v_1,v_2,\dots ,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$. The vertices’ representations $v_i\in V\left(T{L}_n\right)$ in connection to $\stackrel{-}{B}$ are given as follows:

The unique vertex representations in graph $T{L}_n$ suggest that $\stackrel{-}{B}$ is a connected resolving set, and as can be seen above, the induced subgraph of $\stackrel{-}{B}$ is indeed connected, but this is not always the case. Therefore, $cdim\left(T{L}_n\right)\le \frac{n}{2}$ is an upper bound. Thus, we demonstrate that $cdim\left(T{L}_n\right)\ge \frac{n}{2}$.

Given a connected resolving set $\stackrel{-}{B}=\left\{v_1,v_2,\dots ,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$, $\left|\stackrel{-}{B}\right|=\frac{n}{2}$. Let ${\stackrel{-}{B}}_1$ be an additional minimal connected resolving set. When we choose an ordered set:

Obviously, we can see that $\exists v_i$, $v_j\in T{L}_n$ for which:

It is not the case that ${\stackrel{-}{B}}_1$ is a connected resolving set, as implied. Hence, the lower bound is $cdim\left(T{L}_n\right)\ge \frac{n}{2}$. Therefore, we have $cdim\left(T{L}_n\right)=\frac{n}{2}$.

Corollary 3.5. For an open triangular ladder $O\left(T{L}_n\right)$, we have $cdim\left(O\left(T{L}_n\right)\right)=3$, $n\ge 8$.

Fig. 6Open triangular Ladder O(TLn)

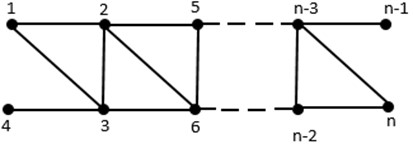
Theorem 3.6. If $S{L}_n$ is a Slanting ladder graph, then $cdim\left(S{L}_n\right)=\frac{n}{2}$, for $n\ge 6$.

Fig. 7Slanting Ladder SLn

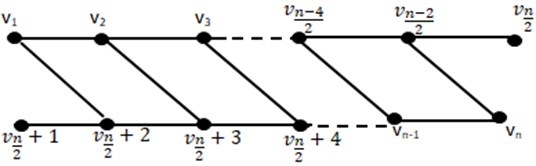
Proof. By taking into consideration $v_i\in V\left(S{L}_n\right)$ with respect to$\stackrel{-}{B}$, we assume that $\stackrel{-}{B}=\left\{v_1,v_2,\dots ,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$ is a connected resolving set for ($S{L}_n$) in which $n\ge 6$, $n=2k+4$. This implies:

The unique vertex representations in graph $S{L}_n$ suggest that $\stackrel{-}{B}$ is a connected resolving set, and as can be shown above, the induced subgraph of$\stackrel{-}{B}$ is clearly connected, but this is not always the case we desire. Because of this, $cdim\left(S{L}_n\right)\le \frac{n}{2}$ is an upper bound. Thus, we demonstrate that $cdim\left(S{L}_n\right)\ge \frac{n}{2}$.

Given a connected resolving set $\stackrel{-}{B}=\left\{v_1,v_2,..,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$, with $\left|\stackrel{-}{B}\right|=\frac{n}{2}$. Let ${\stackrel{-}{B}}_1$ be an additional minimal connected resolving set. In the event that we choose the following ordered set:

for which $\exists v_i$, $v_j\in S{L}_n$ satisfying:

It will not be a connected resolving set if, in contrast to the assumption, we choose an ordered ${\stackrel{-}{B}}_1$. As a consequence, the lower bound is $cdim\left(S{L}_n\right)\ge \frac{n}{2}$, and hence $cdim\left(S{L}_n\right)=\frac{n}{2}$.

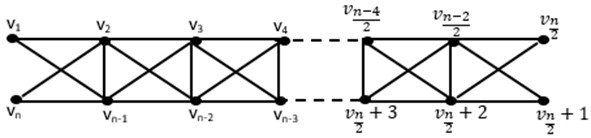
Theorem 3.7. If the graph $O\left(D{L}_n\right)$ is an open diagonal ladder, then $cdim\left(O\right(D{L}_n\left)\right)=\frac{n}{2}$, $n\ge 6$.

Proof. Take into consideration the connected resolving set of ($O\left(D{L}_n\right)$) for which $n\ge 6$, $n=2k+6$, and the set $\stackrel{-}{B}=\left\{v_1,v_2,\dots ,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$. With respect to$\stackrel{-}{B}$, consider $vi\in V\left(O\right(D{L}_n\left)\right)$ as follows:

In graph $O\left(D{L}_n\right)$, the vertex representations are unique and the induced subgraph of$\stackrel{-}{B}$ is undoubtedly connected, as can be observed above. This suggests that$\stackrel{-}{B}$ is a connected resolving set, though it need not be the lowest bound. For this reason, $cdim\left(O\right(D{L}_n\left)\right)\le \frac{n}{2}$is an upper bound, and thus we demonstrate that $cdim\left(O\right(D{L}_n\left)\right)\ge \frac{n}{2}$.

Fig. 8Open diagonal ladder graph O(DLn)

Given a connected resolving set $\stackrel{-}{B}=\left\{v_1,v_2,\dots ,v_{\frac{n-2}{2}},v_{\frac{n}{2}}\right\}$ with $\left|\stackrel{-}{B}\right|=\frac{n}{2}$. Let ${\stackrel{-}{B}}_1$ be an extra minimal connected resolving set. Assume that we choose the following ordered set:

for which $\exists v_i$, $v_j\in O\left(D{L}_n\right)$ satisfying:

It will not be a connected resolving set if, in contrast to the assumption, we choose an ordered ${\stackrel{-}{B}}_1$. As a consequence, the lower bound is $cdim\left(O\right(D{L}_n\left)\mathrm{}\right)\ge \frac{n}{2}$, and hence $cdim\left(O\left(D{L}_n\right)\mathrm{}\right)=\frac{n}{2}$.

4. Conclusions

The constant metric dimension of an open triangular ladder $O\left(T{L}_n\right)$ is 3. There are several types of ladder graphs with unbounded metric dimensions as $n\to \infty$, circular, open, triangular, slanting, and open diagonal. Our approach will be extended to ladder-class graph subdivisions in the future.