Identification of modal parameters of soil specimen based on impact force

2.1. Sample preparation

The raw material used for the sample preparation in this study is powdery clay. Six soil samples with varying compaction degrees were created by following the guidelines outlined in the “Highway Geotechnical Test Specification” (JTG3430-2020). The prepared loose soil was divided into three parts equally and loaded into the compaction cylinder in three layers, each with a fixed number of compaction. After preparation, the size of the sample was measured and recorded, and the surface was sampled to measure the actual moisture content, which corresponds to the measured water content. The samples were numbered after measurement, and the basic information about the raw materials and samples is detailed in Table 1 and Fig. 1 [13, 14].

Fig. 1Soil sample

2.2. Excitation mode and test methods

For the modal test in this experiment, the force hammer was selected as the excitation method due to convenience and practicality compared to others [15-17]. It not only allows for the application of impact force to any measurement point on the sample but also offers the flexibility to adjust the magnitude of the impact force. Additionally, the wider frequency test range of the force hammer makes it a more desirable test method for compacted soil structures with limited information. Furthermore, the soft rubber hammerhead in the experiment was chosen to minimize damage to the tested structure while meeting the required frequency range. After completing the installation of the hammerhead, the hammering test of the soil specimen commenced.

The detailed test procedure for the hammering test is as follows:

1) Measurement point labeling: the soil samples were de-molded and positioned on a fixed and clean platform, with a sponge placed between the sample and the platform to mitigate the rigid contact state. A circle was then marked on the center of the top surface of the sample, and the diameter was equivalent to half of the top diameter of the specimen. Five hammering points were evenly distributed around this circle, with the center of the circle designated as the response point for installing the acceleration sensor. The detailed locations of the response and hammering points are labeled in the sample shown in Fig. 2.

Fig. 2Hammering points and response point

2) Sensor Installation: a metal disc with a comparable contact area to the acceleration sensor was affixed with a nail at the response point for the placement of the acceleration sensor to ensure a stable signal and steady position during testing. Subsequently, connect the acceleration sensor and the force sensor of the force hammer to the signal collector to prepare for the test.

3) Pre-experiment: connect the PC with the signal collector, open the signal acquisition software, and start the pre-experiment. Hammer the desktop to ensure that the signal response of the force and acceleration sensors is normal.

4) Hammering test: The force hammer was manually operated to perform a single hammering, with the acceleration time domain signal from each hammering collected by the sensors and collector, and sent to the software system in real time, as shown in Fig. 3. During the hammering process, it is important to ensure that the direction of the hammering is perpendicular to the top surface of the sample and that the force applied is appropriate to avoid causing damage. Additionally, the hammer should be lifted quickly after each hammering to prevent secondary impacts, which could result in unwanted signals and lead to overly complex analysis. Subsequently, the same hammering is performed on each hammering point and the signal is recorded. The test is repeated three times for each sample to ensure that there are three parallel experiments at each hammering point.

Fig. 3Test equipment connection

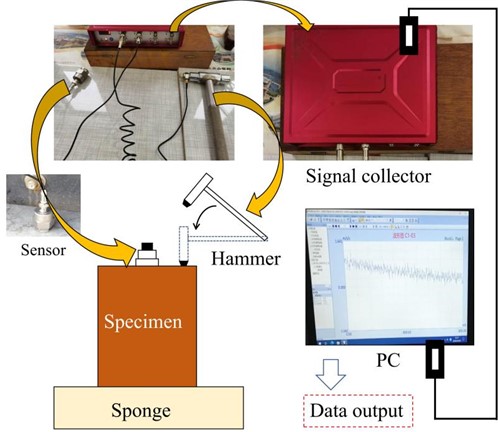
After the experiment, each sample should correspond to a total of 15 groups of test data, with 3 groups at each hammering point. Select suitable data from these three groups to carry out further research.

2.3. Test equipment

The test equipment consists of the uT85 dynamic and static strain collector, acceleration sensor, force hammer, and PC. Tables 2 and 3 present the pertinent parameters of the acquisition equipment and sensors based on the content of equipment instruction.

3.1. Displacement FRF for multi-degree-of-freedom systems

The differential equation of vibration can be expressed as Eq. (1) for an N-degree-of-freedom system [18]:

where $\left[M\right]$, $\left[C\right]$, and $\left[K\right]$ are mass, damping, and stiffness matrix, respectively; $\left\{x\right\}$, $\left\{\dot{x}\right\}$, and $\left\{\ddot{x}\right\}$ are displacement, velocity, and acceleration arrays, respectively; $\left\{f\right\}$ is the excitation force vector array. The displacement FRF of the system is:

where $r$ is the modal number, $k_r$, $m_r$, and $c_r$ are the $r$th modal stiffness, modal mass, and modal damping, respectively; ${\phi }_{lr}$ and ${\phi }_{pr}$ are the values of the modal shapes at the $l$ and $p$ point of the $r$th mode, respectively; $j$ is imaginary units; and $\omega$ is the value of the circular frequency, rad/s.

Eq. (2) reveals the relationship between the displacement FRF and the modal parameters, which is the theoretical basis for the test modal analysis. The mode of the FRF expressed by Eq. (2) is:

Eq. (3) can be further transformed as:

where, ${\xi }_r=c_r/2\sqrt{m_r{k}_r}$ is the $r$th modal damping ratio, ${\omega }_r$ is the $r$th modal circular frequency, rad/s.

Considering the modal truncation problem, it was assumed that the modes were retained up to the $G$ modes, and the higher modes above the $G$were neglected. From Eq. (4), it can be seen that the error generated by the high frequency can be approximated as a constant $D$. Therefore, Eq. (4) can be further changed to Eq. (5):

where, $K_r=k_r/{\phi }_{lr}{\phi }_{pr}$.

After the FRF was measured and the test modal number $G$ was identified, curve fitting can be performed based on Eq. (5). The results were identified as modal parameters such as the modal frequencies, damping ratios, and the residual conductance $D$ of the samples.

3.2. Measurement of FRFs

Assuming that there was no noise in the measured response signal, the measured FRF can be obtained after one measurement according to the definition based on Eq. (6):

where, $H\left(\omega \right)$ is FRF; $X\left(\omega \right)$, and $F\left(\omega \right)$ are the Fourier transforms of the displacement and force time-domain signals, respectively.

However, since the actual test will always interfere with noise, it was necessary to eliminate the effect of noise to calculate the FRF. The FRF can be estimated by Eq. (7) or (8) [19]:

where ${\widehat{H}}_1\left(\omega \right)$ and ${\widehat{H}}_2\left(\omega \right)$ are the FRFs calculated when the output and the input are noisy, respectively, and ${\widehat{G}}_{xf}\left(\omega \right)$ and ${\widehat{G}}_{fx}\left(\omega \right)$ are the mutual power spectral density functions of the excitation force signal and the displacement response time-domain signal; ${\widehat{G}}_{ff}\left(\omega \right)$ and ${\widehat{G}}_{xx}\left(\omega \right)$ are the self-power spectral density functions of the excitation force and displacement, respectively.

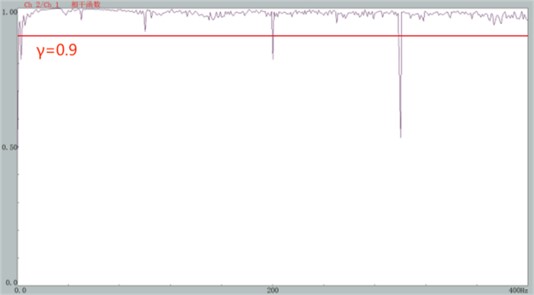
The coherence function reflects the data quality of the test results and is a basic parameter required for modal testing, and the constant coherence function of the system, ${\gamma }_{fx}\left(\omega \right)$, was calculated by Eq. (9). It is generally believed that the estimation of FRF is more accurate and reliable when ${\gamma }_{fx}\left(\omega \right)\ge 0.8$ [20]:

4.1. Modal response results and preliminary analysis

Each specimen was hammered sequentially according to the determined excitation points, and time-domain signals were obtained. The most typical test results among all were selected as a reference, as shown in Fig. 4.

Fig. 4Time domain response signal

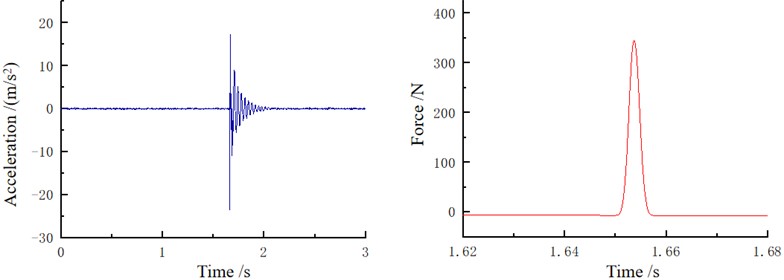
The displacement time-domain signal was first obtained by quadratic integration and then subjected to the Fast Fourier Transform (FFT). Subsequently, the estimation methods of FRF were conducted as $H_1\left(\omega \right)$ and $H_2\left(\omega \right)$ respectively, and the arithmetic mean of the two was computed to derive the final measured displacement FRF, demonstrated in Fig. 5. Each curve represents the result after averaging 5 tests. It is important to note the necessity of checking the coherence function to assess the signal quality obtained from the hammering test. The coherence functions of the data utilized must exceed 0.9 across a broad frequency band, indicating that the modal response was primarily induced by the hammering force, as shown in Fig. 6. Any data that failed to meet this criterion were excluded from subsequent analysis.

Fig. 5FRF curves

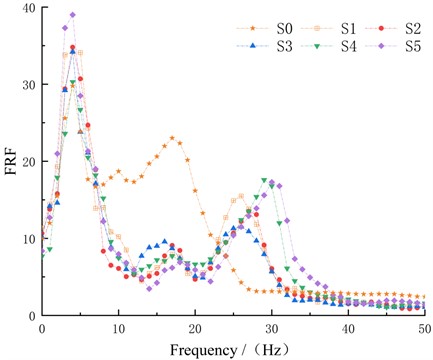
Every specimen exhibited significant 3 modes through hammering, based on Fig. 5. However, slight differences in modal amplitudes can be observed due to variations in material composition and hammering force at the excitation point. For samples S1~S5, the peaks of each mode were separated by approximately 10 Hz. The 1st modal frequency, around 4.5 Hz, displayed the highest peak value, indicating a dominant and significant amplitude-frequency characteristic. The 2nd modal frequency ranged from 15 to 20 Hz with the lowest amplitude. The 3rd modal frequency, falling between 25 and 30 Hz, was close to the recommended roller vibration frequency for compaction and exhibited the second-highest peak after the 1st modal. Notably, S0 differed from the others in terms of modal frequency location, with modes distributed within 20 Hz. This suggested significant changes in mechanical properties at the compaction level near S0 compared to higher compaction degrees, warranting further investigation of modal parameters to gain deeper insights into these variations.

Fig. 6Coherence function (the horizontal coordinate is the frequency, Hz; the vertical coordinate is the coherence function value)

4.2. Modal parameters identification

The modal parameters, including modal frequencies and damping ratios of each mode, were identified through Nonlinear Least Squares. This method adjusts the parameters of the fitting function iteratively to minimize the sum of squares of the residuals between the actual data and the fitting function. In addition, denoising the original output signal was essential before fitting to minimize the influence of noise spikes to enhance result reliability. Subsequently, utilizing Eq. (5) as a mathematical model, modal parameters were obtained via curve fitting, selecting a modal number $G=3$ for fitting based on the peak characteristics of the measured FRF. Notably, $\omega$ took values in the range [0, 50] in Eq. (5), considering the distribution interval of the modes. Meanwhile, using $1/K_r$ in Eq. (5) as the regression coefficient. This coefficient reflected the degree of contribution of each mode to the FRF, which can be visualized in Fig. 7. Furthermore, Fig. 7 illustrates the effect of fitting based on the FRF model. Table 4 presents the parameter identification result based on this fitting, including $f_r$ and ${\xi }_r$.

The standard errors (SE) and relative standard errors (RSE) of each identifiable parameter, reflecting the confidence level of the modal fitting results, are shown in Table 4. As for modal frequencies, the RSE range for the 1st to 3rd modal frequencies were 1.44 %-7.80 %, 7.58 %-13.89 %, and 3.71 %-6.71 %, respectively. The RSE of damping ratios ranged from 8.00 %-10.83 %, 10.00 %-35.00 %, and 5.00 %-12.86 %, respectively. It can be seen that the error level of the 2nd mode was relatively high due to the low intensity of the intermediate modal signal, resulting in small amplitude variations in the spectrum. More precisely, identifying it required a higher signal-to-noise ratio and finer data analysis. In contrast, the fundamental mode and the 3rd mode had more significant peak features in the spectrum, making them easier to detect and distinguish. Comparing the error levels of damping ratios and modal frequencies, the error range of modal frequencies was narrower due to the significant peak features. This indicated that modal frequencies were easier to identify and had higher accuracy compared to damping ratios, which are more susceptible to the quality of the signal.

Fig. 7The effect of fitting the FRF

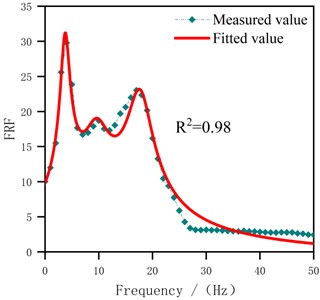
a) S0

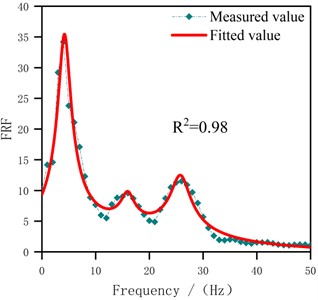
b) S1

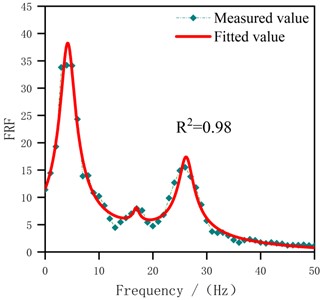
c) S2

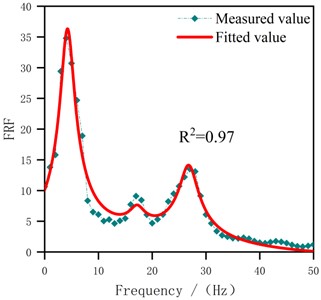
d) S3

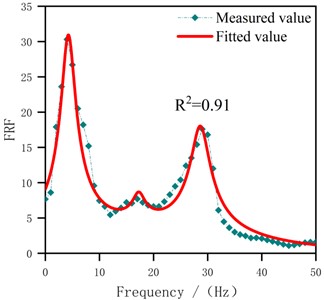
e) S4

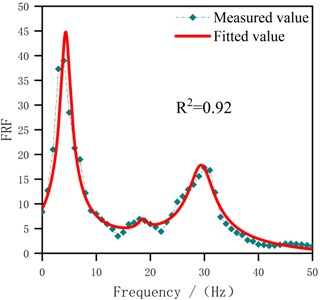
f) S5

4.3. Validity analysis of modal test methods

The dimensionless relevance between modal frequency and compaction degree was established using Table 4 data to analyze the practical value of modal parameters in road compaction operations. Referring to the variation law of modal frequency with compaction degree, the exponential and linear function models were used to fit the fundamental mode and other modes based on the least square method. The results are presented in Eqs. (10-12):

where, $f_1$, $f_2$, and $f_3$ are the 1st to 3rd modal frequencies, Hz; $f_s$ is the upper limit of frequency bandwidth, $f_s=$50 Hz of interest in here; and $\gamma$ is the compaction degree, %.

There was a significant relevance between modal frequencies and compaction degree in Table 4 at the significance level $\alpha =$0.05. Therefore, the 1st modal frequency of the sample demonstrated a growth pattern following a negative exponential function as compaction increases [21, 22]. Additionally, the 2nd and 3rd modal frequencies exhibited approximately linear increases with compaction. Notably, the 3rd modal frequency’s growth rate was significantly higher than the 2nd. This mode implied that higher modes were more sensitive to changes in the physical properties of the sample.

In addition, it can be seen that the damping ratio exhibited a significant level of variability from Table 4. Moreover, there was no strong relevance between the damping ratios of different modes and the compaction degree. This was because the damping ratio was influenced by multiple factors, not just the compactness of the soil. The damping ratio was closely related to the viscoelastic property of the compacted soil. The property may affected by particle arrangement, pore structure, and so on. These structure factors may result in different energy dissipation mechanisms at different frequencies, thereby affecting the identification of damping ratios for different modes. However, further analysis revealed that there was still a certain linear relevance mechanism between the average damping ratio of the specimens (the arithmetic mean of the damping ratios of three modes) and the compaction degree. The relevance relationship is shown in Eq. (13). There was a significant relevance at the significance level $\alpha =$0.05. This was because when calculating the average damping ratio, the damping ratios of modes 1 to 3 are comprehensively considered, thereby reducing the influence of individual damping ratios by other factors and overall presenting a linear relevance with compaction degree:

where the $\xi$ is the average damping ratio.

The above statistical analyses show that the sample modal testing method was established and the results of modal parameter identification are reliable.

4.4. Discussion

The mechanical indicators of compacted soil samples, specifically the natural frequencies and average damping ratios involved in this study, exhibit a strong liner and nonlinear relevance with the compaction degree of the samples. This suggests that the modal parameters expressed in the soil structure's vibration can effectively reflect the compaction quality. Regarding the application of the modal parameters and analysis results, in conjunction with the existing frequency range of compaction equipment (29-75 Hz), modal frequencies and average damping ratios can serve as significant references for developing compaction and quality control technologies. For instance, loose soils often require stronger agitation to achieve rapid compaction within a short time in the initial stages of compaction operations. Therefore, pre-experimental compaction operations can be prioritized on test road sections to actively apply vibration loads, collect vibration responses under different compaction states, and analyze them to identify the modal frequency ranges of the soil layer at various compaction levels. Additionally, attention should be given to the variation pattern of the first modal frequency to determine the attenuation level of growth rate and the numerical range of average damping ratio when compaction operations are completed (the use of “attenuation level” and “numerical range” is intended to take into account the fact that constant data will be difficult to obtain due to the many complex factors of field testing). During compaction operations, selecting suitable compactors (within the modal frequency range close to the compacted soil) for compaction work is recommended. Subsequently, when compaction operations reach or approach the ideal state, vibrating compactors or static compaction methods, which operate away from the modal frequency range, can be employed to complete finishing operations and avoid over-compaction. In summary, valuable insights can be provided for the improvement of compaction techniques by exploring the regularities of the mechanical indicators of compacted soil structure. It is important to note that in addition to the regularity of internal responses of soil structures, the form of external excitation also influences experimental results.

This study primarily collects and analyzes the dynamic responses of compacted soil structures by actively applying excitation, with the form of impact loads. Due to the convenience of impact load, numerous devices based on impact are based on impact for quality inspection of road structures, such as FWD, DCP, etc., most of which detect the bearing capacity of roads by detecting their physical deformations. The method proposed in this study is also based on the vibration response caused by impact load. However, this study focuses more on vibration rather than deformation. Vibration, as the most common motion pattern in nature, can reflect the level of a structure's resistance to external influences. However, this resistance cannot be directly discerned solely by the characteristics of the vibration waveform surface, hence the need to describe it by extracting parameters from the vibration response mode. Generally, it isn't easy to exhibit a single mode even under compaction, resulting in numerous modes due to the soil's inherent granular characteristics. Therefore, this study seeks feasible mechanical indicators through relevance analysis between relevant parameters and the most traditional compaction quality indicator, compaction degree. Although traditional quality inspection methods based on impact loads provide a more intuitive reflection of structural strength, significant deformation does not necessarily indicate the low load-bearing capacity of the structure. Therefore, further development is required for current compaction and quality inspection techniques to meet the demands for accuracy and efficiency in the era of intelligent compaction. Furthermore, guided by traditional physical indicators, obtaining the modal dynamic indicators of road structures and systematically monitoring the quality changes during road compaction processes should be one of the key research directions in road engineering. Additionally, experimental exploration should be prioritized indoors before the dynamic modal experiment of large-scale structures, which is also emphasized in this study.

The test method for modal parameters of cylindrical samples represents an exploratory endeavor in modal testing of indoor sample systems, with the potential for further enhancement. This is owing to the impact of factors such as shape, size, supporting and contact conditions, which influence the modal characteristics and parameters of a sample [23, 24]. Moreover, modal parameters for the same structure under different boundary conditions may vary. Consequently, the modal parameters obtained using this method may not align closely with results from field-measured roadbeds with similar soil quality and compaction. Meanwhile, the choice of incentive methods still requires further comparative research. Although the convenience of hammering as an incentive cannot be denied, the stability in stimulating the modalities of large-volume structures is uncertain. Notably, comparative analysis with field results has not been conducted due to limitations. Hence, the need for potential improvements in the indoor testing method is a pressing issue to address.