The effect of the impact of the transport load on the strength and deformability of the soil base of the road structure

1. Introduction

The design of highways that meet the most modern requirements is associated with comprehensive studies of the strength and deformability of road embankments under static and dynamic loads [1]. All the main elements of the road structure work in close cooperation and interdependence from each other; the malfunction of one element adversely affects the condition and operation of others. Therefore, in order to ensure the normal operation of the road as a whole throughout its operation, the strength and deformability of the roadbed of road embankments is of great importance [2]. When determining the strength parameters by shear tests, the actual conditions of possible displacement of the structure are displayed to the greatest extent, the phenomena of violation of soil shear resistance are obvious, visual and convincing. These experiments are extremely simple, and if the drainage conditions are met, the test data of clay soils using the direct cut method coincide with the data of three-axis compression tests. Meanwhile, these experiments have a clear advantage over triaxial compression experiments in terms of the certainty of the stress state of the sample, simplicity and reliability of strain measurement, etc. When analyzing deformation, both the geometric and physical properties of the materials of the structural layers and the soil of the roadbed should be taken into account. The condition of road structures, the level of compliance of their parameters with the operational requirements, as well as the quality and compliance of finished structures, determine the possibility of full use of road resources when creating adequate mathematical models that accurately and fully characterize the physical essence of their work [3].

2. Materials and methods

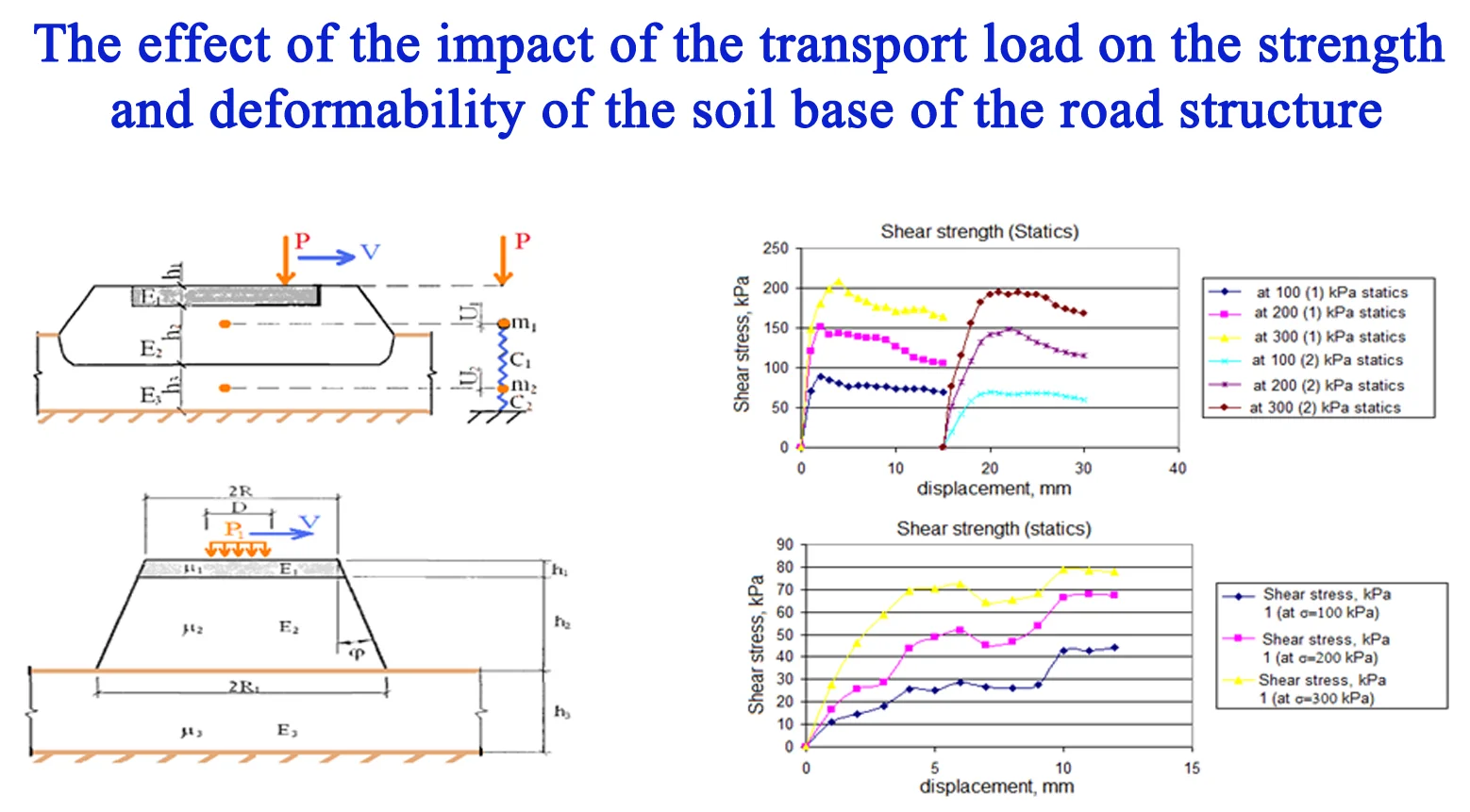
The calculation of deflections of road structures on ordinary homogeneous soils is carried out under the assumption that the physical model of the soil foundation is represented as a continuous elastic half-space [4]. To determine the deflections of complex layered structures under the action of a moving load, they are replaced by oscillatory systems with one degree of freedom with concentrated masses, to which solutions of the theory of vibrations are applicable (see Fig. 1) [2]. A concentrated force $P$ acts on the surface of the garment, changing sinusoidally over time and acting over a period of time $T_0=D/V$ (where $D$ is the calculated diameter of the track of a moving car wheel; $V$ is the speed of horizontal movement of the load).

Fig. 1Model of a road structure on a weak foundation: h1, h2, h3 is the thickness of the covering slab (subgrade and weak thickness, respectively); E1, E2, E3 is the modulus of elasticity of the slab (subgrade soil and weak subgrade)

In the oscillatory system, instead of physical masses, masses of pavement and layers of weak soil are introduced, brought to a point by the method of L. Damme [2]. This reduction takes into account the distributional ability of coatings and weak layers of the soil base. The differential equations of oscillations under the action of a short-term concentrated force for a two-mass system are written as:

where $m_1$ is the mass of the upper part of the road structure reduced to a point (road clothing and soil of the upper part of the roadbed); $m_2$ is the mass of the lower part of the road structure reduced to a point (soil of the lower part of the roadbed and a weak soil base); $c_1$, $c_2$ is the are the stiffness coefficients of the upper and lower parts of the road structure $c_2\frac{27E_2}{h_1}$; $U_1$, $U_2$ is the dynamic deflections of the upper and lower parts of the road structure $\left(U=U_1+U_2\right)$; $t$ is the time.

For the above calculation scheme, we have a differential equation of oscillations under the action of a short-term concentrated force for a two-mass system in the form [4].

In this case, the acceleration of fluctuations in the mass of weak soil ($m_2-a$) is obtained from the finite difference method in the form:

Having solved Eq. (1) and Eq. (2), we obtain expression Eq. (4) for calculating the acceleration of mass fluctuations $m_2$:

The calculation of the value a is performed under the condition $U_2=$1 mm (maximum deformation of precast cement concrete coatings), $t=D/V=$ 34 cm/1660 cm/sec = 0,02 sec [4].

The values of the incoming quantities are determined by the expressions:

where $K_0=\frac{E_2\left(1-v_3\right)}{h_3\left(1+v_3\right)\left(1+2v_3\right)}$ is the coefficient of the soil bed of the lower part of the roadbed, MPa; $K_0^{\text{'}}=\frac{E_2^{\text{'}\text{'}}\left(1-v_3\right)}{h_2\left(1+v_2\right)\left(1+2v_2\right)}$ is the coefficient of the soil bed of the upper part of the roadbed, MPa; $K$ is the radius of the deflection bowl, m; $E\text{'}\text{'}$ is the equivalent modulus of elasticity of an embankment consisting of soil and loam, MPa; $E_1$, $E_2$, $E_3$ is the elastic modulus, respectively, of the pavement, the soil of the earth bed and the weak soil base, MPa; $h_1$, $h_2$, $h_3$ is the thicknesses of the layers, respectively, of the pavement, the earth bed and the weak soil base, m; $v_1$, $v_2$, $v_3$ is the Poisson coefficients of the corresponding layers [4].

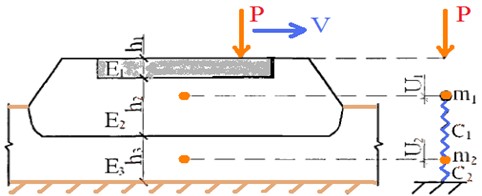
If we compare the values of the accelerations of vibrations of a weak ground base, determined by this calculated oscillatory system, at $h_1=$ 0.14 m, $E_1=$ 35,000 MPa; $h_2=$ 2.0 m, $E_2=$ 80 MPa; $h_3=$ 1.0 m, $E_3=$ 3 MPa, amounting to 108.48 mm/s², with experimental values of accelerations fluctuations of weak soil amounting to 140.48 mm/s², then the deviation between them will be 30 %. The combination of the upper and lower monolithic layers can be arbitrary, unlike the current methods of calculating road clothes. In the model (see Fig. 2), the coating is represented by a plate that has the following characteristics: thickness $h_1$, modulus of elasticity $E_1$ and Poisson’s ratio ${\mu }_1$, material density $p_1$. A roadbed with a thickness of – $h_2$ with an elastic modulus of $E_2$ and a material density of $p_2$ is based on a weak soil thickness of $h_3$ with an elastic modulus of $E_3$, a Poisson’s ratio of $m_3$ and a density of $p_3$. From the calculation scheme, it is possible to determine the size of the deflection bowl in plan $\mathfrak{R}$.

Using the modulus of elasticity or the bed coefficient as the elastic characteristic of the base is sufficient to solve the problem of deformations. With a limited capacity of the compressible layer – the “active zone”, there is a functional relationship between the bed coefficient $K_3$ and the elastic modulus $E_3$ [5]:

Fig. 2Design diagram of a layered road structure on a weak soil base

The dynamic load acting on the road clothes moves along the surface [6]. When exposed to it, the inertial properties of the “road clothes - roadbed - weak soil foundation” system are manifested, which are taken into account by introducing into the calculation the size of the array of the road structure involved in the oscillatory process, as well as its density [7]. The mass of the road structure involved in vibrations can be found from the condition that these vibrations occur due to deformation of a weak thickness [8]. The dimensions of the zone (the dimensions of the deflection bowl) are determined by the dimensions of the deformable surface of the coating under the influence of the wheel of the calculated car [9]. The upper layer of the structure is a plate with cylindrical rigidity $D_1$:

The radius of rigidity of a plate lying on an elastic base is determined by the dependence. The radius of the deformation zone $\mathfrak{R}$ in the plan is equal to:

The mass of this body will be:

where $h$ is the total thickness of the layers of the base of the pavement and the roadbed, m; $p$ is the weighted average density of the materials of the layers, t/m³.

The frequency of the coating load is determined by the expression [10]:

where $C_s$ is the stiffness of a weak soil base ($C_s=C\pi R^2$).

3. Results and discussion

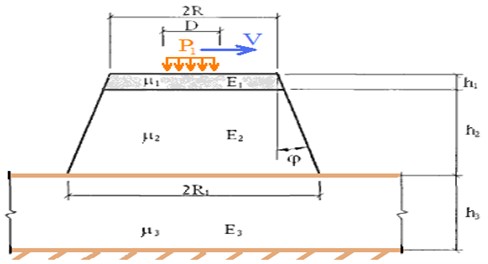
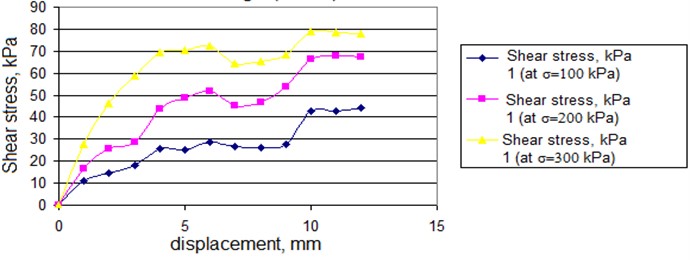
Graphs of soil shear resistance under static influence in the coordinates “tangential stress – displacement” are shown in Figs. 3-5. The tendency to increase shear resistance to a certain stabilized limit value is clearly visible [11]. Tests in static mode showed the absence of peak resistance and the following parameters are set for loam in the limiting state ${\phi }_{st}=$37.1 rad, $C_s=$20.5 kPa.

Fig. 3Diagrams of shear resistance under dynamic loading

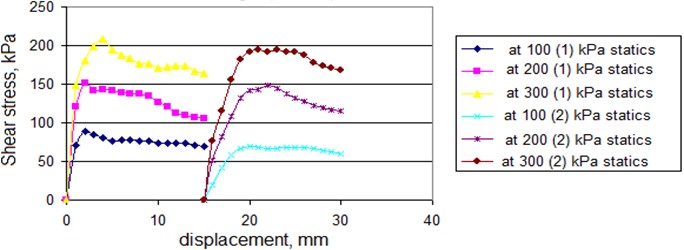
Fig. 4Diagrams of the limiting state of loam under static and dynamic loading, taking into account changes in stress in the shear plane

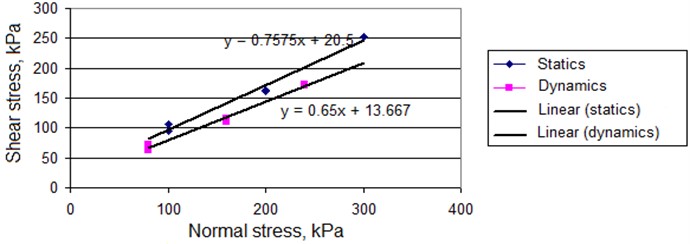
Fig. 5Diagrams of shear resistance of alternating loading of soil with static and dynamic loads

4. Conclusions

The proposed method makes it possible to determine the values of the accelerations of vibrations of the “road clothes - roadbed - weak soil base” system at the “roadbed - weak soil base” boundary under repeated dynamic loading. As a result of calculating the accelerations of vibrations of weak soil, with a plate thickness of 0.14 m ($E=$ 35,000 MPa), a change in the height of the sand embankment from 1.5 to 2.5 m ($E_2=$ 60, 80, 100 MPa) and with a layer thickness of weak soil from 1.0 to 4.0 m ($E_3=$ 3, 7, 15 MPa) – the acceleration of vibrations at the “roadbed – weak soil” boundary varies from 59.3 to 128.6 mm/s², that is, in the range from 0.005 to 0.01 g. The discrepancy between the calculated and experimental data does not exceed 13 %. Based on the conducted experimental and theoretical studies, a methodology has been developed to test the stability of road structures on a weak soil base under dynamic influences.