Tensor analysis of tornadoes: a new analytical and numerical model

1. Introduction

The Indonesian government is currently focusing on phenomena such as heat waves that have received attention, as well as tornadoes that have devastated various regions of Indonesia. A tornado hit Lebak Banten, Indonesia, on May 10, 2022. This incident caused damage to about 80 houses and schools. Tornadoes wreaked devastation in several districts of Lebak, Banten, resulting in losses of thousands of millions of rupiah. A tornado had also ripped across the Subang area the day before. The Regional Disaster Management Agency (BPBD) of Subang Regency claimed 21 locations were affected by the hurricane, with Cibogo and Subang Kota Districts suffering the most damage [1]. Tornado parameters must be studied due to their catastrophic impact. In recent years, physicists have employed computational physics and fluid mechanics to examine and model different natural processes, as well as material science [2-8]. Tornado investigation is an intriguing topic in Earth’s atmosphere and geophysical sciences. Tornadoes are hazardous natural disasters that strike on a small scale and last only a few minutes. Actual tornado observations are difficult to collect [9]. Despite improvements in severe storm mathematical approaches, replicating and predicting small-scale tornadoes will remain difficult [2]. As a result, a computerized model has arisen as a way of studying and modeling tornadoes. Several researchers have been performed to simulate the tornado mechanism [2-4]. Scientists first used computational modeling to simulate tornadoes [10, 11]. Computation physics modeling, including artificial intelligence and numerical modeling, has various advantages over other forms of research approaches, including lower risk [5-7], lower cost [12, 13], and the need for fewer experimental data [14-18]. Computational dynamics enables researchers to further accurately compute various tornado patterns, wind direction and speed, latitude, the impacts of Earth's rotation as well as Coriolis forces, and wind pressure to completely comprehend and model tornado formation. Tornadoes & wind patterns are examples of the Coriolis effect. A tornado is distinguished by a low-pressure region with rising pressure at its center. Tornadoes, which divert airflow from all directions, need the Coriolis force to circulate. As a result, hurricanes hardly form in tropical areas and never cross the Equator [19-21]. This study gives a simple 2D and 3D model for generating a tornado-like vortex utilizing an advanced model and computation using tensor analysis reported by various researchers [20, 22]. The scientific application of this finding is that researchers at the Meteorology, Climatology, and Geophysics Agency will be able to analyze a tornado and geophysical phenomena more readily with simulations and models [5, 23].

2. Research methods

2.1. Tornado mathematical model

The foundation of our work is the theoretical framework of variables used to describe motion. Eq. (1) expresses the acceleration in a fixed system in terms of location, speed, and acceleration in the rotating system:

1

$a={\ddot{r}}^{\text{'}}+\dot{\omega }\times r^{\text{'}}+2\omega \times {\dot{r}}^{\text{'}}+\omega \times \omega \times r^{\text{'}},$

where $\omega$ is the angular velocity, $\dot{\omega }$ is the time derivative of $\omega$ and $r\text{'}$, ${\dot{r}}^{\text{'}}$ and ${\ddot{r}}^{\text{'}}$ are the position in the unit (m), velocity in the unit (m/s), and acceleration in the unit (m/s²), respectively. In the case where the primed system undergoes both translation and rotation, we obtain general equations for transforming from a fixed to a moving and rotating system, as shown in Eq. (2). This comprises the generic equations for transforming a stationary system into a moving and rotating one:

2

$a={\ddot{r}}^{\text{'}}+\dot{\omega }\times r^{\text{'}}+2\omega \times {\dot{r}}^{\text{'}}+\omega \times \omega \times r^{\text{'}}+A.$

After we have the motion equation in moving coordinates, we can write it as shown in Eqs. (3) to (6):

3

$F=ma=m\left({\ddot{r}}^{\text{'}}+\dot{\omega }\times r^{\text{'}}+2\omega \times {\dot{r}}^{\text{'}}+\omega \times \omega \times r^{\text{'}}+A\right),$

4

$F-m\left(\dot{\omega }\times r^{\text{'}}+2\omega \times {\dot{r}}^{\text{'}}+\omega \times \omega \times r^{\text{'}}+A\right)=m{\ddot{r}}^{\text{'}},$

5

$F-\left(m\dot{\omega }\times r^{\text{'}}+2m\omega \times {\dot{r}}^{\text{'}}+m\omega \times \left(\omega \times r^{\text{'}}\right)+mA\right)=m{\ddot{r}}^{\text{'}},$

6

$F-\left(F_{Eul}+F_{cor}+F_{cent}+F_t\right)=m{\ddot{r}}^{\text{'}},$

where $F$ is the physical force, $F_{eul}=m\dot{\omega }\times r^{\text{'}}$ is the Euler force, $\omega$ is the angular velocity, $F_{cor}=2m\omega \times {\dot{r}}^{\text{'}}$ is the Coriolis force, $F_{cent}=m\omega \times \left(\omega \times r^{\text{'}}\right)$ denotes the centrifugal force, and $F_t=mA$ denotes the force due to the translation of the coordinate system. The equation of motion in a moving system can be written as Eq. (7):

7

$\sum F_{all}=m{\ddot{r}}^{\text{'}}=\rho V{\ddot{r}}^{\text{'}},\sum f=\rho {\ddot{r}}^{\text{'}},$

where $f$ is the total force per unit volume, $\rho$ is the density of the particle with a certain mass, and ${\ddot{r}}^{\text{'}}$ is the acceleration of the particle with a certain mass. We can extend the model by using Cauchy's equation in Eq. (8) and the generalized equation of motion in 3D movement proposed by [22] as in Eqs. (9) and (10):

8

$\nabla \bullet \sigma +f_{tot}=\rho {\ddot{r}}^{\text{'}},$

9

$\nabla \bullet \sigma +f_g-\left(f_{Eul}+f_{cor}+f_{cent}+f_t\right)=\rho \left({\ddot{x}}^{\text{'}}+{\ddot{y}}^{\text{'}}+{\ddot{z}}^{\text{'}}\right),$

10

$\nabla \bullet \sigma +f_g-f_{Eul}-f_{cor}-f_{cent}-f_t=\rho \left({\ddot{x}}^{\text{'}}+{\ddot{y}}^{\text{'}}+{\ddot{z}}^{\text{'}}\right),$

where $f_{tot}$ is the total force per unit volume, $f_g$ is the gravitational attraction force, $\rho$ is the density of the particle with a certain mass, and $\sigma$ is the stress tensor. Consider the Euler force $f_{Eul}=0$, the force due to the translation of the coordinate system $f_t=0$, and since the centrifugal force is so small compared to the other terms, we can neglect it. The equation of motion then becomes:

11

$\left(\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\sigma }_{yx}}{\partial y}+\frac{\partial {\sigma }_{zx}}{\partial z}\right){\mathbf{i}}^{\mathbf{\text{'}}}+\left(\frac{\partial {\sigma }_{xy}}{\partial x}+\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\sigma }_{zy}}{\partial z}\right){\mathbf{j}}^{\mathbf{\text{'}}}+\left(\frac{\partial {\sigma }_{xz}}{\partial x}+\frac{\partial {\sigma }_{yz}}{\partial y}+\frac{\partial {\sigma }_{zz}}{\partial z}\right){\mathbf{k}}^{\mathbf{\text{'}}}-\rho g{\mathbf{k}}^{\mathbf{\text{'}}}-2\rho \left({\omega }_x{\mathbf{i}}^{\mathbf{\text{'}}}+{\omega }_y{\mathbf{j}}^{\mathbf{\text{'}}}+{\omega }_z{\mathbf{k}}^{\mathbf{\text{'}}}\right)\times \left({\dot{x}}^{\text{'}}{\mathbf{i}}^{\mathbf{\text{'}}}+{\dot{y}}^{\text{'}}{\mathbf{j}}^{\mathbf{\text{'}}}+{\dot{z}}^{\text{'}}{\mathbf{k}}^{\mathbf{\text{'}}}\right)=\rho \left({{\ddot{x}}^{\text{'}}+{\ddot{y}}^{\text{'}}+{\ddot{z}}^{\text{'}}}^{\mathbf{\text{'}}}\right),$

12

$f_{px}{\mathbf{i}}^{\mathbf{\text{'}}}+f_{py}{\mathbf{j}}^{\mathbf{\text{'}}}+f_{pz}{\mathbf{k}}^{\mathbf{\text{'}}}-\rho g{\mathbf{k}}^{\mathbf{\text{'}}}-2\rho \left({\omega }_x{\mathbf{i}}^{\mathbf{\text{'}}}+{\omega }_y{\mathbf{j}}^{\mathbf{\text{'}}}+{\omega }_z{\mathbf{k}}^{\mathbf{\text{'}}}\right)\times \left({\dot{x}}^{\text{'}}{\mathbf{i}}^{\mathbf{\text{'}}}+{\dot{y}}^{\text{'}}{\mathbf{j}}^{\mathbf{\text{'}}}+{\dot{z}}^{\text{'}}{\mathbf{k}}^{\mathbf{\text{'}}}\right)=\rho \left({{\ddot{x}}^{\text{'}}+{\ddot{y}}^{\text{'}}+{\ddot{z}}^{\text{'}}}^{\mathbf{\text{'}}}\right).$

To simplify the calculation of the model, it can be assumed that:

$\left(\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\sigma }_{yx}}{\partial y}+\frac{\partial {\sigma }_{zx}}{\partial z}\right){\mathbf{i}}^{\mathbf{\text{'}}}+\left(\frac{\partial {\sigma }_{xy}}{\partial x}+\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\sigma }_{zy}}{\partial z}\right){\mathbf{j}}^{\mathbf{\text{'}}}+\left(\frac{\partial {\sigma }_{xz}}{\partial x}+\frac{\partial {\sigma }_{yz}}{\partial y}+\frac{\partial {\sigma }_{zz}}{\partial z}\right){\mathbf{k}}^{\mathbf{\text{'}}}=f_{px}{\mathbf{i}}^{\mathbf{\text{'}}}+f_{py}{\mathbf{j}}^{\mathbf{\text{'}}}+f_{pz}{\mathbf{k}}^{\mathbf{\text{'}}},$

${\omega }_x{\mathbf{i}}^{\mathbf{\text{'}}}+{\omega }_y{\mathbf{j}}^{\mathbf{\text{'}}}+{\omega }_z{\mathbf{k}}^{\mathbf{\text{'}}}=\left(0{\mathbf{i}}^{\mathbf{\text{'}}}+\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda {\mathbf{j}}^{\mathbf{\text{'}}}+\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda {\mathbf{k}}^{\mathbf{\text{'}}}\right),$

yield:

13

$f_{px}{\mathbf{i}}^{\mathbf{\text{'}}}+f_{py}{\mathbf{j}}^{\mathbf{\text{'}}}+f_{pz}{\mathbf{k}}^{\mathbf{\text{'}}}-\rho g{\mathbf{k}}^{\mathbf{\text{'}}}=\rho \left({\ddot{\mathbf{r}}}^{\mathbf{\text{'}}}\right)+2\rho \left({\omega }_x{\mathbf{i}}^{\mathbf{\text{'}}}+{\omega }_y{\mathbf{j}}^{\mathbf{\text{'}}}+{\omega }_z{\mathbf{k}}^{\mathbf{\text{'}}}\right)\times ({\dot{x}}^{\text{'}}\mathbf{i}+{\dot{y}}^{\text{'}}\mathbf{j}+{\dot{z}}^{\text{'}}\mathbf{k})$

14

$f_{px}{\mathbf{i}}^{\mathbf{\text{'}}}+f_{py}{\mathbf{j}}^{\mathbf{\text{'}}}+f_{pz}{\mathbf{k}}^{\mathbf{\text{'}}}-\rho g{\mathbf{k}}^{\mathbf{\text{'}}}=\rho \left({\ddot{\mathbf{r}}}^{\mathbf{\text{'}}}+2\left(0{\mathbf{i}}^{\mathbf{\text{'}}}+\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda {\mathbf{j}}^{\mathbf{\text{'}}}+\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda {\mathbf{k}}^{\mathbf{\text{'}}}\right)\times \left({\dot{x}}^{\text{'}}\mathbf{i}+{\dot{y}}^{\text{'}}\mathbf{j}+{\dot{z}}^{\text{'}}\mathbf{k}\right)\right).$

We can write $g=\mathcal{}\mathcal{g}-{\omega }^{2}R\mathrm{c}\mathrm{o}\mathrm{s}\lambda$ because of the effect of Earth’s rotation. Where $\mathcal{g}$ denotes the actual gravitation acceleration, and ${\omega }^{2}R\mathrm{c}\mathrm{o}\mathrm{s}\lambda$ denotes the centripetal acceleration for the Earth’s radius, $R$, and geocentric latitude, $\lambda$. In this study, we choose the coordinate axis $O\text{'}x\text{'}y\text{'}z\text{'}$ such that the $z\text{'}$ is vertical, the $x\text{'}$ axis to the east, and the $y\text{'}$ axis points north. The coordinate axes for analyzing tornado motion can be shown in Fig. 1.

Fig. 1Coordinate axes for analyzing tornado motion.

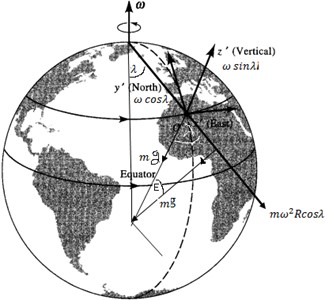
We also use ${\omega }_x=0$, ${\omega }_y=\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda \text{,}$ and ${\omega }_z=\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda .$ Eq. (14) can be solved computationally, and we get Eqs. (15) and (16):

15

$f_{px}{\mathbf{i}}^{\mathbf{\text{'}}}+f_{py}{\mathbf{j}}^{\mathbf{\text{'}}}+f_{pz}{\mathbf{k}}^{\mathbf{\text{'}}}-\rho g{\mathbf{k}}^{\mathbf{\text{'}}}=\rho {\ddot{\mathbf{r}}}^{\mathbf{\text{'}}}+2\rho \left({\dot{z}}^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda -{\dot{y}}^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda \right){\mathbf{i}}^{\mathbf{\text{'}}}+2\rho \left({\dot{x}}^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda \right){\mathbf{j}}^{\mathbf{\text{'}}}-2\rho \left({\dot{x}}^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda \right){\mathbf{k}}^{\mathbf{\text{'}}},$

16

$\left(\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\sigma }_{yx}}{\partial y}+\frac{\partial {\sigma }_{zx}}{\partial z}\right){\mathbf{i}}^{\mathbf{\text{'}}}+\left(\frac{\partial {\sigma }_{xy}}{\partial x}+\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\sigma }_{zy}}{\partial z}\right){\mathbf{j}}^{\mathbf{\text{'}}}+\left(\frac{\partial {\sigma }_{xz}}{\partial x}+\frac{\partial {\sigma }_{yz}}{\partial y}+\frac{\partial {\sigma }_{zz}}{\partial z}\right){\mathbf{k}}^{\mathbf{\text{'}}}-\rho g{\mathbf{k}}^{\mathbf{\text{'}}}=\rho {\ddot{\mathbf{r}}}^{\mathbf{\text{'}}}+2\rho \left({\dot{z}}^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda -{\dot{y}}^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda \right){\mathbf{i}}^{\mathbf{\text{'}}}+2\rho \left({\dot{x}}^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda \right){\mathbf{j}}^{\mathbf{\text{'}}}-2\rho \left({\dot{x}}^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda \right){\mathbf{k}}^{\mathbf{\text{'}}}.$

We can solve Eq. (16); hence we find Eqs. (17) to (19):

17

${\ddot{\mathbf{x}}}^{\mathbf{\text{'}}}=\frac{1}{\rho }\left(\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\sigma }_{yx}}{\partial y}+\frac{\partial {\sigma }_{zx}}{\partial z}\right)-2\omega \left({\dot{z}}^{\text{'}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -{\dot{y}}^{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right),$

18

${\ddot{\mathbf{y}}}^{\mathbf{\text{'}}}=\frac{1}{\rho }\left(\frac{\partial {\sigma }_{xy}}{\partial x}+\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\sigma }_{zy}}{\partial z}\right)-2{\dot{x}}^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda ,$

19

${\ddot{\mathbf{z}}}^{\mathbf{\text{'}}}=\left(\frac{1}{\rho }\left(\frac{\partial {\sigma }_{xz}}{\partial x}+\frac{\partial {\sigma }_{yz}}{\partial y}+\frac{\partial {\sigma }_{zz}}{\partial z}\right)-g\right)+2{\dot{x}}^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda .$

Assuming that $\frac{\partial {\sigma }_{zz}}{\partial z}=\frac{R\rho T}{T}\frac{\partial \left(T\right)}{\partial z}+\frac{R\rho T}{\rho }\frac{\partial \left(\rho \right)}{\partial z}={\sigma }_o$, and ${\sigma }_{xx}={\sigma }_{xy}={\sigma }_{xz}={\sigma }_{yy}={\sigma }_{yz}=0$, hence we get $e_{zz}=\frac{{\sigma }_{zz}}{E}$, $e_{yy}=-v\frac{{\sigma }_{zz}}{E}$, and $e_{xx}=-v\frac{{\sigma }_{zz}}{E}$, $e_{xy}=e_{xz}=e_{yz}=0$, and we find Eqs. (20) to (22):

20

${\ddot{\mathbf{x}}}^{\mathbf{\text{'}}}=\frac{1}{\rho }\left(\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\sigma }_{yx}}{\partial y}+\frac{\partial {\sigma }_{zx}}{\partial z}\right)-2\omega \left({\dot{z}}^{\text{'}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -{\dot{y}}^{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)=-2\omega \left({\dot{z}}^{\text{'}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -{\dot{y}}^{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right),$

21

${\ddot{\mathbf{y}}}^{\mathbf{\text{'}}}=\frac{1}{\rho }\left(\frac{\partial {\sigma }_{xy}}{\partial x}+\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\sigma }_{zy}}{\partial z}\right)-2{\dot{x}}^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda =-2{\dot{x}}^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda ,$

22

${\ddot{\mathbf{z}}}^{\mathbf{\text{'}}}=\left(\frac{1}{\rho }\left(\frac{\partial {\sigma }_{xz}}{\partial x}+\frac{\partial {\sigma }_{yz}}{\partial y}+\frac{\partial {\sigma }_{zz}}{\partial z}\right)-g\right)+2{\dot{x}}^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda =\frac{{\sigma }_o}{\rho }-g+2{\dot{x}}^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda .$

We can integrate once concerning $t$ to get the component of velocity, and we find, as shown in Eqs. (23) to (25):

23

${\dot{\mathbf{x}}}^{\mathbf{\text{'}}}={\dot{x_o}}^{\mathbf{\text{'}}}-2\omega \left(z^{\text{'}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -y^{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right),$

24

${\dot{\mathbf{y}}}^{\text{'}}={\dot{y_o}}^{\mathbf{\text{'}}}-2x^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda ,$

25

${\dot{\mathbf{z}}}^{\mathbf{\text{'}}}={\dot{z_o}}^{\mathbf{\text{'}}}+\left(\frac{{\sigma }_o}{\rho }-g\right)t+2x^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda .$

Then substitute ${\dot{\mathbf{z}}}^{\mathbf{\text{'}}}$ and $\dot{\mathbf{y}}\text{'}$ into Eq. (20), we find Eqs. (26) and (27):

26

${\ddot{\mathbf{x}}}^{\mathbf{\text{'}}}=-2\omega \left({\dot{z}}^{\text{'}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -{\dot{y}}^{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)=-2\omega \left(\left[{\dot{z_o}}^{\mathbf{\text{'}}}+\left(\frac{{\sigma }_o}{\rho }-g\right)t+2x^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda \right]\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\left[{\dot{y_o}}^{\mathbf{\text{'}}}-2x^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda \right]\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right),$

27

${\ddot{\mathbf{x}}}^{\mathbf{\text{'}}}=-2\omega \left(\left[{\dot{z_o}}^{\mathbf{\text{'}}}+\left(\frac{{\sigma }_o}{\rho }-g\right)+2x^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda \right]\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\left[{\dot{y_o}}^{\mathbf{\text{'}}}-2x^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda \right]\mathrm{}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)\cong -2\omega {\dot{z_o}}^{\mathbf{\text{'}}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -2\mathrm{\omega }\left(\frac{{\sigma }_o}{\rho }-g\right)t\mathrm{c}\mathrm{o}\mathrm{s}\lambda +2\omega {\dot{y_o}}^{\mathbf{\text{'}}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda =2\omega \left(g-\frac{{\sigma }_o}{\rho }\right)t\mathrm{c}\mathrm{o}\mathrm{s}\lambda -2\mathrm{\omega }\left({\dot{z_o}}^{\mathbf{\text{'}}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\dot{y_o}\mathbf{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right).$

We integrate Eq. (27) again to get $\dot{x}\mathbf{\text{'}}$, as shown in Eq. (28) and Eq. (29):

28

$\int d\dot{x}\text{'}=\int \left[2\omega \left(g-\frac{{\sigma }_o}{\rho }\right)t\mathrm{c}\mathrm{o}\mathrm{s}\lambda -2\omega \left({\dot{z_o}}^{\mathbf{\text{'}}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\dot{y_o}\mathbf{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)\right]dt,$

29

${\dot{x}}^{\mathbf{\text{'}}}=\omega \left(g-\frac{{\sigma }_o}{\rho }\right)t^2\mathrm{c}\mathrm{o}\mathrm{s}\lambda -2\omega t\left({\dot{z_o}}^{\mathbf{\text{'}}}cos\lambda -\dot{y_o}\mathbf{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)+{\dot{x_o}}^{\text{'}},$

and finally, we find $x^{\text{'}}$ by integrating Eq. (29):

30

$x^{\text{'}}=\frac{\omega \left(g-\frac{{\sigma }_o}{\rho }\right)t^3}{3}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\mathrm{\omega }{t}^2\left({\dot{z_o}}^{\mathbf{\text{'}}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\dot{y_o}\mathbf{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)+{\dot{x_o}}^{\text{'}}t+x_o^{\text{'}}.$

Then substitute Eq.(30) into Eqs. (24) and (25), we find Eqs. (31) and (32):

31

${\dot{\mathbf{y}}}^{\text{'}}={\dot{y_o}}^{\mathbf{\text{'}}}-2x^{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda ={\dot{y_o}}^{\mathbf{\text{'}}}-2\left(\frac{\omega g{t}^3}{3}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\omega t^2\left({\dot{z_o}}^{\mathbf{\text{'}}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\dot{y_o}\mathbf{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)+{\dot{x_o}}^{\text{'}}t+x_o\text{'}\right)\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda \cong {\dot{y_o}}^{\mathbf{\text{'}}}-2\left({\dot{x_o}}^{\text{'}}t\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda +x_o\mathrm{\text{'}}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)$

32

${\dot{z}}^{\text{'}}={\dot{z_o}}^{\text{'}}+\left(\frac{{\sigma }_o}{\rho }-g\right)t+2x^{\text{'}}\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda ={\dot{z_o}}^{\mathrm{\text{'}}}+\left(\frac{{\sigma }_o}{\rho }-g\right)t$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+2\left(\frac{\omega \left(g-\frac{{\sigma }_o}{\rho }\right)t^3}{3}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\mathrm{\omega }{t}^2\left({\dot{z_o}}^{\mathrm{\text{'}}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\dot{y_o}\mathrm{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)+{\dot{x_o}}^{\text{'}}t\right)\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda .$

As a result of integrating Eqs. (31) and (32), the positions, $y^{\text{'}}$ and $z^{\text{'}}$, are given by:

33

$y^{\text{'}}={\dot{y_o}}^{\mathbf{\text{'}}}t-2\left(\frac{{\dot{x_o}}^{\text{'}}{t}^2}{2}\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda +x_o\mathrm{\text{'}}t\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)+y_o^{\text{'}}=y_o^{\text{'}}+{\dot{y_o}}^{\mathbf{\text{'}}}t-{\dot{x_o}}^{\text{'}}{t}^2\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda -2x_o^{\text{'}}t\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda \approx y_o^{\text{'}}+{\dot{y_o}}^{\mathbf{\text{'}}}t-2x_o^{\text{'}}t\omega \mathrm{s}\mathrm{i}\mathrm{n}\lambda ,$

34

$z^{\text{'}}={\dot{z_o}}^{\mathbf{\text{'}}}t+z_o+\omega \mathrm{c}\mathrm{o}\mathrm{s}\lambda {\dot{x_o}}^{\text{'}}{t}^2+\frac{1}{2}\left(\frac{{\sigma }_o}{\rho }-g\right)t^2={\dot{z_o}}^{\mathbf{\text{'}}}t+\left({\omega }^2{r}_o^{\text{'}}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\lambda }+\frac{1}{2}\left(\frac{{\sigma }_o}{\rho }-g\right)\right)t^2+z_o.$

According to some scientists [19, 20], a tornado is a dangerous natural event that occurs on an insignificant scale and persists for only a few minutes. Assuming that $y_o^{\text{'}}+{\dot{y_o}}^{\mathbf{\text{'}}}t=r_o^{\text{'}}$, $x_o^{\text{'}}=\dot{x_o}t=r_o^{\text{'}}\omega t$, and $\dot{x_o}=\dot{y_o}=\dot{z_o}=r_o^{\text{'}}\omega$, $\dot{r_o}$is so small at a very short time, we get Eqs. (35) and (36):

35

$x^{\text{'}}=\frac{\omega g{t}^3}{3}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\omega t^2\left({\dot{z_o}}^{\mathbf{\text{'}}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\dot{y_o}\mathbf{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)+{\dot{x_o}}^{\text{'}}t=\frac{\omega g{t}^3}{3}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\omega t^2\left({\dot{z_o}}^{\mathbf{\text{'}}}\mathrm{c}\mathrm{o}\mathrm{s}\lambda -\dot{y_o}\mathbf{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}\lambda \right)+r_o^{\text{'}}\omega t\approx r_o^{\text{'}}\omega t,$

36

$y^{\text{'}}=r_o^{\text{'}}-2r_o^{\text{'}}{\omega }^2{t}^2\mathrm{}\mathrm{s}\mathrm{i}\mathrm{n}\lambda =r_o^{\text{'}}\left(1-2\mathrm{s}\mathrm{i}\mathrm{n}\lambda {\omega }^2{t}^2\right)=r\left(1-\frac{{\left(\omega t\right)}^2}{2}\right)=r_o^{\text{'}}\cos \left(\omega t\right).$

Which requires that $2\mathrm{s}\mathrm{i}\mathrm{n}\lambda =\frac{1}{2}$ or $\mathrm{s}\mathrm{i}\mathrm{n}\lambda =\frac{1}{4}$ or $\lambda \approx$15° (that is near the Equator), we find:

37

$x^{\text{'}}=r_o^{\text{'}}\omega t=r_o^{\text{'}}\sin \left(\omega t\right),$

38

$y^{\text{'}}=r_o^{\text{'}}\cos \left(\omega t\right),$

39

$z^{\text{'}}={\dot{z_o}}^{\mathbf{\text{'}}}t+\left({\omega }^2+\frac{1}{2\mathrm{c}\mathrm{o}\mathrm{s}\lambda }\left(\frac{{\sigma }_o}{\rho }-g\right)\right)t^2\mathrm{}\mathrm{c}\mathrm{o}\mathrm{s}\lambda +z_o=r_o^{\text{'}}\omega t+\left({\omega }^2+\frac{1}{2\mathrm{c}\mathrm{o}\mathrm{s}\lambda }\left(\frac{{\sigma }_o}{\rho }-g\right)\right)t^2\mathrm{}\mathrm{c}\mathrm{o}\mathrm{s}\lambda .$

From Eqs. (37) to (39), we get Eqs. (40) to (42):

40

$x^{\text{'}}=r_o^{\text{'}}\sin \left(\omega t\right)=r_o^{\text{'}}\cos \left(90^o-\omega t\right),$

41

$y^{\text{'}}=r_o^{\text{'}}\cos \left(\omega t\right)=r_o^{\text{'}}\sin \left(90^o-\omega t\right),$

42

$z^{\text{'}}=r_o^{\text{'}}\omega t+\left({\omega }^2+\frac{1}{2\mathrm{c}\mathrm{o}\mathrm{s}\lambda }\left(\frac{{\sigma }_o}{\rho }-g\right)\right)t^2\mathrm{}\mathrm{c}\mathrm{o}\mathrm{s}\lambda .$

Assuming that $r_o^{\text{'}}={\dot{r_o}}^{\mathbf{\text{'}}}t$, and ignoring the effects of gravitational force and humidity, and using the equation of state, we obtain Eqs. (43) to (45):

43

$z^{\text{'}}=r_o^{\text{'}}\omega t+\left({\omega }^2+\frac{1}{2\mathrm{c}\mathrm{o}\mathrm{s}\lambda }\left(\frac{{\sigma }_o}{\rho }\right)\right)t^2\mathrm{}\mathrm{c}\mathrm{o}\mathrm{s}\lambda ,$

44

$z^{\text{'}}=r_o^{\text{'}}\omega t+\left({\omega }^2+\frac{1}{2\mathrm{c}\mathrm{o}\mathrm{s}\lambda }\left(\frac{1}{\rho }\frac{\partial {\sigma }_{zz}}{\partial z}\right)\right)t^2\mathrm{}\mathrm{c}\mathrm{o}\mathrm{s}\lambda ,$

45

$z^{\text{'}}={\dot{r_o}}^{\mathbf{\text{'}}}{t}^2+\left({\omega }^2+\frac{1}{2\rho \mathrm{c}\mathrm{o}\mathrm{s}\lambda }\left(\frac{\partial {\sigma }_{zz}}{\partial z}\right)\right)t^2\mathrm{}\mathrm{c}\mathrm{o}\mathrm{s}\lambda .$

According to [21], in the condition of a static atmosphere, we can write $\frac{\partial {\sigma }_{zz}}{\partial z}=\frac{\partial \left(R\rho T\right)}{\partial z}$. The density $\rho$ and pressure of the air ${\sigma }_{zz}$ in Eq (44) vary with height $z$. These changes can be calculated from the equation of state; we obtain:

46

$\frac{d\left({\sigma }_{zz}\right)}{dz}=R\rho \frac{\partial \left(T\right)}{\partial z}+RT\frac{\partial \left(\rho \right)}{\partial z},$

47

$\frac{d\left({\sigma }_{zz}\right)}{dz}=\frac{R\rho T}{T}\frac{\partial \left(T\right)}{\partial z}+R\rho T\frac{1}{\rho }\frac{\partial \left(\rho \right)}{\partial z},$

48

$\frac{1}{{\sigma }_{zz}}\frac{d\left({\sigma }_{zz}\right)}{dz}=\frac{1}{T}\frac{\partial \left(T\right)}{\partial z}+\frac{1}{\rho }\frac{\partial \left(\rho \right)}{\partial z},$

where $T$ is an absolute temperature, and $R$ is the specific gas constant of dry air. In Eq. (48), the density $\rho$ and $T$ vary with altitude, and assuming that $\frac{1}{{\sigma }_{zz}}\frac{d\left({\sigma }_{zz}\right)}{dz}=\frac{1}{2\rho }\left(\frac{\partial {\sigma }_{zz}}{\partial z}\right)$, then we obtain the position $z^{\text{'}}$, which indicates the height of tornadoes as shown in Eq. (49):

49

$z^{\text{'}}={\dot{z_o}}^{\mathbf{\text{'}}}t+\left({\omega }^2\mathrm{c}\mathrm{o}\mathrm{s}\lambda +\frac{1}{2\rho }\left(\frac{\partial {\sigma }_{zz}}{\partial z}\right)\right)t^2={r_o}^{\mathbf{\text{'}}}\omega t+\left({\omega }^2\mathrm{c}\mathrm{o}\mathrm{s}\lambda +\left(\frac{1}{T}\frac{\partial \left(T\right)}{\partial z}+\frac{1}{\rho }\frac{\partial \left(\rho \right)}{\partial z}\right)\right)t^2.$

where $2\rho ={\sigma }_{zz}$ is related to tornado pressure.

3. Results and discussions

Fig. 2 shows a two-dimensional model of a tornado with the velocity of the wind varying to the west and north throughout the same period. Modeling results show that the greater the wind velocity to the north and west, the larger the region of the tornado movement. The simulation findings reveal that the tornado’s area of rotation is affected by the velocity of the wind, tornado time, and earth rotational speed. The tornado may rotate and require Coriolis force to move.

Fig. 2Two-dimensional simulation of a tornado with wind speed variations

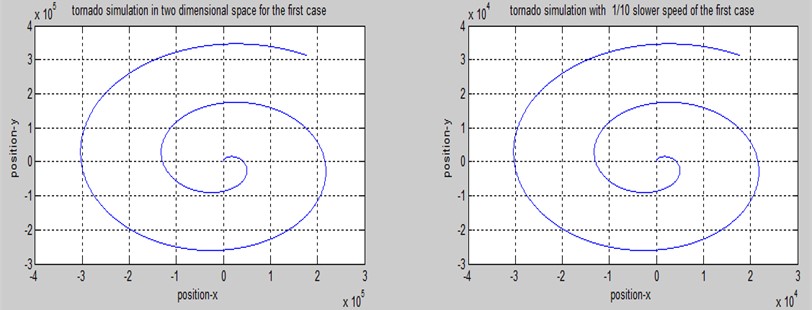
Fig. 3Three-dimensional simulation of a tornado with wind speed and geocentric latitude variations

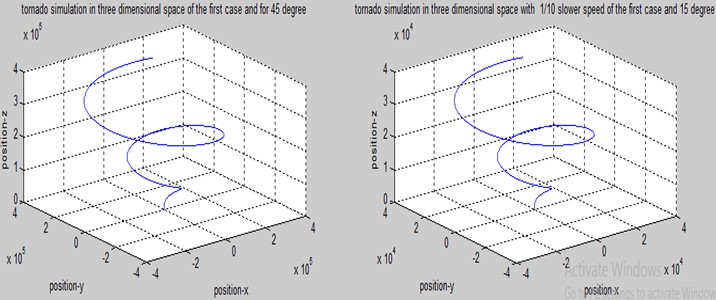
Fig. 3 shows a three-dimensional simulation of a tornado with variations in wind speed to the west and north over the same period and geocentric latitude variations of 45 degrees and 15 degrees. Fig. 4 shows a tornado at Mount Kencana, Banten, Indonesia, where a tornado appears when there is a change in temperature and high density, as well as a high wind rotation. Based on Fig. 3 and Fig. 4, we found a strong correlation between tornado height, air density and temperature, geocentric latitude, and initial speed, as shown in Eq. (49). As a result of our investigation and model results, we find that tornadoes have a low-pressure area with an increasing-pressure core. Research shows that this model can describe the spiraling upward motion of air within a tornado's path without including vertical convection. In addition to high airspeeds in the upper atmosphere, geocentric latitude, and the Coriolis effect, higher atmospheric pressure also contributes to tornadoes. According to some researchers [2, 4, 10, 11, 14], tornadoes in the Northern Hemisphere move clockwise, which is consistent with our model at 45 degrees and 15 degrees. However, in the Southern Hemisphere, tornadoes normally move in the opposite direction or counterclockwise. As a result of the rotation of the Earth, the Coriolis effect deflects wind directions. Thus, the direction of a tornado’s motion is determined by which hemisphere it occurs in.

Fig. 4Tornado in Gunung kencana, Banten, Indonesia [1]

The problem of mathematically expressing places in three-dimensional space when simulating tornado formation is addressed by Eqs (40), (41), and (49). Eqs. (29), (31), and (32) provide solutions to the difficulty of mathematically describing wind velocity in forming tornadoes. The modeling results demonstrate that the higher the geocentric latitude angle, the more likely a tornado will form. This research suggests that huge tornadoes can form in places with high geocentric latitudes. In this study, we discovered the equation for the motion of a tornado in three-dimensional coordinates, as shown in Eqs. (17) through (19).

Our findings revealed a strong relation involving tornado height and changes in air density and temperature, as well as geocentric latitude and beginning speed, as given in Eq. (49). Our investigation and model results validate various academics' claims that a low-pressure area with an increasing-pressure core characterizes tornadoes. Tornadoes require Coriolis force for movement. As a result, storms are uncommon in tropical regions and rarely cross the Equator, and this study confirms prior observations [14-18]. According to the research, this model could describe the spiraling upward motion of air in a tornado's path without incorporating vertical convection. This model revealed no differences with experts' opinions that certain variables can cause tornadoes. Tornadoes are created by various elements, including geocentric latitude, the Coriolis effect, higher airspeed in the upper atmosphere, and higher atmospheric pressure [14-18]. The airflow characteristics of a tornado can be calculated by calculating the 3-D and mathematical models of airflow motion and the Earth’s rotation in three-dimensional (3D) space. This research provides a basic 2D and 3D model to generate a tornado-like vortex using simple modeling and calculation. This research’s scientific applicability is that professionals and scientific experts can utilize the models to study tornadoes more easily. The results of 2-D modeling and simulation indicated that the greater the initial tornado angular speed, the larger the tornado area. Three-dimensional modeling and simulation also show that tornadoes are more powerful at higher geocentric latitude angles.

4. Conclusions

This research reported a theoretical formulation of tornadoes in a non-inertial mechanics framework, utilizing fluid mechanics and numerical simulation. This model depicted the spiraling upward motion of air in a tornado while ignoring vertical convection. Several conditions were required for a tornado to occur, including geocentric latitude, the Coriolis effect, increased airspeed in the upper atmosphere, and increased air pressure. We calculated the airflow characteristics of a tornado and solved the three-dimensional position of the tornado or hurricane in three-dimensional (3D) space, as well as the differential equations of airflow velocity and the Earth’s rotation. To demonstrate tornado patterns, motion dynamics modeling, and numerical computations were performed using computer software. The study concluded that this model could explain tornado patterns. Using the modeling and simulation data from this work, practitioners and scientists can gain a better understanding of hurricanes. To obtain more precise models, we proposed that additional studies be performed utilizing various methodologies, such as quantum neural networks / QNNs and artificial neural networks in future research.