Secure metric dimension of new classes of graphs

1. Introduction

Let $G=(V,E)$ be a connected, simple, finite graph. On which the ordering $(x_1,x_2,...,x_k)$ is imposed, let $\stackrel{-}{S}=\{x_1,x_2,...,x_k\}$. The metric description of $b$ with regard to $\stackrel{-}{S}$is defined as the ordered $k$-tuples $r\left(b\right|\stackrel{-}{S})=(d(x_1,b),d(x_2,b),...,d(x_k,b))$ for each $b\in V\left(G\right)$. If $r\left(x\right|\stackrel{-}{S})=r(b\left|\stackrel{-}{S}\right)$ implies $x=b$ for every $x,b\in V\left(G\right)$, then the set $\stackrel{-}{S}$ is referred to as a resolving set of $G$. A minimal resolving set, also known as a basis, is a resolving set of $G$ with minimum cardinality. The dimension of $G$, represented by $dim\left(G\right)$, is the cardinality of a minimum resolving set [1].

There is previous study in the literature on the location of sets in a connected graph [2, 3]. Nearly forty years ago, Slater introduced the idea of finding sets (resolving sets) and a reference set (metric dimension). Afterwards, the aforementioned theory [4] was independently discovered by Harary and Melter. They started referring to location numbers as metric dimensions. On resolving sets, resolving dominating sets, independent resolving sets, etc., many papers have been composed. In a graph, the concept of security is linked to many kinds of sets. A dominating set $D$ of $G$ is a secure set, for instance, if there is an $x\in D$ such that $(D-\{u\left\}\right)\cup \left\{v\right\}$ is a dominating set for any $v\in V-D$ [5, 6]. Farooq et al. [7] studied the metric dimension of the line graph of the Bakelite network and subdivided the Bakelite network. According to [8], a path graph is the only graph with a metric dimension of 1. For $n\ge 3$, the metric dimension of the cycle graph is 2. This idea is especially helpful for applications including chemistry and space routing. For instance, in space routing, the objective is to assign the smallest number of robots feasible to certain vertices so that they can visit each vertex exactly once. The problem can be resolved by applying the idea of metric dimension. The minimal landmarks needed for the hexagonal network $HX\left(n\right)$ and the honeycomb network $HC\left(n\right)$ are three and six, respectively, according to research by Abbas et al. [9]. The local metric dimension of a number of specific line graphs was examined by Yang et al. [10]. Jothi et al. [11] investigated the relation between the metric dimension of a bipartite graph and its projections. Additionally, they provided some realization results for the bounds on the metric dimension of a bipartite graph. The dominant metric dimension of the generalized Petersen graph was examined by Susilowati et al. [12]. Mazidah et al. [13] examined the resolving independent domination number of path graph, cycle graph, friendship graph, helm graph and fan graph. The maximum number of vertices in a bipartite graph with a particular diameter and metric dimension was computed by Dankelmann et al. [14]. Additional details can be discovered in the literature [15-19].

Our main aim in this paper is to compute the secure resolving set of some graphs, including the join of $(m,n)$ Kite graph, the 1-join of square of path $P_n^2$graph, coconut tree $CT(m,n)$ and extended jewel graph.

Definition 1.1 The basis of the graph is the resolving set with the least vertices [7].

Definition 1.2 [20]: A $(m,n)$ Kite graph is made up of a cycle of length $m$ with $n$ edges and a path connected to one of the cycle's vertices.

Definition 1.3 [21]: A Coconut tree $CT(m,n)$: for any positive integers $n$ and $m\ge 2$ is derived from the path $P_m$ by attaching $n$ additional pendant edges at an end vertex of $P_m$.

Illustration 1.3. Consider ${∆}_5$, for which $R=\{u_1,u_4\}$. Then, $R$ is resolving, and for any $u\in V-R$, there exists $v\in R$ such that$(R-\{v\left\}\right)\cup \left\{u\right\})$ is a resolving set of ${∆}_5$. It can be easily seen that $sdim\left({∆}_5\right)=2$.

Fig. 1An example on a Kite graph

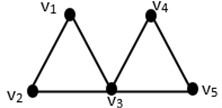
2. Secure resolving dimension for several known graphs [5, 6]

1. $sdim\left(K_n\right)=n-1=dim\left(K_n\right)$.

2. $sdim(K_1,n)=n>dim(K_1,n)$.

3. $sdim\left(K_{m,n}\right)=m+n-2=dim\left(K_{m,n}\right)$, $(m,n\ge 2)$.

4. $sdim\left(P_n\right)=2>dim\left(P_n\right)=1$, $(n\ge 3).$

5. $sdim\left(C_n\right)=2=dim\left(C_n\right)$.

6. For Trapezoid graph $T{r}_n$, $dim\left(T{r}_n\right)=2$ and $sdim\left(T{r}_n\right)=2$, for all $n\ge 6$.

7. For $Z-\left(P_n\right)$ graph, $dim(Z-(P_n\left)\right)=2$ and $sdim(Z-(P_n\left)\right)=2$.

8. For Tortoise graph $T{o}_n$, $dim\left(T{o}_n\right)=2$ and $sdim\left(T{o}_n\right)=2$.

9. $sdim(P_{2n}⊽P_n)=2=dim(P_{2n}⊽P_n)$.

3. Main results

Here, we demonstrate that the secure metric dimension of including the join of $(m,n)$ Kite graph, the 1-join of square of path $P_n^2$graph, coconut tree $CT(m,n)$ and extended jewel graph. We also derive the explicit formulas for the secure metric dimension of shadow graph of path $D_2\left(P_n\right)$, Jelly fish $J_{n,n}$, Lilly graph $L_n$, Twig graph ${Tg}_n$, Joint sum of two copies of $C_n$, quadrilateral graphs $Q_n$ and subdividing all the edges of $P_nʘK_1$.

Theorem 3.1: Let $G$ is Join of $(m,n)$ Kite graph $K_{m,n}$ with $n$ vertices and $\{v_1,v_{n/2+3}\}$ be a secure metric basis of $G$, then $sdim\left(K_{m,n}\right)=2$.

Fig. 2Join of (m, n) Kite graph Km,n

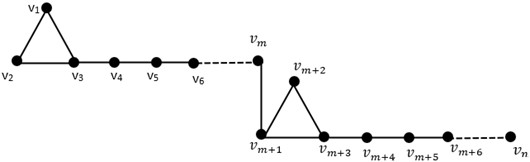
Proof. The secure resolving set in general form is $\stackrel{-}{S}=\{v_1,v_{m+3}\}\subset V\left(G\right)$. The following are representations of the vertices $v_i\in V\left(G\right)$ with respect to $\stackrel{-}{S}$:

Since all vertices have unique representations, we obtain $sdim\left(K_{m,n}\right)=2$.

Theorem 3.2: Let $G$ is 1-join of square of path $P_n^2$ with $n$ vertices and $\{v_1,v_{n/2+3}\}$ be a secure metric basis of $G$, then $sdim\left(P_n^2\right)=2$.

Fig. 31-join of square of path Pn2

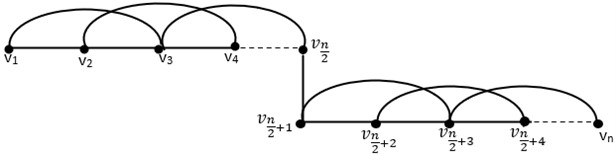
Proof. We label the 1-join of square of path $P_n^2$as shown in Fig. 2 such that $n$is the vertices number. It is clear that $\left|V\right(G\left)\right|$ is $n=k+4$. Let $\stackrel{-}{S}=\{v_2,v_{n-1}\}$.

Begin

$d(v_1$,$\stackrel{-}{S})=\left(1,\frac{n}{2}\right),$$d\left(v_2,\stackrel{-}{S}\right)=\left(0,\frac{n}{2}-1\right)$

for $(i=3;i<=\frac{n}{2};i=i+2)$

$d(v_i,\stackrel{-}{S})=\left(\frac{i-1}{2},\frac{n-i+1}{2}\right)$

end

for $(i=4;i<=\frac{n}{2}-1;i=i+2)$

$d(v_i,\stackrel{-}{S}$)=$\left(\frac{i}{2},\frac{n-i+2}{2}\right)$

end

for $(i=\frac{n}{2}+1;i<=n;i=i+2)$

$d\left(v_i,\stackrel{-}{S}\right)=\left(\frac{i}{2},\frac{n-i}{2}\right)$

end

for $(i=\frac{n}{2}+2;i<=n-1;i=i+2)$

$d\left(v_i,\stackrel{-}{S}\right)=\left(\frac{i+1}{2},\frac{n-i+1}{2}\right)$

end

end

This completes the proof.

Theorem 3.3: If $CT(m,n)$, $n\ge 2$, $m\ge 4$ is coconut tree, then $sdim\left(CT\right(m,n\left)\right)=m$.

Proof. The secure resolving set in general form is $\stackrel{-}{S}=\{v_1,v_2,v_{m-1},v_n\}\subset V\left(CT\right(m,n\left)\right)$. The representations of vertices $v_i\in V\left(CT\right(m,n\left)\right)$ in regard to $\stackrel{-}{S}$are as follow.

We choose a subset $\stackrel{-}{S}=\{v_1,v_2,v_3,\dots ,v_{m-1},v_n\}$, and we must demonstrate that $sdim\left(CT\right(m,n\left)\right)=m$ for $m\ge 4$ and $n\ge 3$. We obtained the representations of vertices in graph $CT(m,n)$ with respect to $\stackrel{-}{S}$are:

$r\left(v_1\right|\stackrel{-}{S})=(0,2,2,\dots ,2,m+2)$

$r\left(v_2\right|\stackrel{-}{S})=(2,0,2,\dots ,2,m+2)$

$r\left(v_3\right|\stackrel{-}{S})=(2,2,0,\dots ,2,m+2)$

$⋮$

$r\left(v_m\right|\stackrel{-}{S})=(2,2,2,\dots ,2,m+2)$

$r\left(v_{m+1}\right|\stackrel{-}{S})=(1,1,1,\dots ,1,m+1)$

$r\left(v_{m+2}\right|\stackrel{-}{S})=(i-m,i-m,\dots ,i-m,2m-i+2)$

$⋮$

$r\left(v_n\right|\stackrel{-}{S})=(i-m,i-m,\dots ,2m-i+2)$

Fig. 4Coconut tree CT(m, n)

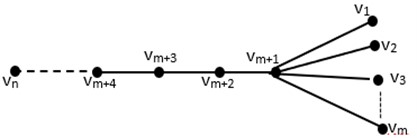
The representations of vertices in graph $CT(m,n)$ are distinct as seen above. This implies that $\stackrel{-}{S}$ is secure resolving set, but this does not prove that it is the lower bound. As a result, the upper bound is $sdim\left(CT\right(m,n\left)\right)\le m$. Now, we demonstrate that $sdim\left(CT\right(m,n\left)\right)\ge m$. Let $\stackrel{-}{S}=\{v_1,v_2,v_3,\dots ,v_{m-1},v_n\}$ be a secure resolving set with $\left|\stackrel{-}{S}\right|=m$. Assume that $\stackrel{-}{S_1}$ is another minimal resolving set, or $\left|\stackrel{-}{S_1}\right|<m$.

If we select an ordered set $\stackrel{-}{S_1}\subseteq \stackrel{-}{S}-\{v_i,v_j\}$, $1\le i,j\le m$, $i\ne j$, so that there exist two vertices $v_i,v_j\in CT(m,n)$such that $r\left(v_i\right|\stackrel{-}{S})=r(v_j\left|\stackrel{-}{S}\right)=(i-m,i-m,...,i-m)$. $\stackrel{-}{S_1}$is not a secure resolving set, which is contrary to assumption. As a result, $sdim\left(CT\right(m,n\left)\right)\ge m$ is the lower bound. From the above proving, we conclude that $sdim\left(CT\right(m,n\left)\right)=m$.

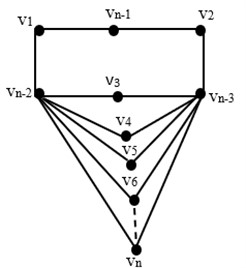
Theorem 3.4: If $E\left(j_n\right)$, $n\ge 7$, is extended jewel graph, then $sdim\left(E\right(j_n\left)\right)=n-4$.

Proof. We choose a subset $\stackrel{-}{S}=\{v_1,v_2,v_3,\dots ,v_{n-5},v_n\}$, and we must demonstrate that $sdim\left(E\right(j_n\left)\right)=n-4$ for $n\ge 7$. We obtained the representations of vertices in graph $E\left(j_n\right)$ with respect to $\stackrel{-}{S}$are:

$r\left(v_1\right|\stackrel{-}{S})=(0,2,2,\dots ,2,2)$

$r\left(v_2\right|\stackrel{-}{S})=(2,0,2,\dots ,2,2)$

$r\left(v_3\right|\stackrel{-}{S})=(2,2,0,\dots ,2,2)$

$⋮$

$r(v_n-5|\stackrel{-}{S})=(2,2,2,\dots ,2,\mathrm{0,2})$

$r(v_n-4|\stackrel{-}{S})=(2,2,2,\dots ,\mathrm{2,2})$

$r(v_n-3|\stackrel{-}{S})=(\mathrm{3,1},\dots ,1,1)$

$r(v_n-2|\stackrel{-}{S})=(\mathrm{1,3},1,\dots ,1,1)$

$r(v_n-1|\stackrel{-}{S})=(\mathrm{1,1},3,3,\dots ,3,3)$

$r\left(v_n\right|\stackrel{-}{S})=(2,2,\dots ,\mathrm{2,0})$

The representations of vertices in graph $E\left(j_n\right)$ are distinct as seen above. This implies that $\stackrel{-}{S}$is secure resolving set, but this does not prove that it is the lower bound. As a result, the upper bound is $sdim\left(E\right(j_n\left)\right)\le n-4$. Now, we demonstrate that $sdim\left(E\right(j_n\left)\right)\ge n-4$. Let $\stackrel{-}{S}=\{v_1,v_2,v_3,\dots ,v_{n-5},v_n\}$ be a secure resolving set with $\left|\stackrel{-}{S}\right|=n-4$. Assume that $\stackrel{-}{S_1}$ is another minimal resolving set, or $\left|\stackrel{-}{S_1}\right|<n-4$.

If we select an ordered set $\stackrel{-}{S_1}\subseteq \stackrel{-}{S}-\{v_i,v_j\}$, $1\le i,j\le m$, $i\ne j$, so that there exist two vertices $v_i,v_j\in E\left(j_n\right)$ such that $r\left(v_i\right|\stackrel{-}{S})=r(v_j\left|\stackrel{-}{S}\right)=(2,2,...,2)$. It should be noted that $\stackrel{-}{S_1}$is not a secure resolving set, which is contrary to assumption. As a result, $sdim\left(E\right(j_n\left)\right)\ge n-4$ is the lower bound. From the above proving, we conclude that $sdim\left(E\right(j_n\left)\right)=n-4$.

Fig. 5Extended jewel graph E(jn )

4. Secure resolving dimension for special classes of graphs

Corollary 4.1 If $G$ is a shadow graph of path $D_2\left(P_n\right)$ of order $n\ge 3$, then $sdim\left(D_2\right(P_n\left)\right)=\frac{n}{2}$.

Corollary 4.2 If $G$ is Jelly fish $J_{n,n}$ of order $n\ge 3$, then $sdim\left(J_{n,n}\right)=n-5$.

Corollary 4.3 If $G$ is Lilly graph $L_n$, $n\ge 5$, then $sdim\left(L_n\right)=\frac{n+1}{2}$.

Corollary 4.4 If $G$ is Twig graph $T{g}_n$, $n\ge 4$, then $sdim\left(T{g}_n\right)=\frac{n+4}{3}$.

Corollary 4.5 If $G$ is Joint sum of two copies of $C_n,$$n\ge 4$, then $sdim\left(G\right)=2$.

Corollary 4.6 If $G$ is quadrilateral graphs $Q_n$, $n\ge 6$, then $sdim\left(Q_n\right)=\frac{n-2}{2}$.

Corollary 4.7 If $G$ is subdividing all the edges of $P_nʘK_1$, $n\ge 7$, then $sdim\left(G\right)=2$.

5. Conclusions

The secure metric dimension of a graph is an NP-complete problem. The present study starts with the task of finding the secure metric dimension of new graph types. The secure metric dimensions of the join of the $(m,n)$ kite graph and the 1-join of the square of the path graph have the same secure metric dimensions. The secure metric dimension of the coconut tree and the extended jewel graph have different secure metric dimensions. Additionally, we deduced the exact formulas for the joint total of two copies of $C_n$, quadrilateral graphs $Q_n$, Jelly fish $J_{n,n}$, Lilly graph $L_n$, Twig graph $T{g}_n$, and subdividing all the edges of $P_nʘK_1$.

In the future, we plan to determine the secure metric dimension of many graphs, such as subdivisions of crown graphs, twig graph, Lilly graph and jelly fish graph. Many other ideas can be inspired from the references [22-25].