A special graph for the connected metric dimension of graphs

1. Introduction

The length of the shortest path between any two vertices in a connected graph $G=(V,E)$, where $V$ is the set of vertices and $E$is the set of edges, is indicated by the distance $d(u,v)$. For any given $b$, the $k$-vector $r\left(v\right|b)=(d(v,b_1),d(v,b_2),...,d(v,b_k))$ is the metric representation of $v$. If there is a unique representation for every pair of $G$ vertices in $r\left(v\right|b)$, then $B$ is a resolving set. Among all the resolving sets of $G$, $dim\left(G\right)$, the metric dimension of $G$, has the least cardinality. A metric basis is a resolving set with low cardinality. Landmarks are the vertices of $G$ on a metric basis.

A minimum resolving set, also known as a metric basis for $G$, is a resolving set that has the smallest cardinality for $G$. The metric dimension of $G$, which is represented as $dim\left(G\right)$. The problem of figuring out the metric dimension of a graph was tackled by Harary et al. [1]. Slater discussed the use of this concept to long-range navigational aids [2]. Melter et al. [3] studied the metric dimension problem of grid graphs. Khulller et al. have also investigated the metric dimension problem for trees and multi-dimensional grids [4]. They also talked about how the idea of metric dimension is used in robot navigation. Note that $G+H$ represents the connecting point of two graphs, $H$ and $G$, and for $n\ge 1$, $f_n=K_1+P_n$ represents a fan. The metric dimension of fan $f_n$ was discovered by Caceres et al. [5]. The Jahangir graph, denoted as $J_{2n}$ with $n\ge 2$, is the graph that is produced from a wheel $W_{2n}$ by removing $n$ alternate spokes. It is also sometimes referred to as the gear graph.

The metric dimension of the Jahangir graph $J_{2n}$, as well as the partition and connected dimension of the wheel graph $W_n$ were calculated by Tomescu et al. [6]. Paths on $n$ vertices constitute a family of graphs with constant metric dimension since Chartrand et al. demonstrated in [7] that a graph $G$ has metric dimension 1 if and only if $G=P_n$. According to Javaid et al. in [8], the planar graph Antiprism $A_n$ is a family of regular graphs with a constant metric dimension such that for any $n\ge 5$, $dim\left(A_n\right)=3$. Ahmad et al. [9] calculated the metric dimension of $P(n,2)ʘK_1$. Sooryanarayana et al. [10] created various types of $r$-sets and determined the minimal cardinality of these sets. Singh et al. [11] computed the metric and edge metric dimensions of the Dutch and French windmill graphs, two types of windmill graphs. Susilowati et al. [12] computed the complement metric dimension of the corona and comb products graphs. Wijaya et al. [13] introduced a simple method for creating new Ramsey minimal graphs from known Ramsey minimal graphs by applying a subdivision operation. A computer program and an algorithm were developed by Muhammad et al. [14] to determine the base and dimension of a network. Rehman et al. [15] gave explicit formulae for the metric dimension of Arithmetic Graph $A_m$ when $m$ has exactly two distinct prime divisors. They gave restrictions on the metric dimension of $A_m$ when $m$ has at least three distinct prime divisors. Feng et al. [16] examined the metric dimension of the power graph of a finite group. The exact value of the metric dimension of Andrásfai graphs was found by Pejman et al. [17]. The constant metric dimension of $P_n(\mathrm{1,2},3)$ and $M_n$ was obtained by Ali et al. [18], while the $k$-metric dimension of linked corona graphs was found to have tight limitations and closed formulas by Moreno et al. [19].

The metric dimensions of a number of graphs, including the Tadpole, Lilly, and special trees (star, bistar, and coconut trees), were ascertained by Mohamed et al. [20]. In addition to giving a summary of several metric dimension findings and uses, Mohamed [21] offered a self-contained introduction to the metric dimension. The tortoise network, the open ladder network, the $Z$-$\left(P_n\right)$ network, and the trapezoid network were among the networks that Mohamed et al. [22] investigated. The connected metric dimension is defined in [23, 24].

In [23], the connected metric dimension of path graph $P_n$, cycle graph $C_n$, wheel graph $W_n$, star graph $K_{1,n-1}$, and complete graph $K_n$ is investigated. It is shown that the connected metric dimension of cycle graph $C_n$,$n\ge 3$ is 2, wheel graph $W_n$, $n\ge 7$ is $⌊\frac{2n+2}{5}⌋+1$, star graph $K_{1,n-1}$, $n\ge 4$ is $n–1$, complete graph $K_n$, $n\ge 3$is $n-1$andpath graph $P_n$, $n\ge 2$ is 2. In [24], it is shown that the connected metric dimension at a vertex of tree $T$is 1 if $v$ is an end vertex and 2 if $v$ is not an end vertex, Petersen graph $P$ is 4, and wheel graph $W_n$, $n\ge 7$ is $⌊\frac{2n+2}{5}⌋+1$. For further information, see the literature [25-37]. This work determines the connected metric dimension of knot graphs, whitehead link graphs and jewel graph. Finally, we derive the explicit formulas for the triangular book graph, quadrilateral book graph and crystal planar map.

2. Definitions and basic terminology

Definition 1. [32] A link $L$ is an embedding of a topological sum of finitely many copies of a circle $S^1$ into three-dimensional topological space $R^3$, $L:S^1\bigsqcup S^1\bigsqcup S^1\bigsqcup ...\bigsqcup S^1\to R^3$. The restriction of $L$ to one of the copies of $S^1$ is called a component of $L$. Note that each component of a link is a Knot.

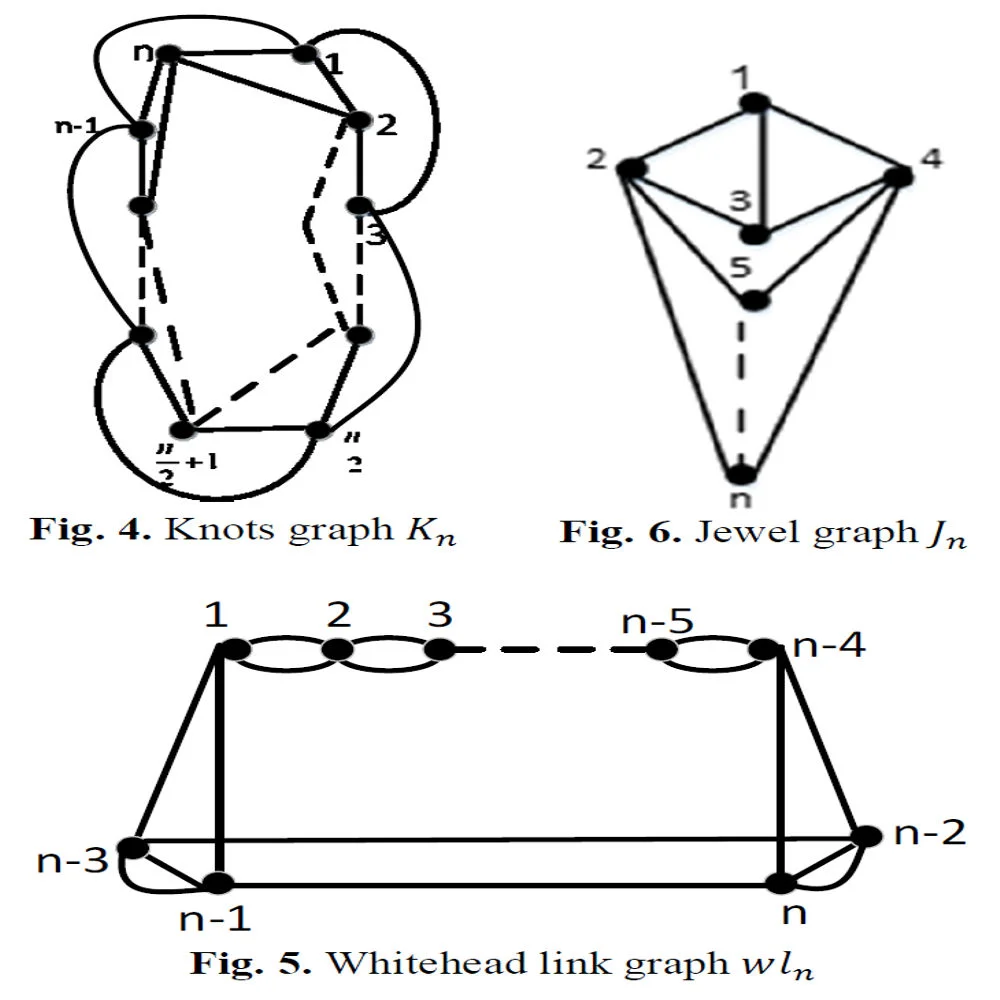
Definition 2. [32] An illustration of a knot or link is a projection of the latter into a plane that shows the markings for each crossing (over- or under-crossing) in the projection’s image. This indicates that a knot diagram is an image of a knot projected onto a plane; a diagram in $R_2$ is composed of several arcs and crossings. It did not permit the following at a crossing where one arc is the over pass and the other forms an under pass.

Fig. 1A diagram of knot or link

Definition 3. [32] A graph of a knot or link diagram is made up of crossings acting as the graphs' vertices and the arcs connecting two crossings acting as its edges.

Definition 4. An alternating knot $A_n$ is a knot with a knot diagram where crossings alternate between overpasses and underpasses. Alternating diagrams are not required for all knot diagrams of alternating knots. All prime knots with seven or fewer crossings are alternating knots, as are the trefoil and figure-eight knots.

We may observe that for $n=7$, every link graph includes at least two multiple edges based on the occurrence of many edges in the graph. In a link graph with an even number of vertices ($n=\mathrm{8,10},\dots$), there are always samples with a single edge. Using the same method as for the 17th-link graph for $n=6$, we can observe this.

Fig. 2Series of link graph starting by chain Borromean ring without any multiple edge

a)$n=$ 6

b)$n=$ 8

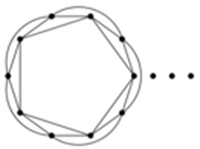
c)$n=$ 10

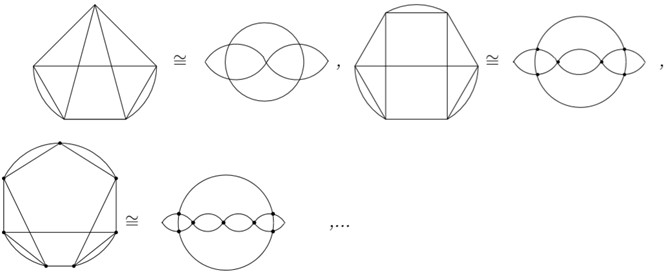
The Whitehead link graph starts the following series of $n$-crossing, $n\ge 5$, 2-component link graphs.

Fig. 3Series of link graph starting by chain Borromean ring

3. Applications of knots graph

First, knot theory provides a wealth of examples for several areas of topology, including geometric group theory and specific types of algebra. The second is a list of scientific and engineering uses, such as separating DNA, combining liquids, and understanding the Sun’s corona structure. Knot invariants arise in many forms, including integers, polynomials, and homology theories.

4. Main results

Corollary 1. Let $G$ is triangular book graph Tn with $n$ vertices, then $cdim\left(T_n\right)=n-2$.

Corollary 2. Let $G$ is quadrilateral book graph $B_n^4$ with $n$ vertices, then $cdim\left(B_n^4\right)=\frac{n}{2}$.

Theorem 3. Let $G$ is Knots graph $K_n$ with $n$ vertices, then $cdim\left(K_n\right)=3$ as shown in Fig. 4.

Proof. We label $K_n$ as shown in Fig. 4. It is clear that the number of vertices is $n$. Let $w=\left\{v_1,v_2,v_3\right\}$. So that the proof has two cases:

Case (1). The representation of the vertices when $n=\mathrm{6,10,14},\dots$ are as follows:

Fig. 4Knots graph Kn

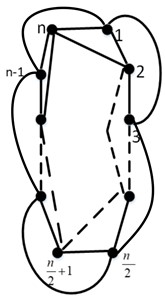
Case (2). The representation of the vertices when $n=\mathrm{8,12,16},\dots$ are as follows:

Clearly, the induced subgraph of $\stackrel{-}{B}$ is connected and the representations of vertices in $K_n$ graph are distinct as shown above, this implies that $\stackrel{-}{B}$is conncted resolving set, but it is not necessarily the lower bound. Hence, an upper bound is $cdim\left(K_n\right)\le 3$. So, we show that $cdim\left(K_n\right)\ge 3$. Let $\stackrel{-}{B}=\left\{v_1,v_2,v_3\right\}$be a connected resolving set with $\left|\stackrel{-}{B}\right|=3$. Assume that ${\stackrel{-}{B}}_1$ is another minimal connected resolving set. If we select an ordered set ${\stackrel{-}{B}}_1\subseteq \stackrel{-}{B}-\{v_i,v_j\}$, $1\le i$, $j\le 3$, $i\ne j$, so that there exist two vertices $v_i,v_j\in K_n$ such that $r\left(v_i\right|\stackrel{-}{B})=r(v_j\left|\stackrel{-}{B}\right)=(\mathrm{1,1},\dots ,1)$. It should be noted that ${\stackrel{-}{B}}_1$is not a connected resolving set, which is contrary to the assumption. As a result, $cdim\left(K_n\right)\ge 3$ is the lower bound. In conclusion $cdim\left(K_n\right)=3$.

Theorem 4. Let $w{l}_n$ is whitehead link graph with $n$ vertices, then $cdim\left(w{l}_n\right)=3$ as shown in Fig. 5.

Fig. 5Whitehead link graph wln

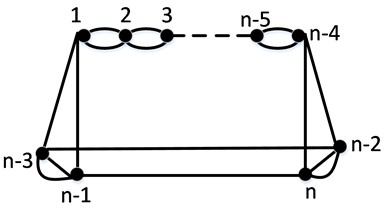
Proof. We label $w{l}_n$ as shown in Fig. 5. It is clear that the number of vertices is n. Let $\stackrel{-}{B}=\left\{v_1,v_2,v_3\right\}$. So that the proof has two cases:

Case (1). The representation of the vertices when $n=\mathrm{7,9},11,\dots$ are as follows:

Case (2). The representation of the vertices when $n=\mathrm{8,10,12},\dots$ are as follows:

Corollary 5. Let $G$ be a crystal planar map $C_n$ with $n$ vertices where $k$ blocks, then $cdim\left(C_n\right)=3$.

Theorem 6. Let $G$ be a jewel graph $J_n$ with $k$ blocks and $n$vertices, then $cdim\left(J_n\right)=2$.

Fig. 6Jewel graph Jn

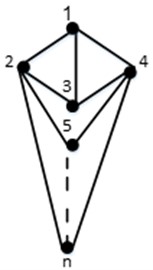
Proof. We label a jewel graph $J_n$as shown in Fig. 6. It is clear that the number of vertices is $n=k+3$ and $k$ is the number of blocks of $G$. Let $\stackrel{-}{B}=\left\{v_1,v_3\right\}$.

Begin

$j=$2

for $i=$ 1: 3

$d\left(v_i,\stackrel{-}{B}\right)=\left(i-1,j\right)$

$j=j-1$

end

for $i=4:n$

$d\left(v_i,\stackrel{-}{B}\right)=\left(\mathrm{1,1}\right)$

end

end

5. Conclusions

Metric dimension is used in many fields, including image processing, combinatorial optimization, robot navigation, network discovery and verification, and wireless sensor network localization. The connected metric dimension of the knots graph, whitehead link graph and jewel graph are determined in this study. Finally, we derived the explicit formulas for the triangular book graph, quadrilateral book graph and crystal planar map.