Finding the domination number of triangular belt networks

1. Introduction

Here, simple, finite, nontrivial, undirected, and connected graphs are all taken into consideration. The task of counting the number of dominating sets in a graph is NP-complete [1]. Domination theory has several applications in chess, security, defence strategies, and wireless communication networks [2]. Dominant sets are also important in many real-world applications, like mobile ad hoc networks and distributed computing [3].

Mohamed et al. [4] looked at the domination number of several networks, such as the linear $k{c}_4$-snake network, bistar network, double fan network, and twig network. In a variety of cycle-related graphs, the locating-total domination number was computed by Raza et al. [5]. Yegnanarayanan et al. [6] calculated a number of Domination values for the Rolf Nevanlinna Collaboration Graph, including Outer Connected Domination, Doubly Connected Domination, Fair Domination, and Independence Domination. The least connected dominating resolving set of graphs was heuristically calculated by Amin et al. [7] using a binary variant of the equilibrium optimisation algorithm (BEOA). Goddard et al. [8] computed two bounds on the $k$-domination number of a graph. Ahangar et al. [9] calculated a variety of constraints on the triple Roman domination number and provided precise values for a few graph families. Martnez et al. proposed new limitations on the double total domination number of graphs [10]. Consult the literature [11-20] for additional information.

In this manuscript, we introduce the domination set of some graphs such as triangular belt networks $TB\left(n\right)$, alternate triangular belt networks $ATB\left(n\right)$ and restricted square of bistar networks $B_{n,n}$.

2. Preliminary notes

Definition 1. Dominating Sets [21]: Any subset of $V$ such that any node out of $D$ is adjacent to at least one node from it is a dominant set $D$ of the graph $G=\left(V,E\right)$. $D\subseteq V$ is formally a dominating set of $G$ if and only if ($\forall v\in$$V\backslash D$) ($\exists u\in D$) ($u$ and $v$ are neighbors).

Definition 2 [22]. Bistar network is the network obtained by joining the root vertices of two copies of star $K_{1,n}$.

Definition 3 [23]. Alternate triangular belt network. Assume that the ladder graph $L_n=P_n\times P_2$ ($n\ge$ 2) has vertex sets $u_i$ and $v_i$, where $i=$ 1, 2,..., $n$. By adding the edges $u_{2i+1}{v}_{2i+2}$ for all $i=$ 0, 1, 2,..., $n-$1 and $v_{2i}{u}_{2i+1}$for all $i=$ 1, 2,..., $n-$1 to the ladder, the Alternate Triangular Belt is formed.

3. Applications of domination number

One area of graph theory that has been studied in great detail is dominance in graphs. One of the fastest-growing areas of contemporary mathematics and computer science is graph theory. A number of factors have led to the development of graph theory as a rather rich and fascinating area of mathematics. Hundreds of research articles on graph theory have been published in the previous thirty years. Mathematicians have given Graph Theory considerable attention in a number of fields. Algebraic Graph Theory, Labeling of Graphs, Matching Theory, Domination Theory, and Coloring of Graphs are a few of these topics.

The theory of domination has been the core of graph theory research recently, and it has a wide range of applications in many domains, including engineering, the physical, social, and biological sciences, linguistics, etc.

Domination emerges in facility location problems, in which the number of facilities (such as fire stations and hospitals) is set and the goal is to reduce the travel time for individuals to reach the closest facility. When the maximum distance to a facility is set and one tries to reduce the number of facilities required to service everyone, a similar issue arises. Land surveying, communication or electrical network monitoring, and difficulties involving selecting groups of representatives all involve concepts from dominance [25-28].

4. Main results

In this section we first give the results of the special cases of Triangular belt networks $TB\left(n\right)$, Alternate triangular belt networks $ATB\left(n\right)$ and restricted square of bistar networks $B_{n,n}$.

Theorem 1 [24]. If and only if one of the following conditions is fulfilled for every vertex $v\in D$ in a graph $G$, then a dominating set $D$ is minimum.

There exist a vertex $u\in V-D$ such that $N\left(u\right)\cap D=\left\{V\right\}$, $v$ is an isolated vertex in $D$.

Theorem 2. The domination number of triangular belt networks $TB\left(n\right)$ is $n-k-1/2$ if $k$ is odd block and $n-k/2$ if $k$ is even block.

Proof. Let the vertices of this network indicated as: $V\left(TB\left(n\right)\right)=\left\{v_1,v_2,v_3,\dots ,v_n\right\}$.

Fig. 1Triangular belt networks TBn

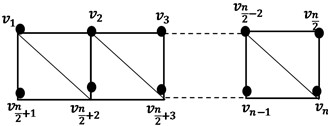
We denoted this network’s dominating set by $S=\{v_1,v_3,v_5,\dots ,v_{\frac{n}{2}-1}\}$. It is evident that $n=2k+2$ is the number of vertices, where $k$ is the number of blocks in $G$.

Case 1. $k$ is odd.

Subcase 1. $i$ is odd.

$r\left(v_1,S\right)=\left(\mathrm{0,2},4,\dots .,\frac{n-4}{2}\right),$

$r\left(v_3,S\right)=\left(\mathrm{2,0},\mathrm{2,4},\dots ,\frac{n-8}{2}\right),$

$r\left(v_5,S\right)=\left(\mathrm{4,2},\mathrm{0,2},4,\dots ,\frac{n-12}{2}\right),$

$⋮$

$r\left(v_{\frac{n}{2}-1},S\right)=\left(i-1,i-3,i-5,\dots ,\frac{n-2}{2}-i\right),$

$r\left(v_{\frac{n}{2}+1},S\right)=\left(\mathrm{1,3},5,\dots ,\frac{n-2}{2}\right),$

$r\left(v_{\frac{n}{2}+3},S\right)=\left(\mathrm{2,1},\mathrm{3,5},\dots ,\frac{n-2}{2}-2\right),$

$⋮$

$r\left(v_{n-1},S\right)=\left(\frac{i-3}{2}.\frac{i-7}{2},\dots ,\mathrm{2,1}\right).$

Subcase 2. $i$ is even.

$r\left(v_2,S\right)=\left(\mathrm{1,1},3,\dots .,\frac{n-6}{2}\right),$

$r\left(v_4,S\right)=\left(\mathrm{3,1},\mathrm{1,3},\dots ,\frac{n-10}{2}\right),$

$r\left(v_6,S\right)=\left(\mathrm{5,3},1,\dots ,\frac{n-14}{2}\right),$

$⋮$

$r\left(v_{\frac{n}{2}-2},S\right)=\left(i-1,i-3,i-5,\dots ,\mathrm{3,1},1\right),$

$r\left(v_{\frac{n}{2}},S\right)=\left(i-1,i-3,i-5,\dots ,i-\frac{n-2}{2}\right),$

$r\left(v_{\frac{n}{2}+2},S\right)=\left(\mathrm{1,2},4,\dots ,i-6,i-4\right),$

$r\left(v_{\frac{n}{2}+4},S\right)=\left(\mathrm{3,1},\mathrm{2,4},\dots ,n-i\right),$

$r\left(v_{\frac{n}{2}+6},S\right)=\left(\mathrm{5,3},\mathrm{1,2},\dots ,n-i\right),$

$⋮$

$r\left(v_{n-2},S\right)=\left(\frac{n-6}{2},\frac{n-10}{2},\frac{n-14}{2},\dots ,\mathrm{1,2}\right),$

$r\left(v_n,S\right)=\left(\frac{i}{2}-1,\frac{i}{2}-3,\dots ,\mathrm{3,1}\right).$

Case 2. $k$ is even.

Subcase 1. $i$ is odd.

$r(v_1,S)=\left(\mathrm{0,2},4,\dots .,\frac{n-2}{2}\right)$

$r(v_3,S)=\left(\mathrm{2,0},\mathrm{2,4},\dots ,\frac{n-6}{2}\right)$

$r(v_5,S)=\left(\mathrm{4,2},\mathrm{0,2},4,\dots ,\frac{n-10}{2}\right)$

$⋮$

$r(v_{\frac{n}{2}},S)=\left(i-1,i-3,i-5,\dots ,\frac{n}{2}-i\right)$

$r(v_{\frac{n}{2}+2},S)=\left(\mathrm{1,2},4,\dots ,\frac{n}{2}-1\right)$

$⋮$

$r\left(v_{n-2},S\right)=\left(\frac{i-4}{2},\frac{i-8}{2},\dots ,\mathrm{1,3}\right),$

$r\left(v_n,S\right)=\left(\frac{i}{2}-1,\frac{i}{2}-3,\dots ,\mathrm{2,1}\right).$

Subcase 2. $i$ is even.

$r\left(v_2,S\right)=\left(\mathrm{1,1},3,\dots .,\frac{n-4}{2}\right),$

$r\left(v_4,S\right)=\left(\mathrm{3,1},\mathrm{1,3},\dots ,\frac{n-8}{2}\right),$

$r\left(v_6,S\right)=\left(\mathrm{5,3},1,\dots ,\frac{n-12}{2}\right),$

$⋮$

$r\left(v_{\frac{n}{2}+1},S\right)=\left(\mathrm{1,3},5,\dots ,\frac{n}{2}\right),$

$r\left(v_{\frac{n}{2}+3},S\right)=\left(\mathrm{2,1},\mathrm{3,5},\dots ,\frac{n-4}{2}\right),$

$⋮$

$r\left(v_n,S\right)=\left(\frac{i}{2}-1,\frac{i}{2}-3,\dots ,\mathrm{2,1}\right).$

Theorem 3. For $k\ge$4, the Alternate Triangular Belt Networks $ATB\left(n\right)$ dominance number is $\left[k/2\right]$.

Initially, we provide this network’s dominating set by a set $S$ where:

$S_1=({v_k}_{+3},v_{k+5},\dots ,v_{2k+1})$ where $n/2$ is odd and $k\ge 2$.

$S_2=(v_k,v_{k+4},v_{k+6},\dots ,v_{2k+1})$ where $n/2$ is even and $k\ge 3$.

The proof is split into two examples for any $v\in S$ that is either $v$ in $S_1$ or $v$ in $S_2$.

Case (1): If $v\in S_1$.

The form 2$k$ always has at least one vertex that is not dominating with any vertex in $S\text{'}$.

So $S\text{'}$ is not dominating set.

So chosen $S$ in this way ensures that there is no proper subset of $S$ dominating $ATB\left(n\right)$.

Case (2): If $v\in S_2$ such that $v=(v_{k+1},v_{k+4},v_{k+6},\dots ,v_{2k+1})$ that mean $v\ne v_1$; also we have always minimum one vertex of the form 2$k$ not dominating with any vertex in $S\text{'}$.

So $S\text{'}$ is not dominating set.

Hence $S$ is minimum.

So $\gamma \left(AT\mathrm{}B\left(n\right)\right)=\left|S\right|=k/2$.

Lemma 1. For $n\ge$ 4, the domination number of restricted square of bistar graph $B_{n,n}$is 2.

We have given the dominating set of this graph as follows: $S=\left(v_1{v}_2\right)$, $S\text{'}=S-v$, $\therefore S$ is minimum, $\gamma \left(B_{n,n}\right)=\left|S\right|=$2.

The minimality of this set is fairly easily demonstrated.

Suppose $S$ is not minimum this suggests that there is an appropriate subset dominating $B_{n,n}$.

If $v\in S$ that is either $v=v_1$ or $v=v_2$.

If $v=v_1$, $v=n/2$, let $S\text{'}=S-v$ we have all the vertices that adjacent to $v$ not dominating with the vertex $v_2=S-v=S\text{'}$.

So $S\text{'}$ is not dominating set.

In the same way, for $v=v_2$.

So selected $S$ in this way guarantees that there is no proper subset of $S$ dominating $B_{n,n}$. $\therefore S$minimum, $\gamma \left(B_{n,n}\right)=$ 2.

5. Conclusions

In this paper, we have invested by determining the dominance set of some graphs such as triangular belt networks $TB\left(n\right)$, alternate triangular belt networks $ATB\left(n\right)$ and restricted square of bistar networks $B_{n,n}$.