Dominator Coloring of Total Graph of Path and Cycle

1. Introduction

Theory of domination and graph coloring are among the most fascinating problems in graph theory, algorithms and combinatorial optimizations. Both the domains are enriched with wide range of research scope in the field of applied sciences. For comprehensive results of coloring and domination in graphs, we refer [1-17] respectively. The domination theory is concerned with a dominating set which requires the minimum set of vertices such that every vertex of a graph not in the set has a neighbor in it while in the concept of graph coloring, it is required to color the vertices using different colors in such a way that both the end vertices of the edge receive different colors. These problems of graph coloring and domination problems are often in relation. These problems are NP hard problems, and they are explored from the point of approximation algorithms [18-22] and parameterized complexity [23-25].

We consider a Graph $G=\left(V\left(G\right),E\left(G\right)\right)$ as a simple, finite, connected and undirected graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. A function $f:V\left(G\right)\to \left\{\mathrm{1,2},\dots .,n\right\}$is said to be proper $n$-coloring of a graph $G$ if $f\left(u\right)\ne f\left(v\right)$ for all $uv\in E\left(G\right)$, where u and v are adjacent vertices in $G$. The smallest integer n for which $G$ admits a proper coloring using n colors is known as the chromatic number $\chi \left(G\right)$. The color class is the group of vertices that share the same color. The set $N\left(v\right)=\left\{u\in V\left(G\right):uv\in E\left(G\right)\right\}$ represents the open neighborhood of $v\in V\left(G\right)$ whereas the set $N\left[v\right]=N\left(v\right)\cup \left\{v\right\}$ represents the closed neighborhood of $v$. Every vertex in a graph $G$that is either an element of $S$ or a neighbor of at least one element of $S$ is refereed as a dominating set. The $\gamma$-set is called the dominating set with minimal cardinality and its cardinality is the domination number $\gamma \left(G\right)$. If each vertex of the graph dominates every vertex of a certain color class then the coloring is said to be dominator coloring. The minimum cardinality of colors used in the graph for dominator coloring is called the dominator chromatic number denoted by ${\chi }_d\left(G\right)$. It is clear that every vertex dominates its respective color class. The total graph $T\left(G\right)$ of $G$ is the graph with the vertex set $V\cup E$ and two vertices are adjacent whenever they are either adjacent or incident in $G$.

Gera et al. [26] presented the idea of dominator coloring. Kavitha and David [27-29] determined the dominator chromatic number for several graph families while Arumugam et al. [30] have thoroughly investigated it. Gera [31] has also explored dominator coloring of bipartite graphs. Merouane et al. [32] analyze the dominator chromatic number of different graph families. Vaidya and Shukla [33] have studied the dominator coloring for degree splitting graphs of various graph families. The dominator coloring of some classes of graphs are obtained by Yangyang Zhou et al. [34]. The dominator coloring of some different graphs is explored by T. Manjula et al. [35]. The dominator coloring of Mycielskian graphs is obtained by A. Mohammed Abid and T. R. Ramesh Rao [36]. The dominator coloring of central and middle graph of some special graphs were investigated by J. Arockia Aruldoss and G. Gurulakshmi [37]. Dominator coloring of regular graphs was derived by T. Manjula and R. Rajeswari [38].

The existing State of art for Various results on some domination coloring of graphs can be found in [39-41]. Chellali and Volkmann [42] found relations between the lower domination parameters and the chromatic number of a graph. The concepts of domination and graph coloring are known to be W-complete [43] and para-NP complete respectively in parameterized complexity. The theory of domination and graph coloring have wide number of applications which led to the algorithmic study of numerous variants of these problems. The algorithmic aspects on dominator coloring of graphs are studied by Arumugam et al. [44].

The objective to find a dominator coloring for graph G is to minimize the number of color classes. Here we outline a significant use of a dominator coloring problem in the social network. To draw a graph of social network, vertices are denoted as social players while the connection between them is shown as edges that is two players are joined by an edge if they are friends. Two strangers can become friends by their mutual friends. Also, each friend wants to serve as a significant mediator for other strangers in order to help them establish interpersonal relationships inside the social network. The dominator coloring problem involves finding the minimum groups of players in the social network with the following characteristics:

1) Players in the same group are strangers.

2) Players in the same group can become friends by at least one common mutual friend.

3) Each player is an intermediary of at least one stranger group.

In the existing literature, the various results on particular graph families are obtained for dominator colorings of graph. Also, certain characterizations, bounds and its properties are discussed for the larger graphs. By the observation of existing literature review, we have obtained the dominator coloring of path and cycle by means of the graph operation as total graph and also, we have proved our results in context of domination number and chromatic number of respective graphs.

These results are useful in terms of bounds of dominator coloring for total graph of path and cycle which can be measured using domination number and chromatic number of a graph. By using these results, one can solve the problem of social networks, channel assignment and time table problem.

Using the presented results, we can solve the problems of standard graph families by means of various graph operations in context of proper coloring and domination number. The new research directions are open for researchers to solve the open problems of dominator coloring for different graph families using various graph operations.

The theory of domination and Graph coloring have various applications in the field of communication, computer, social, biological, air traffic flow network and airline scheduling [45].

2. Preliminaries

Proposition 2.1 [46]

Proposition 2.2 [47]

For any graph $G$, $\chi \left(G\right)\ge 3$ if and only if $G$ has an odd cycle.

Proposition 2.3[48]

For the cycle $C_n$, ${\chi }_d\left[C_n\right]=$$\left\{\begin{array}{ll}⌈\frac{n}{2}⌉,& n=4,\\ ⌈\frac{n}{3}⌉+1,& n=5,\\ ⌈\frac{n}{3}⌉+2,& otherwise.\end{array}\right.$

3. Main Results

Lemma 3.1

Proof:

Let $\left\{v_1,v_2,\dots ,v_n\right\}$ be the vertices of path $P_n$ and let $\left\{u_1,u_2,\dots ,u_n\right\}$ be the newly added vertices corresponding to the edges $\left\{e_1,e_2,\dots ,e_{n-1}\right\}$ of $P_n$ to obtain $T\left(P_n\right)$. Thus $V\left[T\left(P_n\right)\right]=\left\{v_1,v_2,\dots .,v_n,u_1,u_2,\dots ,u_{n-1}\right\}$. The graph $T\left(P_n\right)$ will have $2n-1$ vertices and $4n-5$ edges. Let $S_1=\left\{v_{i\mathrm{}}\in \mathrm{}V\left[T\left(P_n\right)\right]:i\equiv 2\left(\mathrm{m}\mathrm{o}\mathrm{d}5\right)\right\}$ and $S_2=\left\{u_i\in V\left[T\left(P_n\right)\right]:i\equiv 4\left(\mathrm{m}\mathrm{o}\mathrm{d}5\right)\right\}$.

If $n\equiv 0\mathrm{}or\mathrm{}3\mathrm{}\left(\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{}5\right)$ then $S=S_1\cup S_2$ is a dominating set of $T\left(P_n\right)$ and $\left|S\right|=⌈\frac{2n-1}{5}⌉$.

If $n\equiv \mathrm{}1\mathrm{}or\mathrm{}2\mathrm{}or\mathrm{}4\mathrm{}\left(\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{}5\right)$ then $S^{\mathrm{\text{'}}}=S_1\cup S_2\cup \left\{v_n\right\}$ is a dominating set of $T\left(P_n\right)$ and $\left|S^{\mathrm{\text{'}}}\right|=⌈\frac{2n-1}{5}⌉$. Hence $\gamma \left[T\left(P_n\right)\right]\mathrm{}\le ⌈\frac{2n-1}{5}⌉$.

Further since $\gamma \left(G\right)\ge ⌈\frac{n}{\Delta +1}⌉$, it follows that $\gamma \left[T\left(P_n\right)\right]\ge ⌈\frac{2n-1}{\Delta +1}⌉\ge ⌈\frac{2n-1}{5}⌉$.

Thus, $\gamma \left[T\left(P_n\right)\right]=⌈\frac{2n-1}{5}⌉$.

Lemma 3.2

Proof:

Let $\left\{v_1,v_2,\dots ,v_n\right\}$ be the vertices of path $P_n$ and let $\left\{u_1,u_2,\dots ,u_n\right\}$ be the newly added vertices corresponding to the edges $\left\{e_1,e_2,\dots ,e_{n-1}\right\}$ of $P_n$ to obtain $T\left(P_n\right)$.

Thus $V\left[T\left(P_n\right)\right]=\left\{v_1,v_2,\dots .,v_n,u_1,u_2,\dots ,u_{n-1}\right\}$. The graph $T\left(P_n\right)$ will have $2n-1$ vertices and $4n-5$ edges.

Case 1: $\mathit{n}=2$

The graph $T\left(P_2\right)$, contains an odd cycle. According to Proposition 2.2, $\chi \left[T\left(P_2\right)\right]\ge 3$.

By giving the vertices proper coloring as $f\left(v_1\right)=1$, $f\left(v_2\right)=2$, $f\left(u_1\right)=3.$Thus at least three colors are needed for proper coloring. Hence, $\chi \left[T\left(P_2\right)\right]=3$.

Case 2: $\mathit{n}\ge 3$

By Proposition 2.2, $\chi \left[T\left(P_n\right)\right]\ge 3$ as $T\left(P_n\right)$ includes an odd cycle. Assign the proper coloring to the vertices as $f\left(v_i\right)=1,f\left(u_i\right)=3$ for odd $i$ and $f\left(v_i\right)=2,f\left(u_i\right)=4$ for even $i$. Thus, minimum four colors are required for proper coloring. Therefore $\chi \left[T\left(P_n\right)\right]=3$.

Thus, $\chi \left(T\left(P_n\right)\right)=3,\mathrm{}n\ge 2$.

Theorem 3.3

Proof:

We keep using the language and notations from Lemma 3.1.

Case 1: $\mathit{n}=$2, 3, 4, 6

When $n$ = 2

The graph $T\left(P_2\right)\cong C_3$, by proposition 2.3, ${\chi }_d\left[T\left(P_2\right)\right]=3=\chi \left[T\left(P_2\right)\right]+\gamma \left[T\left(P_2\right)\right]-1$.

When $n$ = 3

In this case the vertex $v_2$ is the only one vertex in the $\gamma$-set of graph $T\left(P_3\right).$ According to Lemma – 3.1, $\gamma \left[T\left(P_3\right)\right]=1$ and by Lemma – 3.2, $\chi \left[T\left(P_3\right)\right]=3$. Hence, by giving the vertices of the $\gamma$-set a number of colors equal to $\gamma \left[T\left(P_3\right)\right]$, we define the optimal coloring for $T\left(P_3\right)$.To the remaining vertices of the graph we give $\chi \left[T\left(P_3\right)\right]-1$ number of colors. We denote the coloring pattern as $f\left(v_1\right)=2f\left(v_3\right)=3$, $f\left(v_2\right)=1$, $f\left(u_1\right)=3,f\left(u_2\right)=2$. So every vertex dominates the vertices of at least one color class. A dominator coloring is obtained for the corresponding graphs as a result of this proper coloring. Thus, ${\chi }_d\left[T\left(P_3\right)\right]=4=\chi \left[T\right(P_3)+\gamma [T\left(P_3\right)]-1$.

When $n$ = 4

In this case the set $\left\{v_2,u_4\right\}$ is the only $\gamma$-sets of graph $T\left(P_4\right)$. According to Lemma – 3.1, $\gamma \left[T\left(P_4\right)\right]=2$ and by Lemma – 3.2, $\chi \left[T\left(P_4\right)\right]=3$. Hence, by giving the vertices of the $\gamma$-set a number of colors equal to $\gamma \left[T\left(P_4\right)\right]$, we define the optimal coloring for $T\left(P_4\right)$.To the remaining vertices of the graph we give $\chi \left[T\left(P_4\right)\right]-1$ number of colors. We denote the coloring pattern as $f\left(v_1\right)=3$, $f\left(v_3\right)=4$, $f\left(v_2\right)=1$, $f\left(v_4\right)=3$, $f\left(u_1\right)=4$,f$\left(u_2\right)=3$, $f\left(u_3\right)=2$ so every vertex dominates the vertices of at least one color class. A dominator coloring is obtained for the corresponding graphs as a result of this proper coloring. Thus, ${\chi }_d\left[T\left(P_4\right)\right]=4=\chi \left[T\right(P_4)+\gamma [T\left(P_4\right)]-1$.

When $n$ = 6

In this case the set $\{v_1,v_6,u_4\}$ or $\{v_2,v_5,u_3\}$ are only $\gamma$-sets of graph $T\left(P_6\right)$. According to Lemma – 3.1, $\gamma \left[T\left(P_6\right)\right]=3$ and by Lemma – 3.2, $\chi \left[T\right(P_6\left)\right]=4$. Allocating a number of colors to the vertices of the $\gamma$-set that is equal to $\gamma \left[T\left(P_6\right)\right]$ in order to determine its optimal coloring. Now we use $\chi \left[T\right(P_6\left)\right]-1$ number of colors to color the remaining vertices.

The coloring pattern can be defined as $f\left(v_1\right)=f\left(v_4\right)=f\left(u_2\right)=f\left(u_5\right)=3,f\left(v_3\right)=1,f\left(v_6\right)=f\left(u_1\right)=f\left(u_4\right)=4,f\left(v_2\right)=1,f\left(u_4\right)=2,f\left(v_5\right)=2,f\left(u_3\right)=5.$ Here every vertex dominates the vertices of at least one color class. As a result the proper coloring creates a dominator coloring for the relevant graph. Therefore, ${\chi }_d\left[T\left(P_6\right)\right]=6=\chi \left[T\right(P_6)+\gamma [T\left(P_6\right)]-1$.

Case 2: $\mathit{n}\ge 4$, $\mathit{n}\ne 6$

Let $S_1=\left\{v_i\in V\left[T\left(P_n\right)\right]:i\equiv 2\left(\mathrm{m}\mathrm{o}\mathrm{d}5\right)\right\}$ and $S_2=\left\{u_i\in V\left[T\left(P_n\right)\right]:i\equiv 4\left(\mathrm{m}\mathrm{o}\mathrm{d}5\right)\right\}$. If $n\equiv 0or3\left(\mathrm{m}\mathrm{o}\mathrm{d}5\right)$ then $S=S_1\cup S_2$ be a $\gamma$-set of $T\left(P_n\right)$. If $n\equiv 1or2or4\left(\mathrm{m}\mathrm{o}\mathrm{d}5\right)$ then $S=S_1\cup S_2\cup \left\{v_n\right\}$ be a $\gamma$-set of $T\left(P_n\right)$.

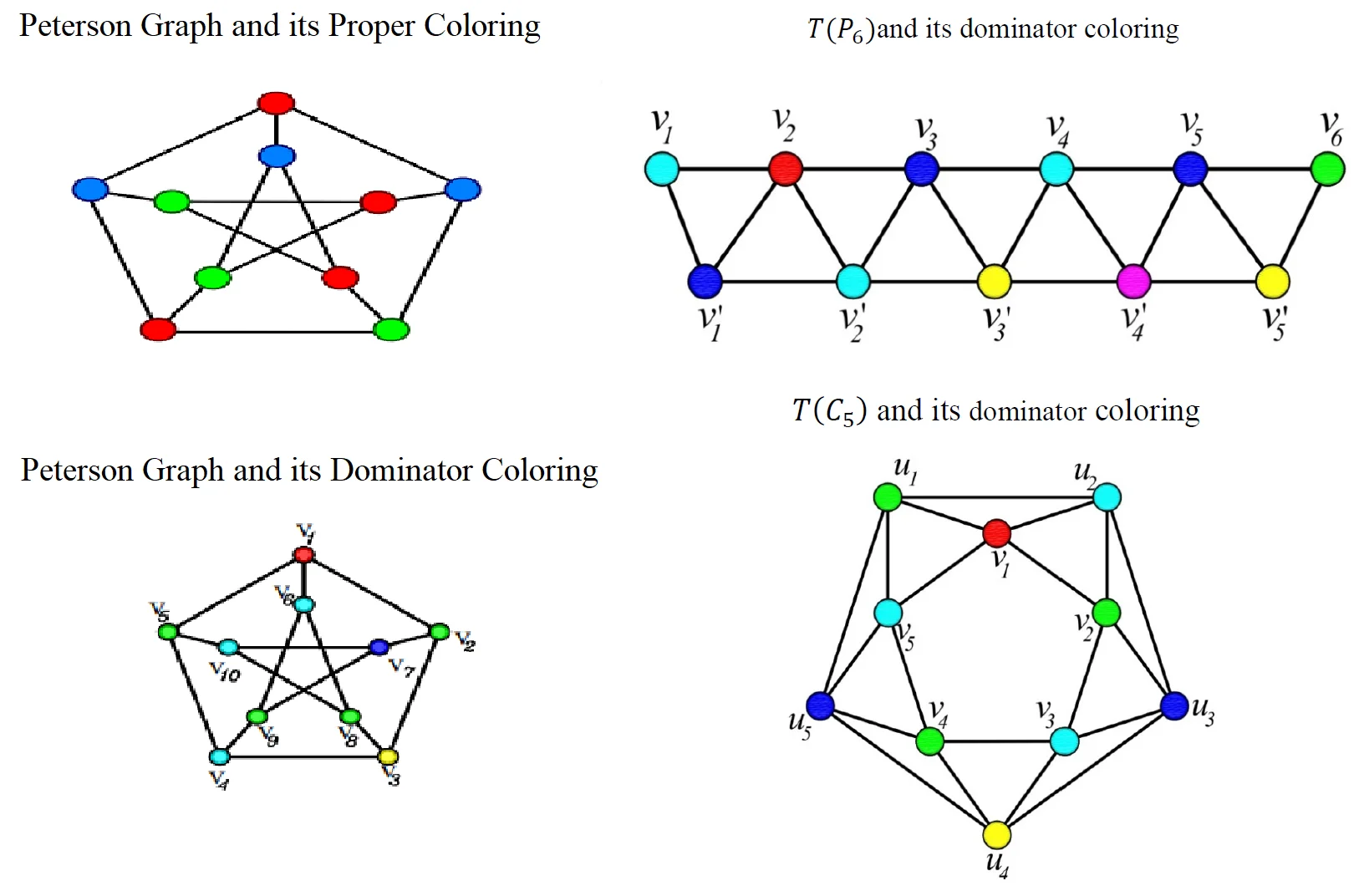
We start the coloring process by giving the vertices of the $\gamma$-set a number of colors equal to $\gamma \left[T\left(P_n\right)\right]$. For the remaining $2n-\left|\gamma \left(T\left(P_n\right)\right)\right|$ vertices assign $\chi \left[T\left(P_n\right)\right]$ number of colors. All the vertices of at least one-color class are dominated by each vertex. This proper coloring pattern satisfies the condition of dominator coloring. Therefore, ${\chi }_d\left[T\left(P_n\right)\right]=\chi \left[T\left(P_n\right)\right]+\gamma \left[T\left(P_n\right)\right]$.

A dominator coloring of $T\left(P_6\right)$ using six colors is shown in Figure – 1

Fig. 1TP6and its dominator coloring

Lemma 3.5

Proof:

Let $v_1,v_2,\dots .,v_n$ be the vertices of cycle $C_n$ and let $u_1,u_2,\dots ,u_n$ be the newly added vertices corresponding to the edges $e_1,e_{2,}\dots ..,e_n$ of $C_n$ to obtain $T\left(C_n\right)$. Then, $\left|V\left[T\left(C_n\right)\right]\right|=2n$ and $\left|E\left[T\left(C_n\right)\right]\right|=4n$.

Case 1: For $\mathit{n}=3$

According to Proposition 2.2, $\chi \left[T\left(C_3\right)\right]\ge 3$ as the graph $T\left(C_3\right)$ has an odd cycle. To give proper coloring to the nodes $f\left(v_1\right)=f\left(u_3\right)=2,f\left(v_2\right)=f\left(u_1\right)=1,f\left(v_3\right)=f\left(u_2\right)=3$. Thus, proper coloring is possible with minimum three colors. Hence, $\chi \left[T\left(C_3\right)\right]=3$.

Case 2: For $\mathit{n}\ge 4$

Using Proposition – 2.2, $\chi \left[T\left(C_n\right)\right]\ge 3$ as the graph $T\left(C_n\right)$ has an odd cycle. To assign proper coloring to the nodes as $f\left(v_n\right)=3,f\left(v_i\right)=1,oddi,f\left(v_i\right)=2,evenif\left(u_n\right)=2,f\left(u_i\right)=3,oddi,f\left(u_i\right)=4,eveni$. By proper coloring at least 4 colors are required. Therefore, $\chi \left[T\left(C_n\right)\right]=4$.

Thus, $\chi \left[T\left(C_n\right)\right]=\left\{\begin{array}{ll}3,& n=3,\\ 4,& n\ge 4.\end{array}\right.$

Theorem 3.6

For $n\ge 3$

Proof:

We continue with the terminology and notations used in Lemma – 3.5.

Case 1: When $\mathit{n}=3$

The set $\left\{v_1,u_3\right\}$ is one of the $\gamma$-set of graph $T\left(C_3\right)$. According to Proposition 2.1, $\gamma \left[T\left(C_3\right)\right]=2$ and by Lemma – 3.5, $\chi \left[T\left(C_3\right)\right]=3$. Hence, by giving the vertices of the $\gamma$-set a number of colors equal to $\gamma \left[T\left(C_3\right)\right]$. We specify the optimal coloring for $T\left(C_3\right)$. Next, we use $\chi \left[T\left(C_3\right)\right]-1$ no. of colors to color code the remaining vertices. The coloring pattern can be summarized as $f\left(v_1\right)=1,f\left(v_2\right)=f\left(u_1\right)=3,f\left(v_3\right)=f\left(u_2\right)=4,f\left(u_3\right)=2$. This coloring meets the requirement for dominator coloring. Thus, ${\chi }_d\left[T\left(C_3\right)\right]=4$.

Case 2: When $\mathit{n}=4$

The set $\left\{v_1,v_3\right\}$ in this instance is a member of the $\gamma$-set of graph $T\left(C_4\right)$. Proposition – 2.1 states that $\gamma \left[T\left(C_4\right)\right]=2$ and Lemma – 3.5 states that $\chi \left[T\left(C_4\right)\right]=4$. As a result, by giving the vertices of the $\gamma$-set a no. of colors equal to $\gamma \left[T\left(C_4\right)\right]$, we specify the ideal coloring for $\left[T\left(C_4\right)\right]$. The remaining vertices are then given colors using $\chi \left[T\left(C_4\right)\right]-1$ no. of colors $f\left(v_1\right)=1,f\left(v_3\right)=2,f\left(v_2\right)=f\left(u_1\right)=3,f\left(v_4\right)=f\left(u_3\right)=4,f\left(u_2\right)=f\left(u_4\right)=5$ are the coloring pattern defined. The dominator coloring requirement is met by this coloring. Therefore, ${\chi }_d\left[T\left(C_4\right)\right]=5$.

Case 3: When $\mathit{n}\ge 5$

Let $S_1=\left\{v_i\in V\left(T\left(C_n\right)\right):i\equiv 1\left(\mathrm{m}\mathrm{o}\mathrm{d}5\right)\right\}$ and $S_2=\left\{u_i\in V\left(T\left(C_n\right)\right):i\equiv 3\left(\mathrm{m}\mathrm{o}\mathrm{d}5\right)\right\}$. Then, $S=S_1\cup S_2$ be a $\gamma$-sets of $T\left(C_n\right)$.

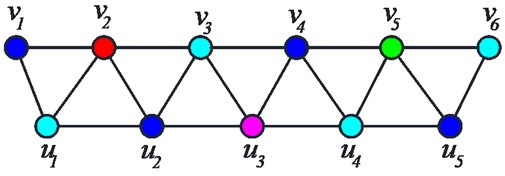
The coloring process is started by allocating the vertices of the $\gamma$-set a no. of colors equal to $\gamma \left[T\left(C_n\right)\right]$. Then using $\chi \left[T\left(C_n\right)\right]-1$ no. of colors, we apply the colors to the remaining $2n-\left|\gamma \left[T\left(C_n\right)\right]\right|$ vertices because each vertex predominates over at least one color class worth of vertices. For the relevant graphs, this proper coloring pattern results in a dominator coloring. As a result, ${\chi }_d\left[T\left(C_n\right)\right]=\chi \left[T\left(C_n\right)\right]+\gamma \left[T\left(C_n\right)\right]-1$.

A dominator coloring of $T\left(C_5\right)$ using five colors is shown in Figure 2.

Fig. 2TC5 and its dominator coloring

4. Concluding Remarks

In graph theory, vertex coloring and theory of domination have many applications in computer and communications network such as cell-phone network, vehicular ad hoc network, wireless sensor network etc. The amalgamation of domination and coloring of graphs called the dominator coloring can be used in the study of interconnections networks. Many research papers are published in the era of dominator coloring in which different authors have discussed about the bounds and the dominator chromatic number of standard graph families whereas in our paper, we have obtained the dominator chromatic number for total graph of path and cycle with the help of chromatic number and domination number. That is the characterization of graphs in two classes as ${\chi }_d\left(G\right)=\chi \left(G\right)+\gamma \left(G\right)$and ${\chi }_d\left(G\right)=\chi \left(G\right)+\gamma \left(G\right)-1$.