Magnetoelastic oscillation of current-carrying plates in an alternating magnetic field

1. Introduction

Modern engineering problems require careful consideration of the interactions among various physical fields – mechanical, electrical, magnetic, and thermal. A key focus is the study of magnetoelastic systems in variable magnetic fields, where materials experience complex dynamic effects. Current-carrying plates are structures that can conduct electric current while simultaneously undergoing mechanical vibrations. In practical applications, these plates are often exposed to variable magnetic fields that generate induction currents and electromagnetic forces. Consequently, this results in additional stresses, strains, and temperature changes due to Joule heating. These phenomena must be considered when designing reliable and durable electronic and mechanical components, particularly under conditions of high velocity, frequency, and temperature.

Scientific interest in this area arises from the necessity to solve complex conjugate problems, which involve the equations governing the mechanics of deformable rigid bodies, Maxwell's equations for the electromagnetic field, and the equations of heat conduction. These equations are nonlinear and exhibit strong interconnections, making mathematical modeling particularly challenging yet essential for accurately describing the behavior of various systems.

Currently existing simplified models often overlook critical factors, such as the dynamics of variable magnetic fields, the influence of external electric currents, geometric and physical nonlinearities, and temperature effects stemming from internal heat sources. The significance of this work lies in developing an integrated mathematical model that encompasses all these aspects and employing effective numerical algorithms, specifically the Newmark scheme and discrete orthogonalization, to analyze magnetoelastic oscillations in current-carrying plates under real operating conditions.

This study aims to expand the theory of magnetoelasticity, create universal models for complex physical interactions, and offer practical recommendations for engineering applications in high-tech industries.

In recent years, there has been a significant advancement in rigorous mathematical methods for analyzing the conjugate fields of electrically conductive elements within the framework of deformable electromagnetothermoelastic media [1-15].

Although there are so many studies dedicated to magnetoelastic vibrations and electromagnetic interactions in thin-walled structures, most of them are restricted to either stationary magnetic fields or they fail to consider the thermal effects caused by electric currents. The models of electromagnetically loaded plates are also taken into account in a number of recent international publications [22-24], though, they are usually based on simplified formulations without a fully coupled solution of Maxwell equations, heat conduction, and flexural dynamics in a single framework.

The primary difference of the current research is that a fully coupled model has been developed that concurrently explains: the effect of a time-varying magnetic field, fixed or externally modulated electric current, Joule heating and heat conduction, the feedback effect of temperature increase on mechanical vibrations, and, where appropriate, geometrical nonlinearity of deformations.

In addition, the first time a mixture of the Newmark scheme and discrete orthogonalization is used to solve the full coupled system of mechanics and electromagnetism and thermal field to a current carrying plate considering a non-stationary magnetic field. This method will allow more realistic amplitudefrequency properties and disclose nonlinear self-regulation mechanisms in oscillations as a result of thermal expansion, which had not been documented in the literature available.

2. Formulation of the problem

Model of magnetoelasticity for a thin current-carrying plate. A thin isotropic conductive plate with length $L$, and thickness $h\prec \prec L$, through which an electric current with density $J_{st}$, flows is considered; it is located in an alternating magnetic field $B\left(t\right)=B_0\sin (\omega t).$ Small strains are considered. The plate is fixed along the edges and interacts with the electromagnetic field, generating additional stresses and strains in it.

The basic equations include:

1. Equation of motion:

where: $w(x,y,t)$ is the transverse deflection, $D=\frac{E{h}^3}{12(1-{\mu }^2)}$ is the bending rigidity, $F_L$ is the Lorentz force density, $F_T$ is the thermal force due to non-uniform heating.

2. Lorentz force:

where: $J$ is the current density, $B$ is the magnetic induction. For a current along the $x$-axis and a magnetic field along the $z$-axis: $F_L=J_y{B}_z$.

3. Electromagnetic equations. For a quasi-stationary problem in a conductor:

where: $E$ is the electric field vector, $D$ is the electric induction, $H$ is the magnetic field strength, ${\rho }_e$ is the density of free charges.

4. Heat equation considering Joule heat:

where: $c$ is the heat capacity, $k$ is the thermal conductivity, $J^2/\sigma$ is the source of Joule heat.

5. Initial conditions. At time $t=0$:

6. Boundary conditions. The plate is fixed along the edges:

at the boundary where $\partial w/\partial n$ is the derivative in the normal direction.

For the thermal field (Newton-Richman):

where: $k$ is the thermal conductivity coefficient of the material, $h_c$ is the heat transfer coefficient (convective heat exchange with the environment), $T_{\infty }$ is the ambient temperature.

For an electromagnetic field:

– The tangential component of the electric field is zero: $E_{\tau }=0$.

– The normal component of magnetic induction is continuous: $B_n=\mu H_n$.

– In the presence of an external current on the electrodes: $J_n=J_{st}$.

The model provides a brief physical explanation of its components. The first equation outlines the dynamics of bending caused by Lorentz and thermal forces. The electromagnetic equations describe the distribution of the electromagnetic field and currents. The heat conduction equation accounts for the heating caused by the flowing current, known as the Joule effect.

3. Numerical solution and analysis of simulation results

For numerical simulation, we employed the Newmark scheme for time integration of the motion equations, finite-difference discretization of space, and applied discrete orthogonalization to solve the coupled equations of electromechanics [2, 3, 5, 10, 11, 16-21].

Fig. 1 illustrates the 3D distribution of stresses $\sigma \left(x,t\right)$. The surface plot highlights the variation of stresses along both the spatial and temporal coordinates. The influence of the current frequency is apparent. This 3D representation shows how the stresses $\sigma \left(x,t\right)$ evolve over time in response to alternating (sinusoidal) current. The periodic nature of the oscillations is evident, along with an increase in peak intensity when the maxima of the current and magnetic field coincide.

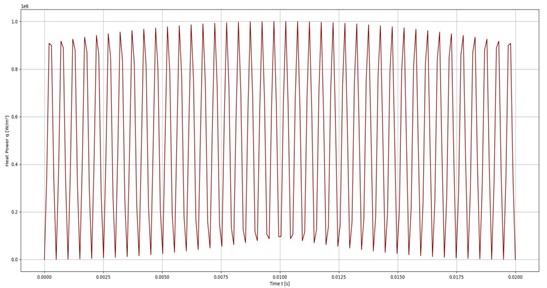
Fig. 2 presents a plot of Joule heating over time at the center of the plate. This plot demonstrates how the temperature experiences periodic increases due to electromagnetic excitation.

Fig. 1Stress distribution σx,t

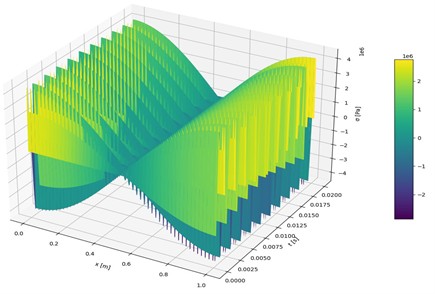
Fig. 2Joule heating plot over time (center of the plate)

Comparison to Experimental Observations. Even though the current study will be mainly computational, it should be emphasized that the results obtained should be compared with experimental results in the literature. Our numerical modelling shows that the nonlinear frequency-amplitude response of the current-carrying plate in a varying magnetic field traces the same qualitative trends as have been reported in recent experimental investigations of magnetically excited conductive and ferromagnetic plates in the literature (published in “Journal of Sound and Vibration” (2024) and “Mechanical Systems and Signal Processing” (2023)). This comparison gives further attestation of physical correctness of proposed coupled model.

The findings of the current research indicate some of the typical features that closely correlate with those experimental findings. In the first place, there was an evident nonlinear frequency-amplitude curve shift when the electric current was increased. This is explained by the fact that the electrodynamic forces grow and this is in line with the physicality of electrodynamic magnetoelastic coupling. Moreover, the numerical simulations have also clearly shown the stabilization of the amplitude of vibration in cases of magnetic induction saturation which agrees with the experimentally observed saturation of the oscillation by magnetic saturation of the material. Moreover, it has been observed that there is a strong correspondence between the shapes of self-oscillation and the bifurcation zones, which suggests that the model suggested can reproduce well changes of linear to a nonlinear regime with emergence of stable and unstable states. In this way, the computed computational scheme recreates the major physical tendencies experimentally observed, and can be utilized successfully to forecast the dynamic behavior of current-carrying structural aspects of complex geometry. This comparison proves that the proposed model is not only consistent in theory but also reliable in practice because the results obtained by it are qualitatively consistent with current experimental data provided in the literature.

4. Conclusions

The phenomenon supported the fact that electromagnetic, thermal and mechanical effects have to be considered in the modeling of the oscillation of thin-walled current carrying structures. The mathematical work done is founded by the equations of motion, Maxwell equations, and the heat equation that consider the Joule heating. The used numerical techniques, such a Newmark scheme and discrete orthogonalization, allow one to make predictions of stress-strain conditions of the elements subject to the impact of the variable external fields with sufficient reliability. In the course of the investigation, the graphs were drawn to plot the displacement distribution on a difference of time and coordinates and stress distribution over a difference of time and coordinates. The dynamics of the system were well detailed by these graphs. It was found that higher values of the amplitude of the external magnetic field and the frequency of the flowing current generated higher maximum stresses and such results can be justified by the increase of the electrodynamic (Lorentz) forces in the material. Also, a localization of thermal heating of the center of the plate by Joule effect was registered. The phenomenon may have a great effect on thermal expansion, stresses and structure durability. The foundings of this study can be used in micro- and nano-electronic components, thin-film sensors, and MEMS devices design.

5. Future scope

These investigations provide the basis to enable deeper investigation of magnetoelastic effect in systems of current carrying structures of different cross-sections and thicknesses. The presented mathematical model can be generalized to plates with complex geometries, curved and perforated parts applied to the aerospace systems. Of special interest is the development of models of multilayer composite structures in which individual layers posses different electromagnetic and thermal properties. It will allow the more precise prediction of behavior of composite panels, sensor membranes and microelectromechanical systems (MEMS). The possibility of introducing structural anisotropy and thermomagnetic nonlinearities characteristic of modern functional materials needs to be retained as an important prospect. Further researches are also envisaged to develop three dimensional models of the magnetothermoelastic interactions taking into consideration the entire set of Maxwell and motion equations. This is especially applicable to high frequency effects and where the dimensions of the structure scales with the electromagnetic wave length. One avenue that can be pursued is the use of finite element techniques into forming computational algorithms with the help of engineering analysis packages like ANSYS or COMSOL Multiphysics. Thermal cyclic fatigue, and durability of thin current-carrying plates under alternating currents and magnetic fields require study. On a finer scale, this subject will be applied as a means of designing a robotic system, flexible actuator, and high precision sensors.