Abstract
This paper presents a study of the stress-strain state and the prediction of the cyclic durability of a set of trolley springs for freight wagons using the finite element modeling (FEM) method in the ANSYS software package. The aim of the study is to evaluate the influence of materials (steel 55Si2 and 60Si2CrVA) on the performance characteristics of springs under static and dynamic loads corresponding to loaded and empty conditions of the wagon. To achieve this goal, parametric 3D models of springs have been created, finite element models have been developed, and strength and fatigue calculations have been performed. The distributions of equivalent stresses and deformations are analyzed, fatigue durability is predicted, and safety margin coefficients are determined. The results obtained make it possible to evaluate the reliability and durability of springs made of various materials in real-world operating conditions, as well as identify critical stress concentration zones.
1. Introduction
Modern freight transportation is the basis of the national economy, providing transportation of a significant part of raw materials, materials and finished products. The reliability and safety of railway transport operations directly depend on the serviceability of its main components and assemblies [1], [2]. One of the most critically important elements of the trolley, bearing the main vibration and shock load, are compression springs (Fig. 1) [3], [4]. Failure of the spring can lead to accidents, serious economic losses and a threat to traffic safety. Therefore, an accurate assessment of the stress-strain state and prediction of the durability of springs are an urgent engineering task [5], [6].
Fig. 1Set of external and internal spring suspension springs

Traditional methods of spring calculation and design, based on analytical formulas and empirical data, often do not fully take into account the complexity of real-world operating conditions, dynamic loading characteristics and the influence of heterogeneity of materials [7], [8], [9]. Experimental tests, although accurate, require significant time and material costs, and are not always available for modeling the entire product lifecycle [10], [11].
In recent decades, the finite element analysis (FEM) method has become a powerful tool for conducting a detailed study of the stress-strain state of complex structures. The ANSYS software package, being one of the leaders in the field of numerical modeling, provides extensive opportunities for creating accurate geometric models, forming computational grids, setting boundary conditions, and performing complex strength calculations, including fatigue life analysis [12], [13].
Despite the widespread use of FEM, there is a need for a systematic study of the stress-strain state and forecasting the cyclic durability of truck springs in freight wagons using modern software tools that take into account the specifics of loads and deformations that occur in real-world operating conditions [14], [15].
The purpose of this study is a comprehensive assessment of the stress-strain state and prediction of the cyclic durability of a set of trolley springs for freight wagons using finite element modeling in the ANSYS software package.
2. Materials and methods
The construction of a solid-state 3D model of a set of external and internal springs was performed in the Autodesk Inventor Professional software package in the compression spring design section. The following input parameters were used: the length of the spring in the free state, the diameter of the wire, the outer diameter of the spring, the number of working turns and the load values. The materials for the springs were steel grades 55Si2 and 60Si2CrVA, the chemical composition of which is given in Table 1.
Table 1Chemical composition of 55Si2 and 60Si2CrVA grade steels [14]
Steel grade | C | Si | Cr | V | Mn | Ni | Cu | S | P | Fe |
55Si2 | 0.52-0.6 | 1.5-2.0 | < 0.3 | – | 0.6-0.9 | < 0.25 | < 0.2 | < 0.035 | < 0.035 | ~ 96 |
60Si2CrVА | 0.56-0.64 | 1.4-1.8 | 0.9-1.2 | 0.1-0.2 | 0.4-0.7 | < 0.25 | < 0.2 | < 0.025 | < 0.025 | ~ 95 |
A comprehensive analysis of the stress-strain state and an assessment of the resource parameters of the springs were performed using specialized software ANSYS 2021 R2, in particular, the Static Structural module. The procedure for dividing a constructive three-dimensional model into discrete elements was implemented by constructing a finite element grid consisting of tetrahedra with an edge length of 5 mm (Fig. 2(a)).
Fig. 2Finite element model of the spring set and boundary conditions

а) Finite element model

b) Boundary conditions at a load of 26460 N

c) Boundary conditions at a load of 9450 N
The boundary conditions determining the mechanical behavior of the structure were set: the complete fixation of the end surface A and the application of external force to the end surface B (Fig. 2(b)). The quantitative values of the applied loads per typical spring set in the design operating modes of a freight car (fully loaded and empty) were 26460 N and 9450 N, respectively (Fig. 2(c)).
3. Results and discussions
The results of numerical analysis under the specified operating conditions are shown in Figures 7-14. The data obtained make it possible to compare the performance characteristics of springs made of different materials and evaluate their reliability in various conditions.
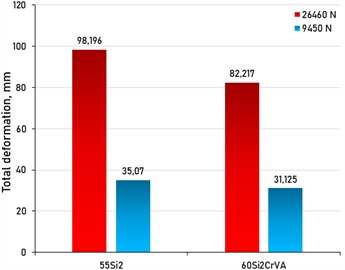
The maximum deformation of springs made of 55Si2 steel reaches 98,196 mm, whereas for 60Si2CrVA steel it is 82,217 mm (Fig. 3), which is ~16 mm less, which indicates a greater elastic compliance of the first set. The lower deformation of 60Si2CrVA steel is explained by a higher modulus of elasticity, which determines the stiffness of the material and its resistance to elastic deformation. The increase in the modulus of elasticity is due to the introduction of alloying atoms that change the interatomic distances in the Fe lattice, as well as the presence of chromium, which further increases this indicator [16]. The maximum equivalent stresses for 55Si2 and 60Si2CrVA steels are 1525.3 and 1498.8 MPa, respectively; at the same time, their conditional yield strengths are 1130 and 1540 MPa, which indicates the possible occurrence of plastic deformation in 55Si2 springs and the preservation of the elastic state in 60Si2CrVA springs. The higher stresses on the inner side of the coils are explained by the shorter length of the inner fibers and the greater amount of their shear during twisting, while the maximum stresses are concentrated in the transition zone from the circular section to the polished end surface.
Fig. 3Analysis of the total deformation of the spring set when a load of 26460 N
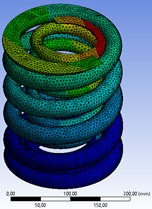
а) 55Si2

b) 60Si2CrVA
Fig. 4Analysis of equivalent stresses acting on the spring set when a load of 26460 N

а) 55Si2

b) 60Si2CrVA
Fig. 5(a) shows that for 55Si2 steel, the zones with the least number of cycles before fracture are concentrated in the upper coil and on the inner side of the spring, while for 60Si2CrVA steel, blue areas predominate (Fig. 5(b)), indicating higher fatigue resistance under the same load. Thus, the spring set made of 60Si2CrVA steel is capable of withstanding up to 10 million loading cycles. Just as in the plots with equivalent stresses, the minimum resource of the springs is observed at the point of transition from the circular section to the support surface. For a set of springs made of 55Si2 steel, the minimum safety margin is 0.37, and for springs made of 60Si2CrVA steel – 0.52 (Fig. 6). These values correspond to the area where the transition to the support surface is observed, since the continuity of the geometry of the spring coil is disrupted. The safety factor of the working coils exceeds one, which ensures the necessary strength of the spring set. At the same time, the obtained values indicate that the spring 60Si2CrVA is more resistant to fracture under a given load than the spring 55Si2.
At a load of 26460 N, the spring deformation is significantly higher than at 9450 N, since greater force causes greater compression: for steel 55Si2, it increases from 35.07 to 98.196 mm, and for 60Si2CrVA – from 31 125 to 82 217 mm, and the difference between the steels is more pronounced at high load (Fig. 7). Equivalent stresses (Fig. 8) are also increasing in the same way: for 55Si2 – from 575.86 to 1525.3 MPa, for 60Si2CrVA – from 544.76 to 1498.8 MPa, and 60Si2CrVA steel experiences slightly lower stresses. The maximum number of cycles before failure (Fig. 9) is achieved at low load (9450 N), while at 26,460 N the service life is shortened due to higher alternating voltages. The safety factor (Fig. 10) at 9450 N for 55Si2 steel is 1.05, and for 60Si2CrVA it is 3.8, which emphasizes the minimum strength of the first and the maximum of the second; the final results are summarized in Table 3 and Fig. 11.
Fig. 5Analysis of cyclic durability of the spring set when a load of 26460 N
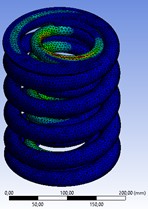
а) 55Si2

b) 60Si2CrVA
Fig. 6Analysis of the safety margin of the spring set when a load of 26460 N

а) 55Si2

b) 60Si2CrVA
Fig. 7Analysis of the total deformation of the spring set when a load of 9450 N

а) 55Si2

b) 60Si2CrVA
Fig. 8Analysis of equivalent stresses acting on the spring set when a load of 9450 N

а) 55Si2
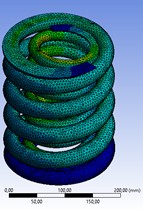
b) 60Si2CrVA
Fig. 9Analysis of the spring set when a load of 9450 N

а) 55Si2

b) 60Si2CrVA
Fig. 10Analysis of the safety margin of the spring set when a load of 9450 N

а) 55Si2

b) 60Si2CrVA
Fig. 11Comparative diagram of the obtained results
а) Total deformations
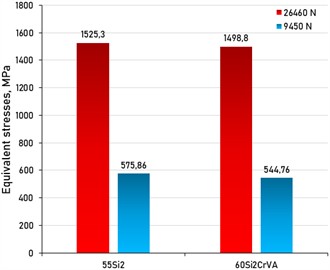
b) Equivalent stresses
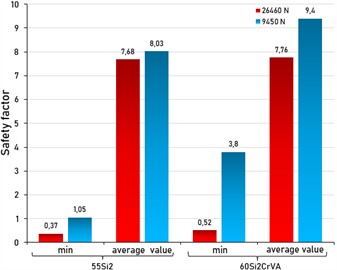
c) Safety margin coefficient

d) Cyclic durability
4. Conclusions
1) The material of the spring significantly affects its performance. Springs made of 60Si2CrVA steel demonstrate higher resistance to deformation and fatigue compared to springs made of 55Si2 steel. This is due to the higher modulus of elasticity and yield strength of 60Si2CrVA steel. Steel 55Si2, under maximum load, can experience plastic deformations, which negatively affects its elastic properties.
2) Critical stress concentration zones have been identified. The greatest stresses and the lowest fatigue life are observed in the transition zone from the circular section to the polished end surface of the coils, which is due to the geometric stress concentration.
3) The durability of springs is predicted depending on the material and operating conditions. Springs made of 60Si2CrVA steel are capable of withstanding up to 10 million loading cycles at maximum load, which significantly exceeds the resource of springs made of 55Si2 steel. When the car is operated in an empty state, the durability of the springs increases significantly for both materials.
4) The evaluation of the safety margin coefficient confirmed the advantage of 60Si2CrVA steel. Springs made of 60Si2CrVA steel have a higher safety margin, which indicates greater resistance to fracture under specified operating conditions.
5) The scientific novelty of this article lies in its comprehensive application of finite element modeling in ANSYS to systematically analyze the stress-strain state and predict the cyclic durability of freight wagon trolley springs under realistic static and dynamic loading conditions, comparing the performance of two distinct spring steels (55Si2 and 60Si2CrVA), identifying critical stress concentration zones, and providing a detailed evaluation of their fatigue life and safety margins, thereby offering a more robust and predictive approach to spring design and reliability assessment compared to traditional analytical or empirical methods.
References
-
V. M. G. Gomes, M. A. V. de Figueiredo, J. A. F. O. Correia, and A. M. P. de Jesus, “Fatigue probabilistic approach of notch sensitivity of 51crv4 leaf spring steel based on the theory of critical distances,” Applied Sciences, Vol. 15, No. 17, p. 9739, Sep. 2025, https://doi.org/10.3390/app15179739
-
N. Tursunov, S. Absattarov, and M. D. Abdulazizovna, “Enhancing the mechanical and functional characteristics of structural spring steel through the advancement of heat treatment technologies,” Vibroengineering Procedia, Vol. 58, pp. 327–332, May 2025, https://doi.org/10.21595/vp.2025.24992
-
S. V. Chunin, E. S. Ohanyan, G. I. Gadzhimetov, M. Y. Balashov, and M. V. Timakov, “Investigation of fatigue strength of spring suspension springs of high-speed freight wagons,” Journal of Transsib Railway Studies, Vol. 2 (54), pp. 42–49, 2023.
-
A. M. Orlova, “Approaches to assessing the stress-strain state of spring suspension springs of freight wagons,” Proceedings of the St. Petersburg University of Railway Communications, Vol. 17, No. 2, pp. 221–232, 2020.
-
A. A. Yagodkin, “Application of finite element methods for optimizing the truck frame of a freight electric locomotive,” in The Role of Innovations in the Transformation of Modern Technology, 2017.
-
N. N. Goldobin and N. V. Eremin, “Mechanical analysis of the folding of a belt spring in the design of a flexible hinge,” Computational Mechanics of Continuous Media, Vol. 15, No. 4, pp. 409–417, 2022.
-
M. Rakhmatov, A. Riskulov, and K. Nurmetov, “Composite materials with enhanced abrasion resistance and certain functional characteristics based on thermoplastics,” Material and Mechanical Engineering Technology, Vol. 2025, No. 2, pp. 86–93, 2025.
-
S. Mamaev, A. Anna, S. Tursunov, D. Nigmatova, and T. Tursunov, “Mathematical modeling of torsional vibrations of the wheel-motor unit of mains diesel locomotive UZTE16M,” in E3S Web of Conferences, Vol. 401, p. 05014, Jul. 2023, https://doi.org/10.1051/e3sconf/202340105014
-
U. T. Rakhimov, N. K. Tursunov, and S. E. Tursunov, “Improvement of production technology for spheroidal graphite cast iron with increased strength,” in Problems in the Textile and Light Industry in the Context of Integration of Science and Industry and Ways to Solve Them: PTLICISIWS-2, Vol. 3045, p. 060024, Jan. 2024, https://doi.org/10.1063/5.0197475
-
A. L. Rutkovskiy, E. M. Bakhteev, Z. G. Salikhov, and M. A. Kovaleva, “An optimized process of drying titanium pellets in a tunnel kiln,” Non-Ferrous Metals, Vol. 2021, No. 5, pp. 89–94, May 2021, https://doi.org/10.17580/tsm.2021.05.12
-
T. M. Tursunov, N. Q. Tursunov, A. P. Kren, T. T. Urazbaev, and U. A. Ziyamukhamedova, “Selection of Geometric Parameters of Indenters that Provide Sufficient Sensitivity to Changes in Characteristics in the Volume of Material,” Material and Mechanical Engineering Technology, No. 2, pp. 72–79, 2025.
-
R. Ghosh, “Static analysis of multi-leaf spring using ANSYS workbench 16.0,” International Journal of Mechanical Engineering and Technology, Vol. 7, No. 5, pp. 241–249, 2016.
-
N. Bekmurzaev, F. Norkhudjaev, and S. Alimukhamedov, “Energy aspects of conjugated heterophase surfaces wear operating in a free abrasive medium,” in Problems in the Textile and Light Industry in the Context of Integration of Science and Industry and Ways to Solve Them: PTLICISIWS-2, Vol. 3045, p. 060018, Jan. 2024, https://doi.org/10.1063/5.0197469
-
“Rods, strips, and coils made of spring-loaded and bearing steel. General technical conditions. – Introduction.,” Standartinform, Moscow, GOST 14959-2016, 2016.
-
V. V. Mylnikov, E. S. Belyaev, D. I. Shetulov, and E. A. Chernyshov, “Influence of heat treatment and loading scheme on fatigue resistance of 60Si2A steel,” International Journal of Experimental Education, No. 10-2, pp. 382–384, 2013.
-
S. N. U. Absattarov and N. K. Tursunov, “The influence of chemical composition, including harmful and undesirable impurities, on the properties of spring-loaded steels,” Universum: Technical Sciences, Vol. 3, No. 12 (129), pp. 5–9, 2024.
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
