Numerical simulation of the spatial distribution of temperature fields in spring elements of freight wagons of railway transport

1. Introduction

The development of modern technologies is impossible without the active use of numerical modeling methods, which play a key role in the design and optimization of processes. Currently, the assessment of temperature conditions during the production of springs is carried out mainly on the basis of an analysis of the microstructural characteristics of the grinders obtained after completion of all stages of the technological process [1], [2]. The main problem is that it is not possible to directly measure and control the temperature distribution in the spring at each processing stage [3], [4]. In this regard, the use of modern computer engineering methods, such as CAE systems (ANSYS), seems to be the most reasonable, since it allows modeling and analyzing temperature fields in a spring in real time, thereby providing more accurate control of technological parameters [5].

Numerical modeling of the distribution of temperature fields in the springs of freight wagons during heat treatment serves as a key tool for optimizing technological modes and ensuring high performance characteristics of products [6], [7]. It allows you to predict the temperature distribution, minimizing internal stresses and deformations, determine the optimal heating and cooling parameters to achieve the required mechanical properties and microstructure, as well as identify areas of potential defects such as cracks or warping [8], [9]. In addition, modeling reduces the cost of experimental research and allows analyzing the effects of various heat treatment parameters, contributing to the development of more efficient and cost-effective technologies [10].

Thus, numerical modeling of the distribution of temperature fields in springs during heat treatment is a key tool for improving product quality, reducing production costs and ensuring the stability of technological processes [11], [12].

The purpose of this work is to develop and apply a numerical model to analyze the spatial distribution of temperature fields in the spring elements of freight wagons in order to evaluate their thermomechanical behavior during heating under quenching, optimize design parameters and increase reliability under operating loads.

2. Materials and methods

The 3D model was built in the Autodesk Inventor Professional software product in the compression spring design section. According to Drawing 9597.50.002 (The drawing was drawn up by the design department of OGK DP “LMZ”, Tashkent), the following input parameters were used: the length of the spring in the free state, the diameter of the wire, the outer diameter of the spring, the number of working turns, the load values, and the properties of the spring material. The spring is made of 60Si2CrVA grade steel, the chemical composition of which is shown in the Table 1. The calculation results indicate that the input parameters are correct. The listed parameters are shown in Table 2 and illustrated in Fig. 1 in the window of the compression spring component generator.

Fig. 1The parameters used to form the geometric model of the spring

a) The loading scheme

b) The digital 3D model of the spring

The temperature field analysis was performed using the ANSYS CAE program in the Transient Thermal subsystem. Transient Thermal Analysis is a research method that makes it possible to evaluate the temporal dynamics of thermal processes in a system under the influence of constant and variable boundary conditions. This analysis makes it possible to determine the time interval required to achieve a stationary thermal state of the system, as well as the duration of maintaining its operational parameters [13], [14]. In the case of variable boundary conditions, the analysis makes it possible to identify the nature of the thermal response of the system and its dependence on temporary changes in external influences [15].

For the reliability of the calculation results, the grid size was 2 mm (Fig. 2). The initial temperature of the product is 22 °C. By default. For 60Si2CrVA steel, heating for quenching is carried out at a temperature of 880 °C [8], which is the final temperature of the spring.

Fig. 2Imported spring geometry and visual inspection of mesh uniformity

In conditions where heat transfer occurs through thermal conduction, the heat exchange process is described by the following differential equation [1]:

where $\rho$ is the density, kg/m³; $c$ is the specific heat, J/(kg∙K); $T$ – temperature, K; $t$ – time, s; $K_x$, $K_y$, $K_z$ – the conductivity of the element in the $x$, $y$, and $z$ directions, W/(m×K); $Q_G$ – heat dissipation capacity per unit volume, W/m³; $v_x$, $v_y$, $v_z$ – the rate of heat transfer in the $x$, $y$, and $z$ directions, m/s.

The boundary conditions are set by convective heat exchange on the surface in accordance with Newton’s law of cooling [1]:

where $q/A$ is the heat flux, J/s; $h_f$ is the heat transfer coefficient, W/(m²×K); $T_s$ is the temperature on the surface of the product, K; $T_b$ is the volume temperature, $K$.

3. Results and discussions

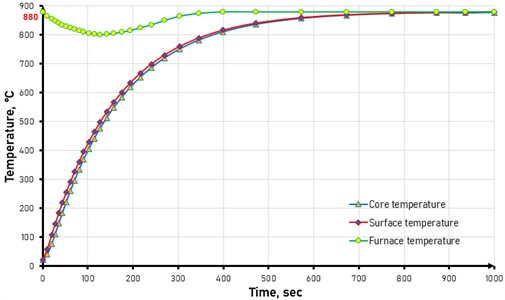
Figs. 3 and 4 show the temperature distribution over the section of the product. The surface temperature after 1000 seconds is 892 °C. The temperature difference between the surface and the core of the product is 1.25 °C. Since the temperature difference is small, the internal stresses during the heating process are minimal. Analyzing the temperature dependence on the heating time (Fig. 4), it can be established that it will take about 900 seconds (15 minutes) to reach the quenching temperature of 880 °C with a rod diameter of 30 mm. The temperature of the furnace after loading the tank begins to drop from 880 to ~800 °C, as heat is absorbed by the tank. The material (cage) loaded into the furnace has a lower temperature than the internal environment of the furnace. When the heaters start working, a significant part of the energy released by them is first spent on heating the tank, which temporarily reduces the average temperature in the furnace chamber.

Fig. 3Temperature distribution over the bar section

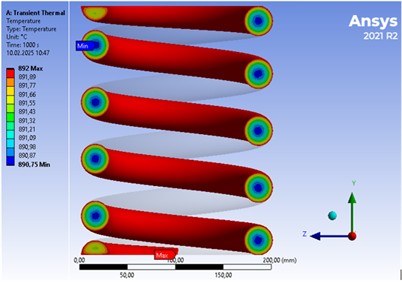
Fig. 4Temperature dependence on heating time

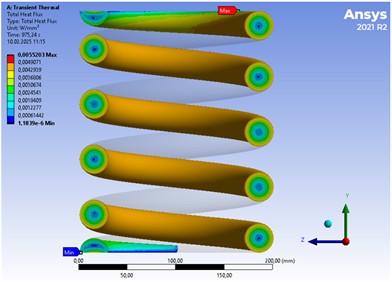
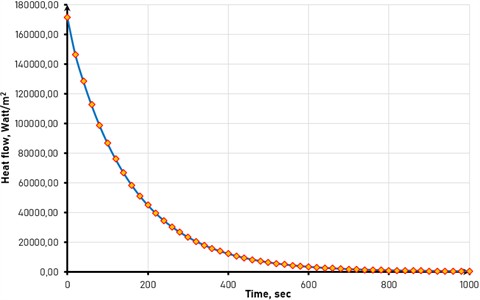
Figs. 5 and 6 show the distribution of the total heat flow over the cross section of the rod. Since the surface temperature is higher during heating than in the core, the heat is transferred deep into the product. The value of the heat flow decreases with increasing heating time, since at the beginning of heating the temperature difference between the surface and the core is maximum, therefore the heat flow is greatest. As the material warms up, this difference decreases, which leads to a decrease in heat flow.

Fig. 5Total heat flow

a) Distribution of the heat flow over the cross section of the spring rod

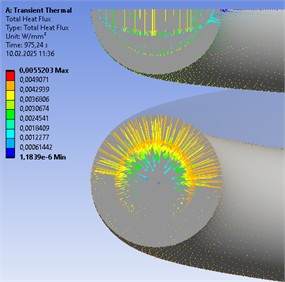
b) Heat flow lines directed inside the product

Fig. 6Dependence of heat flow on heating time

4. Conclusions

1) Optimization of heating modes has shown that it takes about 900 seconds (15 minutes) to reach a quenching temperature of 880 °C in a spring with a diameter of 30 mm. At the same time, the temperature difference between the surface and the core is 1.25 °C, which indicates uniform heating and minimal internal stresses.

2) The heat flow is maximal during the initial heating period, when the temperature difference between the surface and the core is greatest. Over time, the heat flow decreases as the temperature inside the material equalizes.

3) The use of CAE systems (ANSYS) for modeling thermal processes makes it possible to accurately control technological parameters, reduce the cost of experimental research and develop more efficient heat treatment technologies.

4) The scientific novelty of this article lies in its pioneering use of ANSYS-based numerical simulation to precisely model and optimize the spatial distribution of temperature fields in freight wagon springs during heat treatment, enabling real-time analysis that allows for the accurate control of heating and cooling parameters, the minimization of internal stresses and deformations by achieving a minimal surface-to-core temperature difference, the proactive identification of potential defects, and a quantifiable understanding of heat flow dynamics, ultimately contributing to more efficient, cost-effective, and higher-quality heat treatment technologies in the railway transport industry.