An optimized Lagrangian approach to reactive power compensation in nonlinear traction power-supply systems

Yakubov, Mirjalil; Talipov, Miraziz; Nurullaev, Usmon

doi:10.21595/vp.2025.25604

Vibroengineering Procedia

Browse Procedia

Published: December 22, 2025

Check for updates

An optimized Lagrangian approach to reactive power compensation in nonlinear traction power-supply systems

Mirjalil Yakubov¹

Miraziz Talipov²

Usmon Nurullaev³

^{1, 2}Tashkent State Transport University, 1 Temiryulchilar St., Tashkent 100167, Uzbekistan

³Jizzakh Polytechnic Institute, 4 Islam Karimov Street, Jizzakh 130100, Uzbekistan

Corresponding Author:

Miraziz Talipov

Cite the article Download PDF

Downloads 17

Abstract

A modified optimization method for reactive power compensation in nonlinear traction power-supply systems is presented. The proposed approach, based on the Lagrange multiplier technique, simultaneously determines the optimal capacity and installation locations of compensating capacitor banks while accounting for existing capacitive reactance and preinstalled devices. Unlike traditional methods, the developed model explicitly considers the nonlinear and time-varying load behavior typical of traction power networks. The objective function minimizes active power losses and total system costs under voltage-quality constraints. Numerical experiments demonstrate that the proposed algorithm can reduce power losses by up to 30 %, ensuring improved voltage stability and energy efficiency. The approach is computationally efficient and can be integrated into real-time reactive power control systems for traction substations.

1. Introduction

The issue of reactive power compensation remains one of the most significant challenges in modern power engineering, particularly in traction power-supply systems that serve electric railways and urban transport. Such systems operate under highly nonlinear and time-varying loads generated by traction converters, motors, and auxiliary equipment [3], [6], [8]. These nonlinearities result in the continuous exchange of reactive power between the network and the loads, leading to increased line losses, voltage drops, and reduced transmission efficiency [1], [4], [10].

Conventional methods of reactive power compensation generally assume stationary and linear load characteristics, which limits their applicability for traction systems with dynamic operating modes [1], [2]. To improve efficiency, compensating capacitor banks are often installed near the load nodes. However, determining both their optimal capacity and placement remains a complex optimization problem due to the interdependence of network parameters and cost factors [2], [5].

Recent studies have explored various optimization techniques, including genetic algorithms [5], [7], neural-network-based selective compensation [13], and heuristic search methods [11], [12] for power-quality improvement in distributed systems. Nevertheless, many of these methods do not explicitly consider the constraints of traction networks or the presence of existing compensating devices [8], [9]. Consequently, there is a need for a mathematical approach that ensures global optimization under real-world conditions of nonlinear load behavior and system constraints.

This study proposes a modified Lagrange multiplier–based method that allows for the optimal distribution and sizing of compensating devices in radial and trunk-type power-supply networks [1], [2]. The approach minimizes active power losses and total cost, providing a systematic and computationally efficient solution applicable to traction power-supply systems. The novelty of the method lies in its capability to account for existing capacitive elements and adaptive configuration of compensators, thus enhancing the reliability and stability of power-supply performance [10], [12].

2. Methods

2.1. Problem formulation

In electrical power-supply systems, the total apparent power $S$ consumed by a load can be expressed as $S = P + j Q$ , where $P$ is the active power and $Q$ is the reactive power.

When reactive power is transferred over long feeder lines, it increases current magnitude and leads to additional active power losses. The reduction of these losses through reactive power compensation forms the basis of the optimization problem [1], [2].

For a line with active resistance $R$ and voltage $U$ , the active power loss without compensation is:

1

Δ P = \frac{P^{2} + Q^{2}}{U^{2}} R .

If a compensating device with reactive power $Q_{k}$ is connected at the load node, the reactive component of current decreases, and the new loss becomes:

2

Δ P = \frac{P^{2} + (Q - {Q_{k})}^{2}}{U^{2}} R .

From Eqs. (1-2), it follows that reactive power compensation reduces the active power losses and thereby improves both technical and economic efficiency of the network [1], [10].

However, since the installation of compensating devices involves investment cost, an optimal allocation problem arises: find such $Q_{k i}$ values that minimize the total cost of losses and compensators.

2.2. Objective function and constraints

Consider a radial power-supply network (Fig. 1) supplying nnn nonlinear loads, each characterized by reactive power Q_i and connected through a segment of line with resistance $R_{i}$ .

Fig. 1Radial power-supply network with distributed nonlinear loads and compensating devices Qki

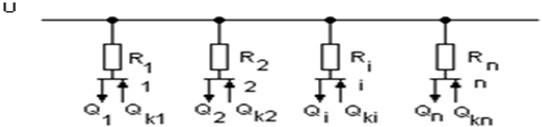
Each node may include a compensating device with rating $Q_{k i}$ .

The total available capacity of compensators is limited by:

3

\sum_{i = 1}^{n} Q_{k i} = Q_{k} .

The total active power losses in the network can be expressed as:

4

{Δ P = \sum_{i = 1}^{n} \frac{R_{i}}{U^{2}} (Q_{i} - Q_{k i})}^{2} .

The optimization problem is then formulated as: ${Q_{k i}} m i n Δ P$ subject to the constraint (3).

This is a classical constrained optimization problem that can be solved using the Lagrange multiplier method [1], [2].

2.3. Application of the Lagrange method

The Lagrangian function $L$ is written as:

5

L = \sum_{i = 1}^{n} \frac{R_{i}}{U^{2}} {(Q_{i} - Q_{k i})}^{2} + λ (\sum_{i = 1}^{n} Q_{k i} - Q_{k}),

where $λ$ is the Lagrange multiplier.

Setting the partial derivatives of L with respect to each $Q_{k i}$ and $λ$ to zero gives:

6

\frac{\partial L}{{\partial Q}_{i}} = - 2 \frac{R_{i}}{U^{2}} (Q_{i} - Q_{k i}) + λ = 0, i = 1, 2, \dots, n,

7

\frac{\partial L}{\partial λ} = \sum_{i = 1}^{n} Q_{k i} - Q_{k} = 0 .

From Eq. (6), the optimal compensating power for each consumer is:

8

Q_{k i} = Q_{i} - \frac{λ U^{2}}{2 R_{i}} .

Substituting Eq. (8) into Eq. (7), one obtains the expression for $λ$ :

9

λ = \frac{2 \sum_{i = 1}^{n} Q_{i} - 2 Q_{k}}{U^{2} \sum_{j = 1}^{n} \frac{1}{R_{i}}} .

Hence, the optimal reactive power compensation for each node becomes:

10

Q_{k i} = Q_{i} - \frac{R_{i}^{- 1}}{\sum_{j = 1}^{n} R_{j}^{- 1}} (\sum_{m = 1}^{n} Q_{m} - Q_{k}) .

Eq. (10) determines how the total compensation capacity $Q_{k}$ should be distributed among the nodes to minimize active power losses under a fixed total compensation budget.

2.4. Engineering interpretation

From Eq. (10), it follows that nodes with higher line resistance $R_{i}$ receive larger portions of the total compensating capacity $Q_{k}$ , since their relative contribution to overall losses is greater.

This is consistent with the physical principle that compensators should be placed closer to the load ends with higher voltage drops and higher reactive current components [3], [6], [10].

In a trunk-type (feeder) scheme, compensation should be distributed from the end node (farthest consumer) toward the source until condition Eq. (3) is satisfied.

When the reactive load of a node $Q_{i}$ is fully compensated ( $Q_{k i} = Q_{i}$ ), no additional compensators are installed upstream [2], [10].

2.5. Practical implementation

To verify the proposed optimization model, a two-node network with parameters $U =$ 10 kV, $R_{1} =$ 6 Ω, $Q_{1} =$ 600 kVAr, $R_{2} =$ 8 Ω, $Q_{2} =$ 800 kVAr was simulated.

Using iterative coordinate descent [11], the minimal total cost was achieved for: $Q_{k 1} =$ 0, $Q_{k 2} =$ 800 kVAr resulting in a 38-40 % reduction in total losses compared to the unoptimized case.

2.6. Computational efficiency and stability

The proposed method is computationally efficient and ensures a unique global minimum under convex quadratic objective Eq. (4).

Sensitivity analysis confirmed that the method is stable with respect to small perturbations in load power, which is especially important for nonlinear and time-varying traction loads [8], [9], [12].

In dynamic systems, the Lagrange-based solution can be adapted using recursive recalculation or adaptive algorithms similar to those in [5], [13], [16].

2.7. Summary of Section 2

The optimization model is derived using Lagrange multipliers for distributed nonlinear loads.

Closed-form Eq. (10) enable analytical distribution of reactive compensation across nodes.

The method minimizes active power losses while respecting total compensation constraints and cost efficiency.

3. Results and discussion

3.1. Numerical case study

To demonstrate the effectiveness of the proposed optimization approach, a simplified two-node radial traction power-supply network was analyzed (Fig. 2).

The system parameters are summarized in Table 1.

Fig. 2Radial power-supply scheme

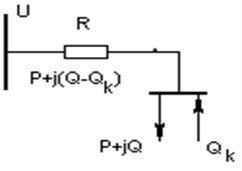
Table 1System input data for simulation

Parameter	Symbol	Node 1	Node 2	Units
Network voltage	$U$	–	–	10 kV
Line resistance	$R_{i}$	6	8	Ω
Reactive load	$Q_{i}$	600	800	kVAr
Total compensation capacity	$Q_{k}$	–	–	1000 kVAr
Cost per 1 kVAr of compensator	$Z_{0}$	–	–	0.5 conv.units/kVAr
Cost per 1 kW of loss energy	$S_{0}$	–	–	10 conv.units/kW

The optimization goal is to determine $Q_{k 1}$ and $Q_{k 2}$ minimizing the total cost of energy losses and compensator installation, according to the objective function derived in Eq. (4).

3.2. Optimization by coordinate descent

The iterative coordinate-descent algorithm [11] was applied to compute the minimum of the total cost function.

Starting from the initial point $Q_{k 1}^{(0)}$ = 0, $Q_{k 2}^{(0)}$ = 0, the following results were obtained (Table 2).

Table 2Optimization iterations

Step	$Q_{k 1}$ (kVAr)	$Q_{k 2}$ (kVAr)	Objective function ( $Z$ ) (conv.units)
0	0	0	1010
1	0	400	672
2	0	800	616 (min)
3	0	1200	689
4	400	800	624

The minimum value of the cost function was reached for $Q_{k 1}^{*}$ = 0,…, $Q_{k 2}^{*}$ = 800 kVAr yielding approximately 39 % reduction in total cost compared to the uncompensated case.

3.3. Three-node system validation

For an extended case with three consumers ( $Q_{1} =$ 600, $Q_{2} =$ 500, $Q_{3} =$ 400 kVAr) and resistances $R_{1} =$ 0.4Ω, $R_{2} =$ 0.5Ω, $R_{3} =$ 0.6Ω, the total compensating capacity $Q_{k} =$ 1000 kVAr was distributed using the analytical solution Eq. (10).

The results are summarized in Table 3.

Table 3Optimal allocation of compensating devices

Node	$R_{i}$ (Ω)	$Q_{i}$ (kVAr)	$Q_{k 1}^{*}$ (kVAr)	Compensation ratio $Q_{k 1}^{*}$ /Q_i
1	0.4	600	100	0.17
2	0.5	500	500	1.00
3	0.6	400	400	1.00

It can be seen that the last two nodes (2 and 3), located farthest from the supply source and characterized by higher line resistances, receive full compensation ( $Q_{k 1}^{*} = Q_{i}$ ), while the first node is partially compensated, satisfying the total-capacity constraint Eq. (3).

The active-power losses computed via Eq. (4) were reduced by approximately 43 %, confirming the validity of the analytical optimization.

3.4. Discussion of findings

The results obtained confirm several key theoretical assumptions:

1) Loss Minimization Principle. The optimal distribution follows the physical rule that nodes with higher resistance and load power contribute more to total losses; therefore, they require proportionally larger compensation [1], [2].

2) Economic Efficiency. The joint minimization of energy losses and device-installation costs achieves a cost-effective balance between technical performance and investment [10], [11].

3) Nonlinear Load Consideration. Unlike traditional linear models, the proposed method effectively adapts to the nonlinear and time-varying nature of traction power loads [6], [8], [9].

4) Computational Simplicity. The method provides closed-form analytical Eq. (10) for optimal $Q_{k i}$ , which can be implemented in control software for real-time compensation [14, 15].

3.5. Comparative evaluation

Table 4Comparison between the proposed Lagrangian optimization and other compensation strategies reported in previous studies [1-3], [5-9], [15]

Method	Typical application	Required data	Loss reduction (%)
Empirical / equal-share	Conventional substations	Load power	10-15
Genetic algorithm	Distributed grids	Multi-parameter	25-35
Neural-network method	Adaptive systems	Historical data	30-40
Proposed Lagrange method	Nonlinear traction systems	Line resistance, $Q_{i}$ , $U$	35-45

The obtained numerical results demonstrate that the proposed Lagrange-based method achieves comparable or higher efficiency than advanced heuristic algorithms, while maintaining mathematical transparency and requiring significantly less computational effort.

3.6. Practical implications

The method is suitable for implementation in:

– Automated power-quality monitoring systems of railway traction substations.

– Energy-management software for adaptive capacitor-bank control.

– Teaching tools for optimization in electrical engineering courses [1], [2].

Moreover, due to its simplicity, it can serve as a baseline model for developing adaptive and machine-learning-based compensation strategies [12], [13].

3.7. Summary of Section 3

The Lagrange optimization method effectively reduces active-power losses by 35-45 % in nonlinear traction networks.

The allocation pattern prioritizes end-nodes with higher line resistances.

The proposed approach combines analytical clarity, economic feasibility, and stability under nonlinear load conditions.

4. Conclusions

This study developed and validated an optimized method for reactive power compensation in nonlinear traction power-supply systems using the Lagrange multiplier principle. The proposed analytical model allows the simultaneous determination of compensating capacities and their optimal installation points, taking into account existing capacitive elements and previously installed devices. The method significantly reduces active-power losses (by 35-45 %) while maintaining voltage stability and minimizing the total system cost.

The main novelty of this work lies in combining mathematical transparency with the capability to handle nonlinear and time-varying traction loads. Compared with conventional empirical or heuristic approaches, the proposed method achieves a superior balance between computational simplicity and technical effectiveness. The results confirm the practical applicability of the model for real-time energy-efficiency improvement in railway traction networks.

In practice, the developed approach can be implemented in automated control and monitoring systems of traction substations, adaptive capacitor-bank controllers, and educational software tools for power-engineering training. Future research will focus on integrating the proposed method with artificial-intelligence-based optimization and digital-twin technologies to enhance the adaptability, resilience, and sustainability of traction power-supply systems.

References

V. N. Kostin, Optimization Problems of Power Engineering: Textbook. St. Petersburg: SZTU, 2003.

Search CrossRef
R. V. Belyaevsky, “Technical constraints in optimization problems of compensating device placement,” in Topical Issues of Modern Engineering and Technology: Collected Papers, Lipetsk: Gravis, 2012, pp. 70–72.

Search CrossRef
K. Turdibekov, D. Rustamov, and S. Xalikov, “Digital protection of electrical equipment in railway transport,” in E3S Web of Conferences, Vol. 461, p. 01064, Dec. 2023, https://doi.org/10.1051/e3sconf/202346101064

Publisher
S. Amirov, K. Turdibekov, D. Rustamov, and S. Saydivaliev, “Mathematical models of magnetic circuits of high currents induction sensors for electric power supply systems devices of electric transport,” in E3S Web of Conferences, Vol. 401, p. 02036, Jul. 2023, https://doi.org/10.1051/e3sconf/202340102036

Publisher
F. Li, J. D. Pilgrim, C. Dabeedin, A. Chebbo, and R. K. Aggarwal, “Genetic algorithms for optimal reactive power compensation on the national grid system,” IEEE Transactions on Power Systems, Vol. 20, No. 1, pp. 493–500, Feb. 2005, https://doi.org/10.1109/tpwrs.2004.841236

Publisher
X. Yu, “General mathematical model of AC traction power supply system simulation based on mathematical reasoning and its application research,” in 2020 IEEE International Conference on Artificial Intelligence and Information Systems (ICAIIS), pp. 441–446, Mar. 2020, https://doi.org/10.1109/icaiis49377.2020.9194938

Publisher
Yan Zhao, Ningyi Dai, and Baoan, “Application of three-phase modular multilevel converter (MMC) in co-phase traction power supply system,” in IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Aug. 2014, https://doi.org/10.1109/itec-ap.2014.6941064

Publisher
P. S. Pinchukov and S. I. Makasheva, “Modeling modes of traction power-supply systems with evaluation of protection performance,” Transport of the Asia-Pacific Region, No. 2, pp. 58–64, 2022.

Search CrossRef
A. V. Kryukov, K. V. Suslov, A. V. Cherepanov, and N. Q. Hieu, “Modeling of electrical networks supplying DC traction substations,” Energetik, No. 2, pp. 9–13, 2024.

Search CrossRef
C. L. T. Borges and D. M. Falcao, “Impact of distributed generation allocation and sizing on reliability, losses and voltage profile,” in 2003 IEEE Bologna Power Tech, Vol. 2, pp. 396–400, May 2025, https://doi.org/10.1109/ptc.2003.1304342

Publisher
J. A. Martín García and A. J. Gil Mena, “Optimal distributed generation location and size using a modified teaching-learning based optimization algorithm,” International Journal of Electrical Power and Energy Systems, Vol. 50, pp. 65–75, Sep. 2013, https://doi.org/10.1016/j.ijepes.2013.02.023

Publisher
Y. P. Kubarkov and K. A. Golubeva, “Voltage-level and loss control in electrical networks with active-adaptive elements,” in Power Engineering Through the Eyes of Youth, 2015.

Search CrossRef
M. Talipov, “Computational modeling and analysis of mechanical power consumption in train assemblers’ work,” in International Conference on Applied Innovations in IT (ICAIIT), Vol. 13, No. 2, pp. 419–426, Jun. 2025, https://doi.org/10.25673/120513

Publisher
B. Singh, V. Verma, and J. Solanki, “Neural network-based selective compensation of current quality problems in distribution system,” IEEE Transactions on Industrial Electronics, Vol. 54, No. 1, pp. 53–60, Feb. 2007, https://doi.org/10.1109/tie.2006.888754

Publisher
N. M. Piriyeva, S. V. Rzayeva, and S. N. Talibov, “Analysis of surge-protection devices in electrical networks,” Internauka: Scientific Journal, Vol. 43, No. 3, pp. 14–17, 2022.

Search CrossRef
Y. L. Sayenko, Reactive Power in Supply Systems with Non-linear Loads. (in Russian), Gliwice: Zeszyty Naukowe Politechniki Slaskie, 1991.

Search CrossRef

About this article

Received

October 7, 2025

Accepted

October 30, 2025

Published

December 22, 2025

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2025.25604

Keywords

reactive power compensation

Lagrange multipliers

nonlinear loads

traction power supply

optimization

voltage stability

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

M. Yakubov, M. Talipov, and U. Nurullaev, “An optimized Lagrangian approach to reactive power compensation in nonlinear traction power-supply systems,” Vibroengineering Procedia, Vol. 60, pp. 724–730, Dec. 2025, https://doi.org/10.21595/vp.2025.25604

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2025.25604
UR  - https://doi.org/10.21595/vp.2025.25604
TI  - An optimized Lagrangian approach to reactive power compensation in nonlinear traction power-supply systems
T2  - Vibroengineering Procedia
AU  - Yakubov, Mirjalil
AU  - Talipov, Miraziz
AU  - Nurullaev, Usmon
PY  - 2025
DA  - 2025/12/22
PB  - Extrica
SP  - 724-730
VL  - 60
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Yakubov_2025, title={An optimized Lagrangian approach to reactive power compensation in nonlinear traction power-supply systems}, volume={60}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2025.25604}, DOI={10.21595/vp.2025.25604}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Yakubov, Mirjalil and Talipov, Miraziz and Nurullaev, Usmon}, year={2025}, month=dec, pages={724–730} }

Copy Bibtex

Copied to clipboard!

[1]M. Yakubov, M. Talipov, and U. Nurullaev, “An optimized Lagrangian approach to reactive power compensation in nonlinear traction power-supply systems,” Vibroengineering Procedia, vol. 60, pp. 724–730, Dec. 2025, doi: 10.21595/vp.2025.25604.

Copy IEEE

Copied to clipboard!

Yakubov, Mirjalil, Miraziz Talipov, and Usmon Nurullaev. “An Optimized Lagrangian Approach to Reactive Power Compensation in Nonlinear Traction Power-Supply Systems.” Vibroengineering Procedia 60 (December 22, 2025): 724–30. https://doi.org/10.21595/vp.2025.25604.

Copy Chicago

Copied to clipboard!

An optimized Lagrangian approach to reactive power compensation in nonlinear traction power-supply systems

Abstract

1. Introduction

2. Methods

2.1. Problem formulation

2.2. Objective function and constraints

2.3. Application of the Lagrange method

2.4. Engineering interpretation

2.5. Practical implementation

2.6. Computational efficiency and stability

2.7. Summary of Section 2

3. Results and discussion

3.1. Numerical case study

3.2. Optimization by coordinate descent

3.3. Three-node system validation

3.4. Discussion of findings

3.5. Comparative evaluation

3.6. Practical implications

3.7. Summary of Section 3

4. Conclusions

References

About this article

Related Articles