Influence of obstacle stiffness on the impact dynamics of a partially fluid-filled spherical shell

1. Introduction

The problems of collision of deformable bodies containing liquid filler are of considerable scientific and practical interest in such fields as aviation and space engineering, vehicle safety, design of protective structures and containers for transportation of liquids [1]-[4]. The peculiarity of such systems lies in the complex interaction of three media – a solid shell, a liquid and an obstacle. The impact produces a non-stationary wave field: elastic and plastic waves in the shell material and pressure waves in the fluid propagate. This interaction determines the actual stress states, deformations and possible loss of stability of the structure. Understanding the mechanisms of fluid-structure interaction under impact loading is critical for ensuring safety and reliability of structures. The presence of a free liquid surface and its inertial motion during impact lead to complex hydrodynamic effects (splashing, hydrostroke), which significantly affect the stress-strain state of the shell. One of the key parameters determining the impact outcome is the mechanical response of the barrier.

In [5] numerical modeling of fluid oscillations in a spherical tank using the method of moving particles is performed. The peculiarities of wave motion of liquid at different modes of excitation – small and large amplitudes of oscillations are studied. It is shown that the moving particle method reproduces well the nonlinear behavior of the fluid, including the formation of splashing and asymmetric wave fronts. The work is useful for estimating dynamic loads on tanks and shells partially filled with liquid, especially under shock or seismic loads.

In [6], analytical models are developed to describe the impact of a solid ball on a spherical shell partially or completely filled with liquid, taking into account the propagation of elastic waves in the shell material. The joint dynamics of a solid, a liquid and a shell under a short-term impulse impact is considered. The study demonstrates that the presence of fluid significantly reduces the local stresses in the wall due to the damping effect, but enhances the overall vibrational behavior of the system. The work is of value for the calculation of thin-walled spherical tanks under impact and the design of strong shells filled with fluid.

In [7], the dynamic behavior of a spherical shell filled with water during impact with a rigid obstacle is studied. Numerical methods based on the coupled hydroelastic model are applied for the analysis. The shell is considered as an elastoplastic material, and the fluid is considered as incompressible, taking into account its inertial effects. It is shown that at high impact velocities the liquid acts as a damping medium, but under certain conditions it can cause local bulging and loss of stability. The work is of practical importance for assessing the strength of tanks, hulls of underwater vehicles and liquid-filled impact systems.

The study [8] is devoted to the influence of fluid vibrations on crack development and stability of spherical tanks under simultaneous action of internal pressure and seismic loads. The methodology is based on numerical modeling in a finite element environment using a crack growth model. The results show that fluid vibrations cause additional unsteady pressure on the tank walls, which accelerates crack development and reduces the critical pressure threshold. At the same time, the interaction of internal waves and structural vibrations can lead to resonant amplification of local stresses. The work provides valuable data for the design of safe tanks used in the chemical and energy industries.

The paper [9] deals with the dynamic loss of stability of spherical shells in underwater collisions. The main attention is paid to the analysis of the behavior of thin-walled metallic shells under the action of a high-speed local impact simulating a collision with a solid body or an object of marine infrastructure. The authors use the finite element method for numerical analysis, taking into account elastic-plastic properties of the material, fluid inertia and contact interactions. The results show that the nature of the shell deformation depends on the thickness to radius ratio and the collision velocity. At high velocities, local buckling and formation of ring waves of deformation are observed, transforming into dynamic loss of stability. At the same time, the surrounding fluid has a damping effect, reducing the amplitude of vibrations but increasing the duration of the transient process.

The purpose of this work is to establish the influence of the obstacle stiffness on the character of dynamic deformation and hydrodynamics of the internal fluid during high-speed impact of a partially filled spherical shell.

2. Task setting and modeling methodology

A system consisting of an aluminum sphere (average radius 15 mm, thickness 2 mm) partially filled with water (segment height 18.05 mm) is considered. The sphere with an initial velocity of 100 m/s collides successively with the lower and upper obstacles, the distance between which is 45 mm (Fig. 1). Gravitational forces were taken into account.

Fig. 1Calculation scheme a) full scheme, b) without the Eulerian zone

a)

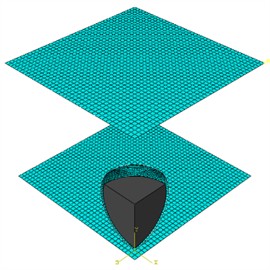
b)

Two cases of obstacle states are considered:

1) The barriers are 2 mm thick elastic steel plates.

2) The barriers are absolutely rigid bodies.

The following output parameters were analyzed: change in vertical diameter of the sphere, the stress-strain state by Mises criterion, displacement of the central points of the barriers and Euler volume fraction for water.

The simulations were performed in the Abaqus/Explicit software package using the Coupled Eulerian-Lagrangian (CEL) approach [10], [11]. This method is ideally suited for fluid-structure interaction problems, especially at large deformations, since it avoids excessive mesh distortion characteristic of purely Lagrangian methods. The spherical shell is modeled in the Lagrangian formulation, while the medium (water and void) is modeled in the Eulerian formulation.

Due to the symmetry of the problem, 1/4 part of the system was modeled with imposition of appropriate boundary conditions. The Eulerian domain was discretized by 8-node linear hexahedral elements with reduced integration and clock mode control (C3D8R). The aluminum shell and elastic plates were modeled using 4-node shell elements with reduced integration (S4R).

The Johnson-Cook plasticity model [12], [13] was applied to describe the behavior of an aluminum shell under high-speed impact. This model adequately describes the dependence of the yield strength of the material on the strain rate and temperature, which is critical in impact interaction problems. In the first case, the barriers were modeled as a linear-elastic material (steel). Water was modeled using the Mie-Grüneisen equation of state (Us-Up), which relates pressure, density, and internal energy and is widely used to describe fluid dynamics under shock loading.

The interaction between the Lagrangian surface of the shell and the Eulerian materials (water) was modeled using the “General Contact” algorithm in Abaqus, which uses a penalty function method to prevent interpenetration.

3. Results and their analysis

Deformation dynamics of the spherical shell. The analysis of the dependences of the change in the vertical diameter of the sphere on time (Fig. 2) reveals cardinal differences between the scenarios.

Fig. 2Comparative plots of vertical sphere diameter variation for a) elastic and b) rigid plates

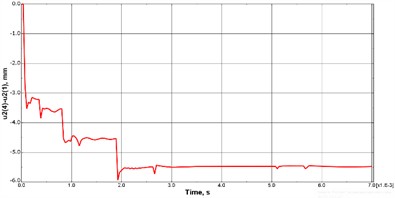
a)

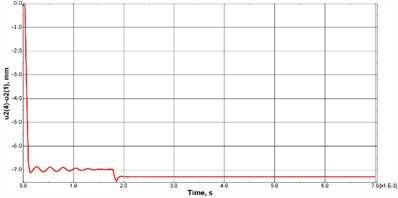
b)

In the presented analysis of the dynamic interaction of an elastic sphere with two parallel plates, a complex sequence of collisions and oscillatory processes is observed. The primary impact of the sphere with the lower elastic plate, recorded at time $t=$0.105 ms, leads to the peak deformation of the sphere, characterized by a decrease in its diameter by the order of ≈ 3.5 mm. This interaction initiates an oscillatory process in the bottom plate. Due to these oscillations, at $t=$0.385 ms, a secondary impact occurs, which increases the maximum deformation of the sphere, whose diameter decreases to ≈ 3.8 mm. Due to relaxation of the stored elastic strain energy, the bottom plate imparts an upward momentum to the sphere, causing it to break away from the surface of the bottom plate. The free motion of the sphere ends at $t=$0.875 ms when it hits the upper plate. This impact induces a larger deformation in which the diameter of the sphere decreases by ≈ 4.7 mm. Similarly, to the previous step, the top plate goes into oscillatory motion, which provokes a second impact on the sphere at time $t=$1.155 ms, increasing the deformation of the sphere, whose diameter decreases to ≈ 4.8 mm. After interaction with the upper plate, the sphere starts moving in the opposite direction. At the moment of time $t=$1.925 ms, another collision with the bottom plate is registered, at which the deformation of the sphere reaches the maximum recorded value, with its diameter decreasing by ≈ 5.9 mm. At this stage, the influence of the internal liquid phase is manifested: the inertial motion of the liquid, which continues to move downward, exerts pressure on the inner surface of the sphere shell. This leads to some reduction of the total deformation, and the diameter reduction is ≈ 5.5 mm. Subsequent impact with the oscillating bottom plate causes a diameter change to ≈ 5.7 mm. Eventually, under the influence of the hydrodynamic pressure of the internal fluid, the diameter strain value stabilizes at ≈ 5.5 mm.

In the case of rigid plates, the first impact results in a strong compression of ≈ 7.0 mm. Rebound is much slower, indicating an almost completely inelastic nature of the impact. Subsequent contact with the top plate slightly increases the deformation to a final residual value of ≈ 7.2 mm.

Thus, interaction with a rigid barrier leads to an increase in the maximum deformation of the sphere by ≈ 22 % and residual deformation by ≈ 31 % compared to an elastic barrier.

Stress-strain state of the shell. The Mises stress field analysis shows that in both cases the stresses exceed the yield stress, which leads to plastic deformation. However, the characters of stress distribution are different.

When the barriers are elastic, the stresses are distributed more smoothly and some of the impact energy goes into the deformation and subsequent oscillation of the elastic plates.

Fig. 3Nature of water behavior at elastic plates

a)$t=$0.42 ms

b)$t=$0.56 ms

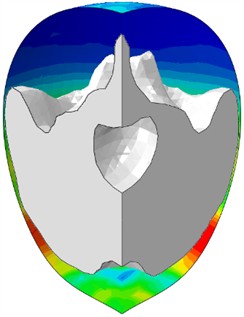
c)$t=$0.77 ms

Fig. 4Nature of water behavior at rigid plates

a)$t=$0.42 ms

b)$t=$0.56 ms

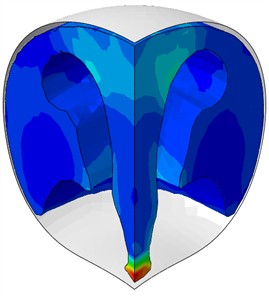
c)$t=$0.77 ms

In the case of rigid plates, an extreme stress concentration in the contact zone is observed. The absence of energy absorption from the barrier leads to the fact that all energy dissipation occurs due to the plastic flow of the shell material, which causes a large deformation depth.

Hydrodynamics of the internal fluid. The behavior of water inside the shell shows the most striking differences.

In the case of elastic plates, with slower and smoother deformation of the shell, the classical splashing effect is observed. Water rises up along the walls, after which its main mass moves by inertia to the upper part of the sphere (Fig. 3).

When the barriers are rigid, due to a sharp and deep deflection of the shell bottom, there is an intensive displacement of the liquid to the center. By the time $t\approx$ 0.42 ms, a deep V-shaped depression is formed on the free surface, indicating the collapse of flows on the symmetry axis. This process immediately precedes the formation of a high-speed cumulative jet, which becomes clearly visible by the time $t\approx$ 0.56 ms (Fig. 4).

4. Discussion of the results

The results clearly illustrate the fundamental role of the barrier in the process of energy redistribution during impact.

When the barrier is considered elastic, the shell-plate system acts as a single damping element. The elastic deformation of the plate “softens” the impact by stretching it over time and absorbing some of the kinetic energy, which is then returned to the system, providing a pronounced rebound.

In the case of a rigid barrier, the shell is the only dissipative element. All kinetic energy of the system must be absorbed by irreversible plastic deformation. This leads to higher local stresses, higher residual strain and almost no rebound. The different strain rate of the shell directly affects the hydrodynamic response of the fluid, changing it from splashing to cumulative jet mode.

5. Conclusions

The numerical study has shown that the stiffness of the barrier is a critical parameter determining the outcome of the high-speed impact of a partially fluid-filled shell.

When impacting an elastic barrier, the shell-plate system functions as a single damping element. A significant part of the initial kinetic energy is absorbed by the elastic deformation of the barrier, which “stretches” the impact impulse in time. This leads to a smoother deformation of the shell and the subsequent return of stored energy, which provides an intense rebound. The internal fluid in this case exhibits classic splashing behavior.

In case of impact against a completely rigid barrier, the shell becomes the only energy dissipating element. The absence of energy absorption from the barrier leads to extremely fast and localized plastic deformation in the contact zone. This causes a significant (31 % more) irreversible shape change and almost complete damping of the rebound. A sharp and deep deflection of the shell bottom provokes a qualitatively different hydrodynamic response – there is a collapse of liquid flows on the symmetry axis with the formation of a high-velocity cumulative jet.

Thus, the results of the work have direct practical significance. When designing protective containers and containers for transportation of liquids, it should be taken into account that the use of external elastic or deformable elements can drastically reduce peak loads and residual deformations on the main container, preventing its destruction. At the same time, the formation of a cumulative jet upon impact with a rigid obstacle may pose a secondary threat, as the jet is capable of producing a concentrated impact on the opposite wall of the shell.