Development of an integrated model for population transport service optimization

1. Introduction

Transportation services are a key area for meeting the population's needs in conducting socio-economic activities. An important direction in improving the quality of transport services and the efficiency of transport enterprises is the application of integrated planning for transportation services for the population using various types of transport. With insufficiently coordinated activities of railway and other types of passenger transport, considering the conditions and principles of organizing passenger traffic [2], there is a need to develop a new integrated approach to transportation services for the population, based on structural-hierarchical and process approaches to the system of developing comprehensive plans, described in [3], [4].

Establishing the optimal level of transportation services in passenger traffic, taking into account the adopted target model, allows for scientifically based planning and modeling of integrated transportation services for the population.

2. Problem statement for modeling comprehensive transport services for the population

Creating models for passenger transportation across a transport network involves considering numerous factors such as passenger transport routes, various types of passenger transport, travel time, and transportation cost.

The parameters of the passenger transport model include: $N$ is the total count of transport network nodes, including railway stations and stops; $M$ is the variety of transportation types involved, such as trains, buses, and metro; $C_{ij}$ is the expense incurred to move a passenger from point i to point $j$; $T_{ij}$ is the time of transporting a passenger from point $i$ to point $j$; $T_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum allowable transportation time for a passenger from point $i$ to $j$; $P_{ij}$ is the route capacity between nodes $i$ and $j$; $D_{ij}$ is the demand for passenger transportation between nodes $i$ and $j$.

The passenger transport model variables include: $x_{ij}^k$ is the number of passengers transported between nodes $i$ and $j$ by transport type $k$ [5].

The model’s objective function may differ based on its intended purpose.

To reduce overall transport expenses, the objective function is defined as:

The travel time minimization objective function is formulated as:

The function aiming to minimize overall transport costs and passenger travel time can be represented as:

where α corresponds to the cost weight and $\beta$ to the weight of travel time in the objective function.

The constraints in the passenger transportation model across the route network using various types of transport include:

– Demand constraints (each direction must be satisfied cumulatively by all types of transport): $\sum _{k=1}^M{x}_{ij}^k=D_{ij}$, $\forall i,j$.

– Capacity constraints (the number of passengers transported on each route should not exceed its capacity): $x_{ij}^k\le P_{ij}^k$, $\forall i,j,k$.

– Non-negativity constraints (the number of transported passengers cannot be negative): $x_{ij}^k\ge 0$, $\forall i,j,k$.

– Maximum travel time constraints (travel time should not exceed the maximum allowable time): $\sum _{k=1}^M{T}_{ij}^k{x}_{ij}^k\le T_{max}$, $\forall i,j$.

In its full formulation, the passenger transport model over the route network using different types of transport is expressed as follows:

under the conditions: $\sum _{k=1}^M{x}_{ij}^k=D_{ij}$, $\forall i,j$; $x_{ij}^k\le P_{ij}^k$, $\forall i,j,k$; $x_{ij}^k\ge 0$, $\forall i,j,k$; $\sum _{k=1}^M{T}_{ij}^k{x}_{ij}^k\le T_{max}$, $\forall i,j$.

This model is basic and can be supplemented with other parameters and constraints depending on the specific tasks and conditions of the transport network.

3. Modeling the transportation service system for the population using graph theory

Addressing the problem of providing transportation services to the population through graph theory entails identifying optimal routes and allocating passenger flows along them. To achieve this, the transport network is modeled as a directed graph $G=\left(V,E\right)$, where $V$ is denotes the set of vertices (nodes) corresponding to stations, stops, and other elements of different passenger transport modes, and $E$ is represents the set of directed edges (arcs) indicating the available routes between these nodes.

In general, the graph has the form presented in Fig. 1 and reflects the transportation of passengers by rail and road transport over the network of railways and roads [5]. It is a multigraph as it contains multiple edges incident to the same pair of vertices (stops).

Its purpose is to conceptually demonstrate the transport network structure modeled as a directed multigraph $G\left(V,E\right)$, where vertices represent transport nodes (stations, stops) and edges represent available routes. The figure illustrates the logical structure of multimodal connectivity (road and rail), serving as a universal example applicable to any city network.

Fig. 1A schematic illustration of the transport network graph

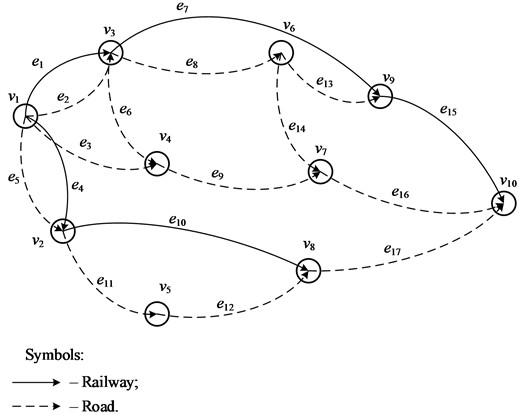
Each arc $e\in E$ of the graph is associated with:

– The cost of transporting a passenger along arc $e$ – $C\left(e\right)$.

– The time of transporting a passenger along arc $e$ – $T\left(e\right)$.

– The capacity of the route – $P\left(e\right)$.

– The demand for passenger transportation – $D\left(e\right)$.

– The number of passengers transported along the arc – $x\left(e\right)$.

The problem is formulated as a maximum flow problem with the minimal cost and travel time for passengers on a graph, where it is necessary to find such flows $x\left(e\right)$ along the arcs to:

– Minimize the total transportation cost.

– Minimize the travel time for passengers.

– Satisfy all demand, capacity, and time constraints.

The problem is formulated as a minimum-cost flow problem on a directed graph, where the objective is to determine flow values $x\left(e\right)$ along the arcs such that:

– The total transportation cost is minimized.

– Passenger travel time is minimized.

– All demand, capacity, and time constraints are satisfied.

When applying graph theory to solve the cost minimization problem, the objective function is formulated as follows:

under the conditions$\sum _{e\in {\delta }^{+}\left(v\right)}x\left(e\right)-\sum _{eϵ{\delta }^{-}\left(v\right)}x\left(e\right)=b\left(v\right)$, $\forall \mathrm{v}\mathrm{ϵ}\mathrm{V}$ (meeting transportation demand); $0\le x\left(e\right)\le P\left(e\right)$, $\forall e\in E$ (capacity constraint), where ${\delta }^{+}\left(v\right)$ is the set of outbound connections from node $v$; ${\delta }^{-}\left(v\right)$ refers to the set of inbound connections to node $v$; $b\left(v\right)$ is the net transportation demand at node $v$, where positive values indicate supply (sources) and negative values indicate demand (sinks).

To solve the minimum cost flow problem, various algorithms can be used:

– Least Cost Method: the least cost path is selected, and the flow along this path is increased until all constraints are met.

– Potential Method: updating vertex potentials enables the search for cost-optimal paths.

– Ford-Fulkerson Algorithm: used to find the maximum flow and then modified to minimize cost.

If time constraints need to be taken into account, the problem becomes multicriteria:

under conditions:

The solution to such a problem involves finding such flows $x\left(e\right)$ on the graph $G$, which minimize the total transportation cost, meet the demand for transportation, do not exceed the route capacity, and comply with time constraints.

The task of minimizing transportation costs and passenger travel time through graph theory can be framed as a multicriteria optimization problem. Accordingly, the objective function that reflects both total cost and travel time minimization, as expressed in Eq. (3), is formulated as follows:

here $\alpha$ and $\beta$ are coefficients that determine the importance of cost and time, respectively.

To find a solution to such a multicriteria problem, we use minimum cost flow algorithms adapted to consider two criteria, such as:

1. Least Cost Algorithm. Solution sequence:

– Set initial values of the variables $x\left(e\right)$ for all arcs $e$.

– To find the optimal path with the minimum combined weight, a tailored Dijkstra or Bellman-Ford algorithm is used [weight = $\alpha C\left(e\right)+\beta T\left(e\right)$].

– Find the least cost path. Update $x\left(e\right)$ values along the found path. Check all constraints.

– Repeat the steps until an optimal flow is found or all constraints are met.

2. Potential Method. Solution sequence:

– Set initial vertex potentials and values of the variables $x\left(e\right)$.

– Use an algorithm to find cycles with a negative sum of weighted values [weight = = $\alpha C\left(e\right)+\beta T\left(e\right)$].

– If a negative cycle is found, update vertex potentials and $x\left(e\right)$ values.

– Adjust $x\left(e\right)$ values according to the found cycles.

– Repeat the steps until all negative cycles are found.

Thus, the passenger transportation model across the route network using various types of transport is based on graph theory methods. The use of this model facilitates optimal passenger flow assignment across the transport network, respecting all given parameters and constraints. To solve the problem of minimizing transportation costs and passenger travel time using network flow optimization algorithms, the least cost algorithm is adopted. This algorithm allows minimizing both costs and travel time for passengers by creating optimal routes that meet economic and time constraints. It considers parameters such as route capacity and transportation demand, making it a versatile tool for various conditions. By optimally distributing resources and routes, the overall efficiency of the transport system is increased, reducing costs and increasing profitability. Ultimately, this improves the quality of passenger services, reduces waiting time, and contributes to the sustainable development of transport infrastructure.

4. Model for integrated passenger transport services via rail and road modes

To formulate the model of integrated passenger transportation services via rail and road transport – taking into account both carrier route organization costs and passenger waiting costs – we define the following parameters on the arcs [6]: $C_{ij}^{\left(\alpha \right)}$ is the passenger transportation cost by road transport between nodes $i$ and $j$; $C_{ij}^{\left(r\right)}$ is the passenger transportation cost by rail transport between nodes $i$ and $j$; $T_{ij}^{\left(\alpha \right)}$ is the passenger transportation time by road transport between nodes $i$ and $j$; $T_{ij}^{\left(r\right)}$ is the passenger transportation time by rail transport between nodes $i$ and $j$; $P_{ij}^{\left(\alpha \right)}$ is the road transport route capacity between nodes $i$ and $j$; $P_{ij}^{\left(r\right)}$ is the rail transport route capacity between nodes $i$ and $j$; $D_{ij}$ is the passenger transport demand between nodes $i$ and $j$; $d_{ij}$ is the length of the route connecting nodes $i$ and $j$ [5]; $R$ is coverage area (the maximum allowable distance between the passenger transport stop and the settlement within the service area of this stop); $W_i$ is average passenger waiting time at node $i$; $C_w$ is the cost of passenger waiting time (in monetary equivalent per unit of time).

The variables in this model of integrated passenger transportation services by road and rail transport include: $x_{ij}^{\left(\alpha \right)}$ – the passengers number transported by road transport between nodes $i$ and $j$; $x_{ij}^{\left(r\right)}$ – the passengers number transported by rail transport between nodes $i$ and $j$ [5].

To minimize the overall cost comprising transportation planning and passenger waiting, the objective function is given by:

The constraints governing the integrated rail and road passenger transportation model are defined as follows:

– Demand constraint: $\sum _{j\in V}\left(x_{ij}^{\left(\alpha \right)}+x_{ij}^{\left(r\right)}\right)=D_{ij}$, $\forall \left(i,j\right)\in V$.

– Capacity constraint: $0\le x_{ij}^{\left(\alpha \right)}\le P_{ij}^{\left(\alpha \right)}$, $\forall \left(i,j\right)\in E$.

– Non-negativity constraint: $0\le x_{ij}^{\left(r\right)}\le P_{ij}^{\left(r\right)}$, $\forall \left(i,j\right)\in E$.

– Waiting time constraint: $W_i\ge 0$, $\forall \mathrm{i}\in \mathrm{V}.$

– Distance constraint considering the coverage area: $d_{ij}\le R$, $\forall \left(i,j\right)\in E.$

In general, the complete model of integrated passenger transportation services by road and rail transport is described as:

under the conditions:

When automated implementation of the obtained model is performed, the solution can be obtained using optimization methods, such as linear programming or multicriteria optimization methods. The presented model takes into account both transportation organization costs (cost and capacity) and passenger waiting costs, making it more applicable for modeling transport systems.

Predictive dependencies can be implemented in specialized software environments for forecasting and optimization, such as Python or AnyLogic. The predictive model of integrated transport services for the population provides a basis for long-term planning of transport services and allows accounting for dynamic changes in all aspects of the transport system.

5. Conclusions

The scientific novelty of our study lies in the development of an integrated multimodal optimization model that simultaneously:

1. Combines rail and road transport systems within one mathematical framework.

2. Minimizes both organizational transport costs and passenger waiting-time costs.

3. Incorporates forecasting capabilities for long-term transport planning.

This dual-criteria approach differentiates our model from earlier single-mode cost-minimization models and provides a foundation for automated, predictive transport system optimization.

The results of the verification of the provisions of the proposed model of integrated transport services for the population are described in [7].

Thus, the authors of the article created a tool to optimize the transport service system by sequentially minimizing transportation organization costs and passenger waiting time costs. The solutions allow automating the modeling of transport systems using the developed model of integrated transport services for the population. The necessary patterns of passenger flow changes are described and obtained, allowing the proposed model to be used for forecasting the state of the transport system when systematically changing its load or transforming its structure.