Seismic performance evaluation of high ground stress soft rock tunnels using incremental dynamic analysis

1. Introduction

Soft rock tunneling is difficult especially under high ground stress conditions resulting in possible instability caused by stress variations in the tunnel lining [1, 2]. In addition, tunnels are prone to varying forms of seismic risks that exert greater pressure than otherwise [3, 4]. Hence, the seismic design of soft rock tunnels under high ground stress is important for improving their stability during earthquakes [5, 6].

High ground stress soft rock tunnels are an important topic in the current engineering practice especially in seismically active regions which require seismic investigation [7, 8]. The response of tunnels to ground movement caused by tunnels due to earthquakes is not an easy task. To ensure safety, tunnels should be subjected to seismic investigations to ensure the safety of both the structure and its users [9, 10]. The consequences of tunnel failure can have severe consequences such as loss of lives, property destruction as well as financial loss [3].

To ensure the safety and stability of high ground stress soft rock tunnels under seismic loading, seismic analysis is required for their design and construction [11, 12]. Tunnel linings can be significantly damaged by seismic activity, which can lead to failure and collapse [6, 13]. High ground stress soft rock tunnels are difficult to study because of the complex processes surrounding the interaction of the rock mass and tunnel lining under seismic loading [4]. Soft rock tunnels are particularly vulnerable to seismic damage because of their low stiffness and high ground stress levels [14, 15].

The growing need of transportation systems, water delivery, energy sources, and utility of the urban areas has driven the intensive use of underground buildings, more so tunnels as the most viable infrastructure in the populated and hilly areas [16-19]. Rapid urbanization and the population increase have also contributed to the intensified use of subsurface space where the surface space turns out to be limited and expensive [20, 21]. Seismic safety is a vital design factor in tunnels because of the seismic activity not only in terms of high in-situ ground stresses but also, dynamic loading due to the occurrence of earthquakes in the area [3]. True to their name, the underground tunnels are in direct contact with the surrounding soil or rock mass, which means that their seismic behavior is determined by non-trivial mechanisms of soil-structure interaction, which require special analytical and numerical methods to be able to assess their performance reliably [12, 22].

Similar to any other type of civil engineering design, the goal of seismic design is to offer the structure the ability to withstand the loads, displacements, and deformations that are applied to it [9]. Calculating how a building or other structure will react to earthquakes is called seismic analysis, which is a subset of the structural analysis. Because the initial criteria for seismic engineering were only defined at the start of the 20th century and the majority of key contemporary concepts only emerged in the previous 50 years, seismic engineering is a relatively recent field of structural engineering [10]. Seismic issues with underground structures are frequently disregarded, even though this cannot be used to justify ignoring seismic action [23-26]. This is because the seismic performance of underground structures is generally believed to be superior to that of surface structures.

Although tunnels often outperform aboveground structures during earthquakes, the damage to some significant structures during earthquake events, such as the 1995 Kobe earthquake in Japan, 1999 Chi-Chi earthquake in Taiwan, 1999 Bolu earthquake in Turkey, 2004 Baladeh earthquake in Iran, 2004 Niigata earthquake in Japan and most recently, the 2008 Sichuan earthquake in China, has highlighted the need to account for seismic loads in the design of underground structures [27-30].

In that regard, the current research seeks to assess seismic behavior of high ground stress deep-buried soft rock tunnel by applying Incremental Dynamic Analysis (IDA) framework. A two-dimensional numerical model is constructed in MIDAS GTS NX to examine the nonlinear seismic behavior of the tunnel due to escalating earthquake levels. The analysis targets the primary parameters of engineering demands, such as the displacement, base shear, and drift ratio, and the fragility analysis is used to measure the likelihood of exceeding the damage during moderate and strong seismic motions. The outcomes are aimed to give the evidence of the vulnerability of soft rock tunnels and help the implementation of the performance-based seismic design techniques of underground structures in high-stress and seismically active regions.

The uniqueness of the current study is that the Incremental Dynamic Analysis (IDA) framework is used to address the issue of seismic behaviour of deep-buried soft rock tunnels that are under high ground stress conditions. Contrary to the majority of the known studies that are based on linear or single-level dynamic analysis, this research is a systematic study of the non-linear seismic response and record-to-record variation of tunnel behavior during incrementally scaled ground motions. Moreover, the paper incorporates IDA-based fragility analysis to determine the likelihood of damage exceedance of the important engineering demand parameters, which is a performance-based analysis that is uncommonly done on tunnels through the large burial depths of the soft rocks. The results provide novel understanding of the processes of degradation of stiffness, amplification of deformation, and susceptibility of underground tunnels in weak rock formations, which is added to the development of performance-based seismic design of underground infrastructure.

2. Incremental dynamic analysis

To evaluate the structural performance under seismic stresses, incremental dynamic analysis (IDA) also known as dynamic pushover, has been developed in several forms [31]. One of the best approaches for examining the impacts of different earthquakes on the behavior of structures is incremental dynamic analysis, which is a commonly used technique for evaluating structural performance under earthquake excitations [32-34]. The collection of ground motion data allows for the direct examination of record-to-record variability in structural response [35]. Incremental dynamic analysis is the foundation of seismic performance evaluation and seismic risk assessment [36]. The widely used structural performance assessment technique is the Incremental Dynamic Analysis (IDA), which involves the assessment of structures with earthquake ground motions at increasingly higher magnitudes [37, 38].

According to D'Ayala et al. (2015) [39], this method effectively calculates the model’s elastic, yielding, nonlinear elastic and global dynamic stability responses. Incremental dynamic analysis is used to forecast the seismic behavior under incrementally scaled ground movements [40, 41].

The most crucial step in conducting an incremental dynamic analysis is to choose an appropriate intensity measure and engineering demand parameter. This analysis represents the relationship between the intensity measure (IM) and the engineering demand parameter (EDP) for the structure. A collection of earthquakes was selected and applied to the structures using the IDA approach [42].

The maximum seismic response of a structure depends strongly on the characteristics of the ground motion used in dynamic analysis. For a given structural system with fixed properties, each earthquake record applied as base excitation can produce a different peak response because of variations in amplitude, frequency content, duration, and phasing. When only a single ground motion is used, the resulting maximum response reflects the behavior under that specific record and cannot be considered representative of the overall seismic demand.

As additional ground motions are considered, a range of response values emerges, revealing the inherent record-to-record variability of seismic demand. With each new input motion, the governing response may increase or decrease, indicating that the critical demand is not known in advance and cannot be reliably captured by a small number of analyses. When a sufficiently large set of ground motions is used, the collection of peak responses forms a stable distribution or envelope, and the identified maximum demand becomes a more reliable estimate of the true extreme response for the chosen hazard level.

According to Soysal and Arici (2014) [43], the intensity measure (IM) is a positive scalar that depends on the strength of the ground motion and increases gradually with the scaling factor. By plotting a judicially selected peak structural response quantity or “engineering demand parameter” (EDP) versus a gradually increasing seismic “intensity measure” (IM), accounting for the uncertainty of the strong ground motion, IDA aims to map the inelastic behavior of yielding structures subjected to strong ground motions [44]. According to Marsed (2017) [31], incremental dynamic analysis considers a structural model as it is affected by one or more ground motion records, each scaled to different degrees of intensity measures.

To carry out an incremental dynamic analysis, the proper values for parameters such as the intensity measure (IM) of ground movements and the damage measure (DM) must be selected.

Intensity Measure (IM) – The most fundamental metrics for the intensity measure are the peak ground acceleration (PGA) and reaction acceleration S_a(Ti, ξ%). As far as possible, a good IM should not be dependent on earthquake data; however certain factors, particularly the PGA, are. According to the growth or reduction of the accelerogram, this number is a function of the initial accelerogram [45]:

where $f$ is a function of a scaled ground motion record, ${\alpha }_1$ is the accelerogram (ground motion time history), and $\lambda$ is the scale factor.

Damage Measure (DM) – Positive numerical values of the damage index indicate that a structure is responding to seismic stresses. In other words, according to Hassanieh et al. (2012) [46], the DM value is a determined number that may reflect a structure's reaction in a dynamics study.

In the elastic region, where it is directly proportional to IM-DM, the IDA curve starts as a straight line [38]. The line begins to curve at larger scaling factors when the seismic loading is sufficient to trigger the nonlinear yielding of the structure. The reaction of a structure to various earthquake intensities is represented by a single IDA curve. Several IDA curves can be displayed on the same graph, each depicting how the structure responds to various seismic events. The different responses of the structure demonstrate the importance of using several IDAs.

Structural response to seismic loading becomes non-linear with increase in intensity of ground motion and this non-linearity depends on the response measure chosen as well as the intensity measure chosen. At low seismic intensity, the structure is largely elastic in behavior, and the correlation between seismic intensity and structural response is monotonic and smooth and predictable. Various response measures within this range have a tendency to show low variations and as the intensity increases, the response also increases proportionately.

Beyond the elastic threshold, inelastic behavior occurs and the intensity response association becomes more complicated. The processes of yielding, loss of stiffness, loss of strength, and redistribution of the internal forces are nonlinear and provide a great level of dispersion to the observed responses. Multiple response values can be met at the same seismic intensity, which is sensitive to the nature of the ground movements and nonlinear nature of the structure. This dispersion grows as the demand becomes more inelastic and it is the characteristic of nonlinear seismic response.

The measures of structural response could display different trends with the increase of intensity. Certain response measures continue to increase monotonically with decreasing slope owing to energy dissipation and yielding, whereas others can be monotonic owing to alteration in dominant response modes, damage localization, or interaction between structural parts. Subsequently, the appearance of a smooth, variability, and explainable relationship between intensity and response depends on the nature of the response measure.

On the same note, measurement of intensity can result in varying degrees of dispersion and efficiency in prediction of structural response. Some of the measures of intensity are more strongly related to particular quantities of response, giving smaller scatter and tighter relationships, others more widely spread, especially in the inelastic range. This tendency shows the need to utilize suitable combinations of the measures of intensity and engineering demand parameters in the context of conducting seismic performance assessment, fragility analysis, or performance-based design because such decisions have a direct impact on the reliability and robustness of the predicted structural demands.

3. Numerical simulation methodology

3.1. Model development

The numerical model creation process is fundamental for determining the true effects of seismic activity on tunnels built within soft rock formations under high ground stresses. The complete numerical model combines the necessary information about geological features with material data, boundary constraints, and seismic force conditions. The study was based on the use of Midas GTS NX in a simulation model to investigate the tunnel response to seismic forces.

The simulation domain contained a semicircular tunnel with a diameter of 10 m and an underground depth of 500 m in the soft rock strata. The choice of the semicircular tunnel section located at a depth of 500 m is justified based on the precedents of the implementation of large-scale underground infrastructure projects in high-stress soft rock environments. An example is the Songshan Lake Tunnel in China, which is a part of the South-to-North Water Diversion Project and has a deep tunnel with a burial depth of up to 400 m or higher in weak surrounding rock, such as mudstone and shale [2]. Similarly, some sections of the Dahuofang Water Conveyance Tunnel in Liaoning Province have depths of more than 500 m and are dominated by soft rock formations with high-stress geometries, preferably circular, as they tend to apply uniform stress and are stable with load excitation [1]. According to geological explorations of these projects, the depth of burial to the rock formation is rated softer, such as weathered sandstone, mudstone, and siltstone which are high in mountainous seismic regions. This supports the realism of the 500 m depth adopted in the current model. Although horseshoe-shaped profiles are typical of transport tunnels, circular profiles are commonly developed in water conveyance tunnels and water mechanical high-pressure systems because they are much more advantageous in stress distribution with high ground pressures. Seismic waves cause rock masses to exhibit low strength and high deformability, along with time-dependent characteristics that affect their response. The numerical model domain requires ample dimensions to reduce boundary effects; thus, it extends five times beyond the tunnel diameter on all sides and reaches twice the depth of the tunnel. Fig. 1 shows the two-dimensional dimensions used in the numerical simulations.

The numerical model assumes that the surrounding soft rock mass behaves as an isotropic continuum, meaning that its mechanical properties are identical in all directions. This assumption is consistent with commonly adopted approaches in preliminary seismic tunnel analyses where large-scale heterogeneity is averaged out for stability and convergence.

Fig. 1Two-dimensional geometry of the numerical model developed in MIDAS GTS NX

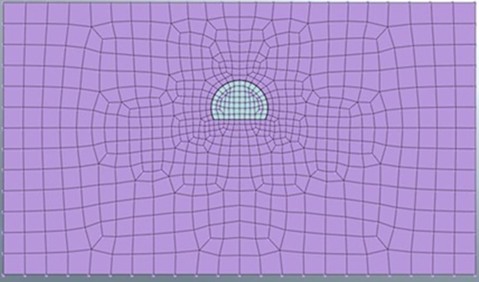
The developed numerical model was bounded by boundary conditions intended to resemble real-life geomechanical constraints and seismic loading patterns.

The side boundaries were set along the sides to represent the restriction of the surrounding rock mass. The bottom layer was fixed in all directions, which were related to a fixed bedrock or bottom layer that was immovable. The nature of the top free surface served as a model to allow free deformation and uplift caused by seismic forces. The loading due to seismic activity was simulated by placing time-history ground motion loads at the base of the model in both the horizontal ($x$) and vertical ($y$) directions. This develops multidirectional ground movements that may occur in real earthquake situations.

The numerical model used the material properties presented in Table 1, including the density, Young’s modulus, Poisson’s ratio, cohesion, friction angle, and damping parameters.

3.2. Seismic input

The seismic performance of buildings exposed to earthquakes of various intensities is assessed using highly accurate and computationally expensive Incremental Dynamic Analysis (IDA) seismic analysis. Incremental dynamic analysis is a crucial method for analyzing the response of buildings to earthquakes. To obtain the global collapse capacity of the structure, an incremental dynamic analysis entails performing a number of nonlinear dynamic studies, during which the intensity of the ground motion exhibited for the assessment is progressively increased. Two separate peak ground accelerations were used for the IDA. A set of three ground movements was used to select the IDA recordings. The MIDAS GTS NX program was used to perform incremental dynamic analysis. The results from the IDA were produced by adding 0.1 g to the nonlinear dynamic analyses. The IDA curves in a 2D graph are represented as the intensity and damage measurements on the vertical and horizontal axes respectively. The definition of earthquake data that will be utilized in numerical model computations is crucial for the incremental dynamic analysis. According to the recommendations of GB50111-06, three earthquake recordings were selected for this analysis.

Table 1Material properties of the soft rock used in the numerical model

Material properties	Value
Young’s modulus	10 GPa
Poisson’s ratio	0.25
Density	2.5 t/m3
Cohesion	10 kPa
Friction angle	30°
Damping ratio	0.05
Note: The soft rock is assumed to behave as a homogeneous and isotropic continuum. Material parameters are representative values commonly adopted for weak rock formations in deep-buried tunnel analyses

Two sets of data were examined for the two potential seismic regions. The analysis was performed on peak ground accelerations of 0.5 and 0.15 g. The selected sets of earthquake recordings are defined in the program SeismoSoft and are displayed in Fig. 2.

Fig. 2Selected earthquake ground motion records for incremental dynamic analysis with peak ground accelerations of 0.5 g and 0.15 g

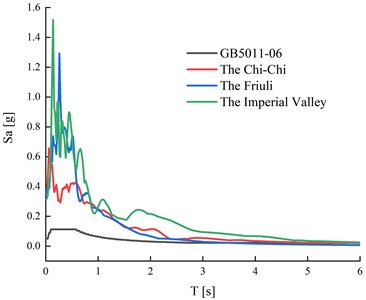
a) 0.5 g

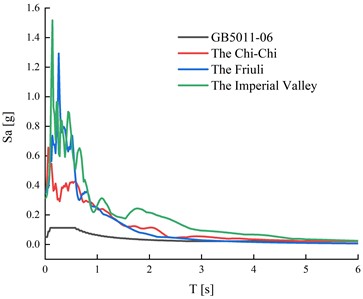
b) 0.15 g

4. Numerical results and discussion

Incremental Dynamic Analysis (IDA) implemented in MIDAS GTS NX is used to evaluate the seismic performance of the soft rock tunnel under peak ground accelerations (PGAs) of 0.15 g and 0.5 g, representing moderate and strong earthquake scenarios, respectively. Three sets of ground motion records (EQ1, EQ2, and EQ3) were applied to the 2D tunnel model to capture record-to-record variability in the seismic response. The key engineering demand parameters (EDPs) discussed in the analysis were the maximum displacement, base shear, and drift ratio; these parameters are suitable for indicating the deformation demand, internal force response, and overall ductility of the structure effectively.

4.1. Displacement response

The time-history response of the two displacement responses of the PGA is illustrated in Fig. 3. All earthquake records also indicated much greater displacements under a more vigorous 0.5 g excitation. For example, for EQ1, the maximum displacement reaches 0.1348 m at 0.5 g, representing an increase of approximately 90 % compared to the response at 0.15 g (0.0709 m). Likewise, EQ2 yielded a maximum displacement of 0.1455 m (66.48 per cent higher than 0.0874 m at 0.15 g), whereas EQ3 yielded 0.1536 m, or approximately 90.81 per cent higher than 0.0805 m at 0.15 g.

This nonlinear increase in displacement indicates that tunnel deformation becomes highly sensitive to PGA once the elastic capacity is exceeded. As shown in Fig. 4, this transition is also confirmed by the fact that the first straight line of the IDA curves corresponds to the elastic region, and beyond that, a curvature is observed as the structure passes to the yielding stage. The nonlinear branch signifies wear-off of the lining and rock interface by progressive stiffness degradation due to plastic deformation. Such findings emphasize the ductile design nature, especially in deep-buried tunnels that are highly prone to seismic excitation in areas where the confinement pressure is high and the stiffness of the soft rock is low.

Fig. 3Time-history displacement responses under peak ground accelerations of 0.5 g and 0.15 g

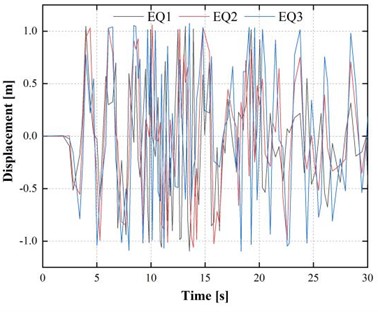
a) 0.5 g

b) 0.15 g

Fig. 4Incremental dynamic analysis (IDA) curves for maximum displacement under peak ground accelerations of 0.5 g and 0.15 g

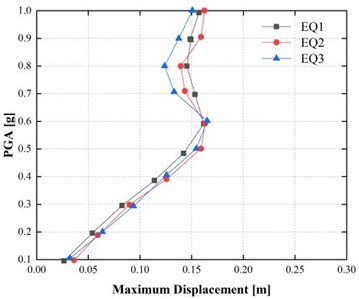
a) 0.5 g

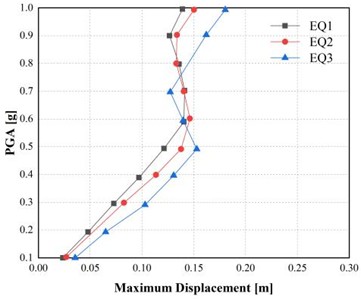
b) 0.15 g

4.2. Base shear response

Fig. 5 shows the variation of maximum base shear under the two PGA levels. The shear force response adhered to a comparable nonlinear escalation rate to that of the displacement. For EQ1, the maximum base shear reached 2.33×10⁶ N, which was 46.54 % higher than the 1.59×10⁶ N corresponding to 0.15 g. For EQ2, the maximum base shear increases to 2.12×10⁶ N at 0.5 g, corresponding to an increase of approximately 46 % compared to the response at 0.15 g, and EQ3, 2.75×10⁶ N, which is 51.10 percent more than the 1.82×10⁶ N at 0.15 g.

This increase in base shear indicates that stronger seismic excitation significantly amplifies internal stresses in the tunnel lining and surrounding rock mass. The results also indicate that local zones of stress concentration occur around the tunnel crown and invert as the PGAs increase, which is consistent with earlier research on the seismic behavior of tunnels [11, 6, 4]. The base shear response under the condition of increasing accelerations increased, which implies the necessity to provide stronger support systems or composite linings that can ensure effective redistribution of the shear demands over the circumference of the tunnel.

Fig. 5Incremental dynamic analysis (IDA) curves for maximum base shear under peak ground accelerations of 0.5 g and 0.15 g

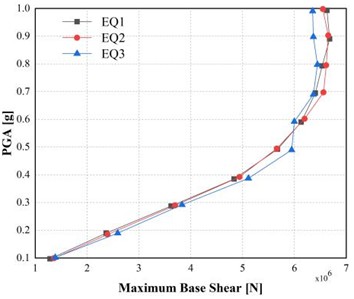
a) 0.5 g

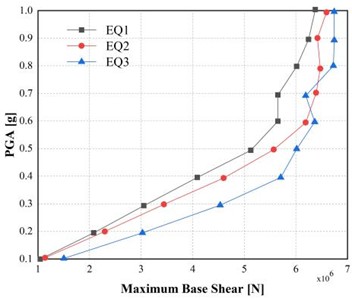
b) 0.15 g

4.3. Drift ratio behavior

The maximum drift ratio, which is a key indicator of the deformation demand relative to the structural height, is presented in Fig. 6. The findings indicate that the drift ratio gradually and consistently increased as the ground acceleration increased. For EQ1, the drift ratio increased from 1.85 % at 0.15 g to 2.04 % at 0.5 g (a 10.27 % increase). For EQ2, it increased by 18.90 % (from 1.27 % to 1.51 %), and for EQ3, it increased by 22.29 % (from 1.36 % to 1.75 %).

Fig. 6Incremental dynamic analysis (IDA) curves for maximum drift ratio under peak ground accelerations of 0.5 g and 0.15 g

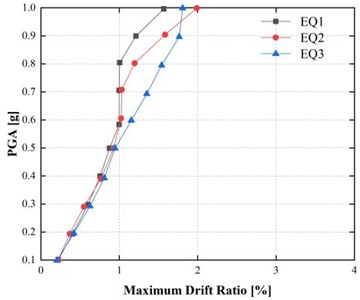
a) 0.5 g

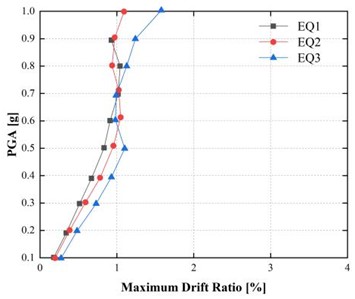
b) 0.15 g

The smaller relative increase in drift ratio compared to displacement and base shear indicates the onset of nonlinear deformation in the tunnel lining. Drift ratios approaching or exceeding 2 % may lead to cracking and joint opening in the tunnel lining particularly in soft rock where tensile strength is limited. This highlights the role of flexible jointing and secondary lining reinforcement of tunnels built in high seismic areas.

4.4. Fragility analysis and damage probability

Fragility curves are developed to quantify the probability of exceeding specific damage states. There are several ways to determine this likelihood, but incremental dynamic analysis is one of the most promising. For each limit state, the cumulative fragility curves were expressed as a lognormal function of the average reaction to earthquakes from the IDA curves. Fragility analysis was performed by processing the IDA results into cumulative probability curves, as shown in Fig. 7. These fragility curves represent the probability of the structure exceeding various damage limit conditions as a measure of the intensity of the ground motion (PGA). In both cases, at 0.15 g and 0.5 g, the fragility curves show a distinct movement in the direction of high probabilities of damage increasing with intensity.

Fig. 7Fragility curves representing damage exceedance probability under peak ground accelerations of 0.5 g and 0.15 g

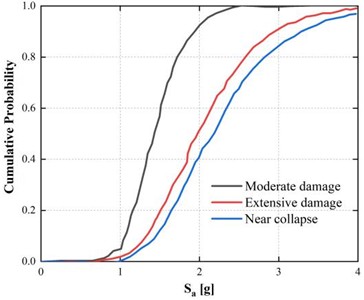
a) 0.5 g

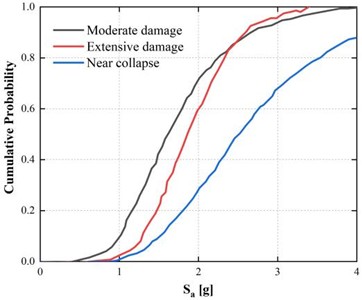
b) 0.15 g

Fig. 7(a) shows that at a PGA of 0.5 g, the fragility curve shifts leftward, indicating earlier yielding and a reduced elastic response range. The steeper gradient of the curve suggests that when yielding commences, the structure rapidly increases the damage states and has limited ductility when subjected to strong excitation. In contrast, in the case of 0.15 g PGA (Fig. 7(b)), the flatter curve implies a wider range of elastic response and a lower likelihood of exceeding the damage limits.

These findings affirm that when the ground stress is high and the rocks are soft, the tunnel lining undergoes a brittle-ductile change as the seismic pressure increases. The obtained fragility functions agree with the results of Liu et al. (2021) [36] and Antoniou et al. (2020) [13] which show that tunnels buried deep underground with low masses of surrounding rocks are likely to experience high rates of stiffness deterioration during repeated seismic cycles.

5. Conclusions

This study presented a performance-based seismic assessment of a deep-buried soft rock tunnel under high ground stress using an Incremental Dynamic Analysis (IDA) framework. By combining nonlinear dynamic analysis with fragility assessment, the proposed approach provides a systematic method for evaluating tunnel response across a wide range of seismic intensities, overcoming the limitations of traditional linear and single-level seismic analyses.

The results revealed pronounced nonlinear behavior of the tunnel as seismic intensity increased, including significant amplification of displacement, base shear, and drift ratio, indicating progressive stiffness degradation and localized yielding of the tunnel lining and surrounding rock mass. The IDA-based fragility analysis demonstrated that strong ground motions substantially increase the probability of exceeding damage limit states, highlighting the vulnerability of deep-buried tunnels excavated in weak rock formations under high in-situ stress.

The main contribution of this study lies in the application of an IDA-based fragility framework to deep-buried soft rock tunnels, providing a vibration-based, probabilistic assessment of seismic performance that captures nonlinear response evolution and record-to-record variability. The findings support the adoption of performance-based seismic design approaches for underground structures in high-stress and seismically active regions.

Future research should extend the present work to three-dimensional modeling, incorporate advanced constitutive models for rock–lining interaction, and investigate the influence of tunnel geometry and support systems to further enhance the seismic resilience of underground infrastructure.