Vibration mechanics of a semi-cylindrical cushion with inertial properties

Akbarli, Reyhan; Garayev, Parviz; Sayfutdinova, Ruzigul; Urolova, Khadicha

doi:10.21595/vp.2025.25749

Vibroengineering Procedia

Browse Procedia

Published: December 22, 2025

Check for updates

Vibration mechanics of a semi-cylindrical cushion with inertial properties

Reyhan Akbarli¹

Parviz Garayev²

Ruzigul Sayfutdinova³

Khadicha Urolova⁴

^{1, 2}Department of Mechanics, Azerbaijan University of Architecture and Construction, Baku, Azerbaijan

^{3, 4}Department of Civil Engineering, Tashkent State Transport University, Tashkent, Uzbekistan

Corresponding Author:

Reyhan Akbarli

Cite the article Download PDF

Downloads 37

Abstract

This study investigates the free and forced vibrations of an inertial semi-cylindrical cushion using the Lamé displacement–based formulation and the Hamilton-Ostrogradsky variational principle. Natural frequencies, vibration modes, and normal displacements were obtained for different boundary conditions. Special attention was given to the influence of inertial and elastic parameters, including density, Young’s modulus, Poisson’s ratio, and foundation inertia. Analytical relations describing the variation of vibration amplitudes and frequencies with respect to geometric and material characteristics were derived. A comparative analysis between the analytical solution and a 3D finite element model developed in ABAQUS demonstrated strong agreement, confirming the accuracy of the proposed formulation. The results provide practical guidelines for optimizing vibration-isolation elements and improve the design of structures exposed to dynamic loads. The study contributes to Sustainable Development Goal 9 by supporting the development of safer and more durable infrastructure components.

1. Introduction

Semi-cylindrical cushions are widely applied in engineering systems exposed to dynamic loading, where accurate prediction of vibration behavior is essential for ensuring structural safety and performance. Previous studies have focused primarily on circular and multilayer plates resting on elastic foundations. Leonenko [1-3] investigated free vibrations of three-layer circular plates on various foundations, providing analytical formulations for frequency prediction. Classical elasticity theory by Novatsky [4] and structural models developed by Amiro and Zarutsky [5] form the theoretical basis for analyzing complex curved bodies. Additional studies have examined shells interacting with elastic and liquid media [6, 7], highlighting the importance of including inertial effects in vibration analysis.

Recent research also emphasizes the role of material innovations and numerical modeling in dynamic systems. Studies on pump components [8], machine elements [9], water-related infrastructure [10, 11], and eco-concretes [12] demonstrate the growing need for reliable vibration models in engineering applications. Composite and fiber-based materials have also been analyzed for acoustic and vibrational properties [13], while surface-treatment studies [14] and deformation modeling in transportation engineering [15] further confirm the relevance of accurate structural vibration analysis across multiple domains.

However, despite these advances, the vibration behavior of inertial semi-cylindrical cushions has not been sufficiently studied. Unlike flat or circular plates, semi-cylindrical elements involve curvature-induced stiffness variation, complex boundary conditions, and significant sensitivity to foundation inertia. These factors necessitate a dedicated analytical approach capable of capturing both geometric and inertial characteristics.

Therefore, this study develops an analytical model for the free vibration of a semi-cylindrical cushion based on the Hamilton-Ostrogradsky variational principle and the Lamé displacement formulation. Material and geometric parameters are explicitly defined, and a numerical algorithm is constructed to compute natural frequencies and displacement fields. The analytical solution is validated through a 3D finite element model developed in ABAQUS to ensure accuracy and reliability.

The cushion material properties are: density $ρ_{s} =$ 7850 kg/m³, Young’s modulus $E_{s} =$ 2.1×10¹¹ Pa, and Poisson’s ratio $ν_{s} =$ 0.30. The geometric parameters are radius $R =$ 0.25 m, thickness $h_{s} =$ 0.012 m, and length $L =$ 0.40-0.80 m. Foundation parameters include stiffness $k_{φ} =$ 1.2×10⁶ N/m³ and inertia $m_{d} =$ 150 kg·s²/m⁴.

2. Problem statement

This study investigates the vibrations of an inertial semi-cylindrical cushion positioned between a bridge span and its support pier (Fig. 1). The aim is to determine the cushion’s dynamic characteristics, assess the effects of its inertial and elastic properties, and establish how vibration amplitudes and frequencies depend on structural parameters.

Fig. 1Inertial semi-cylindrical cushion: p – load applied to the cushion from the bridge side, qr – load applied to the cushion from the support side

To solve the formulated problem, the variational Hamilton-Ostrogradsky principle [4, 5] is applied:

1

δ W = 0,

where, $W = \int_{t^{'}}^{t^{″}} J d t$ is the action functional, and, $t^{'}$ and $t^{''}$ are arbitrarily chosen moments of time:

2

J = V_{k s} - V_{p s} - A_{p} - A_{q},

where, $V_{p s}$ , $V_{k s}$ are the potential and kinetic energies of the semi-cylindrical cushion, respectively; $A_{q}$ is the work of the force acting on the cushion from the bridge side during its vertical displacement, and $A_{p}$ is the work of the force acting from the support side. These quantities are calculated as follows:

3

V_{p s} = ∭ [\frac{λ_{s} + {2 μ}_{s}}{2} (e_{11}^{2} + e_{22}^{2} + e_{33}^{2}) + (λ_{s} + {2 μ}_{s}) (e_{11} e_{22} + e_{22} e_{33} + e_{11} e_{33})],

4

V_{k s} = \frac{ρ_{s}}{2} ∭_{V} {((\frac{\partial s_{x}}{\partial t})}^{2} + {(\frac{\partial s_{θ}}{\partial t})}^{2} + {(\frac{\partial s_{r}}{\partial t})}^{2}) d x d y d r,

5

A_{q} = - \iint_{S} q_{r} {s_{r}|}_{r = 0} d x d y,

6

A_{p} = - \int p (x) {s_{r}|}_{r = R, θ = \frac{π}{2}} d x .

The quantities $s_{x}$ , $s_{θ}$ , $s_{r}$ denote the displacements of the cushion points along the corresponding coordinate directions, and $t$ represents time. The strain components $e_{11}$ , $e_{22}$ , $e_{33}$ are expressed in terms of these displacements $s_{x}$ , $s_{θ}$ , $s_{r}$ as follows:

7

e_{11} = \frac{\partial s_{r}}{\partial r}, e_{22} = R (\frac{\partial s_{θ}}{\partial θ} + s_{r}), e_{33} = \frac{\partial s_{x}}{\partial x} .

It is assumed that the force $q_{r}$ , acting from the support side on the semi-cylindrical cushion during its vertical displacement $s_{r}$ , follows the Winkler-type law:

8

q_{r} = k_{ϑ} s_{r} + m_{d} \frac{\partial^{2} s_{r}}{\partial t^{2}},

where $k_{ϑ}$ is the stiffness coefficient, and $m_{d}$ is the specific weight of the support material. The load from the bridge side acting on the cushion is defined by the function:

9

P (x) = p_{0} c o s \frac{n π}{2} s i n k x s i n ω t .

The displacements of the inertial semi-cylindrical cushion $s_{x}$ , $s_{θ}$ , $s_{r}$ are described by the Lamé equations in vector form [6, 7]:

10

a_{l}^{2} g r a d d i v \vec{u} - a_{t}^{2} r o t r o t \vec{u} + ρ_{s} \frac{\partial^{2} \vec{u}}{\partial t^{2}} = 0,

where $a_{t} = \sqrt{\frac{λ_{s} + 2 μ_{s}}{ρ_{s}}}$ , $a_{e} = \sqrt{\frac{μ_{s}}{ρ_{s}}}$ are the longitudinal and transverse wave propagation velocities, $ρ_{s}$ is the density, $λ_{s}$ and $μ_{s}$ are the Lamé coefficients.

3. Numerical method

The analytical expressions obtained from the assumed displacement functions were evaluated numerically using MATLAB. All integrals appearing in the kinetic and strain energy formulations were computed using standard Gaussian quadrature. Substituting these expressions into the Hamilton-Ostrogradsky functional leads to a system of algebraic equations that can be written in matrix form as $A (ω) C = B$ , where $A (ω)$ depends on the vibration frequency and the material and geometric parameters of the cushion.

The natural frequencies were determined by solving the characteristic equation $d e t A (ω) =$ 0.

The nonlinear equation was solved using the Newton–Raphson method, ensuring rapid convergence. After obtaining each resonant frequency, displacement coefficients 𝐶 were calculated using Cramer’s rule and substituted into the assumed displacement field to determine mode shapes. Stability and convergence were verified by refining the integration scheme and testing multiple mesh densities, confirming the reliability of the algorithm.

4. Solution

The displacements of the inertial semi-cylindrical cushion $s_{x}$ , $s_{θ}$ , $s_{r}$ are given in the following form [6]:

11

s_{x} = [{\tilde{A}}_{s} k I_{n} (γ_{e} r) - \frac{{\tilde{C}}_{s} γ_{t}^{2}}{μ_{t}} I_{n} (γ_{t} r)] \cos n θ \cos k x \sin ω t,

s_{θ} = [- \frac{{\tilde{A}}_{s} n}{r} I_{n} (γ_{e} r) - \frac{{\tilde{C}}_{s} n k}{r μ_{t}} I_{n} (γ_{t} r) - \frac{{\tilde{B}}_{s}}{n} \frac{\partial I_{n} (γ_{t} r)}{\partial r}] \sin n θ \sin k x \sin ω t,

s_{r} = [{\tilde{A}}_{s} \frac{\partial I_{n} (γ_{e} r)}{\partial r} - \frac{{\tilde{C}}_{s} k}{μ_{t}} \frac{\partial I_{n} (γ_{t} r)}{\partial r} + \frac{{\tilde{B}}_{s} n}{r} I_{n} (γ_{t} r)] \cos n θ \sin k x \sin ω t,

where ${\tilde{A}}_{s}$ , ${\tilde{C}}_{s}$ , ${\tilde{B}}_{s}$ are unknown constant coefficients, and $k$ , $n$ , $γ_{e}$ , $γ_{t}$ – are the wave numbers and $γ_{e}^{2} = k^{2} - μ_{e}^{2}$ , $γ_{t}^{2} = k^{2} - μ_{t}^{2}$ .

By substituting Eq. (10) into Eqs. (3-6), the expressions for the potential and kinetic energies of the cushion are obtained:

12

V_{p s} = \frac{π l (λ_{s} + {2 μ}_{s})}{16} \{{\tilde{A}}_{s}^{2} \int_{0}^{R} [γ_{l}^{4} {I_{n}^{''}}^{2} (γ_{l} r) + k^{4} I_{n}^{2} (γ_{l} r) - 2 k^{2} γ_{l}^{2} I_{n} (γ_{l} r) I_{n}^{''} (γ_{l} r)

+ β_{1} (R^{2} + 2 γ_{l}^{2} R) I_{n}^{''} (γ_{l} r) - 2 k^{2} R I_{n} (γ_{l} r)] d r + {\tilde{B}}_{s}^{2} \int_{0}^{R} (β_{2}^{2} + R^{2} β_{3} + β_{2} β_{3}) d r

{+ \tilde{C}}_{s}^{2} \int_{0}^{R} [\frac{k^{2} γ_{t}^{4}}{μ_{t}^{2}} {I_{n}^{''}}^{2} (γ_{t} r) + \frac{k^{2} γ_{t}^{4}}{μ_{t}^{2}} I_{n}^{2} (γ_{t} r) - \frac{k^{2} γ_{t}^{4}}{μ_{t}^{2}} I_{n} (γ_{t} r) I_{n}^{''} (γ_{t} r) + β_{4} \frac{k γ_{t}^{2}}{μ_{t}}

\times R I_{n} (γ_{t} r) - I_{n}^{''} (γ_{t} r)] d r + {\tilde{A}}_{s} {\tilde{C}}_{s} \int_{0}^{R} [\frac{- 2 k γ_{l}^{2} γ_{t}^{2}}{μ_{t}} I_{n}^{''} (γ_{l} r) I_{n}^{''} (γ_{t} r) - \frac{2 γ_{t}^{2} k^{3}}{μ_{t}} I_{n} (γ_{l} r)

\times I_{n} (γ_{t} r) + \frac{k γ_{l}^{2} γ_{t}^{2}}{μ_{t}} I_{n} (γ_{t} r) I_{n}^{''} (γ_{l} r) + \frac{γ_{t}^{2} k^{3}}{μ_{t}} I_{n} (γ_{l} r) I_{n}^{''} (γ_{t} r) + 2 β_{4} β_{5}

+ β_{4} (γ_{l}^{2} {R I_{n}^{''} (γ_{l} r) - k^{2} R I}_{n} (γ_{l} r)) + β_{5} \frac{k γ_{t}^{2}}{μ_{t}} I_{n} (γ_{l} r) - R I_{n}^{''} (γ_{t} r)] d r

+ {\tilde{A}}_{s} {\tilde{B}}_{s} \int_{0}^{R} [2 γ_{l}^{2} β_{2} I_{n}^{''} (γ_{t} r) + {2 R}^{2} β_{1} β_{3} + γ_{l}^{2} β_{3} I_{n}^{''} (γ_{l} r) + β_{1} β_{2} - k^{2} β_{2} I_{n} (γ_{l} r)

- k^{2} {R β}_{3} I_{n} (γ_{l} r)] d r + {\tilde{B}}_{s} {\tilde{C}}_{s} \int_{0}^{R} [- \frac{2 k γ_{t}^{2} β_{2}}{μ_{t}} I_{n}^{''} (γ_{t} r) + 2 R^{2} β_{3} β_{4} - \frac{2 k γ_{t}^{2} {R β}_{3}}{μ_{t}}

\times I_{n}^{''} (γ_{t} r) + \frac{k γ_{t}^{2} β_{2}}{μ_{t}} I_{n} (γ_{t} r) + \frac{k γ_{t}^{2} {R β}_{3}}{μ_{t}} I_{n} (γ_{t} r) + R β_{2} β_{4}] d r\} {s i n}^{2} ω t,

β_{1} (r) = - \frac{n^{2}}{r} I_{n} (γ_{l} r) + γ_{l} I_{n}^{'} (γ_{l} r), β_{2} (r) = \frac{n γ_{t}}{r} I_{n}^{'} (γ_{t} r) - \frac{n}{r^{2}} I_{n} (γ_{t} r),

β_{3} (r) = - γ_{t} I_{n}^{'} (γ_{t} r) + \frac{n}{r} I_{n} (γ_{t} r), β_{4} (r) = - \frac{k}{μ_{t}} (\frac{n^{2}}{r} I_{n} (γ_{t} r) - γ_{t} I_{n}^{'} (γ_{t} r)),

β_{5} (r) = - \frac{n^{2}}{r} I_{n} (γ_{l} r) + γ_{l} I_{n}^{'} (γ_{l} r),

V_{k s} = \frac{π l ω^{2} ρ_{s}}{8} \{{\tilde{A}}_{s}^{2} \int_{0}^{R} [k^{2} I_{n}^{2} (γ_{l} r) + \frac{n^{2}}{r^{2}} I_{n}^{2} (γ_{l} r) + γ_{l}^{2} {I_{n}^{'}}^{2} (γ_{l} r)] d r

{+ \tilde{B}}_{s}^{2} \int_{0}^{R} [\frac{γ_{t}^{2}}{n^{2}} {I_{n}^{'}}^{2} (γ_{l} r) + \frac{n^{2}}{r^{2}} I_{n}^{2} (γ_{t} r)] d r {+ \tilde{C}}_{s}^{2} \int_{0}^{R} [\frac{γ_{t}^{4}}{μ_{t}^{2}} I_{n} (γ_{t} r) + \frac{n^{2} k^{2}}{r^{2} μ_{t}^{2}} I_{n}^{2} (γ_{t} r)

+ \frac{{k^{2} γ}_{t}^{2}}{μ_{t}^{2}} {I_{n}^{'}}^{2} (γ_{t} r)] d r + {\tilde{A}}_{s} {\tilde{C}}_{s} \int_{0}^{R} [- 2 k γ_{t}^{2} I_{n} (γ_{l} r) I_{n} (γ_{t} r) + \frac{{2 n}^{2} k}{r^{2} μ_{t}} I_{n} (γ_{l} r) I_{n} (γ_{t} r)

- \frac{2 k γ_{l} γ_{t}}{μ_{t}} I_{n}^{'} (γ_{l} r) I_{n}^{'} (γ_{t} r)] d r + {\tilde{A}}_{s} {\tilde{B}}_{s} \int_{0}^{R} [\frac{2 γ_{t}}{r} I_{n} (γ_{l} r) I_{n}^{'} (γ_{t} r)

+ \frac{2 n γ_{l}}{r} I_{n} (γ_{t} r) I_{n}^{'} (γ_{l} r)] d r + {\tilde{B}}_{s} {\tilde{C}}_{s} \int_{0}^{R} [\frac{2 k γ_{t}}{μ_{t}} {I_{n} (γ_{t} r) I}_{n}^{'} (γ_{t} r)

- \frac{2 n k γ_{t}}{r μ_{t}} {I_{n} (γ_{t} r) I}_{n}^{'} (γ_{t} r)] d r\} {s i n}^{2} ω t,

A_{q} = - \frac{π l R}{4} [A_{s}^{2} \int_{0}^{R} γ_{l}^{2} {I_{n}^{'}}^{2} (γ_{l} r) d r {+ \tilde{C}}_{s}^{2} \frac{k^{2} γ_{t}^{2}}{μ_{t}^{2}} \int_{0}^{R} {I_{n}^{'}}^{2} (γ_{t} r) d r {+ \tilde{B}}_{s}^{2} n^{2} \int_{0}^{R} \frac{I_{n}^{2} (γ_{t} r)}{r^{2}} d r

- {\tilde{A}}_{s} {\tilde{C}}_{s} \frac{2 k γ_{l} γ_{t}}{μ_{t}} \int_{0}^{R} I_{n}^{'} (γ_{l} r) I_{n}^{'} (γ_{t} r) d r + {\tilde{A}}_{s} {\tilde{B}}_{s} ∙ 2 γ_{l} n \int_{0}^{R} \frac{I_{n} (γ_{t} r) I_{n}^{'} (γ_{l} r)}{r} d r

- {\tilde{B}}_{s} {\tilde{C}}_{s} \frac{2 n k γ_{t}}{μ_{t}} \int_{0}^{R} \frac{{I_{n} (γ_{t} r) I}_{n}^{'} (γ_{t} r)}{r} d r] (k_{ϑ} - ω^{2} m_{d}) {s i n}^{2} ω t,

A_{p} = - \frac{p_{0} l}{2} [{\tilde{A}}_{s} \frac{\partial I_{n} (γ_{e} R)}{\partial r} - \frac{{\tilde{C}}_{s} k}{μ_{t}} \frac{\partial I_{n} (γ_{t} R)}{\partial r} + \frac{{\tilde{B}}_{s} n}{R} I_{n} (γ_{t} R)] \sin^{2} ω t .

By substituting all expressions from Eq. (11) into Eq. (2) for the $J$ and taking $t^{'} = 0$ , $t^{''} = π / ω$ , and applying the Hamilton-Ostrogradsky variational principle Eq. (1), the following expression is obtained:

13

W = \{\frac{π l ω^{2} ρ_{s}}{8} \{{\tilde{A}}_{s}^{2} \int_{0}^{R} [k^{2} I_{n}^{2} (γ_{l} r) + \frac{n^{2}}{r^{2}} I_{n}^{2} (γ_{l} r) + γ_{l}^{2} {I_{n}^{'}}^{2} (γ_{l} r)] d r

{+ \tilde{B}}_{s}^{2} \int_{0}^{R} [\frac{γ_{t}^{2}}{n^{2}} {I_{n}^{'}}^{2} (γ_{l} r) + \frac{n^{2}}{r^{2}} I_{n}^{2} (γ_{t} r)] d r {+ \tilde{C}}_{s}^{2} \int_{0}^{R} [\frac{γ_{t}^{4}}{μ_{t}^{2}} I_{n} (γ_{t} r) + \frac{n^{2} k^{2}}{r^{2} μ_{t}^{2}} I_{n}^{2} (γ_{t} r)

+ \frac{{k^{2} γ}_{t}^{2}}{μ_{t}^{2}} {I_{n}^{'}}^{2} (γ_{t} r)] d r + {\tilde{A}}_{s} {\tilde{C}}_{s} \int_{0}^{R} [- 2 k γ_{t}^{2} I_{n} (γ_{l} r) I_{n} (γ_{t} r) + \frac{{2 n}^{2} k}{r^{2} μ_{t}} I_{n} (γ_{l} r) I_{n} (γ_{t} r)

- \frac{2 k γ_{l} γ_{t}}{μ_{t}} I_{n}^{'} (γ_{l} r) I_{n}^{'} (γ_{t} r)] d r + {\tilde{A}}_{s} {\tilde{B}}_{s} \int_{0}^{R} [\frac{2 γ_{t}}{r} I_{n} (γ_{l} r) I_{n}^{'} (γ_{t} r)

+ \frac{2 n γ_{l}}{r} I_{n} (γ_{t} r) I_{n}^{'} (γ_{l} r)] d r + {\tilde{B}}_{s} {\tilde{C}}_{s} \int_{0}^{R} [\frac{2 k γ_{t}}{μ_{t}} {I_{n} (γ_{t} r) I}_{n}^{'} (γ_{t} r)

- \frac{2 n k γ_{t}}{r μ_{t}} {I_{n} (γ_{t} r) I}_{n}^{'} (γ_{t} r)] d r - \frac{π l (λ_{s} + {2 μ}_{s})}{16} \{{\tilde{A}}_{s}^{2} \int_{0}^{R} [γ_{l}^{4} {I_{n}^{''}}^{2} (γ_{l} r) + k^{4} I_{n}^{2} (γ_{l} r)

- 2 k^{2} γ_{l}^{2} I_{n} (γ_{l} r) I_{n}^{''} (γ_{l} r) + β_{1} (R^{2} + 2 γ_{l}^{2} R) I_{n}^{''} (γ_{l} r) - 2 k^{2} R I_{n} (γ_{l} r)] d r

+ {\tilde{B}}_{s}^{2} \int_{0}^{R} (β_{2}^{2} + R^{2} β_{3} + β_{2} β_{3}) d r {+ \tilde{C}}_{s}^{2} \int_{0}^{R} [\frac{k^{2} γ_{t}^{4}}{μ_{t}^{2}} {I_{n}^{''}}^{2} (γ_{t} r) + \frac{k^{2} γ_{t}^{4}}{μ_{t}^{2}} I_{n}^{2} (γ_{t} r)

- \frac{k^{2} γ_{t}^{4}}{μ_{t}^{2}} I_{n} (γ_{t} r) I_{n}^{''} (γ_{t} r) + β_{4} \frac{k γ_{t}^{2}}{μ_{t}} \times R I_{n} (γ_{t} r) - I_{n}^{''} (γ_{t} r)] d r

+ {\tilde{A}}_{s} {\tilde{C}}_{s} \int_{0}^{R} [\frac{- 2 k γ_{l}^{2} γ_{t}^{2}}{μ_{t}} I_{n}^{''} (γ_{l} r) I_{n}^{''} (γ_{t} r) - \frac{2 γ_{t}^{2} k^{3}}{μ_{t}} I_{n} (γ_{l} r) \times I_{n} (γ_{t} r)

+ \frac{k γ_{l}^{2} γ_{t}^{2}}{μ_{t}} I_{n} (γ_{t} r) I_{n}^{''} (γ_{l} r) + \frac{γ_{t}^{2} k^{3}}{μ_{t}} I_{n} (γ_{l} r) I_{n}^{''} (γ_{t} r) + 2 β_{4} β_{5}

+ β_{4} (γ_{l}^{2} {R I_{n}^{''} (γ_{l} r) - k^{2} R I}_{n} (γ_{l} r)) + β_{5} \frac{k γ_{t}^{2}}{μ_{t}} I_{n} (γ_{l} r) - R I_{n}^{''} (γ_{t} r)] d r

+ {\tilde{A}}_{s} {\tilde{B}}_{s} \int_{0}^{R} [2 γ_{l}^{2} β_{2} I_{n}^{''} (γ_{t} r) + {2 R}^{2} β_{1} β_{3} + γ_{l}^{2} β_{3} I_{n}^{''} (γ_{l} r) + β_{1} β_{2} - k^{2} β_{2} I_{n} (γ_{l} r)

- k^{2} {R β}_{3} I_{n} (γ_{l} r)] d r + {\tilde{B}}_{s} {\tilde{C}}_{s} \int_{0}^{R} [- \frac{2 k γ_{t}^{2} β_{2}}{μ_{t}} I_{n}^{''} (γ_{t} r) + 2 R^{2} β_{3} β_{4} - \frac{2 k γ_{t}^{2} {R β}_{3}}{μ_{t}}

\times I_{n}^{''} (γ_{t} r) + \frac{k γ_{t}^{2} β_{2}}{μ_{t}} I_{n} (γ_{t} r) + \frac{k γ_{t}^{2} {R β}_{3}}{μ_{t}} I_{n} (γ_{t} r) + R β_{2} β_{4}] d r

+ \frac{π l R}{4} [A_{s}^{2} \int_{0}^{R} γ_{l}^{2} {I_{n}^{'}}^{2} (γ_{l} r) d r {+ \tilde{C}}_{s}^{2} \frac{k^{2} γ_{t}^{2}}{μ_{t}^{2}} \int_{0}^{R} {I_{n}^{'}}^{2} (γ_{t} r) d r {+ \tilde{B}}_{s}^{2} n^{2} \int_{0}^{R} \frac{I_{n}^{2} (γ_{t} r)}{r^{2}} d r

- {\tilde{A}}_{s} {\tilde{C}}_{s} \frac{2 k γ_{l} γ_{t}}{μ_{t}} \int_{0}^{R} I_{n}^{'} (γ_{l} r) I_{n}^{'} (γ_{t} r) d r + {\tilde{A}}_{s} {\tilde{B}}_{s} ∙ 2 γ_{l} n \int_{0}^{R} \frac{I_{n} (γ_{t} r) I_{n}^{'} (γ_{l} r)}{r} d r

- {\tilde{B}}_{s} {\tilde{C}}_{s} \frac{2 n k γ_{t}}{μ_{t}} \int_{0}^{R} \frac{{I_{n} (γ_{t} r) I}_{n}^{'} (γ_{t} r)}{r} d r] (k_{ϑ} - ω^{2} m_{d})

+ \frac{p_{0} l}{2} [{\tilde{A}}_{s} \frac{\partial I_{n} (γ_{e} R)}{\partial r} - \frac{{\tilde{C}}_{s} k}{μ_{t}} \frac{\partial I_{n} (γ_{t} R)}{\partial r} + \frac{{\tilde{B}}_{s} n}{R} I_{n} (γ_{t} R)]\} ∙ \frac{π}{2 ω} .

From Eq. (12) for $W$ , it follows that the functional represents a quadratic form with respect to the constants ${\tilde{A}}_{s}$ , ${\tilde{B}}_{s}$ , ${\tilde{C}}_{s}$ . By varying the functional with respect to these unknowns ${\tilde{A}}_{s}$ , ${\tilde{B}}_{s}$ , ${\tilde{C}}_{s}$ , a system of non-homogeneous algebraic equations is obtained:

\frac{\partial W}{\partial {\tilde{A}}_{s}} = φ_{1}, \frac{\partial W}{\partial {\tilde{B}}_{s}} = φ_{2}, \frac{\partial W}{\partial {\tilde{C}}_{s}} = φ_{3} .

In expanded form, the system of equations is as follows:

14

φ_{11} A_{s} + φ_{12} B_{s} + φ_{13} C_{s} = - \frac{l p_{0}}{2}, φ_{21} A_{s} + φ_{22} B_{s} + φ_{23} C_{s} = - \frac{l p_{0}}{2},

φ_{31} A_{s} + φ_{32} B_{s} + φ_{33} C_{s} = - \frac{l p_{0}}{2} \frac{n I_{n} (γ_{t} R)}{R},

where the coefficients $φ_{i j}$ ( $i$ , $j =$ 1, 2, 3) are obtained from the variational functional $W$ after variation as the coefficients of the constants ${\tilde{A}}_{s}$ , ${\tilde{B}}_{s}$ , ${\tilde{C}}_{s}$ . Using Cramer’s rule, these constants are determined as follows:

15

{\tilde{A}}_{s} = \frac{∆_{1}}{∆}, {\tilde{B}}_{s} = \frac{∆_{2}}{∆}, {\tilde{C}}_{s} = \frac{∆_{3}}{∆},

where, $∆$ is the main determinant of the system, and $∆_{i}$ ( $i =$ 1, 2, 3) are the auxiliary determinants of the Eq. (14). By substituting the values of ${\tilde{A}}_{s}$ , ${\tilde{B}}_{s}$ , ${\tilde{C}}_{s}$ from Eq. (15) into Eq. (10) for $s_{r}$ , the final formula for the cushion displacement is obtained:

s_{r} = [{\tilde{A}}_{s} \frac{\partial I_{n} (γ_{e} R)}{\partial r} - \frac{{\tilde{C}}_{s} k}{μ_{t}} \frac{\partial I_{n} (γ_{t} R)}{\partial r} + \frac{{\tilde{B}}_{s} n}{R} I_{n} (γ_{t} R)] \cos \frac{n π}{2} \sin k x \sin ω t .

The resonance frequencies of the cushion are determined from the condition $∆ = 0$ . The roots of the equation $∆ = 0$ are found numerically. For the calculations, the following parameters characterizing the material of the semi-cylindrical cushion are adopted: $k_{ϑ} =$ 50 MPa/m, $m_{d} =$ 1000 MPa/m.

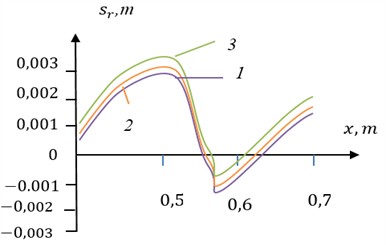
The dependence of the natural frequencies of the semi-cylindrical cushion on its length is shown in Fig. 2. The normal displacements of surface points of the cushion as functions of the coordinates for different values of the foundation’s specific weight are shown in Fig. 3. In all graphs: curve 1 corresponds to $m_{d} =$ 1000 MPa/m, curve 2 to $m_{d} =$ 1500 MPa/m, and curve 3 to $m_{d} =$ 2000 MPa/m.

A decrease in frequency is observed with increasing length due to reduced stiffness-to-mass ratio.

Fig. 2Fundamental natural frequency of the semi-cylindrical cushion as a function of its length

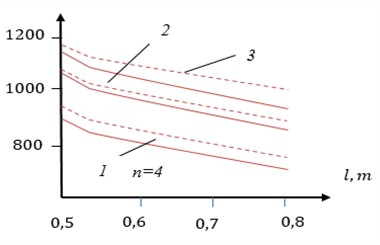
Fig. 3Vertical deflection profile of the semi-cylindrical cushion for different values of foundation inertia md. Curve 1 – low inertia; Curve 2 – medium; Curve 3 – high inertia

5. Model validation

A 3D FEM model of the semi-cylindrical cushion was created in ABAQUS to verify the analytical model, replicating all boundary conditions and material properties. Using 8-node C3D8 elements and mesh convergence, natural frequencies were computed via the Lanczos method. Comparison with analytical results showed differences below 2.8 % for the first three modes, confirming the validity of the displacement functions and variational equations. This demonstrates the model’s reliability for parameter studies, optimization, and vibration isolation design.

6. Discussion

Analytical and FEM results reveal the dynamic behavior of the semi-cylindrical cushion, influenced by geometry, material properties, and foundation inertia. Longer cushions lower natural frequencies, while heavier foundations increase vertical displacements. Higher stiffness raises frequencies, whereas higher density lowers them. Close agreement between analytical and FEM models (< 3 % deviation) confirms the formulation’s validity, emphasizing the need to optimize geometry, material, and foundation parameters for effective bridge vibration isolation.

7. Conclusions

1) Increasing the length of the semi-cylindrical cushion leads to a decrease in its natural vibration frequencies.

2) An increase in the specific weight of the support results in higher natural vibration frequencies.

3) An increase in the specific weight of the foundation causes greater deflection of the cushion.

4) The inertial properties of the semi-cylindrical cushion lead to a reduction in its natural frequencies.

References

L. D. Leonenko, “Free vibrations of a three-layer circular plate on an inertial foundation under thermal effects,” Izvestiya of F. Skorina Gomel State University, Natural Sciences, No. 6, pp. 174–179, 2019.

Search CrossRef
D. V. Leonenko, “Free vibrations of three-layer circular plates on an elastic foundation,” Ecological Bulletin of Scientific Centers of Black Sea Economic Cooperation, No. 3, pp. 42–47, 2008.

Search CrossRef
D. V. Leonenko, “Free vibrations of three-layer circular plates on a Pasternak elastic foundation,” Ecological Bulletin of Scientific Centers of Black Sea Economic Cooperation, No. 1, pp. 59–63, 2014.

Search CrossRef
V. Novatsky, Theory of Elasticity. Moscow: Mir Publishers, 1975.

Search CrossRef
I. Y. Amiro and V. A. Zarutsky, Theory of Ribbed Shells: Methods for Shell Calculation. Kyiv: Naukova Dumka, 1980.

Search CrossRef
F. S. Latifov, Vibrations of Shells with Elastic and Liquid Medium. Baku, 1999.

Search CrossRef
Y. A. Amanzade, Theory of Elasticity. Moscow: Higher School Publishing, 1976.

Search CrossRef
O. Glovatskii et al., “Modernization of submersible pump designs for sustainable irrigation: A bibliometric and experimental contribution to Sustainable Development Goals (SDGs),” Indonesian Journal of Science and Technology, Vol. 10, No. 3, pp. 427–438, Jun. 2025, https://doi.org/10.17509/ijost.v10i3.85476

Publisher
A. Mamahonov, I. Khikmatillaev, and D. Kholbaev, “Automatic determination and control of working body loads of technological machines,” in International Conference on Physical Research and Engineering Technology Problems, Vol. 3304, p. 030083, Jan. 2025, https://doi.org/10.1063/5.0269315

Publisher
D. Hammoumi, H. S. Al-Aizari, Z. Alkhawlani, S. Chakiri, and Z. Bejjaji, “water quality assessment using the water quality index, and geographic information systems in Nador Canal, Morocco,” Journal of Environmental and Earth Sciences, Vol. 6, No. 2, pp. 1–16, May 2024, https://doi.org/10.30564/jees.v6i2.6310

Publisher
C. Yerli and U. Sahin, “Reducing gray, blue, green, and total water footprint in wastewater irrigated silage maize in zero tillage,” Journal of Water and Climate Change, Vol. 15, No. 12, pp. 5778–5792, Dec. 2024, https://doi.org/10.2166/wcc.2024.278

Publisher
H. Bentegri et al., “Assessment of compressive strength of eco-concrete reinforced using machine learning tools,” Scientific Reports, Vol. 15, No. 1, Feb. 2025, https://doi.org/10.1038/s41598-025-89530-y

Publisher
V. Sekar, S. Palaniyappan, S. Y. Eh Noum, A. Putra, S. Sivanesan, and D. D. Chin Vui Sheng, “Acoustic absorbers made of wood fiber composites developed by compression molding and additive manufacturing,” Wood Research, Vol. 68, No. 1, pp. 68–82, Feb. 2023, https://doi.org/10.37763/wr.1336-4561/68.1.6882

Publisher
Z. Aringozhina, B. Rakhadilov, D. Yeskermessov, Y. Tabiyeva, and W. Ahmed, “Study of the Influence of Electrolytic-Plasma Treatment on the Tribological Properties of High-Speed Steel,” Advances in Chemical and Materials Engineering, pp. 22–82, Sep. 2023, https://doi.org/10.4018/978-1-6684-6830-2.ch002

Publisher
Y. Y. Rustamov and G. N. Akhundov, “Study of deformations caused by passenger and freight trains in the soil bed during movement,” Scientific Works, 2023.

Search CrossRef

About this article

Received

October 27, 2025

Accepted

November 18, 2025

Published

December 22, 2025

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2025.25749

Keywords

dynamic behavior

inertial properties

natural frequencies

semi-cylindrical cushion

vibrations

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

R. Akbarli, P. Garayev, R. Sayfutdinova, and K. Urolova, “Vibration mechanics of a semi-cylindrical cushion with inertial properties,” Vibroengineering Procedia, Vol. 60, pp. 16–23, Dec. 2025, https://doi.org/10.21595/vp.2025.25749

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2025.25749
UR  - https://doi.org/10.21595/vp.2025.25749
TI  - Vibration mechanics of a semi-cylindrical cushion with inertial properties
T2  - Vibroengineering Procedia
AU  - Akbarli, Reyhan
AU  - Garayev, Parviz
AU  - Sayfutdinova, Ruzigul
AU  - Urolova, Khadicha
PY  - 2025
DA  - 2025/12/22
PB  - Extrica
SP  - 16-23
VL  - 60
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Akbarli_2025, title={Vibration mechanics of a semi-cylindrical cushion with inertial properties}, volume={60}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2025.25749}, DOI={10.21595/vp.2025.25749}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Akbarli, Reyhan and Garayev, Parviz and Sayfutdinova, Ruzigul and Urolova, Khadicha}, year={2025}, month=dec, pages={16–23} }

Copy Bibtex

Copied to clipboard!

[1]R. Akbarli, P. Garayev, R. Sayfutdinova, and K. Urolova, “Vibration mechanics of a semi-cylindrical cushion with inertial properties,” Vibroengineering Procedia, vol. 60, pp. 16–23, Dec. 2025, doi: 10.21595/vp.2025.25749.

Copy IEEE

Copied to clipboard!

Akbarli, Reyhan, Parviz Garayev, Ruzigul Sayfutdinova, and Khadicha Urolova. “Vibration Mechanics of a Semi-Cylindrical Cushion with Inertial Properties.” Vibroengineering Procedia 60 (December 22, 2025): 16–23. https://doi.org/10.21595/vp.2025.25749.

Copy Chicago

Copied to clipboard!

Vibration mechanics of a semi-cylindrical cushion with inertial properties

Abstract

1. Introduction

2. Problem statement

3. Numerical method

4. Solution

5. Model validation

6. Discussion

7. Conclusions

References

About this article

Related Articles