Strain mode based damage assessment for plate like structures

2.1. Dynamic equation and modal analysis

The equation of motion for a finite element model can be written as:

where $\left[M\right]$, $\left[C\right]$ and $\left[K\right]$ are the mass, damping and stiffness matrixes, respectively, $\left\{f\right\}$ is the external excitation, and $\left\{\ddot{\delta }\right\}$, $\left\{\dot{\delta }\right\}$ and $\left\{\delta \right\}$ are the acceleration, velocity and displacement responses of structures.

Under the assumption of proportional damping, this physical system can be transferred into modal domain and its solution can be expressed as:

where $\left[\mathrm{\Phi }\right]$ is the displacement modal matrix satisfying:

in which, ${\omega }_i$ and ${\zeta }_i$ are natural frequency and damping ratio of $i$th vibration mode, respectively. $\left\{Q\right\}$ is the modal coordinate response, and its $i$th component $q_i$ is governed by:

where $\left\{{\varphi }_i\right\}$ is the $i$th mode shape vector.

2.2. Derivation of modal strain

Notice the following relationship between strains and displacements:

where $u$ and $v$ are displacements along x and y axes respectively. The transformation equation of strain mode shapes from displacement mode shapes can be expressed as [7]:

where $\left[B\right]$ is the transfer matrix in dependence on the discrete finite element model and the adoptive difference scheme, and $\left[{\mathrm{\Phi }}^{\epsilon }\right]$ presents the strain mode shape matrix.

2.3. Increment of modal strain

A damage occurring in the structure may leads to a variation of structural dynamic parameters as stiffness matrix, natural frequency, modal strain, modal displacement, modal curvature, etc. Suppose stiffness matrix, square of natural frequency and modal displacement matrix of the damaged structure are $K_d$, ${\lambda }_d={\omega }_d^2$ and ${\mathrm{\Phi }}_d$, respectively. Then the incremental forms of stiffness matrix, square of natural frequency and modal displacement matrix can be written as:

The above dynamic parameters must satisfy the eigenvalues equations as follows:

Substituting equation (4) into (5) yields:

which, by neglecting the higher order terms, leads to:

Thus:

In terms of the invariance of transfer matrix B in equation (6) with structural damage, the incremental form of modal strain can be derived as:

If the changes of structural frequency can be further neglected, the increment of strain mode shapes caused only by $\mathrm{\Delta }K$ is:

Therefore $\mathrm{\Delta }K$ is the only variable at the right-hand side, which means that $\mathrm{\Delta }\mathrm{\Phi }$ and $\mathrm{\Delta }K$ is of a linear relationship approximately when $\mathrm{\Delta }K$ is small. Moreover, when $\mathrm{\Delta }K$ increases, $\mathrm{\Delta }\mathrm{\Phi }$ will be more and more sensitive to $\mathrm{\Delta }K$, or say damages.

3.1. A quadrate thin cantilever plate

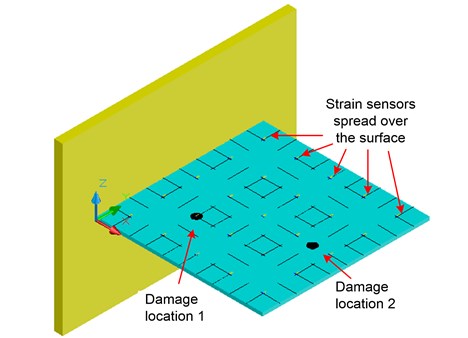
A numerical study on a steel quadrate thin cantilever plate with one edge fixed and the other three edges free, as shown in Fig. 1, is conducted to verify the strain mode based technique. The cantilever plate dimensions 1000 mm×1000 mm×10 mm. The materials properties are set as $E=$ 19.5×10¹⁰·N/m², $\rho =$7850 kg/m³, $\mu =$ 0.3. Uniaxil strain gagues are spread over the top surface of the plate along $X$ and $Y$ axis with spacing of 200 mm, also shown in Fig. 1.

As mentioned previously, damage patterns, e.g., rust holes, severe scratches, and crash pit damages, may exist in thin plate components of bridges, buildings, ships, etc., where the damages shall be emulated as physical stiffness loss in the damage vicinity. In the numerical study, stiffness reduction is placed as damage to a circular area with the radius of $40\mathrm{}\mathrm{m}\mathrm{m}$ in locations shown in Fig. 1. Different levels of damages are simulated by reducing the stiffness of this area for 10 %, 20 %, 30 %, 50 %, and 80 %, respectively. Both single and double damage cases are simulated. The black dots represent these two holes at damage location 1 and 2. Simulations are conducted through a commercial FEM program ANSYS 10.0 [18].

Fig. 1A quadrate thin cantilever plate (1000×1000×10 mm, E= 19.5×1010 N/m2, ρ= 7850 kg/m3, μ= 0.3)

Structural displacement and strain mode shape are obtained through the eigenvalues analysis. Table 1 shows the natural frequencies of the first five modes. The first displacement mode shapes with and without the single-hole damage, are shown in Fig. 2(a) and (b). In the same manner, the $X$-direction strain mode shapes with and without the single-hole damage are shown in Fig. 3(a) and (b).

3.2. Modal analysis of intact and damaged plate

For demonstrating the applicability of present method, simulated data will be used instead of measured data. Thus a great many of measurement points can be implemented using finite element method to get more sufficient strain values and displacement values. These points are placed every 20 mm over the surface of the plate, so there are 49×49 internal measurement points. The first displacement mode shapes of intact state and damaged state are obtained and shown in Fig. 2(a) and (b) while the first strain mode shape in Fig. 3(a) and (b), respectively. In these figures, the $X$ and $Y$ axes indicate the position on the plate, and the Z-axis presents the relative mode shape value. All the mode shapes have been normalized to a uniform scale. As shown, the first mode is a bending mode. The first five order frequencies for intact and damaged structures as well as their damage ratios are also shown in Table 1. As shown, the frequency change ratios are less than 2 %.

Through the comparison of Fig. 2(a) and (b), it is indicated that the displacement mode is insensitive to this type of damage: no obvious abnormality can be observed even at the circumferences of the holes. However, for the strain mode, obvious diversity can be seen between Fig. 3(a) and (b) in the damage position, although they are of quite similar shape. In order to verify the capability of modal parameters for damage identification, further research is to be carried out.

Fig. 2The first order displacement mode shape

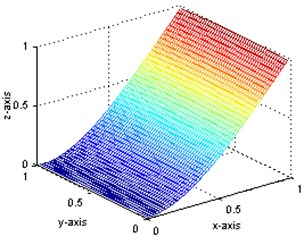
a) The displacement mode shape of intact plate

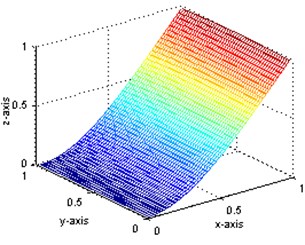
b) The displacement mode shape of damaged plate

Fig. 3The first order strain mode shape

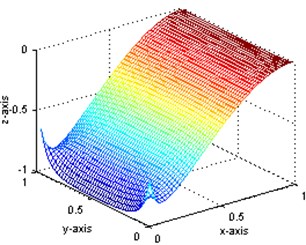
a) The strain mode shape of intact plate

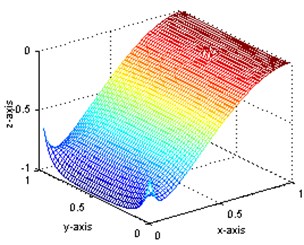
b) The strain mode shape of damaged plate

Define the differences of the mode shapes before and after damage as the damage index, similar conclusion can be drawn in the similar manner. Fig. 4 shows the change of the first five displacement modes and Fig. 5 shows the change of the first five strain modes.

As shown in Fig. 4, although the change of the first three displacement mode can clearly locate the damage position, the changes of the 4th and 5th displacement mode are so confused for damage localization and the index peaks value is quite small which is hard to detect. Contrastively, the changes of the all five stain modes shown in Fig. 5 have the largest value at the damaged points and a smaller value at the adjacent-to-damage element. The value is very small at points far away from the damaged points. This observation is consistent with the previous observation from Figs. 2 and 3: the index defined from the strain mode shape can give stronger indication of damage location than that from the displacement mode change. The peak values, 0.0042 shown in Fig. 4 and 0.063 shown in Fig. 5 for mode 1, also provide strong evidence for the sensitivity of strain mode shape.

Fig. 4Comparisons of displacement mode shapes: mode 1 to 5

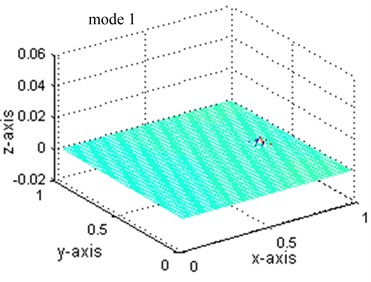
a)

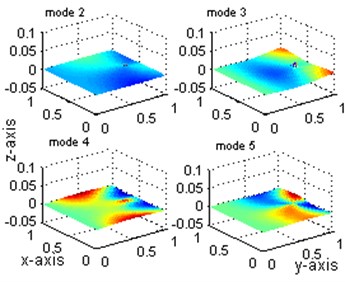
b)

Fig. 5Comparisons of strain mode shapes: mode 1 to 5

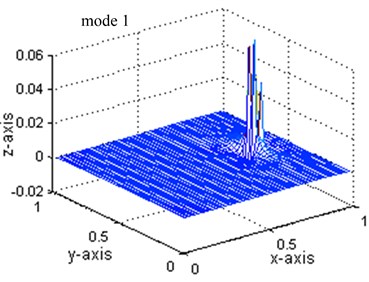
a)

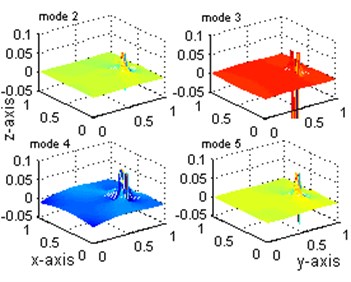
b)

4.1. Damage localization at single and multiple point

For practical applications, obtaining adequate and accurate enough information from only a small quantity of measurement points is a key problem for damage identification methods. In this study to determine a reasonable and effective schematic for placement of measurement points, only 3×3 measurement points are settled in the plate tentatively. Theoretically, the values on the edge of the plate are always around zeros, so it is meaningless to set measurement points at edges. Whether it can afford the damage identification effectively determines the feasibility of this method. Only the first order strain mode shape is discussed below.

Under this sensor placement, the following three damage case scenarios are assumed:

I) The damage occurs only in location 1 (see Fig. 1) with the stiffness decreased by 10 % to 80 %;

II) The damage occurs only in location 2 with the stiffness decreased by 10 % to 80 %;

III) The damages occur in location 1 and location 2 with the same damage degree from 10 % to 80 %.

Fig. 6Indices of various damage scenarios from sparse measurement points

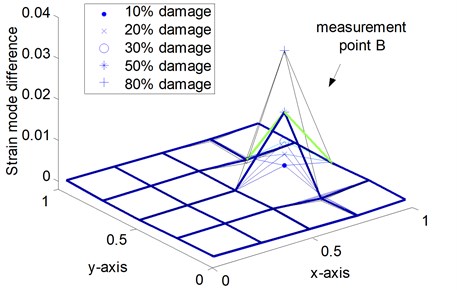
a) Case I: single point damage at location 1

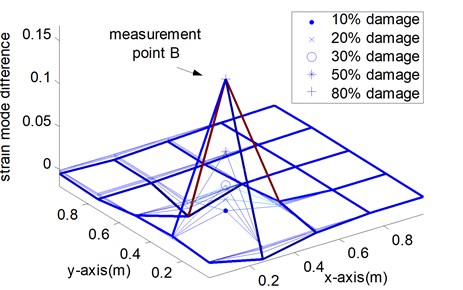
b) Case I: single point damage at location 1

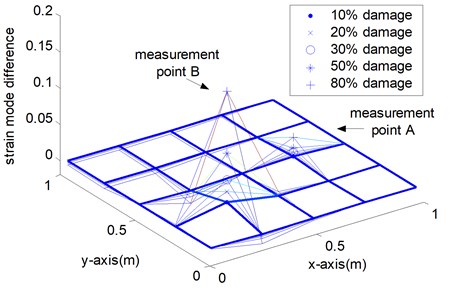
c) Case III: multiple point damage at location 1 and 2

Figure 6 shows the measured strain mode changes in accordance with the three damage cases, which exhibit the following properties. Firstly, the maximum of the index appears at the point around the defective area. However, in the other measurement points, the value changes little. No matter which mode is selected for the analysis, the damage location can always be identified correctly in the numerical simulation. Secondly, when the damage position changes, this damage localization method still works. The damage location can be fixed in the range near the peak point. Thirdly, in Fig. 6 (c), the index values at two damage positions are the sum of the values of measurement point 1 and measurement point 2 respectively. Taking notice of equation (3) and Table 1, when $\mathrm{\Delta }\lambda$ is small, multiple damage with different location rarely affect each other and could be detected respectively. Thus, the strain mode change could be a meaningful indicator for damage localization.

4.2. Damage quantification

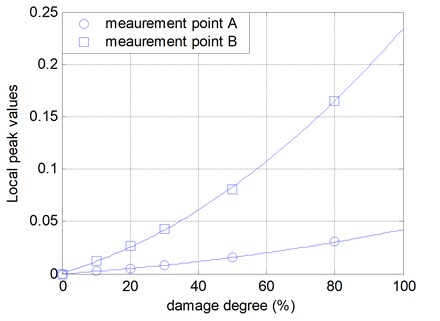
The index peak values of case III are shown in Fig. 7. As the damage grows from 0 % to 80 %, the peak values increase accordingly. As shown in this figure, when $\mathrm{\Delta }K$ is small, the strain mode change can be regarded as the linearly increased along with the increase of the stiffness changes. The nonlinearity observed when the damage degree is beyond 50 percent is due to that when the damage is severe the change of stiffness matrix $\mathrm{\Delta }K$ can not be neglected. In this point, it can be used as a measure of damage extent.

Fig. 7Local peak values of strain mode shape difference