Arterial pulse transit time evaluation by peripheral pulse wave measurement

1. Introduction

Cardiovascular diseases remain the biggest causes of deaths worldwide. Early determination of cardiovascular diseases is background for population health. Many cardiologists are pointed that 24 h continuous monitoring at usual environment provides more useful and valuable information for early diagnosis than periodic ambulatory survey. For continuous 24 h monitoring device must be simple to use and comfortable. For such devices photopletysmographic sensors commonly is used [1].

The stiffening arteries are a potential risk factor for increased cardiovascular morbidity and mortality. Pulse wave velocity (PWV) or pulse transit time (PTT) has been identified as a promising approach in continuous non-invasive systemic arterial tree functional statement evaluation. The most popular measurement technique involves a one-lead ECG and a photoplethysmographic (PPG) clip at a finger, toe or ear, because the ECG is more easily accessible [2, 3]. It would be much more desirable if such monitoring could be made on a beat-to-beat basis, because PTT can fluctuate considerably, not only over a long period of time but also in a very short term.

In ambulatory practice commonly PTT is used as PWV estimator because trough length of artery between two distance points remains unknown. PTT is time delay form ECG R peak and foot of peripheral pulse wave (PPW). The sensor measurements are assumed to be available only at a peripheral part, such as a finger, to minimize the influence on patients daily life therefore this technique is not most appropriate for wearable monitoring systems realization because least three sensors and two measurement devices (ECG and PPG) is needed. Therefore most convenient technique is required for PWV estimation.

One of methods for PTT evolution from photoplethysmographic pulse has been proposed by authors. In this case PTT is evaluating as time delay between first and second peeks of PPW measured by PPG. Depending on the measurement point or arterial stiffness second peek is not appreciable. In physical activity periods PPW diastolic portion is corrupted by movement artifacts and determination of second peak is very problematic. If these situations come together determination of second peak is impossible.

This paper presents new indices which are able to change PTT and links closely with the development of wearable sensors of cardiovascular function, but the realm of application of such models is much broader than this single task.

2. Theory

At systole period of cardio cycle pressure in artery rapidly growth and disturb arterial diameter. This deformation pulse wave (DPW) spread along arterial system to periphery. This DPW has axial velocity defined by Moens-Korteweg equation [4]:

where $v_x$ – axial DPW velocity, $E$ – arterial Young’s modulus, $h$ – arterial wall thickness, $\rho$ – blood density, $l$ – length of arterial cross section arc in unstressed condition.

When DPW propagate toward to periphery arterial wall starts to oscillate perpendicular to propagation direction. In this way radial pulse wave at point comes and it has radial velocity $v_r$. Longitudinal DPW velocity $v_x$ describes Moens-Korteweg equation (1) and shows that the $v_x$ is function of Young’s modulus. By analogy with the elastic string like in Hook’s law we will show that radial pulse wave velocity also is Young’s modulus function. When the external force acts perpendicular to the string it is displaced from start position and stores potential energy. At the string going back to the equilibrium position the potential energy transforms into kinetic energy. Total energy of oscillating system is:

where $W_p$ – potential energy, $W_k$ – kinetic energy, $k$ – stiffness coefficient, $m$ – body mass density, $\Delta l$ – displacement amplitude.

In maximal deformation case $(\Delta l_{\mathrm{m}\mathrm{a}\mathrm{x}}=M)$$W_k=0$, $W_p=\mathrm{m}\mathrm{a}\mathrm{x}$:

Spring radial oscillation velocity at measurement point:

where $v_r$ – radial velocity.

According with equation (4) radial velocity depends on spring stiffness $k$. We expose that spring stiffness in physical means is analogous to arterial wall Young’s modulus $E$ and equation (4) can be used for arterial wall radial velocity evaluation. Tensile strength (external force) $F_t$ acting on the body internal or stress force with same magnitude and opposite direction arises $(-F_i=F_t)$. Relationship $\left(F_i/l\right)$ is stiffness $k$. In consideration of stiffness dimension $\mathrm{d}\mathrm{i}\mathrm{m}\left(k\right)=\left[N/m\right]$ we rewrite Hook’s law:

where: $l$ – string length, $F_t$ – tensile strength (external force), $F_i$ – internal force.

Cross sectional diameter and arc length $l=2\pi \times r$ are varying with changing pressure in artery. The ratio of force $F_t$ acting to the inner arterial surface area is pressure $p=F_t/S$. It changes artery cross section arc length. Inner force acts to the same surface area and is called stress $\sigma =F_i/S$. Equation (5) can be rewritten:

In equations (5, 6) stiffness has analogously expressions. At (5) coefficient $k$ represents tensile strength whose acting to point $\left(S=\underset{r\to 0}{\lim \left(\pi \cdot r^2\right)}\right)$ challenge 1 meter elongation and at (6) this coefficient represents stress whose acting to area of stick challenge 1 meter elongation. Arterial wall like string stiffness depend on its geometry: inner arc length $l_i$, external arc length $l_e$ and wall thickness $h$ [6]:

By substituting (7) to (6) we have:

Dimensions in (8) at left and right sides do not mach. Deformation is commonly represented with non-dimensional units. By dividing $\left(\Delta l/l\right)$ we have relative deformation $\epsilon$ and restore dimension equality:

Arterial and string stiffness in physical means is coinciding and differ by constant value that depend on geometry. In equation (4) stiffness parameter substituting by artery Young’s modulus we have arterial wall displacement velocity equation:

where $v_r$ – radial DPW velocity, $l$ – cross sectional arc length at diastole, $\Delta l$ – cross sectional arc length difference between systole and diastole.

3. Modeling

As depicted at previous chapter the arterial stiffness is function not only of arterial wall properties, arterial geometry, but also depends on driving arterial pressure (7). This fact also confirmed by other researches [7]. Commonly Moens-Korteweg equation (1) is used for longitudinal DPW velocity evaluation versus arterial pressure because arterial wall material is not changed through measurement period [8].

Flow generator. As heart contracts blood mass from left ventricle is pushed to arterial system with flow rate $Q\left(t\right)$. We can assume that input impedance $Z$ is constant and flow rate is:

were $p\left(t\right)$ – arterial pressure, $Z$ – input impedance of arterial system, $Q\left(t\right)$ – blood flow rate.

Blood flow rate is described by equation:

were $q_0$ – is the cardiac output and $\tau$ – is the time at which the maximal cardiac output is reached, $T$ – cardio cycle period (heart contraction period).

Systemic arterial tree model. Arterial system electric analog model (Fig. 1), [9] defines relationship between blood flow $Q$ as input arterial system and arterial pressure $p$ (Fig. 1c), who act to the arterial wall. In model used these electrical analogs: blood flow represented as electrical current; arterial pressure as voltage; R1 represents the resistance due aortic valve (in other words systemic vascular resistance) $\mathrm{d}\mathrm{i}\mathrm{m}\left(R\right)=N/m^{4}s$; R2 represents peripheral vascular resistance; C1 – systemic vascular compliance $\mathrm{d}\mathrm{i}\mathrm{m}\left(C\right)=kg/m^4{s}^2;$C2 – peripheral vascular compliance; L – blood flow inertance $\mathrm{d}\mathrm{i}\mathrm{m}\left(L\right)=kg/m^4.$ Arterial pressure variation in vascular system Fig. 1b describes equation:

Fig. 1a) Blood flow rate, b) model of systemic arterial tree, c) arterial pressure p(t). 1 mm Hg = 133.3 N/m2

Arterial transfer function. Artery diameter is changing by acting pressure. DPW as response to acting pressure has been calculated according with arterial wall transfer function (Fig. 2b). Arterial transfer function has been obtained from data depicted in [10].

Fig. 2a) Arterial pressure, b) arterial wall transfer function p(t) vs. d(t), c) arterial diameter. 1 mm Hg = 133.3 N/m2

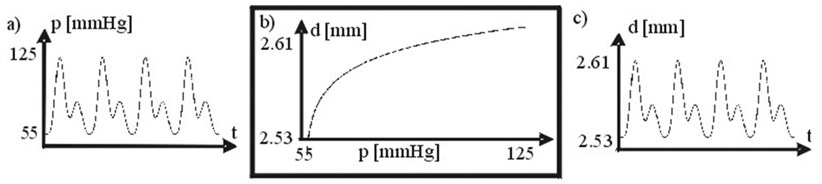
During cardiocycle period longitudinal DPW velocity $v_x$ is constant and radial DPW velocity $v_r$ at measurement point is varying. For comparison of those two quantities in time maximal radial velocity values were selected.

Model based investigation. Aim of the simulation is to investigate correlation between longitudinal DPW and radial DPW at measurement point. For this purpose modeling was being done. Arterial system input signal was modeled as fifteen periods varying amplitudes of blood flow waves. Each period consists from two parts. First part is $\tau$ seconds duration and named systole. At systole blood folow exceeds maximal amplitude $q_0.$ Second part is named diastole. In diastole heart valve is closed and blood flow rate is zero. First and last five periods of modeled blood flow waves has amplitudes $q_0=$ 450 ml/s. Middle five periods of modeled blood flow waves has amplitudes $q_0=$ 400 ml/s Arterial pressure values $p\left(t\right)$ have been obtained in accordance with (13) and DPW in accordance with arterial transfer function (Fig. 2b).

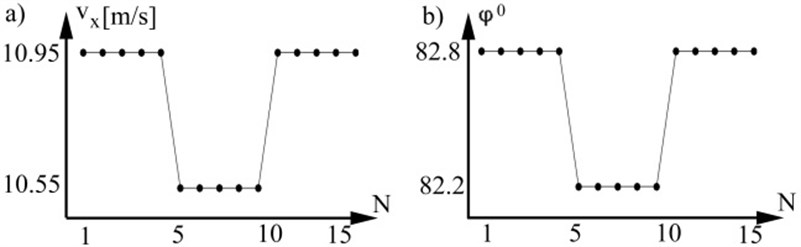
At each heart beat we have one DPW speed value because it is calculated at each beat as the time delay between two distal points, therefore longitudinal velocity values $v_x$ become function of beats number $n$. Values of $v_x$ are calculated by substituting maximal amplitudes of pressure to the equation (1) from each simulated period. Radial DPW velocity $v_r$ (Fig. 3a) was calculated according to (7, 10) by substituting pressure values. The most popular measurement technique for pulse wave acquiring is a photoplethysmographic (PPG) clip at a finger. Different PPG devices have different amplify coefficient, therefore radial velocity of DPW was calculated from normalized DPW amplitudes and expressed in degree $\varphi$ (Fig. 3b). For comparison $v_x$ and $\varphi$ a maximal value from each period was acquired. Modeling has demonstrated that $v_x$ and $v_r$ are changing at the same time principle and have linear correlation.

Fig. 3a) Axial DPW velocity, b) radial DPW by degree

4. Experiment setup

For evaluation of simulation results (Fig. 3) experimental system was created. This system consists from photoplethysmographic clip, one channel electrocardiograph, 12 bit ADC and data acquisition software. Photoplethysmographic clip has light source (light emitting diode with wave length 880 nm) and photo detector. Light energy propagates through tissues and blood vessels. Largest amount of light is absorbed by tissues and remains partly reflected from arterial wall and falls into the photo detector. Base line variation of photo current is proportional to light absorption by tissues and small amplitude alternate photo current is proportional to the inner arterial diameter. This small amplitude alternate photo current is called photopletysmographic pulse wave PPW. In order to find DPW velocity PPW must be measured at two with known distance distal points. Because arterial length between measurement points still is unknown the time delay between ECG $R$ peak and PPW foot is commonly used.

At the time of experiment ECG and PPW signals were measured. For PPW foot point recognition algorithms were used. After pulse transit time (PTT) time delay between ECG $R$ peak and PPW foot was calculated. Length of signal records is defined by numbers of heart beats $N_{RR}$.

For examination of time variation principle of the PTT and initial rise velocity of the PPW veloergonometric tests were done. Experiment was divided in three stages. At first stage patient is sitting on the bicycle. Three minutes ECG and PPW signals are collected. At the second stage patient performs a physical test. ECG and PPW signals are not collected. At the third stage patient is at the rest. ECG and PPW signals are collected as long as achieves initial heart rhythm. After test data analysis was done.

5. Results and conclusions

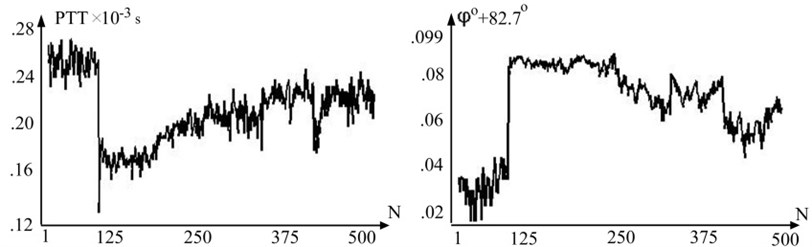
We included five patients (mean age 27±5) free of cardiovascular treatment were measured. Representative $\mathrm{P}\mathrm{T}\mathrm{T}\left(n\right)$ and $\varphi \left(n\right)$ waveform (Fig. 4) show that PTT and radial velocity $\varphi \left(n\right)$ vary in opposite directions but has same curve form. Cross correlation coefficient of $\mathrm{P}\mathrm{T}\mathrm{T}\left(n\right)$ and $\varphi \left(n\right)$ is –93.4±5.6 and confirms linear dependency between longitudinal and radial velocity when pressure varies in physiological range.

Fig. 4Representative variation of pulse wave transit time (PTT) and variation of radial velocity by degree in one subject throughout the test

To compare PTT and VIR first stage of veloergonometric test data was analyzed. PTT and VIR were expressed in different dimensions. PTT has dimension expressed in seconds and radial velocity was expressed in degrees. To compare those quantities their values were normalized. After normalization PTT gain values from interval $0\le \mathrm{P}\mathrm{T}\mathrm{T}\left(n\right)\le 1$ and VIR gain values from interval $0\le \varphi \left(n\right)\le 1$. PTT and VIR results are presented in Table 1.

If in the first stage (Fig. 4) ($1\le n\le 125$) variability of $\mathrm{P}\mathrm{T}\mathrm{T}\left(n\right)$ and $\varphi \left(n\right)$ values about base line is almost the same than in the third stage (Fig. 4) ($125\le n\le 500$) $\varphi \left(n\right)$ values variability about the base line is smaller. This can be explained because front end of arterial pulse wave is less influenced by movement artifacts. Significant values of VIR (82-83 degree) can be explained by arterial wall property which leads to rapid change of arterial pulse wave in initial part of systole period when pressure change is small [12].

The modeling and experimental investigation results indicate that PTT may be replaced by VIR values with proposed method and for wearable devices they are more appropriate.