Pounding of adjacent buildings considering pile-soil-structure interaction

2.1. Model of contact element for pounding

There are two main methods, stereo-mechanism and contact element approaches, which are usually used to investigate the pounding of buildings. The stereo-mechanical approach, which is based on the equalization of pounding energy and ignores the process of pounding, is usually applied to single degree-of-freedom mass-spring systems. The contact element approach is a force-based approach, in which a contact element is activated in the pounding point once impact occurs. Generally, there are four contact element models: linear spring, Kelvin model, Hertz model and Hertz-damp model. Among them, Hertz-damp model is the most precise one in simulating the pounding-involved structural response [5, 6]. In this paper, the Hertz-damp contact element is used to simulate the pounding of adjacent structures.

Fig. 1Hertz-damp contact element

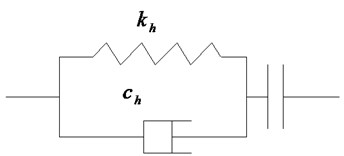
Fig. 1 shows the model of Hertz-damp contact element. A nonlinear spring is employed to simulate the pounding of adjacent building, and a nonlinear viscous damper is used to simulate the energy dissipation during the pounding. The impact force can be computed by:

where $u_1$ and $u_2$ are the displacements of two pounding adjacent buildings at the potential pounding position, respectively; $g_p$ is the separation distance of buildings, and $k_h$ is the nonlinear stiffness of impact element. Since the main purpose of this paper is to investigate the influence of PSSI on pounding, $k_h$ is assumed to a constant in this paper. $c_h$ can be obtained by:

where $\xi$ is the damping ratio. Assuming that the dissipated energy of structures during pounding are due to the damper, $\xi$ can be obtained by [13]:

Fig. 2Computational model of adjacent buildings

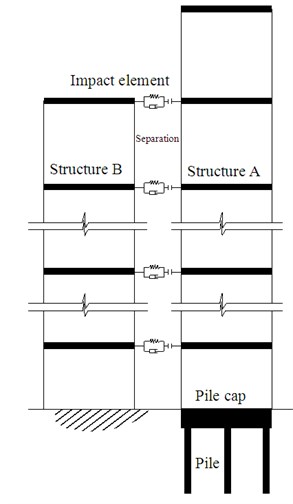
a) Adjacent buildings

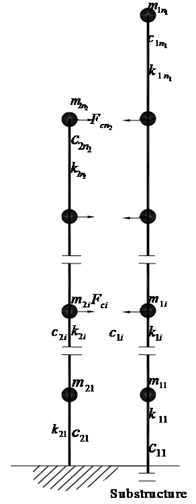
b) Model of superstructure

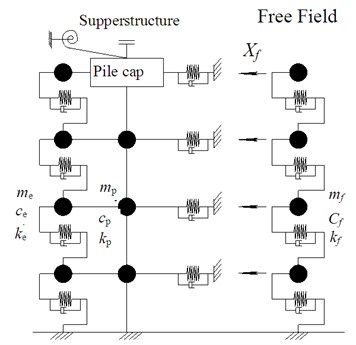
c) Model of pile

2.2. Model of adjacent structures with pile foundation

A system of two adjacent buildings and its corresponding model are shown in Fig. 2. Structure A is an $n_1$-story building with a pile foundation, and Structure B is an $n_2$-story building with a fixed foundation. Both the superstructure and the pile are simplified as multiple-degree-of freedom system. All of the piles are incorporated into an equivalent pile. An equivalent bending spring is applied on the location of pile platform to model the rotational stiffness. The soil surrounded the pile is simplified to equivalent spring-mass systems, and connects rigidly with the pile.

Base on the hypothesis and models, the motion equations of superstructure, substructure of Structure A can be expressed as:

where ${\mathbf{M}}_S$, ${\mathbf{C}}_S$ and ${\mathbf{K}}_S$ are $n_1\times n_1$ mass, damping and stiffness matrices of superstructure respectively; ${\ddot{\mathbf{X}}}_S$, ${\dot{\mathbf{X}}}_S$ and ${\mathbf{X}}_S$ are $n_1$-dimensional acceleration, velocity and displacement vectors of superstructure respectively; ${\mathbf{M}}_p$, ${\mathbf{C}}_p$ and ${\mathbf{K}}_p$ are $k\times k$ mass, damping and stiffness matrices of simplified pile model respectively; ${\ddot{\mathbf{X}}}_d$, ${\ddot{\mathbf{X}}}_d$ and ${\mathbf{X}}_d$ are $k$-dimensional acceleration, velocity and displacement vectors of substructure respectively; ${\mathbf{M}}_e$, ${\mathbf{C}}_e$ and ${\mathbf{K}}_e$ are $k\times k$ mass, damping and stiffness matrices of surround soil respectively; ${\ddot{\mathbf{X}}}_f$, ${\dot{\mathbf{X}}}_f$ and ${\mathbf{X}}_f$ are respectively k-dimensional acceleration, velocity and displacement vectors of unit soil column in free field; ${\ddot{x}}_g$ is the acceleration of ground; $c_{\theta }$ and $k_{\theta }$ are the rotational damping and stiffness of pile cap; $\theta$ is the rotational angle of pile cap; ${\mathbf{I}}_s$ and ${\mathbf{I}}_d$ are the identity vectors for super-structure and sub-structure respectively; H is an $n_1$ – dimensional height vector of building floors, ${\mathbf{F}}_C$ is the matrix of pounding force, and ${\mathbf{B}}_A$ is the location matrix of potential pounding location. Eqs. (4)-(6) can be written to an equivalent equation:

where ${\mathbf{M}}_A$, ${\mathbf{C}}_A$ and ${\mathbf{K}}_A$ are $m\times m$ mass, damping and stiffness matrices of system A respectively;${\ddot{\mathbf{X}}}_A$, ${\dot{\mathbf{X}}}_A$ and ${\mathbf{X}}_A$ are respectively $m\text{-}\text{dimensional}$ acceleration, velocity and displacement vectors of Building A; $m$ is the degrees of freedom of the system, and $m=n_1+k+1$; ${\ddot{\mathbf{X}}}_{fgA}$ is the acceleration vector of free field input. The matrices can be expressed as:

Similarly, the motion equation of Structure B is expressed as:

where ${\mathbf{M}}_B$, ${\mathbf{C}}_B$ and ${\mathbf{K}}_B$ are mass, damping and stiffness matrix of Structure B respectively; ${\ddot{\mathbf{X}}}_B$, ${\dot{\mathbf{X}}}_B$ and ${\mathbf{X}}_B$ are acceleration, velocity and displacement vectors of Structure B respectively; ${\mathbf{I}}_B$ is the identity vectors for Structure B. Eqs. (7) and (8) can be rewritten as:

where $\mathbf{M}=\left[\begin{array}{cc}{\mathbf{M}}_A& \\ & {\mathbf{M}}_B\end{array}\right],\mathbf{K}=\left[\begin{array}{cc}{\mathbf{K}}_{\mathrm{A}}& \\ & {\mathbf{K}}_{\mathrm{B}}\end{array}\right],\mathbf{}\mathbf{}\mathbf{C}=\left[\begin{array}{cc}{\mathbf{C}}_A& \\ & {\mathbf{C}}_B\end{array}\right],$

${\mathbf{B}}_s=\left[\begin{array}{cc}{\mathbf{B}}_A& {\mathbf{B}}_B\end{array}\right],{\ddot{\mathit{X}}}_{fg}=\left[\begin{array}{cc}{\ddot{\mathit{X}}}_{fgA}& {\mathbf{I}}_B{\ddot{x}}_g\end{array}\right].$

And $\ddot{\mathbf{X}}$, $\dot{\mathbf{X}}$ and $\mathbf{X}$ are the acceleration, velocity and displacement vectors of system, respectively.

2.3. Responses of unit soil column

A unit area of soil column is considered as the model of free field. Assuming that the soil of free field is divided into $s$ layers from top to bottom, the equivalent lumped mass is:

where $h_i$ and ${\rho }_i$ are the height and density of $i$-th layer soil. The horizontal stiffness of $i$-th layer is:

where $G_i$ is the shear module of $i$th layer. The damping matrix of unit soil column ${\mathbf{C}}_f$ is expressed in Rayleigh damping as:

where ${\mathbf{\alpha }}_f$ and ${\mathbf{\beta }}_f$ can be calculated by:

where $i=$ 1, …, $s$; ${\zeta }_i$ is the damping ratio of $i$-th layer. Thus, the dynamic motion of unit soil column is:

This motion equation can be solved by Newmark method. The result is then used excitation acceleration vector in Eq. (7).

2.4. Mass, stiffness and damping of equivalent soil column

During the vibration of pile, the soil which surrounds the pile also vibrates. Assuming the area of vibrating soil is equal to the area of pile cap, the mass of additional vibrating soil can be approximated as:

where $\rho$ is the density of soil; $A$ is the area of plat cap; $h_i$ is the height of $i$-th layer of soil.

Based on Mindlin method, the horizontal stiffness of soil can be calculated approximately by [14]:

where, $E\left(z_i\right)$ is the Young's modulus of soil in the depth of $z_i$; $L_i$ is the length of $i$-th pile segment.

The horizontal damping of soil can be obtained by:

where $R_p$ is the radius of pile; $h_i$ is the height of $i$-th layer of soil; $v_p$ is the velocity of $P$ wave; $v_s$ is the velocity of shear wave. They can be expressed as:

where $\mu$ is the Poisson’s ratio; $G$ is the shear modulus.

3.1. Time history of pounding

The structural responses histories of 4 cases: (1) no pounding with PSSI; (2) no pounding without PSSI; (3) pounding with PSSI; (4) pounding without PSSI, are obtained and shown in Figs. 3-10.

Fig. 3 shows the roof displacement of Structure A when its foundation is assumed to be fixed. It can be seen that the roof displacement in pounding case (case 4) is about 15 % smaller than that in no pounding case (case 2) when the PSSI of Structure A is not considered. The main reason is that the free vibration of Structure A is blocked by Structure B in pounding location, which results in the decrease of roof displacement. Fig. 4 and Fig. 5 are roof displacement of Structure A. They show that the influence of PSSI on roof displacement of Structure A in no pounding case (Fig. 4) is relatively small (less than 10 %), but the influence of PSSI on displacement of Structure A in pounding case (Fig. 5) is very large. The displacement in case 3 is nearly 50 % larger than that in case 4. The main reasons are: (1) when the PSSI is considered, the difference of natural frequency between Structure A and Structure B increases. Thus, the asynchronous vibration of adjacent buildings becomes violent and the pounding of adjacent buildings will happen easily; (2) when the PSSI is considered, the lateral stiffness of Structure A decreases. Hence the separation distance of adjacent buildings becomes relatively insufficient, and the pounding of adjacent buildings will be violent.

Fig. 3Response history of roof displacement of Structure A without PSSI

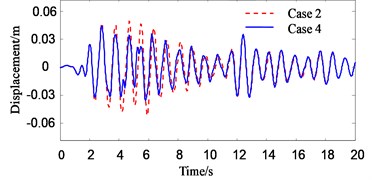
Fig. 4Response history of roof displacement of Structure A (in no pounding case)

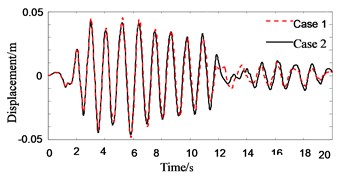
Fig. 5Response history of roof displacement of Structure A (in pounding case)

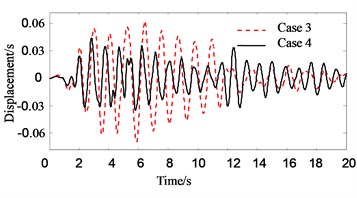
Fig. 6Response history of top floor displacement of Structure B

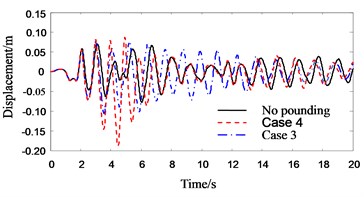
Fig. 7Response history of roof acceleration of Structure A without PSSI

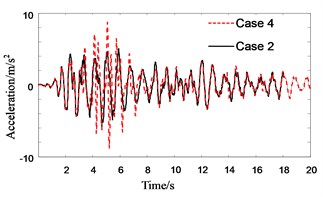
Fig. 8Response history of roof acceleration of Structure A (in no pounding case)

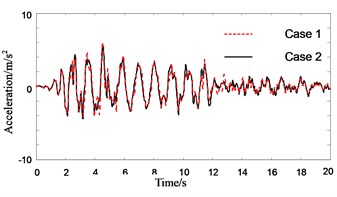
Fig. 9Response history of roof floor acceleration of Structure A (in pounding case)

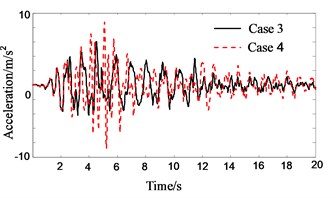
Fig. 10Response history of roof acceleration of Structure B

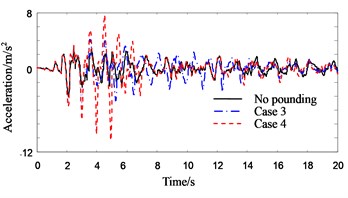
Fig. 6 shows the roof displacement of Structure B. Unlike Structure A, the roof displacement of Structure B with PSSI consideration is about 60 % smaller than that without PSSI consideration. The reason is that the Structure A becomes flexible when the PSSI is considered. Thus, the pounding force weakens and the pounding pulse wanes.

Figs. 7-9 show the response histories of roof acceleration of Structure A. From Fig. 7 it can be seen that the pounding pulse of acceleration is very obvious when the PSSI is not considered. The acceleration in pounding case is about 55 % larger than that in no pounding case. The influence of PSSI on the acceleration response in no pounding case is relatively small (Fig. 8). But it is very obvious on the acceleration response in pounding case. The roof acceleration in case 3 is 35 % smaller than that in case 4 (Fig. 9). This is probably due to the reason that the Structure A becomes more flexible and the pounding force weakens when the PSSI is considered. Similarly, the roof acceleration of Structure B in case 3 is much smaller than that in case 4 (Fig. 10).

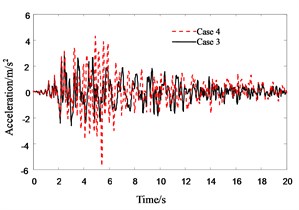
Figs. 11-16 show the response histories of 4th floor acceleration and displacement of Structure A. They show the similar trends to those of roof floor, the only difference between them is that their peak values of 4th floor are some smaller than those of roof floor.

Fig. 11Response history for 4th floor displacement of Structure A without PSSI consideration

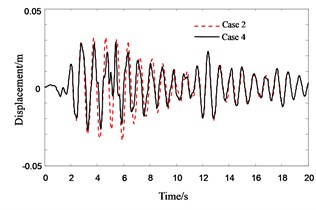
Fig. 12Response history for 4th floor displacement of Structure A in no pounding cases

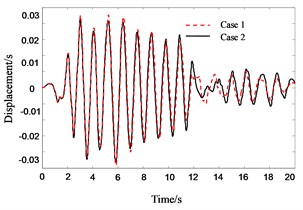
Fig. 13Response history for 4th floor pounding displacement of Structure A in pounding cases

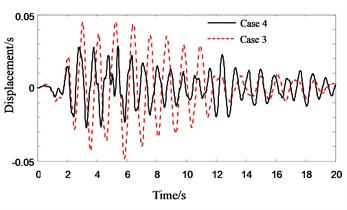
Fig. 14Response history for 4th floor acceleration of Structure A without PSSI consideration

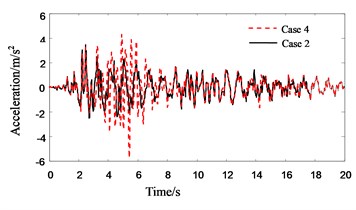
Fig. 15Response history for 4th floor acceleration of Structure A in no pounding cases

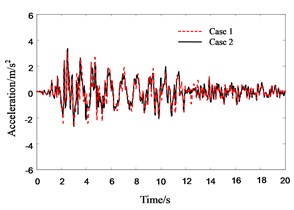
Fig. 16Response history for 4th floor acceleration of Structure A in pounding cases

3.2. Influence of separation distance

The separation distance between adjacent buildings plays an important role on their pounding during earthquake. In order to investigate the influence of separation distance on the pounding behaviors of adjacent buildings, all conditions except the separation are assumed unchanged. The response histories of the system with varied separation distance are computed.

Fig. 17 shows the relationship between the peak displacement of roof floor and separation distance. It can be seen that if the foundation of Structure A is assumed to be fixed, the pounding displacement of Structure B decreases rapidly with increasing separation distance in the beginning, and then it becomes flat gradually. When the separation distance approaches 0.08 m, the displacement tends to be a constant value. The roof displacement of Structure A increases initially, and then decreases gradually with increasing separation distance. When the separation distance approaches 0.06 m, the displacement approaches a constant value. The maximum value of displacement is observed when the separation distance is about 0.04 m. If the PSSI of Structure A is considered, the roof displacements of both Structure A and B decrease with increasing separation distance, but maximum values of roof displacement are also appear at the separation distance of 0.01 m and 0.03 m respectively. It should be noted that the maximum roof displacement of Structure B happen in about 0.13 m when the foundation of Structure A is fixed, which is much larger than that of both Structure A and Structure B in any other cases. The main reason for this observed behavior is that the roof displacement is affected by the stiffness, velocity and acceleration of structures. Between the two pounding structural bodies, the one with softer stiffness gets the larger response after pounding. When the foundation of Structure A is fixed, the stiffness of Structure B is much softer than that of A. Thus Structure B has the larger pounding responses. Generally, the larger the vibrating velocity and acceleration are, the bigger the pounding response will be. When separation distance is small, the acceleration becomes very large and the velocity becomes very small. But when separation distance is large, the velocity becomes very large and the acceleration becomes very small. When the separation distance is large enough, the pounding of adjacent buildings will not happen, and the displacement of buildings tends to a constant value. Hence, there exists a separation distance where the roof displacement has the maximum value.

Fig. 17The relationship between roof displacement and separation distance

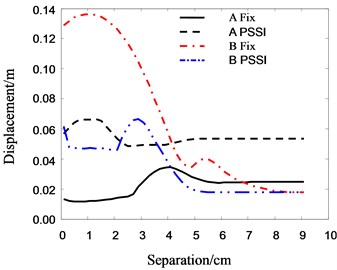
Fig. 18The relationship between acceleration of top floor and separation distance

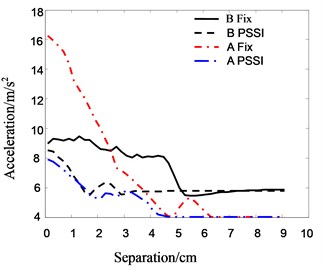
Fig. 18 is the relationship between the peak acceleration of roof floor and separation distance. It can be seen that when the foundation of Structure A is fixed, the accelerations of both Structure A and B decreases gradually with increasing separation distance initially. The acceleration responses tend to a constant value when the separation distance approaches about 0.05 m and 0.06 m in Structure A and B respectively. When the PSSI of Structure A is considered, the accelerations of both Structure A and B decrease gradually, and then tend to a constant value as separation distance increases. This trend is similar to displacement in pounding case. The main difference is that the maximum acceleration is observed when separation distance is zero. The reason is that the roof acceleration response depends mainly on the vibrating acceleration and stiffness of structures, and the vibrating acceleration has the maximum value when the separation distance approaches zero.

3.3. Influence of pounding stiffness

The stiffness of Hertz-damp pounding element, named as pounding stiffness, not only influences the pounding force of adjacent buildings, but also influences the energy dissipation during pounding. To study the influence of pounding stiffness on the pounding response of buildings, it is assumed that all conditions remain unchanged except the pounding stiffness. The responses histories of system with different pounding stiffness are computed and the maximum values of pounding displacement and the acceleration in roof are obtained.

Fig. 19 shows the relationship between the roof displacement and the pounding stiffness. It can be seen that the pounding stiffness plays a significant role on the roof displacement of Structure B when the foundation of Structure A is fixed. At the beginning, the roof displacement of Structure B increases quickly with increasing pounding stiffness. As the increase of pounding stiffness, the peak roof displacement becomes stationary. On the other side, the influence of pounding stiffness to Structure A is not very obvious. This is because the stiffness of Structure B is much smaller than that of Structure A, and it is less sensitive to the pounding stiffness. When the PSSI of Structure A is considered, the peak roof displacement of Structure A increases gradually and that of Structure B decreases gently as pounding stiffness increases. This is because the pounding displacement of smaller stiffness structure relies mainly on the stiffness of itself, and that of larger stiffness structure relies mainly on the stiffness of pounding.

Fig. 19The relationship between roof displacement and pounding stiffness

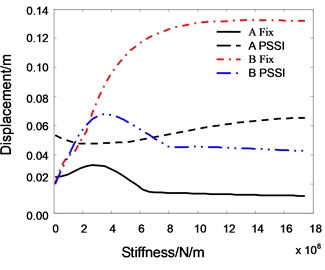
Fig. 20The relationship between roof acceleration and pounding stiffness

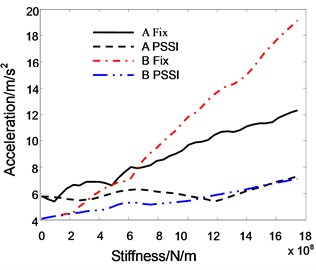
Fig. 20 shows the relationship between the peak acceleration of roof and the pounding stiffness. When the PSSI is not considered, the pounding accelerations of both A and B increase gradually with increasing pounding stiffness. When the PSSI of Structure A is considered, the influence of pounding stiffness is not obvious. It shows that the acceleration response of structure with smaller stiffness is sensitive to the pounding stiffness.

3.4. Influence of period ratio

If the periods of Structure A and B are $T_A$ and $T_B$ respectively, the period ratio is defined as $T_A/T_B$. To investigate the influence of period ratio on the pounding of adjacent buildings, the stiffness of Structure A is scaled by coefficients. Thus the period ratio is changed by coefficients. Assuming that all other conditions remain unchanged, the curves of the maximum displacement and acceleration of roof floor varied with the period ratios are obtained as shown in Figs. 21-22.

From the figures it can be seen that the period ratio of adjacent buildings has a significant influence on the pounding response. As we know, the pounding of adjacent buildings is caused by their asynchronous vibration. When the period ratio approaches to 1, their vibrations are synchronous. Hence the buildings don’t collide with each other, and their responses are relatively small. When the period ratio approaches to 0.5, the displacement and acceleration response of Structure B are quite large. The maximum acceleration reaches 20 m/s², and the maximum displacement reaches 0.3 m. It is perhaps because the vibration phases of two buildings are contrary in this case.

Fig. 21The relationship between roof acceleration and period ratio

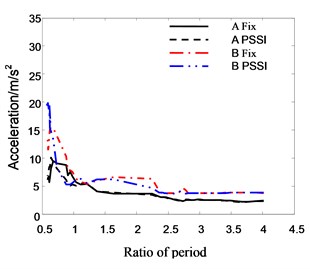
Fig. 22The relationship between roof displacement and period ratio

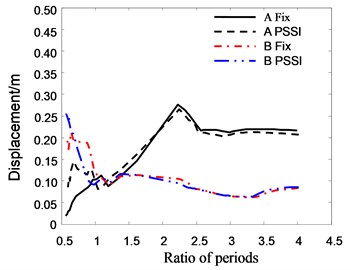
Fig. 23The relationship between the response factor of top floor in Structure A and inertia moment of pile section

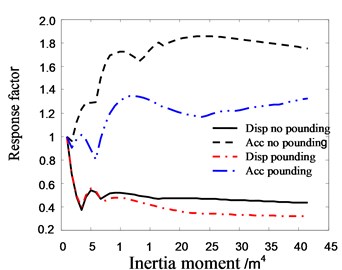
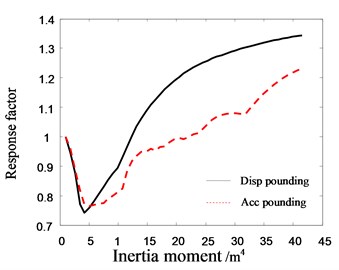
Fig. 24The relationship between the response factor of top floor in Structure B and inertia moment of pile section

3.5. Influence of pile stiffness

The stiffness of piles is one of the most important factors influence the PSSI. The response factor is defined as the ratio of structural response with different pile-cross-section to the response with pile-cross-section moment of inertia of 1 m⁴. Assuming that all other conditions remain unchanged, the relationship between the response factors in roof floor of structure and the pile-cross-section’s moment of inertia are computed.

Fig. 23 shows that as the increase of inertia moment, the displacement of Structure A decreases in the beginning and then stabilize gradually. The acceleration of Structure A increases in the beginning, and then approaches to constant. At the same time, the difference of response factors between pounding and no pounding increases gradually as the increase of inertia moment, which means the influence of pile inertia moment on pounding increases. The main reason is that the increase of pile inertia moment strengthens the global stiffness of structure and results in the exacerbation of structural pounding. It can be seen from Fig. 24 that the response of Structure B decreases sharply in the beginning, and then increases gradually as the increase of inertia moment. It also shows that the rigid pile can aggravate the pounding of adjacent building.

Fig. 25The relationship between the response factor of Structure A and velocity of shear wave

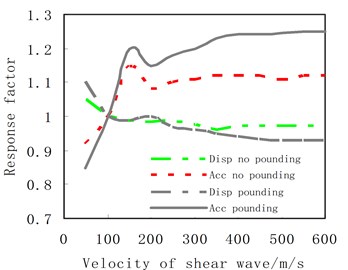
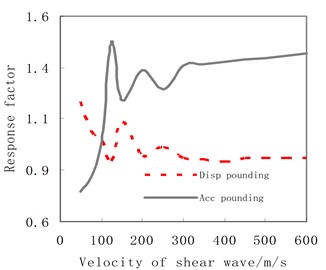
Fig. 26The relationship between the response factor of Structure B and velocity of shear wave

3.6. Influence of soil’s shear wave velocity

The types of construction sites can be classified by the equivalent shear-wave velocity and the layer thickness of soil. In order to investigate the influence of shear-wave velocity on the pounding, it is assumed that all other conditions remain unchanged and the ground is composed of a single soil type. The response factors, which is defined in this subsection as the ratio of peak responses with different soil to the response with the soil of shear-wave-velocity equaling 100 m/s, are obtained and shown in Figs. 25 and 26. It can be seen from Fig. 25 that if the pounding of structures happens, the peak roof acceleration of Structure A increases sharply with increasing of shear wave velocity initially. The increase rate reduces after the wave velocity reaches 200 m/s. When the wave velocity approaches about 400 m/s, the peak acceleration response tends to a constant value. Different from the acceleration response, the displacement of Structure A decreases with increasing of shear wave velocity at the beginning, and then the decrease rate reduces gradually. When the wave velocity approaches about 400 m/s, the peak displacement response almost remains unchanged. The reason is that the pounding responses depend on the stiffness of pounding systems. The larger the shear wave velocity of soil is, the bigger stiffness the pounding system has. Hence the pounding acceleration responses increases and the displacement response decreases with increasing of system stiffness. When the wave velocity approaches 400 m/s, the foundation of structure is nearly fixed. Thus its stiffness contribution to the system is almost unchanged. We can also see from Fig. 25 that if no pounding happens between adjacent buildings, the variation trends of acceleration and displacement as the increasing of wave velocity are similar to those of pounding cases, but the range of variation is smaller than that of pounding case. This observation shows that the free vibration responses of structure are more sensitive to soil than pounding responses.

Fig. 26 shows that the variation trends of pounding responses for Structure B is similar to that for Structure A, but the range of variation is much larger. For example, the displacement factor of Structure B is about 0.81 at velocity of 50 m/s and 1.51 at velocity of 150 m/s, while that of Structure A is 0.86 at velocity of 50 m/s and 1.22 at velocity of 150 m/s. The variation range of Structure B is more than twice of Structure A. The reason is that the stiffness of Structure B is smaller than Structure A. Hence, Structure B is more sensitive to PSSI than Structure A.