Numerical study on bored Pile-Soil interaction by specified constitutive model in coastal engineering (design)

2.1. Material model demonstration

The ‘M-C constitutive model’ has linear elastic with perfect plastic characteristic, and commonly wide used in linear material, in this case, to have better fitting with practical scenario, author introduced a hardening soil model (HSs), which is an advance model to simulate various stiff and soft soil, the yield surface of ‘M-C’ model are fixed in principal stress space, on the contrary, the surface in the ‘HSs’ model is flexible, and the yield surface can expand due to plastic straining, models yield surfaces depicted in Fig. 2(a, b). The ‘HSs’ model is non-linear soil model under cyclic loading, which followed Masing's rule [9, 10], the hardening plasticity accounts for more rapidly decaying small-strain stiffness during initial loading, therefore, the mechanic features showing in Fig. 2(c).

For the Hardening soil model, the most important parameters are the plastic straining from primary deviatoric loading $E_{50}^{ref}$, and compression loading $E_{oed}^{ref}$, also with elastic unloading and reloading $E_{\mathrm{u}\mathrm{r}}^{ref}$ as the auxiliary parameters. As the advanced model, HSs model is restrained by initial shear modules $G_0$ and shear strain level ${\gamma }_{0.7}$ as well. In this article, the induction procedures of ‘HSs’ model formula are not the priority, we focus on the model performance, the demonstration of ‘HSs’ model can be referred from Alarcón et al. [5], Surarak et al. [7] and Brinkgreve et al. [13], the relevant parameters mentioned above in this case depend on their methodology.

Fig. 2a) Yield surface of ‘M-C model’, b) yield surface of ‘HSs model’, c) stiffness reduction in initial or primary loading and in unloading / reloading on Hardening Soil Model [3, 11, 12]

a)

b)

c)

2.2. Engineering case description

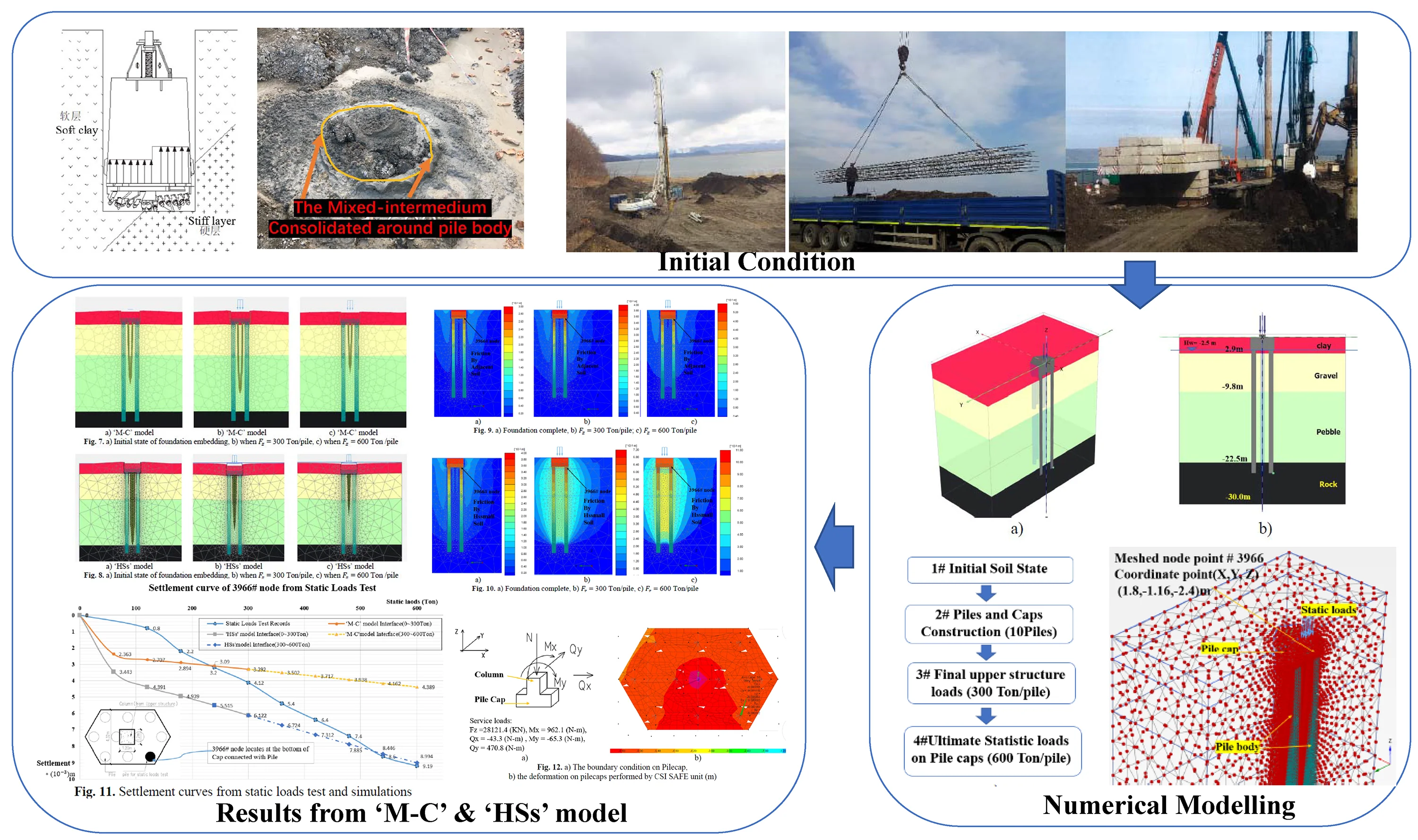
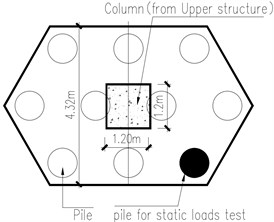
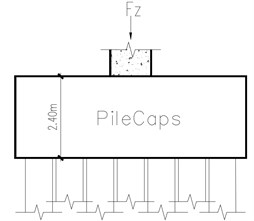
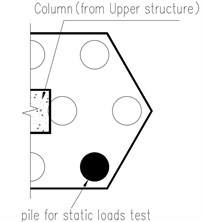
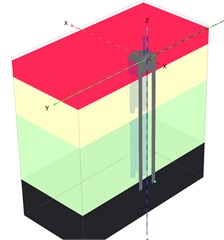
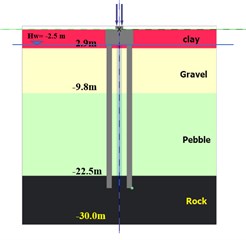
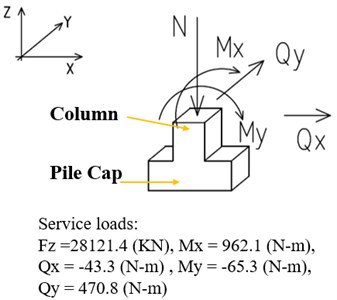
The structure building located in North-east Asian coastal area with constantly underground seawater level $H_w$ = –2.5 m, the upper structure is 12F concrete reinforcement building (RC) standing on the pile caps combined with Mat foundations, the vertical loads on the test pile cap from upper structure, $F_z$ = 28200 KN. The pile cap involved here has 10 piles ($D=$800 mm, $L=$ 22 m) underground, the pile cap structure details refer Fig. 3(a), (b), (c), all endings of piles are embedded in the ‘Rock’ strata more than 1m (refer the Fig. 4(a), (b)), which means, each pile should be capable of 300 Ton bearing capacity to support upper structure. As per structure design demands and following the static loads test code [14, 15], the ultimate bearing capacity should reach to 600 Ton for each pile.

Fig. 3a) Top view of pile cap, b) front view of pile cap, c) symmetrical top part of pile cap

a)

b)

c)

In the modeling phase, it is obvious that the pile cap is symmetrical structure Fig. 3(a), hence, author adopt symmetrical part showing in Fig. 3(c).

Fig. 4(c) is a simplified test and data collection procedure, in the practical phase, the static loads test would experience 10 magnitudes loads at least, as per test plan, the static loads in each step are 120 Ton, 180 Ton, 240 Ton …600 Ton respectively (each step loads increased by 60 Ton). When start doing numerical analysis, setting initial stresses for soil (K0 procedure), then setting service loads step by step till $F_z=$ 300 (Ton/pile) and the same loading periods followed the practical test scheme. The review of bore piles drilling, rebar cages installation and static loads tests showing in Fig. 5.

Fig. 4a) Perspective of modeling pile cap; b) stratigraphic profile; c) analysis procedure

a)

b)

c)

Fig. 5a) Bored pile drilling, b) installation of rebar cage, c) static loads test (Max 600 ton/pile)

a)

b)

c)

2.3. Material model parameters collection

According to the pile concrete compressive strength ${f\text{'}}_c$ test report and Geo-lab test, ${f\text{'}}_c=$ 25.6 MPa, $E_{50}^{ref}=\mathrm{}{E}_{oed}^{ref}=$ 20 KPa, $E_{\mathrm{u}\mathrm{r}}^{ref}=$ 60 KPa, initial shear modules $G_0=$ 26 MPa. Thus, the complete parameters tables showing in Table 1.

3.1. Demonstration of modeling and numerical analysis procedure

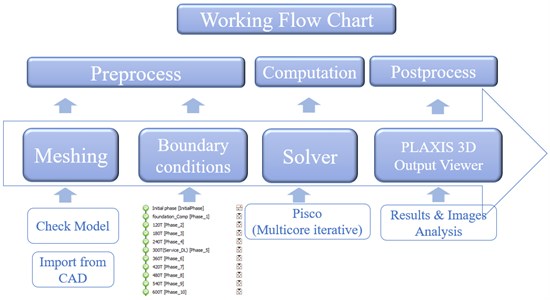
During the finite element analysis procedure, author established the pile-cap with soil models in Space-Claim, and pile caps and pile bodies are built by solid model with concrete material, the strata information from Table 1, addressed the soil materials properties, the numerical study and analysis procedures depicted in Fig. 6 series.

Fig. 6a) The basic workflow on the numerical analysis, the boundary conditions are described in Fig.12 where can be used for structure design and understood easily as well, b) the pile cap solid model in symmetrical form, c) the meshed node # 3966 track for post processing, d) the practical test position matched the model mesh location

a)

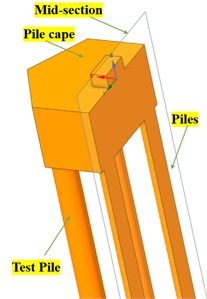
b)

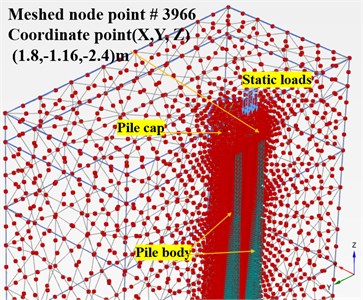
c)

d)

3.2. Deformation results post processing

Extracting the deformation results from meshed model in PLAXIS, and captured main results in Fig. 7.

From Fig. 7 and Fig. 8, when adopting ‘M-C’ and ‘HSs’ model, it is obvious that there are huge disparities on the deformation of soil among piles in mesh. In terms of deformation time order and consequent, ‘HSs’ model performed much more reasonable: when drilling commenced, pile and caps broke the equilibrium of soil initial stress and soil deformation reached the maximum swell after the bore piles and pile caps construction (cycle loads from equipment during all drilling process), when upper loads reached service design loads ($F_z$= 300 Ton/pile), the soil initial consolidation complete and the medium soil stress around pile body gradually keep equilibrium with surrounding soil. Due to the pile body already embedded into the rock strata and soils consolidated, when ultimate loads ($F_z$= 600 Ton/pile) worked, the soil deformation had similar performance like the service loads ($F_z$= 300 Ton/pile) did.

Fig. 7a) Initial state of foundation embedding, b) when Fz = 300 Ton/pile, c) when Fz = 600 Ton /pile

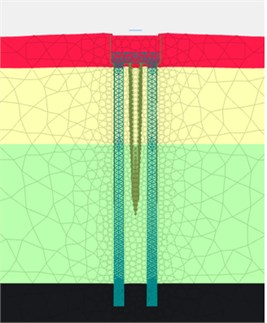
a) ‘M-C’ model

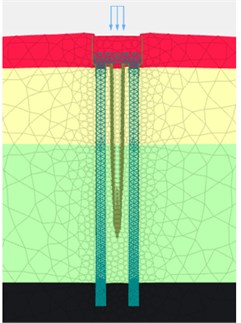
b) ‘M-C’ model

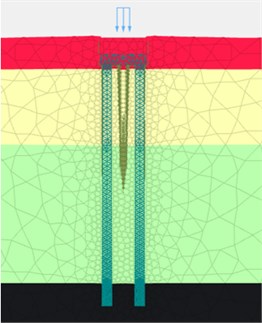
c) ‘M-C’ model

Fig. 8a) Initial state of foundation embedding, b) when Fz = 300 Ton/pile, c) when Fz = 600 Ton /pile

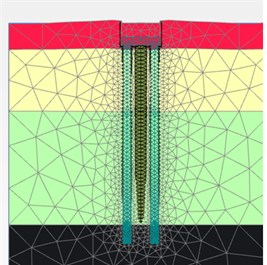
a) ‘HSs’ model

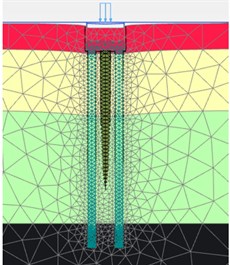
b) ‘HSs’ model

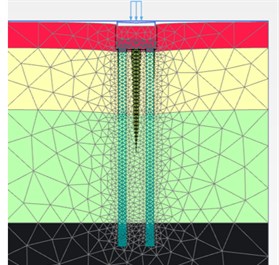
c) ‘HSs’ model

3.3. The settlement results post process

The numerical simulation of settlement on piles can be described in Fig. 9 and Fig. 10.

Selecting the typical node (#3966) which marked in Fig. 6(c, d) and Fig. 9 and Fig. 10, established the settlement curves chart in Fig. 11. In terms of pile settlement, during the static loads test procedure, when loads on mono plie commenced from initial self-weight to ultimate loads ($F_z$ = 600 Ton/pile), the settlement by ‘M-C’ model as the interface medium whose frictions controlled by adjacent soil and reduction coefficient $R$ ($R=$0.7-0.9), performed smaller quantities than the practical test results, to be more precisely, when reached service and the ultimate loads ($F_z$= 300 and 600 Ton/pile), the settlements $U_{z(M-C)}=$ –3.29×10^-3 m and –4.39×10^-3 m, these values are much lower than practical test ($U_{z\left(test\right)}=$ –4.12×10^-3 m and –9.19×10^-3 m). On the other side, the ‘HSs’ models showed a similar settlement trend and displacement quantities approached the practical static loads test results, when reached the service loads ($F_z$= 300 Ton/pile), the $U_{z\left(HSs\right)}$ = –6.12×10^-3 m, the smooth curve connected with previous checkpoint performed similar trend like practical test curve, when reached the ultimate loads ($F_z$ = 600 Ton/pile), the $U_{z\left(HSs\right)}$ = –8.99×10^-3 m, nearly equal to $U_{z\left(test\right)}=$ 9.19×10^-3 m.

In the practical situation, with the restrain of upper structure loads, most piles will resist service loads ($F_z$= 300 Ton/pile) in their life cycle, the scenarios that suffering the ultimate load ($F_z$= 600 Ton/pile), are mostly possible appeared in the static loads test only, therefore, the ultimate loads ($F_z$= 600 Ton/pile) phrase can be predicted by numerical simulation, the dash line (yellow and blue) are the simulation results from settlement predictions.

Fig. 9a) Foundation complete, b) Fz = 300 Ton/pile; c) Fz = 600 Ton/pile

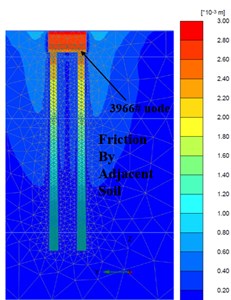
a)

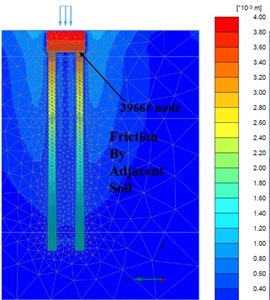
b)

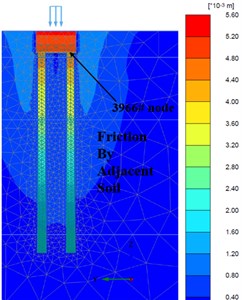
c)

Fig. 10a) Foundation complete, b) Fz = 300 Ton/pile, c) Fz = 600 Ton/pile

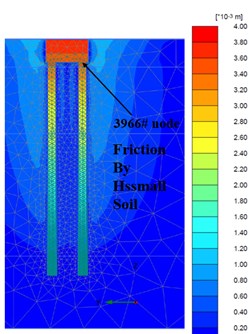
a)

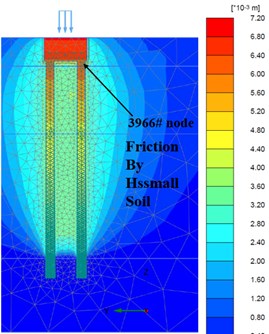
b)

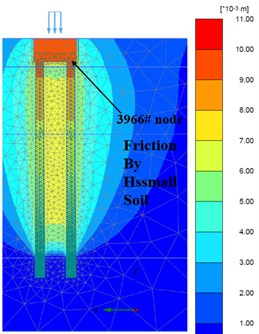
c)

Fig. 11Settlement curves from static loads test and simulations

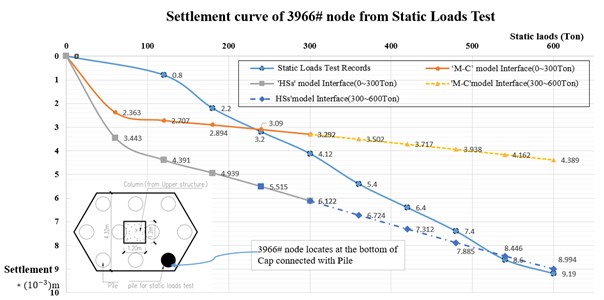
To cross verify the results, it is necessary to build numerical model in CSI SAFE with the same parameters, and illustrate the boundary conditions in Fig. 12(a), then record the final settlement result images in Fig. 12(b), focus the same test location, it is clear that when the service loads on the pile cap ($F_z$= 300 Ton/pile), the maximum settlement of pile $U_z$ = –6.36×10^-3 m, nearly match the ‘HSs model’ results at the same load magnitude in Fig. 11.

Fig. 12a) The boundary condition on Pilecap, b) the deformation on pilecaps performed by CSI SAFE unit (m)

a)

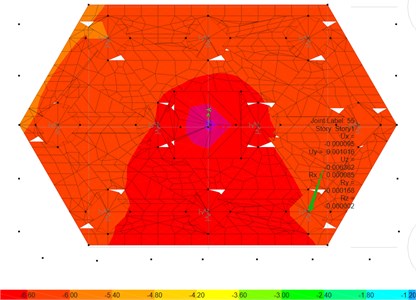
b)