Calculation of earth pressure on rigid retaining walls with considerations to the seismic load and soil stress-deflection

1. Introduction

Due to frequent earthquakes that have happened recently, retaining wall failures caused by earthquake occur occasionally. Seismic load is an accidental loading. Whether the seismic load and its point of action can be calculated accurately has become extremely important to the seismic design of retaining walls. At present stage, the quasi-static and quasi-dynamic methods are two major approaches used to calculate earthquake-induced earth pressure of rigid retaining walls. The quasi-static method follows a simple principle and can be easily operated; thus, it is used frequently. The most typical quasi-static method is the Mononobe-Okabe(M-O) formula, which was established by Japanese scholars Mononobe [1] and Okabe [2] on the basis of the limit equilibrium theory. Under seismic loading, active earth pressure behind a retaining wall has a linear distribution, and the point of resultant action is one-third of the wall height above ground. This finding disagrees with the experimental result of Sherif [3] and Ishibashi [4], in which active earth pressure behind the retaining wall has a nonlinear distribution. Later, Choudhury and Singh [5], Saran and Gupta [6], Shukla et al. [7], Ghosh [8], Sharma and Ghosh [9], Lin et al. [10] improved the M-O formula and reported the calculation formula of nonlinear distributed active earth pressure under seismic loading. However, these formulas did not consider the active earth stress-deflection after the retaining wall. According to the mobile gate test of Terzaghi [11] and several theoretical studies (Handy [12]; Paik and Salgado [13]; Rao et al [14] and Cai [15]), stress-deflection in soil is objective. Zhou [16], Anindya [17] discussed effects of soil stress-deflection on earth pressure under seismic loading. These research methods were based on the hypothesis that the fracture surface is a surface running through the wall heel under seismic loading. However, Zhu [18] discovered in the laboratory test of earth pressure on the gravity retaining wall that the upper deflection of the retaining wall grows quickly, while lower deflection was relatively slight. Nevertheless, there are few studies on earthquake-induced active earth pressure based on the changing angle of rupture. Ellis [19] analyzed nonlinear distribution of the active earth pressure by viewing the fracture surface as a curved one. However, this hypothesized curved surface used cycloid under non-seismic loading as the fracture surface model, thus failing to reflect effects of seismic loading truly.

In this paper, to address the aforementioned issues, a novel approach for calculating the active earth pressure on rigid retaining walls with considerations to the seismic load and soil stress-deflection was proposed. Firstly, a balance equation was constructed by the principle of zero horizontal resultant force. As such, the calculation formula of soil angle of rupture which changes with wall height was established. Then, calculation formulas of the active earth pressure, the seismic active earth force, the total moment at the wall and the point of application of active thrust from the base of wall were constructed. The predictions of the proposed method were verified against results of other previously published methods.

2. Deduction of formula

For the purpose of simplification in this analysis, the following assumptions are made:

1) Influences of angle difference between ${\alpha }_s$ and ${\alpha }_w$ are neglected when calculating the arc radius of soil stress-deflection ($R$). Where ${\alpha }_s$ and ${\alpha }_w$ represent the rotation angle of the principal stress on the differential flat element on the active sliding surface and the deflection angle of major principal stress at wall respectively.

2) Vertical soil stress is approximately $\gamma y$.

The mechanical model of micro-smooth crack is shown in Fig. 1. When seismic load is neglected, the shear stress on the thin layer can be expressed as:

Since there’s no shear stress was observed on the horizontal layer, there’s:

By integrating Eq. (3) with respect to $L$. It can get:

According to the assumption:

Substituting these into Eq. (7), it can be rewritten as:

If the retaining wall is divided into $N$, and at the depth of $y=n\mathrm{\Delta }H$, then:

Seismic angle of rupture can be expressed as:

According to this formula, the angle of rupture changes in a curve manner from the upper to bottom parts of the retaining wall. A small angle of rupture is observed at the upper positions, and a large angle at lower positions. With respect to failure mode, large failure area is observed at upper positions, but small failure area at lower positions, which is consistent with experimental results. If neither seismic load nor stress-deflection is considered, the angle of rupture is degraded to the angle of rupture of Rankine earth pressure.

Fig. 1The force model of the slip crack body

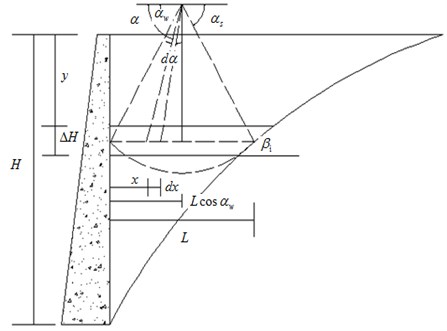
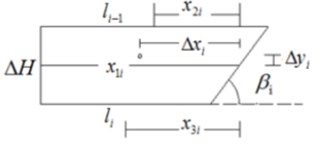
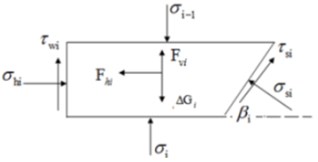
Fig. 2The size and stress analysis of layer I

a)

b)

The stress of the thin layer is analyzed. Component sizes and stresses are shown in Fig. 2. Based on sectional geometric calculation of soil layers, it gets:

The force and moment equilibrium equation of lay $i$ is presented:

The following relations should be satisfied when soil stress-deflection:

Above all kinds of simultaneous, it gets:

where:

Hence, the seismic active earth force ($E_a$), the total moment at the wall ($M$), the point of application of active thrust from the base of wall ($y_0$) can be calculated as follows:

Effects of soil stress-deflection and seismic loading are considered comprehensively in this formula. Earth pressure is in nonlinear distribution along wall height. If neither seismic load nor stress-deflection is considered, the formula becomes the formula of Rankine earth pressure.

3. Validation

3.1. Comparison with test data and other methods

To verify the rationality of the proposed method, calculated results were compared with the test data in References obtained by sensor networks [20] and results of other calculation methods. The results are listed in Table 1, where $P_a$ is the maximum active earth pressure and $E_a$ is the seismic active earth force. As shown in Table 1, the proposed method obtains the closest results with the test data than other methods. Among the test data, $E_a$ was a mean when $k_h=$ 0. The maximum test value of $E_a$ was 557 N, whereas the calculated result of the proposed method was 580 N. Hence, the calculated results of the proposed method best match with test data.

Table 1Comparison with other methods

	Test data		Proposed method		Zhou [16]		Mononobe-Okabe
$k_h$	$P_a$ (kPa)	$E_a$ (N)	$P_a$ (kPa)	$E_a$ (N)	$P_a$ (kPa)	$E_a$ (N)	$P_a$ (kPa)	$E_a$ (N)
0	1360	406	1417	580	1513	633	2080	646
0.3	2030	750	1496	744	2995	866	3670	991

Fig. 3The seismic wave’s data and structure calculation model

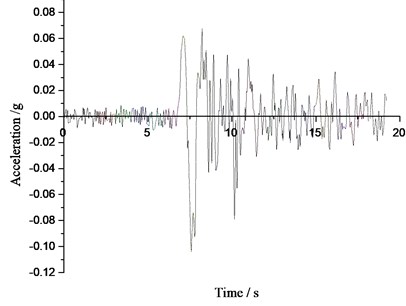
a) Acceleration time-history curve of Tianjin earthquake

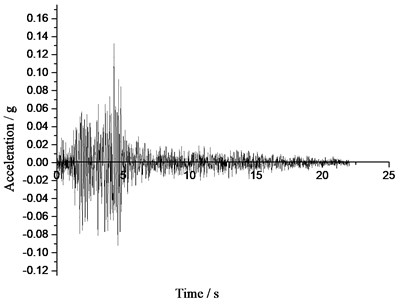
b) Acceleration time-history curve of Tangshan earthquake

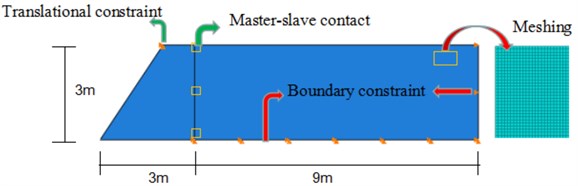
c) The model of structure calculation

3.3. Comparison with FEM’s result

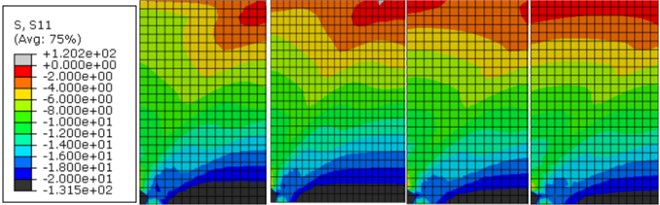
The whole analysis was accomplished in two steps, the dead weight of soil mass was initially added, and then seismic load was applied. The results are shown in Fig. 4, 5. The distribution clouds of active earth pressure of different models and earthquakes behind the retaining wall are shown in Fig. 4. In order to see the distribution of active earth pressure more directly, the active earth pressure behind retaining walls of different models and earthquakes was extracted by setting path, and then compared with calculated results which are shown in Fig. 5.

From the Fig. 5, we can find the active earth pressure behind the retaining wall is in nonlinear distribution easily. Fig. 4, 5 illustrates that no matter what plasticity model is used, the distribution of pressure is in nonlinear. According to Fig. 5 the result of Mohr-Coulomb plasticity model is better than Drucker-Prager. In addition, the parameters in the model of Mohr-Coulomb are less than Drucker-Prager, and the parameters need to be converted in the latter model. To avoid the adverse impact of parameter values on the results, the former plasticity model was adopted in the following discussion.

Fig. 4Stress cloud of soil active earth pressure behind the wall

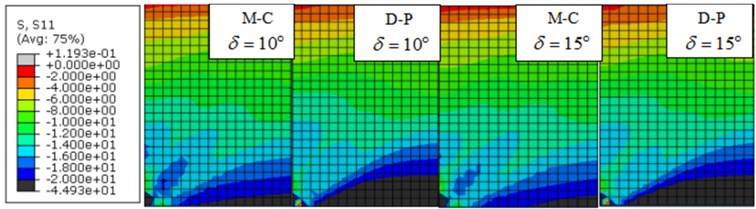
a) Tianjin earthquake

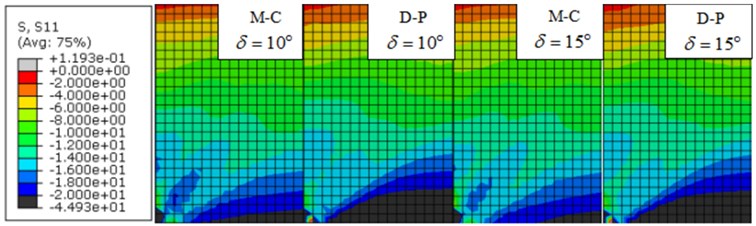
b) Tangshan earthquake

Fig. 5Active earth pressure distribution along the height of the rigid wall

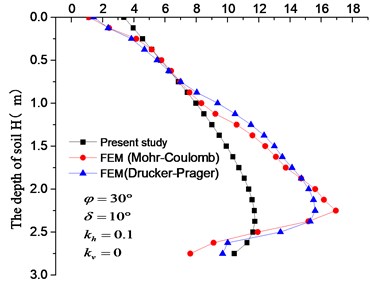
a) Tianjin earthquake

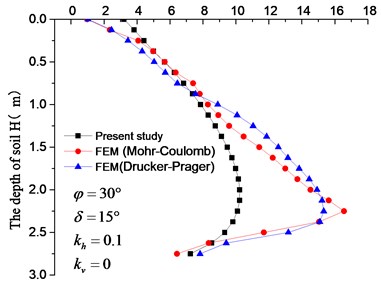
b) Tianjin earthquake

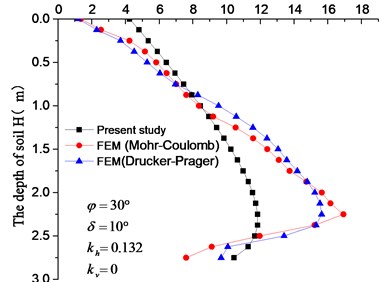
c) Tangshan earthquake

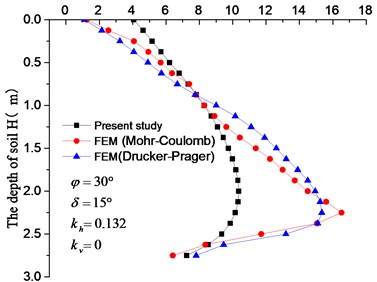
d) Tangshan earthquake

4. Discussion

The influence of each parameter is discussed in this part. Due to the quasi-static method (M-O formula; Zhou [16]; Sharma and Ghosh, et al. [9]) consider the peak value of the earthquake only, and in order to avoid the limitation of a real earthquake which represents a particular place at a particular time, the waveform is not to be considered here. The discussion results are listed as follows.

4.1. Distribution of earthquake-induced active earth pressure

Earth pressure distributions behind the retaining wall with considerations to the combined effect of seismic loading and soil stress-deflection are shown in Figs. 6-11. The retaining wall height was $H=$ 3 m, soil friction angle $\phi =$ 30°, wall-soil interface friction angle $\delta =$ 10°, unit weight of the backfill soil $r=$ 17 kN/m³and the surface load $q=$ 0. In Fig. 6, earth pressure behind the retaining wall was in a nonlinear distribution under the combined effect of seismic loading and soil stress-deflection. With the increase of horizontal seismic coefficient $k_h$, the upper active earth pressure soars up, while the lower active earth pressure increases slightly (and even remains same), thus resulting in a quick upper deformation and small lower deformation. This result conforms to the test results of the reference and the finite element simulation stress cloud in Fig. 7.

Fig. 6Effect of kh on active earth pressure distribution along the height of the rigid wall

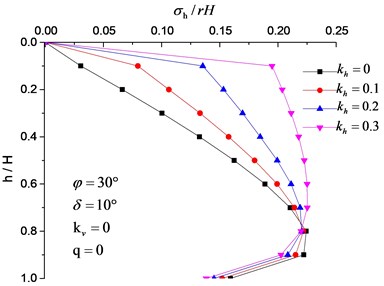
Fig. 7Active earth pressure cloud of different kh

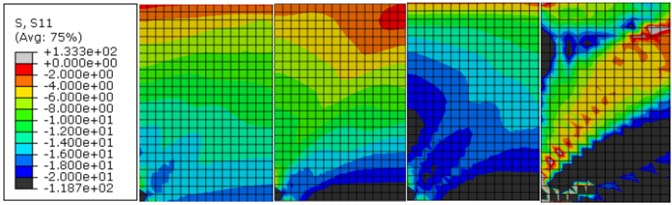
Fig. 8 present that the active earth pressure under seismic loading is negatively correlated with internal friction angle. The active earth pressure distribution cloud under different soil friction angle is shown in Fig. 9. The comparison of the colors of the corresponding nodes and figures concludes that earth pressure gradually decreases with the increase of internal friction angle.

Fig. 8Effect of φ on active earth pressure distribution along the height of the rigid wall

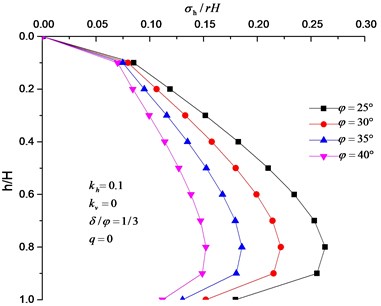
Fig. 9Active earth pressure cloud of different φ

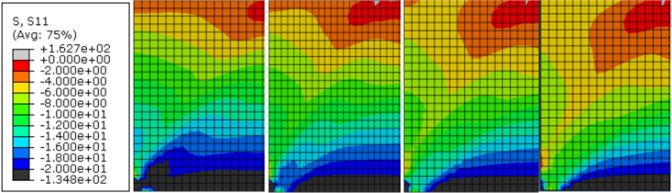
Fig. 10Effect of δ on active earth pressure distribution along the height of the rigid wall

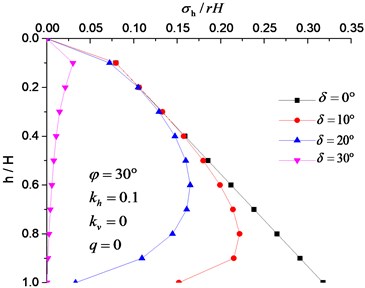
Fig. 11Active earth pressure cloud of different δ

It can be seen from Fig. 10, 11 that the active earth pressure under seismic loading decreases with the increase of $\delta$. Moreover, the active earth pressure behind the retaining wall has a straight distribution when $\delta$ = 0, which is consistent with the M-O theory. When $\delta$ approaches to $\varphi$, the active earth pressure tends to be 0, which evidently disagree with practical situations and the results presented in Fig. 11(d). This finding also demonstrates that this formula is inapplicable to the situation when $\delta$ approaches to $\varphi$.

4.3. Analysis on influencing factors of the coefficient of seismic active earth pressure

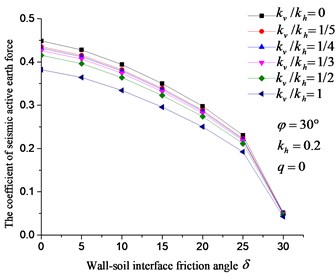
The concept of earth pressure coefficient in soil mechanics was used. In this work, the earth pressure coefficient was defined as the ratio between seismic active earth force and 1/2 $\gamma H^2$. In Fig. 14, 15, earth pressure coefficient increases with the increase of $k_h$, but decreases with the increase of $\phi$, $\delta$ and the vertical seismic coefficient ($k_v$). Data in Fig. 14, 15 also reflect that the minimum change amplitude of earth pressure coefficient with $\phi$, $\delta$, $k_h$ is 28 %, 48 %, 49 % respectively. When $k_v/k_h$ increases from 0 to 1, the maximum reduction of earth pressure coefficient is 17 %, implying that $k_v$ is less important to earth pressure coefficient more than other factors.

Fig. 12Effect of φ, q on the relative height of point of active earth force

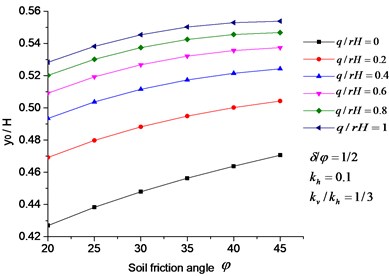
Fig. 13Effect of kh, δ on the relative height of point of active earth force

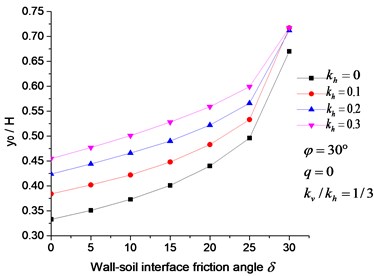
Fig. 14Effect of kh, φ on the coefficient of seismic active earth pressure

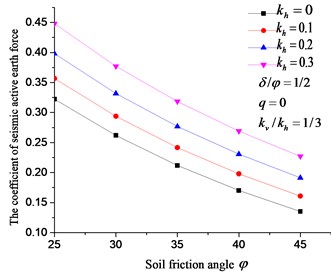
Fig. 15Effect of kv, δ on the coefficient of seismic active earth pressure

4.4. Analysis on influencing factors of seismic active earth force

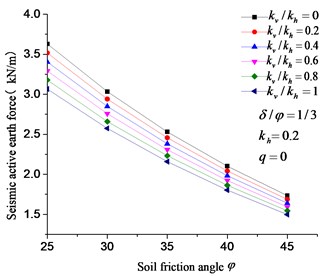
As shown in Fig. 16-17, the earthquake-induced seismic active earth force is positively related with $k_h$, but negatively correlated with $\phi$, $\delta$ and $k_v$. Similarly, Fig. 17 shows that $k_v$ is less important to resultant active earth pressure compared with other influencing factors, which slightly influences earth pressure. This finding agrees with the analysis results in Fig. 4.

Fig. 16Effect of kh, δ on the seismic active earth force

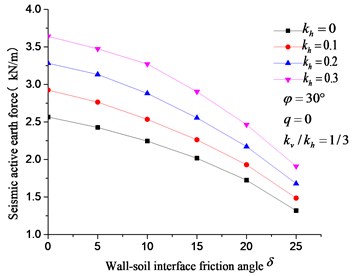
Fig. 17Effect of kv, φ on the seismic active earth force

5. Conclusions

1) Stresses on soil layers of the vertical retaining wall under seismic loading were analyzed by quasi-static method with considerations to soil stress-deflection. The calculation formula of the active seismic angle of rupture which changes in the retaining wall height was deduced, thus obtaining a seismic active earth pressure, seismic active earth force, the total moment at the wall and point of application of active thrust from the base of wall. The calculated results of the proposed method were compared with the test data and finite element simulation results, verifying the high efficiency of the proposed method. In addition, this method can be used to fill different properties.

2) In this study, the effects of $\phi$, $q$, $k_h$, $k_v$, $\delta$ and other factors on height of point of resultant pressure, earth pressure coefficient and earthquake-induced active earth pressure were discussed. The result finds that $k_v$ is less important to earth pressure coefficient compared with other parameters.

3) The calculated results based on the changing seismic angle of rupture agree basically agree with the test data and ABAQUS finite element simulation result, and are closer to the measured values compared with other theories. Therefore, the proposed method is reliable and can provide references for actual engineering.