Abstract
In order to detect the damages in rubber-bearing isolated structures, a rubber-bearing isolated building model was established and tested on shake table experimentally in the laboratory. Different earthquakes were used to drive the shake table and the stiffness element device (SED) was adopted herein to reduce the stiffness of the upper story of the model abruptly to simulate structural damages during the test. The adaptive extended Kalman filter (AEKF) approach is proposed to identify the parameters and track the parametric variation of rubber-bearing isolated structure online and to identify the displacements of every story using the measured acceleration responses. The identification results of the experiments demonstrate that the AEKF approach is capable of identifying the parameters of rubber-bearing isolated structure accurately and tracking the parametric variations of the structure effectively, leading to the detection of structural damages, including the damage locations and severity. And the predicted displacements also match well with the experimental data, indicating the effectiveness and accuracy of the proposed AEKF approach in detecting the damages in rubber-bearing isolated structures with practical application value.
1. Introduction
The base isolation is an innovative technique to mitigate earthquake damage potential and thus has widely applications now, especially the high damping rubber-bearing isolation systems which have been used in buildings and bridges and will become more popular in the future due to their ability to reduce significantly the structural responses subject to earthquakes and other dynamic loads [1-2]. To ensure the integrity and safety of these rubber-bearing isolators and the corresponding base-isolated structures, a structural health monitoring system should be developed. To accomplish this effort, two important tasks should be settled firstly. One is the modeling of the rubber-bearing isolators, i.e. a suitable model should be established to describe the nonlinear hysteretic character of the rubber-bearings, and the other is the effective damage detection technique for these rubber-bearing isolated structures.
Different hysteretic models have been proposed in the literature, including the bi-linear model [3], tri-linear model [4], Bouc-Wen model [5, 6], etc. Among these models, the Bouc-Wen model involves moderate amount of parameters to be adjusted and has better flexibility with wide application. Hence the Bouc-Wen model is adopted in this paper to describe the hysteretic behavior of the rubber-bearing isolation system.
The ability to assess the state of the structure, including its damages immediately after a severe event, will allow a rapid assessment of the civil infrastructures for the post-event emergency response, rescues and management, to guarantee the safety operations of these structures. Hence intensive research has been conducted for detecting structural damages based on vibration data measured from sensors. Various approaches have been proposed in the literature, such as the least-square estimation (LSE) [7-9], the extended Kalman filter (EKF) [10, 11], the unscented Kalman filter (UKF) [12, 13], the sequential non-linear least-square estimation (SNLSE) [14], quadratic sum-squares error (QSSE) [15], wavelet multiresolution technique [16], probabilistic approach [17], and others [e.g. 18-20]. Among these techniques mentioned above, an adaptive tracking technique based on the EKF approach has been proposed for tracking the time-varying parameters on-line [10, 11]. Simulation results demonstrate that this adaptive EKF approach (AEKF) is capable of tracking the variations of structural parameters, such as the degradation of stiffness due to structural damages.
In this paper experimental studies are performed and presented to verify the capability of the AEKF approach for identifying and tracking damages in nonlinear structures. The Bouc-Wen model is selected to describe the non-linear behavior of rubber-bearings, which has the advantages of being smooth-varying and physically motivated. Further, experimental tests using a base-isolated building model, consisting of a scaled shear-beam type building model mounted on a rubber-bearing isolation system using a particular type of rubber-bearing (GZN110), have been tested experimentally in the laboratory. To simulate structural damages during the test, the stiffness element device (SED) [11] is proposed herein to reduce the stiffness of the model abruptly. Different earthquake excitations have been used to drive the shake table, including the El Centro earthquake and Kobe earthquake. Various damage scenarios have been simulated and tested. Measured acceleration data and the AEKF approach are used to track the variation of stiffness during the test. Experimental results demonstrate that the Bouc-Wen model is capable of describing the non-linear behavior of rubber-bearings and that the AEKF approach is capable of tracking the variation of hysteretic structural parameters leading to the detection of structural damages.
2. On-line damage identification of rubber-bearing isolated building
In order to describe the nonlinear hysteretic behavior of the rubber-bearing isolation system, an analytical model should be established. Different hysteretic models have been proposed in the literature, among which the Bouc-Wen model involves moderate amount of parameters to be adjusted and is more suitable for the rubber-bearing isolation system [5, 6]. Hence the Bouc-Wen model is adopted in this paper to model the dynamic character of the isolation system. And a brief summary of on-line damage identification of rubber-bearing isolated building using the adaptive extended Kalman filter (AEKF) approach is given as follows.
Consider a 2-DOF rubber-bearing isolated structure consisting of an upper storey and a base-isolation storey excited by a ground acceleration . The equation of motion can be expressed as:
where and , and , and are the mass, damping and stiffness coefficients of the base-isolation storey and upper storey, respectively. and are the relative acceleration responses of the base-isolation storey and upper storey, respectively. is a hysteretic variable, , , and are the hysteretic parameters in the Bouc-Wen model. Yin et al. [5, 6] suggested that 0.5, 0.5, 2 for rubber bearings, these parameters are adopted in this paper for reference and the following experimental results are compared with these suggested values.
For the EKF approach an extended state vector is introduced, where
and represent the displacement vector and the velocity vector,
is an n-unknown parametric vector with ( 1, 2, …, ) being the ith unknown parameter of the structure, including damping, stiffness and hysteretic parameters. Then the vector equation of motion of the structure can be expressed as:
in which is the model noise (uncertainty) vector with zero mean and a covariance matrix , and is the excitation vector. A nonlinear discrete vector equation for an observation vector (measured responses) can be expressed as follows:
in which is a -dimensional observation (measured) vector at ( is the sampling time step), i.e. and . In Eq. (3) is a measurement noise vector assumed to be a Gaussian white noise vector with zero mean and a covariance matrix where is the Kroneker delta.
Let be the estimate of at and be the estimate of at . The recursive solution of the extended Kalman filter for the estimate is given as follows:
where is the transition matrix of the extended state vector from to . The EKF approach above can be used to identify the constant structural parameters. In order to track the parametric changes due to the damages, an adaptive factor matrix is presented to adjust the error covariance matrix , i.e.:
By replacing the in Eqs. (6) and (7) using Eq. (10), the recursive solution for adaptive EKF approach (AEKF) is thus obtained to track the time-varying structural parameters. The determination of has been described in [10]. The initial values for the unknown extended state vector should be estimated. Likewise the initial error covariance matrix of the estimated extended state vector, the covariance matrix of the measurement noise vector and the covariance matrix of the system noise vector should be also assigned. Finally, in computing the adaptive factor matrix for the on-line damage identification, a constrained optimization procedure was used, in which a small number (constraint) 0.01 was suggested. Further, in computing the covariance matrix of the predicted output error, it was suggested in [10] that 0, 0. These values will be used in the following for the analysis of all experimental data.
3. Experimental set-up
A base-isolated building model, consisting of a 400 mm by 300 mm small-scale shear-beam type building model mounted on a 600 mm by 500 mm rubber-bearing isolation system, as shown in Fig. 1, is used for the experiments. The total height of this building model is 660 mm, the height of upper story is 345 mm and the height of the isolation storey is 315 mm. The total weight of the model is 350 kg and the mass of upper floor is 50 kg, the mass of the nether floor is 300 kg. The first two natural frequencies of the test specimen are 1.955 Hz and 5.376 Hz, respectively. Based on the discretized 2-DOF shear-beam model, the stiffness of each story are obtained as 52 kN/m and 46 kN/m, respectively, using the finite-element approach.
The base-isolated building model was placed on the shake table that simulates different kinds of earthquakes. Two earthquake excitations were used, including the El Centro and the Kobe earthquakes. During the tests the shake table and the masses were each installed with one acceleration sensor and one displacement sensor to measure the responses. The absolute acceleration responses of the isolation storey and of the upper storey , as well as the earthquake acceleration were measured. Also the displacements of each storey and the base were measured for the correlation study.
The damage in a story unit is assumed to be reflected by the reduction of its stiffness. To simulate the reduction of stiffness in the upper story, a stiffness element device (SED), consisting of a hydraulic cylinder-piston (HCP) and a bracing system, with an effective stiffness of is installed in the upper storey, so that stiffness of the upper storey is increased by . During the experimental test, the effective stiffness of the SED is reduced to zero to simulate the reduction of the stiffness in the upper storey.
Fig. 1The rubber-bearing isolated building model on the shake table

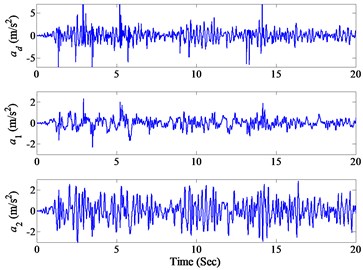
Fig. 2Measured accelerations under El Centro earthquake excitation
4. Experimental results
To demonstrate the capability and accuracy of the adaptive extended Kalman filter (AEKF) approach for tracking the damage of base-isolated structures, experimental tests are conducted herein for different damage scenarios. For shake table tests two earthquakes will be used, including the El Centro earthquake scaled to a peak ground acceleration (PGA) of 0.6 g and the Kobe earthquake scaled to a PGA of 0.5 g. For each earthquake the acceleration responses of both floors and the shake table acceleration were measured. Further the displacement responses of both floors and the base were also measured for correlation studies later. The sampling frequency of all measurements is 500 Hz.
To identify the parameters of the rubber-bearing isolated structure and to track the damage in the upper storey when it occurs, Bouc-Wen model with different unknown parameters will be considered, i.e.:
(i) Model I: the Bouc-Wen model contains three known hysteretic parameters, i.e. 2, , and unknown;
(ii) Model II: the suggested values are adopted for the hysteretic parameters in Bouc-Wen model, i.e. 2, 0.5, 0.5, only with unknown.
And for both models above the following experimental scenarios were tested:
(a) The shake table was driven by El Centro earthquake. The cylinder of the SED was filled by air with an air pressure of 0.7 MPa. From the experimental test an air pressure at 0.7 MPa results in an effective stiffness of 7 kN/m for the SED, i.e. 7 kN/m. Thus the stiffness of the upper storey was estimated to be 46 kN/m + 7 kN/m 53 kN/m, whereas the stiffness of base-isolation storey was estimated to be 52 kN/m. During the test with the El Centro earthquake excitation, both valves of the SED unit were open simultaneously at 14 second, so that the stiffness of the upper storey reduced abruptly from 53 kN/m to 46 kN/m at 14 second.
(b) Instead of the El Centro earthquake, the Kobe earthquake was used to drive the shake table. The test configuration is similar to that of Scenario (a) presented previously, except that the air pressure of the SED installed in the first storey is 0.75 MPa. This results in a stiffness of 7.5 kN/m for the SED. Hence the stiffness of the upper storey prior to a damage is 46 kN/m + 7.5 kN/m 53.5 kN/m, whereas the stiffness of the base-isolation storey remains the same, i.e. 52 kN/m. During the test valves of the SED were open at about 8 second, following the most intensive portion of the earthquake, at that time k2 is reduced to 46 kN/m.
In this paper the damage tracking results are presented, taking the Model I subject to El Centro earthquake for example. For the AEKF approach, the test specimen is considered as a 2-DOF shear-beam building model and the equations of motion can be written, in which the stiffness and damping of each storey as well as the nonlinear hysteretic parameters of the base-isolation are unknown parameters. Consequently the vector equation of motion for the extended state vector can be established analytically. With the measured shake table acceleration and acceleration responses shown in Fig. 2, the unknown structural parameters, i.e. , ( 1, 2), , and can be identified on-line using the recursive solution of the AEKF approach.
For the AEKF recursive solution described previously, the following initial values are assumed: (i) the initial values for , , , and are: 40 kN/m, 0.1 kNs/m ( 1, 2), 0.5, 0.5, 0.5, (ii) the initial values for the displacements and velocities are zero, i.e. , , (iii) the initial error covariance matrix of the extended state vector is a diagonal matrix with the first 5 diagonal elements being 1 and the last 7 diagonal elements being 1000, and (iv) the covariance matrices of the measurement noise vector and the system noise vector are chosen to be and , respectively, where is a unit matrix.
Based on the AEKF recursive solution and the measured data, the identified unknown parameters for both stories are presented in Fig. 3 as solid curves (blue color). Also shown in Fig. 3 as dashed curves (red color) for comparison are the estimated results based on the finite-element method. Further, the identified inter-storey drifts and displacements of each floor using the AEKF approach are presented in Fig. 4 as solid curves (blue color), whereas the dashed curves (red color) are the measured experimental results for comparison. The identified numerical results based on the AEKF approach are as follows: (i) prior to damage 51.7 kN/m and 55.2 kN/m, and (ii) after damage 51.7 kN/m and 48.5 kN/m. It is observed from both Fig. 3 (solid curves) and the numerical results above that the identified structural parameters based on the AEKF approach are very reasonable in comparison with that estimated by the finite element method (dashed curves). The difference between the solid and dashed curves has been expected due to the structural uncertainty of the test model, including the shear-beam assumption. Figs. 3 and 4 clearly demonstrate that the AEKF approach is capable of tracking the variation of stiffness parameters, leading to the detection of structural damages.
The damage identification results using the presented AEKF method for all the scenarios tested experimentally in the laboratory are listed in Table 1, in which the reference values of the unknown parameters are also listed for comparison. It can be seen from Table 1 that the identified parameters of the isolated structure are about the same for both Bouc-Wen Model I and Bouc-Wen Model II under El Centro and Kobe earthquake excitations. The identified stiffness values for both stories are close to the reference values predicted by the FEM method with a maximum error of 6 % for the upper story, and the differences between the identified values and the reference values of the undamaged structural parameters are almost the same as with that of the damaged structural parameters. Such discrepancies have been expected due to the structural uncertainty of the test model caused by the strong nonlinear hysteretic character of the rubber-bearing isolation system.
Fig. 3The identified model parameters under El Centro earthquake excitation
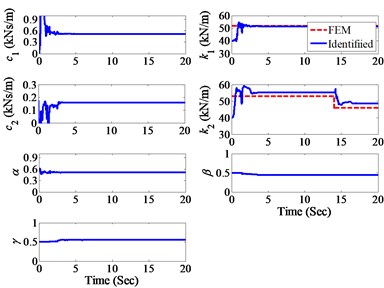
Fig. 4The identified drifts and displacements under El Centro earthquake excitation
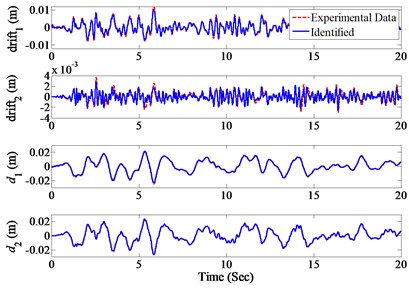
Table 1The identified parameters for Model I and Model II under different earthquakes
Parameters | (kNs/m) | (kNs/m) | (kN/m) | (kN/m) | |||||
El Centro earthquake | Prior to damage | Ref. value | – | – | 52 | 53 | – | 0.5 | 0.5 |
Model I | 0.52 | 0.16 | 51.7 | 55.2 | 0.51 | 0.46 | 0.54 | ||
Model II | 0.52 | 0.16 | 51.7 | 55.2 | 0.51 | – | – | ||
After damage | Ref. value | – | – | 52 | 46 | – | 0.5 | 0.5 | |
Model I | 0.52 | 0.16 | 51.7 | 48.7 | 0.51 | 0.46 | 0.54 | ||
Model II | 0.52 | 0.16 | 51.7 | 48.5 | 0.51 | – | – | ||
Kobe earthquake | Prior to damage | Ref. value | – | – | 52 | 53.5 | – | 0.5 | 0.5 |
Model I | 0.49 | 0.16 | 52.2 | 55.7 | 0.55 | 0.5 | 0.5 | ||
Model II | 0.49 | 0.16 | 52.2 | 55.6 | 0.55 | – | – | ||
After damage | Ref. value | – | – | 52 | 46 | – | 0.5 | 0.5 | |
Model I | 0.49 | 0.16 | 52.2 | 48.6 | 0.55 | 0.5 | 0.5 | ||
Model II | 0.49 | 0.16 | 52.2 | 48.5 | 0.55 | – | – | ||
5. Conclusions
Experimental studies have been performed in this paper to verify the capability of this adaptive extended Kalman filter (AEKF) in identifying the base-isolated structural damage by conducting a series of experimental tests on a scaled rubber-bearing isolated building model. To simulate the structural damage during the test, an innovative stiffness element device (SED) has been used to reduce the stiffness of the upper storey. Different damage scenarios under different earthquakes have been simulated and tested. Measured acceleration response data and the AEKF approach have been used to identify the unknown structural parameters and to track the variation of the stiffness in the upper storey during the test. The identified stiffness parameters based on the AEKF approach correlate reasonably well with that predicted by the finite-element method. Experimental studies conducted herein demonstrate that the AEKF approach is capable of tracking the variation of stiffness parameters from which the structural damage can be determined.
References
-
Narasimhan S., Nagarajaiah S., Gavin H., Johnson E. A. Smart base isolated benchmark building. Part I: Problem definition. Structural Control and Health Monitoring, Vol. 13, Issue 2-3, 2006, p. 573-588.
-
Nagarajaiah S., Narasimhan S., Johnson E. A. Structural control benchmark problem: phase ii – nonlinear smart base-isolated building subjected to near-fault earthquakes. Structural Control and Health Monitoring, Vol. 15, Issue 5, 2008, p. 653-656.
-
Tan R. Y., Huang M. C. System identification of a bridge with lead-rubber bearings. Computers and Structures, Vol. 74, 2000, p. 267-280.
-
Furukawa T., Ito M., Noori M. N. System identification of base-isolated building using seismic response data. Journal of Engineering Mechanics, Vol. 131, Issue 3, 2005, p. 268-273.
-
Yin Q., Zhou L., Yang J. N. An experimental study on AEKF method for health monitoring of base-isolated structures. Proceedings of Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Diego, CA, March 2010, Vol. 7647, p. 764709.
-
Yin Q., Zhou L., Mu T. F., Yan J. N. System identification of rubber-bearings based on experimental tests. Journal of Vibroengineering, Vol. 14, Issue 1, 2012, p. 315-324.
-
Lin J. W., Betti R., Smyth A. W., Longman R. W. On-line identification of nonlinear hysteretic structural system using a variable trace approach. Earthquake Engineering and Structural Dynamics, Vol. 30, 2001, p. 1279-1303.
-
Yang J. N., Pan S., Lin S. Least square estimation with unknown excitations for damage identification of structures. Journal of Engineering Mechanics, Vol. 133, Issue 1, 2007, p. 12-21.
-
Yin Q., Zhou L. Structural damage identification based on GA optimized least square estimation. Journal of Vibration and Shock, Vol. 29, Issue 8, 2010, p. 73-77.
-
Yang J. N., Lin S. L., Huang H. W., Zhou L. An adaptive extended Kalman filter for structural damage identification. Journal of Structural Control and Health Monitoring, Vol. 13, 2006, p. 849-867.
-
Zhou L., Wu S. Y., Yang J. N. Experimental study of an adaptive extended Kalman filter for structural damage identification. Journal of Infrastructure Systems, Vol. 14, Issue 1, 2008, p. 42-51.
-
Wu M. L., Smyth A. Real-time parameter estimation for degrading and pinching hysteretic models. International Journal of Nonlinear Mechanics, Vol. 43, Issue 9, 2008, p. 822-833.
-
Xie Z. B., Feng J. C. Real-time nonlinear structural system identification via iterated unscented Kalman filter. Mechanical Systems and Signal Processing, Vol. 28, 2012, p. 309-322.
-
Yang J. N., Huang H. W., Lin S. Sequential non-linear least-square estimation for damage identification of structures. International Journal of Non-linear Mechanics, Vol. 41, Issue 1, 2006, p. 124-140.
-
Yang J. N., Huang H. W., Pan S. W. Adaptive quadratic sum-squares error for structural damage identification. Journal of Engineering Mechanics, Vol. 135, Issue 2, 2009, p. 67-77.
-
Chang C. C., Shi Y. F. Identification of time-varying hysteretic structures using wavelet multiresolution analysis. International Journal of Nonlinear Mechanics, Vol. 45, Issue 1, 2010, p. 21-34.
-
Zhang K., Li H., Dua Z. D., Law S. S. A probabilistic damage identification approach for structures with uncertainties under unknown input. Mechanical Systems and Signal Processing, Vol. 25, 2011, p. 1126-1145.
-
Sato T., Chung M. Structural identification using adaptive Monte Carlo filter. Journal of Structural Engineering, JSCE, Vol. 51(A), 2005, p. 471-477.
-
Seyedpoor S. M. Structural damage detection using a multi-stage particle swarm optimization. Advances in Structural Engineering, Vol. 3, Issue 14, 2011, p. 533-549.
-
Nobahari M., Seyedpoor S. M. Structural damage detection using an efficient correlation-based index and a modified genetic algorithm. Mathematical and Computer Modeling, Vol. 53, 2011, p. 1798-1809.
About this article
This research is partially supported by the National Natural Science Foundation of China Grant No. 11172128, the Funds for International Cooperation and Exchange of the National Natural Science Foundation of China Grant No. 61161120323 and the US National Science Foundation Grant No. CMMI-0853395. And the writers would like to thank the support from Hengshui Zhentai Seismic Isolation Instrument Co., Ltd.
