Stability analysis and evaluation of Zengziyan in Jinfo Mountain under seismic (vibration) action

1. Introduction

With the continuous development of develop-the-west strategy in China at present, the large traffic constructions and human living continuously extend to the remote mountain area; meanwhile, many mountains with “coal measure strata” exist in southwestern China, where the overlying hard rock (limestone) is distributed with discontinuous weak structural planes and nearly orthogonal large steep dip joints, and the underlying soft rock (shale) is rich in coal, iron or bauxite resources. The mountains have been used for mining minerals for hundreds of years bringing serious hidden dangers of major geological disasters such as dangerous rock, debris flow and landslide to the southwestern China which becomes a major disaster area of traffic safety accidents.

The dangerous rock falling of Zenziyan in Jinfo Mountain, which is located at Nanchuan District of Chongqing, have occurred for many time over the years, and the dangerous rock is prone to collapse after storm, excessive rains or excessive sunny days. On June 3, 2001, the collapse of the rock mass occurred on a large scale; On August 12, 2004, the large-scale collapse of local rock mass occurred with volume of about 5000 m³; with the affection of Wenchuan earthquake on May 12, 2008, the collapse of dangerous rock at steep cliff combining site occurred causing no casualties fortunately. Now serious security hidden dangers are in partial dangerous rock mass with collapses on roof all the time endangering the lives and properties of surrounding villagers and mine safety. So the stability analysis and geological survey work of ZengZiyan have significant economic and social significance. The existing related researches show that the influencing factors affecting stability of ZengZiyan dangerous rock mass include the actions of mining, rainfall and groundwater, earthquake and improper blasting effect, etc., in which, big earthquake and improper blasting construction are the strong trigger factors causing unstability and collapse of dangerous rock mass. The influence of earthquake (vibration) on dangerous rock mass mainly displays in: 1) the dangerous rock in epicentral area subjected to vertical seismic force is more broken or unstabilized; 2) the dangerous rock mass is prone to unstability subjected to the horizontal seismic force, the size of which is closely related with the dangerous rock quality and seismic force coefficient, and the discussion of this paper is progressed mainly in view of this situation.

The responses such as acceleration, velocity, displacement, internal force and deformation of rock mass changing with time are produced by the excitation of earthquake or vibration, and the essence of seismic action is the inertial force produced in the rock mass by acceleration effect. The seismic (vibration) response of dangerous rock is decided by both seismic (vibration) characteristics and rock structural characteristics. The study and analysis for the stability of dangerous rock mass in earthquake-hit regions were carried out by some domestic scholars. The stabilities of several main dangerous rock masses at Zhaiziya in Longnan are qualitatively and quantitatively evaluated with geological analysis method and limit equilibrium method [1], and then the corresponding management schemes were put forward. The deformation monitoring data of T0-T6 crack zones at Lianziya in 2007-2009 were analyzed and processed [2], and the deformation characteristics and laws were shown in the form of figures.

Aiming at the characteristics of dangerous rock mass reinforced by prestressed anchor cables, the displacement field and stress field distributions of dangerous rock mass reinforced by prestressed anchor cables were simulated under different seismic loads [3], and the dynamic response and variations of reinforced dangerous rock mass were revealed. The stability and development trend of dangerous rock mass at Longgouwan were analyzed and predicted from the field investigation [4]. Most of these studies just stayed on the phase of field monitoring and evaluation with few seismic response analyses using analytical method. The closed analytical solution or semi-analytical solution of the seismic response analysis of rock strata can be obtained only when the model is simple [5-11]. The actual rock mass is abstracted into improved one-dimensional shear-beam model in this paper, and the definite problem of seismic response on stratified rock mass is solved to obtain the maximum response rules of absolute acceleration, shear stress and relative displacement of rock strata, then the practical monitoring data are taken to make contrastive analysis of the above calculation results and verify the rationality of stability evaluation using this analytic method to provide reference for the similar engineering construction designs.

2. Establishment and solution for the definite problem of seismic response

It is assumed that the horizontal rock strata are divided into $N$ layers, the densities respectively are ${\rho }_1$, ${\rho }_2$,…, ${\rho }_N$; the damping coefficients respectively are $c_1$, $c_2$,…, $c_N$; the dynamic shear modulus respectively are $G_1$, $G_2$,…, $G_N$; the thicknesses respectively are $h_1$, $h_2$,…, $h_N$. One horizontal seismic motion is in the bedrock with acceleration of $\ddot{u}\left(t\right)$ (shown in Fig. 1), now the displacement of rock strata only includes the horizontal shear displacement without bending displacement, thus the rock strata can be abstracted as a one-dimensional shear beam model.

Fig. 1Response diagram of rock strata (H0=0, H1=h1, H2=h1+h2, HN=h1+h2+…+hN)

The relative displacement of each rock stratum along $X$ direction is expressed with $V_n(n=\mathrm{1,2},...,N)$, and the rock element $dy$ is taken to be analyzed. When the damping effect is not considered, the following formula can be obtained according to the balance of forces in literature [12]:

In which, $Q$ is the shear of rock; $u$ is the displacement of rock; $A$ is the area of element; $t$ is the action time, Eq. (1) can be consolidated as:

The relation between $Q$ and $V_n$ is $Q=G_{n}A\left(\frac{\partial V_n}{\partial y}\right)$ substituted into Eq. (1), and then:

The wave equation of this problem can be obtained when the viscous damping force of rock is considered:

The boundary conditions of the above equation are that:

The displacement and stress continuity conditions are:

The initial conditions are:

When $c_n=$0, Eqs. (4)-(8) are the free vibration governing equation and conditions of system without considertion of damping.

The steady-state solution is assumed as $V_n=v_n\left(y\right)e^{i\omega t}$, $\text{(}{H}_{n-1}\le y\le H_n\text{,}n=\mathrm{1,2},...,N\text{)}$, which is substituted into Eq. (3), and the following formula can be obtained:

This is the linear homogeneous second-order differential equation with constant coefficients concerning $v_n\left(y\right)$, and the solution is:

where ${\lambda }_n=\sqrt{{\rho }_n/G_n}$, $l_n=(H_n+H_{n-1})/2\text{.}$ From the displacement continuity condition of Eq. (6), the following formula can be obtained:

where $a_n={\lambda }_n\omega L_n$, $L_n=(H_n-H_{n-1})/2$, $A_n$ and $B_n$ are undetermined coefficients. From the shear stress continuity condition of Eq. (6), the formula with condition of $y=H_n$ can be obtained:

where ${\alpha }_{n,n+1}=\sqrt{G_n{\rho }_n/G_{n+1}{\rho }_{n+1}}$, which is the impedance ratio between two adjacent rock strata. Eqs. (9)-(10) are solved to get that:

It can be written in matrix form:

where:

The relational expression of bottom and surface layers can be got by recurrence relation:

From the boundary conditions of Eq. (5), the following formula can be obtained:

The coefficient determinant of above formula equals to zero, and the frequency equation can be obtained:

The separation of variables is adopted in the solution of above problem, and the expression of solution is assumed as:

So the results after derivation are $\frac{{\partial }^{2}V}{\partial y^2}=-\sum _{i=1}^{\infty }{\left({\omega }_i{\lambda }_n\right)}^2{v}_{ni}\left(y\right)T_i\left(t\right)\text{,}$$\frac{{\partial }^{2}V}{\partial t^2}=\sum _{i=1}^{\infty }{T^{″}}_i\left(t\right)v_{ni}\left(y\right)$.

Eq. (21) is constantly satisfied with the boundary and continuity conditions of wave equation when c_nis constant, and it is substituted into Eq. (4), then:

Make ${\rho }_n=\rho \text{,}$ both sides of Eq. (4) times $v_{ni}dy$ and are integral along the thickness, meanwhile, the orthogonality of modal functions derived by Betti's laws is adopted, which is that:

The result after calculation can be obtained:

After further simplification and make $2{\mu }_m{\omega }_m=c/\rho$, then:

where ${\omega }_j$ is the undamped natural frequency; ${\mu }_j$ is the modal damping ratio; ${\eta }_j$ is the modal participation factor, which is:

The steady-state solution of Eq. (23) can be obtained:

Make $W_j\left(t\right)=-\left(1/{{\omega }^{\text{'}}}_j\right){\int }_0^t\ddot{u}\left(t\right)e^{-{\mu }_j{\omega }_j(t-\tau )}\mathrm{s}\mathrm{i}\mathrm{n}{{\omega }^{\text{'}}}_j(t-\tau )d\tau$, then the steady-state solution of Eq. (23) can be simplified as:

Eq. (25) is substituted into Eq. (21), and the relative displacement can be obtained:

The corresponding expressions of shear strain and absolute acceleration can be obtained after further derivation:

The integral operation should be carried out towards the above expressions in actual calculation, but the ground horizontal motion acceleration $\ddot{u}\left(t\right)$ is not a regular function, which can not be put in equations directly to integration, so the seismic response should be calculated by numerical method. The methods widely used at present are that the acceleration – time curve of a certain horizontal component recorded in earthquake is converted into the series of acceleration values concerning tiny time interval $\mathrm{\Delta }t$, and then the basic vibration equation is numerically integrated one at a time; finally, the corresponding maximum response figures are obtained by MATLAB programming. The formulas of Runge-Kutta method adopted in this paper are shown in literature [13].

3. Engineering example

The previous data and surface investigation show that the main rock mass in survey area of Zengziyan is limestone, which belongs to hard rock with strong karstification; the weak base under first-level steep cliff is Liangshan Formation carbonaceous shale, which belongs to soft rock and is prone to breakage and collapse by blasting vibration; the weak base under second-level steep cliff is Maokou Formation mixed shale limestone with soft and hard interphase. The bauxite is produced in the Lower Permian Liangshan Formation with ore body tendency of about 300°; the distances form lower boundary of Qixia Formation limestone are 0.44-2.58 m, and the distances form top boundary of Silurian Hanjiadian silty shale are 1.09-5.20 m. The ore deposits are continuous and stable with average thickness of 2.05 m and thickness variation coefficient of 48 %, which are mainly composed of earthy bauxite, dense bauxite, bean oolitic bauxite and chip gravel bauxite.

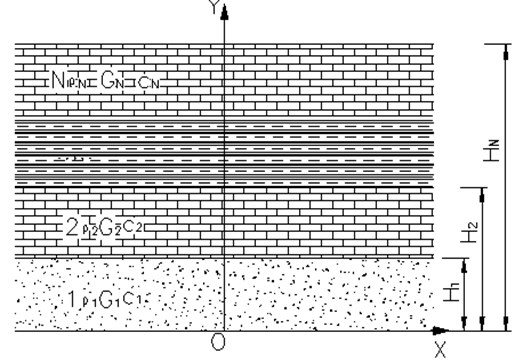
Limestone, shale and bauxite are taken in the simulation calculation with total height of $H=$140 m, and the rock physical parameters are shown in Table 1. The density of rock takes the average value of 1800 kg/m^-3, and the damping ratio of rock is $\mu =$0.01. One artificial seismic wave is input to the bedrock and the maximum response figures of absolute acceleration, shear stress and relative displacement are obtained (shown in Fig. 2).

Fig. 2Curves of maximum response

It can be seen from Fig. 3 that with the increase of height from bottom to top, the value of absolute acceleration increases from zero to certain extent followed by irregular fluctuation; the shear stress is the maximum at bedrock and decreases gradually until the top stratum; the relative displacement increases gradually form zero at the bedrock to the maximum value at the top stratum. So the upper rock masses of Zengziyan are most easily influenced by seismic (vibration) action, which have poor stability and incident shear rheology causing collapse.

Fig. 3Images of dangerous rocks at present

(a)

(b)

(c)

(d)

4. Evaluation and verification of stability

Now the monitoring results of monitoring station installed at the top of Zengziyan by Jinquan aluminum factory are collected (after the May 12, 2008), which are observed by theodolite with monitoring period of 9-30 days. The images of dangerous rocks at present are shown in Fig. 3, and the dynamic changes are shown in Table 2 and Fig. 4.

Fig. 4Curve of dangerous rock monitoring

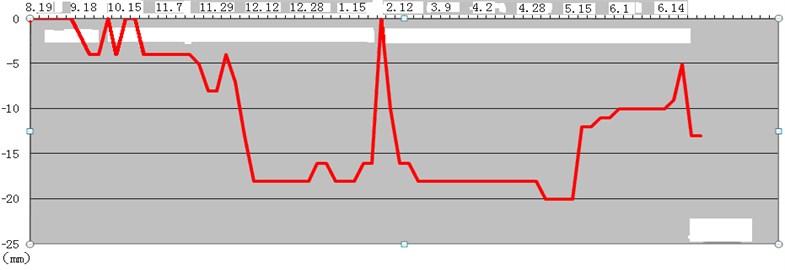
The estimated conclusions obtained from the above monitoring results and contrast analysis of stereographic projection are that: 1) the deformation of dangerous rock at survey area has already appeared showing the dangerous rock mass in unstable state, and the upper deformation is greater than the lower part; 2) the seismic intensities of survey area and Chongqing in 5.12 Wenchuan earthquake respectively are VI degree and V degree, and the influence of seismic forces is conducive to the formation of collapse; 3) several large dangerous rock masses are at Zengziyan mainly controlled by fractures, and the crack surfaces are uneven; 4) many crack surfaces have been run through with fracture widths of 3-20 cm, and most of the fractures are interlaminar fractures constituting the lower boundary of dangerous rock mass which is prone to produce dump-type or slip-type collapses; 5) the irregular jumps of curve in Fig. 5 are suspected to be caused by the blasting construction of aluminum factory. Because the destructive structural surface has been formed, the unstable or basically stable dangerous rock masses may accelerate the collapse under the actions of the rainstorm or vibrations in the near future, so the protective measures should be adopted in a timely manner.

In a word, the maximum seismic response rules of stratified rock mass obtained by simplified model can conform to the field monitoring results verifying the rationality and feasibility of analysis for the seismic response problem with shear-beam model.

5. Conclusion

(1) The actual rock mass is abstracted into improved one-dimensional shear-beam model in this paper, and the definite problem of seismic response on stratified rock mass is solved to obtain the maximum response rules of absolute acceleration, shear stress and relative displacement of rock strata. Combined with the lithologic characteristics of Zengziyan rock strata, the maximum response figures of rock are obtained by corresponding physical parameters.

(2) It can be seen from the comparative analysis for monitoring data of field investigation and evaluation that the maximum seismic response rules of stratified rock mass obtained by simplified model are accord with the field monitoring results well proving the rationality of the analytical results.

(3) Because the computed result is obtained by the abstraction and simplification of lithological characters without the consideration of influence of actual environmental and human factors (such as weathering, underground river, goaf unloading, etc.) on rock mass properties, therefore, the abstract model with comprehensive consideration of various environment and engineering factors more close to the actual situation is still to be further studied.