On the periodic solutions of the nonlinear oscillators

1. Introduction

Since the beginning of 1986, Zhou [1] and Pukhov [2] have developed a so-called differential transformation method (DTM) for electrical circuits problems. The method has been used extensively to solve effectively various linear and nonlinear ordinary, partial and integro-differential equations [3-16]. However this method has a difficulty when applied to differential equations with discontinuous terms. So the main purpose of the present research is not only to solve this difficulty but also to show how to obtain the approximate periodic solutions for nonlinear oscillators with discontinuities. To our best knowledge, there is no paper reported in the literature on the application of the differential transformation method to differential equations with discontinuities.

It is well known that DTM constructs the solution in the form of a truncated series which is periodic only in a very small region [17]. In order to overcome this difficulty, a reliable aftertreatment (AT) technique has been developed recently in [18] to obtain the approximate periodic solutions in a wider range. As shown in [18], the proposed aftertreatment technique splits into two types, named as (Sine-AT technique, SAT) and (Cosine-AT technique, CAT) and for illustration we will re-introduce the basic idea of the CAT technique which will be used in this paper. It was shown in [18] that the approximate periodic solutions have been obtained without any need for Pade approximants or Laplace transform which may give the SAT and CAT techniques some power if compared with the modified differential transform method [17, 19]. Very recently Merdan and Gokdoan [19] showed that the Cosine-AT and Sine-AT give same results obtained by using the modified differential transform method and the classical fourth-order Runge-Kutta (RK4) method.

The rest of this paper is organized as follows: in the next section (Section 2) a brief description of the one-dimensional DTM is provided; in Sections 3 the basic idea of the Cosine-aftertreatment technique is discussed; in Section 4 the proposed techniques are implemented to obtain the approximate periodic solutions for three nonlinear oscillators with discontinuities; in Sections 5 and 6 some conclusions are given.

2. One-dimensional differential transform

The differential transform of a function $x\left(t\right)$ is defined as follows:

In Eq. (1) $x\left(t\right)$ is the original function and $X\left(k\right)$ is the transformed function. The differential inverse transform of $X\left(k\right)$ is defined as:

So:

Eq. (3) implies that the concept of differential transform is derived from the Taylor series expansion. In actual applications the function $x\left(t\right)$ is expressed by a truncated series and Eq. (2) can be written as:

Some of the fundamental mathematical operations performed by the differential transform method are listed in Table 1.

3. Cosine-aftertreatment technique (CAT-technique)

If the truncated series given by Eq. (4) is expressed only in even-powers of the independent variable $t$, i. e.:

then the Cosine-aftertreatment technique (CAT-technique) is based on the assumption that this truncated series can be expressed as another finite series in terms of the cosine trigonometric functions with different amplitudes and frequencies:

where $n$ is finite.

Our main question here is how to find the values of ${\lambda }_j$ and ${\Omega }_j$, $j=0,\dots ,n.$ For answer we begin by expanding both sides of Eq. (6) as power series of $t$ to obtain:

Now the equation of the coefficients of like powers yields:

In practical applications it is sufficient to express the truncated series ${\Phi }_N\left(t\right)$ in terms of two or three cosines with different amplitudes and frequencies. If we choose to express ${\Phi }_N\left(t\right)$ as an approximate periodic solution in terms of two cosines with two different amplitudes, ${\lambda }_1$and ${\lambda }_2,$ and two different frequencies, ${\Omega }_1$ and${\Omega }_2$, we can rewrite Eq. (6) for $N=6$ and $n=2$ as:

In this case the four unknowns ${\lambda }_1,{\lambda }_2,{\Omega }_1$ and ${\Omega }_2$ can be determined by solving the following system of nonlinear algebraic equations analytically:

Moreover, if we choose to express ${\Phi }_N\left(t\right)$ as more accurate periodic solution in terms of three cosines, we can rewrite Eq. (6) for $N=10$ and $n=3$ as:

In this case the six unknowns ${\lambda }_1,{\lambda }_2,{\lambda }_3,{\Omega }_1,\mathrm{}{\Omega }_2$ and ${\Omega }_3$ can be determined by solving the following system of nonlinear algebraic equations numerically:

4. Applications

In this section we discuss the application of the DTM with the proposed Cosine-AT technique to obtain the periodic solutions of nonlinear oscillators with discontinuities. As explained in the previous section, the use of the Cosine-AT technique is based on obtaining the series solution of the problem under consideration as a finite polynomial in even powers of $t$.

4.1. Example 1

Consider the nonlinear oscillator with a discontinuous term [20-23]:

13

$\frac{d^{2}x}{{dt}^2}+x\left|x\right|=0,$

with the initial conditions:

14

$x\left(0\right)=a,\dot{x}\left(0\right)=0,a\ge 0.$

In Eq. (13) the major source of the difficulty in using the differential transformation method is the existence of the discontinuous term $\left|x\right|.$ In order to overcome this difficulty we introduce a new approach to deal with such term. Firstly we suppose that:

15

$f\left(x\right)=\left|x\right|,$

which can be written as:

16

$f^2\left(x\right)=x^2.$

We then take a differentiation with respect to $t$ to obtain:

17

$f\frac{df}{dt}=x\frac{dx}{dt}.$

By this Eq. (13) becomes:

18

$\frac{d^{2}x}{{dt}^2}+xf=0.$

Now by applying the differential transform to Eqs. (14), (17) and (18) we obtain the following recurrence scheme for $k\ge 0$:

19

$X\left(0\right)=a,X\left(1\right)=0,$
$F\left(0\right)=\left|x\left(0\right)\right|=a,$
$\left(k+1\right)\left(k+2\right)X\left(k+2\right)+\sum _{m=0}^{k}X\left(k-m\right)F\left(m\right)=0,$
$\sum _{m=0}^k\left(m+1\right)\left[F\left(m+1\right)F\left(k-m\right)-X\left(m+1\right)X\left(k-m\right)\right]=0.$

Using Eqs. (19) by taking $N=6$, we obtain a system of algebraic equations for $k=0,\dots ,4$. By solving this system for the values of $X\left(2\right),\dots ,X\left(6\right)$ by using Mathematica, we get:

20

$X\left(2\right)=-\frac{a^2}{2},X\left(3\right)=0,X\left(4\right)=\frac{a^3}{12},X\left(5\right)=0,X\left(6\right)=-\frac{a^4}{72}.$

From the inverse transformation rule Eq. (4) we can construct the following truncated series solution up to $t^6$:

21

${\Phi }_6\left(t\right)=a-\frac{a^2}{2}{t}^2+\frac{a^3}{12}{t}^4-\frac{a^4}{72}{t}^6.$

Since the truncated series ${\Phi }_6\left(t\right)$ given by the last equation is expressed as a polynomial in even powers of $t$, we can now deal with it by using the Cosine-AT technique. We assume an approximate periodic solution in the form:

22

${\Phi }_6\left(t\right)=\sum _{j=1}^2{\lambda }_j\cos \left({\Omega }_{j}t\right)={\lambda }_1\cos \left({\Omega }_{1}t\right)+{\lambda }_2\cos \left({\Omega }_{2}t\right).$

In order to find ${\lambda }_1,{\lambda }_2,{\Omega }_1$ and ${\Omega }_2,$ we insert $X\left(0\right),X\left(2\right),X\left(4\right)$ and $X\left(6\right)$ presented above into system Eq. (10) to get a system of four nonlinear algebraic equations. By solving this system analytically for ${\lambda }_1,{\lambda }_2,{\Omega }_1$ and ${\Omega }_2,$ we obtain:

23

${\lambda }_1=\frac{1}{20}\left(10-3\sqrt{10}\right)a,{\lambda }_2=\frac{1}{20}\left(10+3\sqrt{10}\right)a,$
${\Omega }_1=\sqrt{\left(4+\sqrt{10}\right)a},{\Omega }_2=\sqrt{\left(4-\sqrt{10}\right)a}.$

Therefore we can write the approximate periodic solution for the Eqs. (13-14) as:

24

$x_{\text{approx}}\left(t\right)=\frac{1}{20}\left(10-3\sqrt{10}\right)a\times \cos \left(\sqrt{\left(4+\sqrt{10}\right)a}t\right)+\frac{1}{20}\left(10+3\sqrt{10}\right)a$
$\times \cos \left(\sqrt{\left(4-\sqrt{10}\right)a}t\right).$

Here it should be noted that this approximate periodic solution is valid regardless of the oscillation amplitude $a$, i. e., for $0<a<+\infty$. In [20] the authors applied the parameter expansion method to Eqs. (13-14) and the following approximate periodic solution has been obtained:

25

$x=a\cos \left(\sqrt{\frac{8a}{3\pi }}t\right).$

Eq. (25) has been also obtained by the authors in [21] and [23] by using the max-min approach and He’s amplitude-frequency approach, respectively. The exact displacement of Eqs. (13-14) is given by [21]:

26

$x=a\cos \left[\frac{\pi \sqrt{6a}t}{2B\left(\frac{1}{2},\frac{1}{3}\right)}\right],$

where $B(*,*)$ denotes the Beta function.

In order to check the effectiveness of our approach we compare our result Eq. (24) with the approximate periodic solution obtained by the parameter-expansion and the max-min methods, given by Eq. (25) and the exact displacement Eq. (26) in Figs. 1-4 at different values of $a=1,10,100,1000$. From these figures it can be concluded that the suggested approach with the Cosine-AT technique leads to approximate periodic solutions with good accuracy for all amplitudes.

Fig. 1Comparison of the present approach, Eq. (24) with the parameter-expansion method [20], Eq. (25) and the exact solution (max-min [21]), Eq. (26) for example 1, at a=1

Fig. 2Comparison of the present approach, Eq. (24) with the parameter-expansion method [20], Eq. (25) and the exact solution (max-min [21]), Eq. (26) for example 1, at a=10

Fig. 3Comparison of the present approach, Eq. (24) with the parameter-expansion method [20], Eq. (25) and the exact solution (max-min [21]), Eq. (26) for example 1, at a=100

Fig. 4Comparison of the present approach, Eq. (24) with the parameter-expansion method [20], Eq. (25) and the exact solution (max-min [21]), Eq. (26) for example 1, at a=1000

4.2. Example 2

Consider the nonlinear oscillator with a discontinuous term [24-25]:

27

$\frac{d^{2}x}{{dt}^2}+x+\epsilon x\left|x\right|=0,ϵ>0,$

with the initial conditions:

28

$x\left(0\right)=a,\dot{x}\left(0\right)=0.$

By the same analysis as in the previous example, we can easily obtain the following recurrence scheme for $k\ge 0$:

29

$X\left(0\right)=a,X\left(1\right)=0,$
$F\left(0\right)=\left|x\left(0\right)\right|=a,$
$\left(k+1\right)\left(k+2\right)X\left(k+2\right)+X\left(k\right)+ϵ\sum _{m=0}^{k}X\left(k-m\right)F\left(m\right)=0,$
$\sum _{m=0}^k\left(m+1\right)\left[F\left(m+1\right)F\left(k-m\right)-X\left(m+1\right)X\left(k-m\right)\right]=0.$

Using the above relations by taking $N=6$, we obtain a system of algebraic equations for $k=0,\dots ,4$. By solving this system for the values of $X\left(2\right),\dots ,X\left(6\right)$, we get:

30

$X\left(2\right)=-\frac{1}{2}\left(1+ϵa\right)a,X\left(3\right)=0,X\left(4\right)=\frac{1}{24}\left(1+3ϵa+2{ϵ}^2{a}^2\right)a,X\left(5\right)=0,$
$X\left(6\right)=-\frac{1}{720}\left(1+11ϵa+20{ϵ}^2{a}^2+10{ϵ}^3{a}^3\right)a.$

Hence we have the following truncated series solution up to $t^6$:

31

${\Phi }_6\left(t\right)=a-\frac{1}{2}\left(1+ϵa\right)a{t}^2+\frac{1}{24}\left(1+3ϵa+2{ϵ}^2{a}^2\right)a{t}^4$
$-\frac{1}{720}\left(1+11ϵa+20{ϵ}^2{a}^2+10{ϵ}^3{a}^3\right)a{t}^6.$

Here ${\Phi }_6\left(t\right)$ is also expressed as a polynomial in even powers of $t$ and as shown in the previous example we can deal with it by using the Cosine-AT technique. We also assume an approximate periodic solution in the form of Eq. (22). This leads to the approximate periodic solution:

32

$x_{\text{approx}}\left(t\right)=\frac{\left(5+6ϵa+\sqrt{25+64ϵa+40{ϵ}^2{a}^2}\right)a}{2\sqrt{25+64ϵa+40{ϵ}^2{a}^2}}$
$\times \cos \left(\sqrt{\frac{1}{2}\left(7+8ϵa-\sqrt{25+64ϵa+40{ϵ}^2{a}^2}\right)}t\right)$
$+\frac{\left(-5-6ϵa+\sqrt{25+64ϵa+40{ϵ}^2{a}^2}\right)a}{2\sqrt{25+64ϵa+40{ϵ}^2{a}^2}}$
$\times \cos \left(\sqrt{\frac{1}{2}\left(7+8ϵa+\sqrt{25+64ϵa+40{ϵ}^2{a}^2}\right)}t\right),$

which is also periodic for any given values of $ϵ$ and $a$. The approximate periodic solution obtained by the variational iteration method [24] is given by:

33

$x=a\cos \left(\sqrt{\frac{8ϵa}{3\pi }}t\right).$

Fig. 5Comparison of the present approach, Eq. (32) with the variational iteration method, Eq. (33) and the numerical solution for example 2, at ϵ=0.1 and a=1

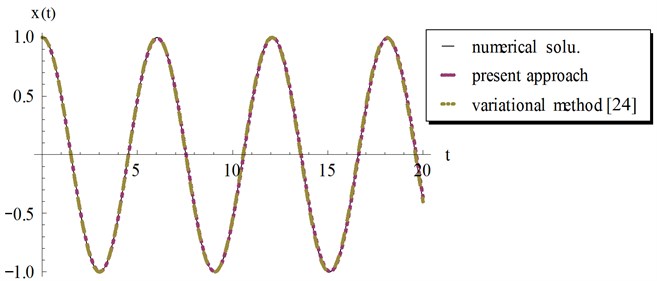
Fig. 6Comparison of the present approach, Eq. (32) with the variational iteration method, Eq. (33) and the numerical solution for example 2, at ϵ=0.2 and a=10

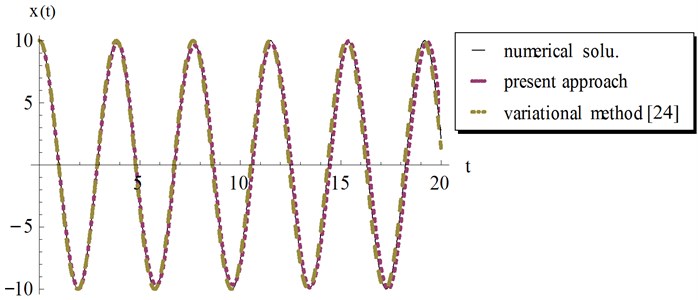
Fig. 7Comparison of the present approach, Eq. (32) with the variational iteration method, Eq. (33) and the numerical solution for example 2, at ϵ=0.3 and a=100

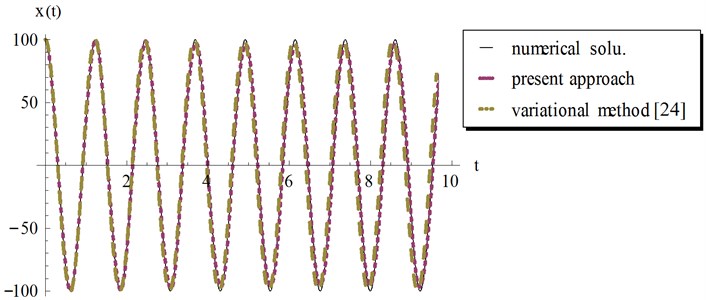
Fig. 8Comparison of the present approach, Eq. (32) with the variational iteration method, Eq. (33) and the numerical solution for example 2, at ϵ=0.01 and a=1000

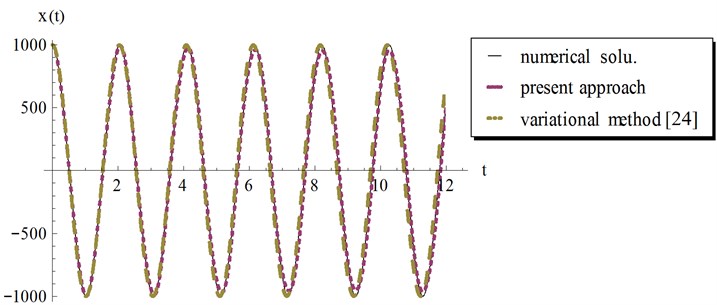
In Figs. 5-8 we compared our analytical approximate periodic solution in Eq. (32) with the variational iteration result Eq. (33) and the numerical solution obtained by Mathematica using the “NDSolve” command. It can be observed from these figures that our result in Eq. (32) provides excellent agreement with variational iteration method and the numerical solution regardless of the oscillation amplitude $a$.

4.3. Example 3

This example considers the following equation [24, 25]:

34

$\frac{d^{2}x}{{dt}^2}+\beta x^3+\epsilon x\left|x\right|=0,ϵ>0,$

with the initial conditions:

35

$x\left(0\right)=a,\dot{x}\left(0\right)=0,$

where the parameter $\beta$ is considered real. Proceeding as above, we obtain for $k\ge 0$:

36

$X\left(0\right)=a,X\left(1\right)=0,$
$F\left(0\right)=\left|x\left(0\right)\right|=a,$
$\left(k+1\right)\left(k+2\right)X\left(k+2\right)+\beta \sum _{m=0}^k\sum _{l=0}^{m}X\left(k-m\right)X\left(m-l\right)X\left(l\right)+ϵ\sum _{m=0}^{k}X\left(k-m\right)F\left(m\right)=0,$
$\sum _{m=0}^k\left(m+1\right)\left[F\left(m+1\right)F\left(k-m\right)-X\left(m+1\right)X\left(k-m\right)\right]=0.$

Using $N=6$, a system of algebraic equations is obtained for $k=0,\dots ,4$. On solving this system for $X\left(2\right),\dots ,X\left(6\right),$ yields:

37

$X\left(2\right)=-\frac{1}{2}\left(ϵ+\beta a\right)a^2,X\left(3\right)=0,X\left(4\right)=\frac{1}{24}\left(3{\beta }^2{a}^2+5ϵ\beta a+2{ϵ}^2\right)a^3,$
$X\left(5\right)=0,X\left(6\right)=-\frac{1}{720}\left(27{\beta }^3{a}^3+63ϵ{\beta }^2{a}^2+46{ϵ}^2\beta a+10{ϵ}^3\right)a^4.$

Therefore the approximate series solution can be written as:

38

${\mathrm{\Phi }}_6\left(t\right)=a-\frac{1}{2}\left(ϵ+\beta a\right)a^2{t}^2+\frac{1}{24}\left(3{\beta }^2{a}^2+5ϵ\beta a+2{ϵ}^2\right)a^3{t}^4$
$-\frac{1}{720}\left(27{\beta }^3{a}^3+63ϵ{\beta }^2{a}^2+46{ϵ}^2\beta a+10{ϵ}^3\right)a^4{t}^6,$

which is also expressed as a polynomial in even powers of $t$. The Cosine-AT technique leads to the approximate periodic solution:

39

$x_{\text{approx}}\left(t\right)=\frac{\left({\mu }_1+\sqrt{\sigma }\right)a}{2\sqrt{\sigma }}\cos \left(\sqrt{\frac{\left({\mu }_2-\sqrt{\sigma }\right)a}{2\tau }}t\right)+\frac{\left(-{\mu }_1+\sqrt{\sigma }\right)a}{2\sqrt{\sigma }}\cos \left(\sqrt{\frac{\left({\mu }_2+\sqrt{\sigma }\right)a}{2\tau }}t\right),$

where ${\mu }_1,{\mu }_2,\sigma$ and $\tau$ are given as:

40

${\mu }_1=20{\beta }^2{a}^2+25ϵ\beta a+6{ϵ}^2,{\mu }_2=24{\beta }^2{a}^2+31ϵ\beta a+8{ϵ}^2,\tau =ϵ+2\beta a,$
$\sigma =432{\beta }^4{a}^4+1080ϵ{\beta }^3{a}^3+937{ϵ}^2{\beta }^2{a}^2+328{ϵ}^3\beta a+40{ϵ}^4.$

In [24] the approximate periodic solution was obtained by using the variational iteration method and given by:

41

$x=a\cos \left(\sqrt{\frac{3\beta a^2}{4}+\frac{8ϵa}{3\pi }}t\right).$

It should be noted that the solution Eq. (39) is always periodic under the two conditions:

42

$\sigma >0,{\mu }_2-\sqrt{\sigma }>0,{\mu }_2+\sqrt{\sigma }>0,\tau >0,$

and:

43

$\sigma >0,{\mu }_2-\sqrt{\sigma }<0,{\mu }_2+\sqrt{\sigma }<0,\tau <0.$

Examples for the values of $\beta$ and $ϵ$ that satisfy these conditions are shown graphically by Fig. 9 at different values of the amplitude $a$. The numerical results are depicted and compared with other solutions in Figs. 10-13 at different values of $a$. The results show that at $a=1$ the Cosine-after treatment technique agrees with the other methods in a wider range of $t.$ However this agreement decreases with increasing $a$. It may be concluded that at large values of $a$ we have to increase the accuracy of our technique by increasing $n$ in Eq. (6).

Fig. 9Examples for the values of β and ϵ

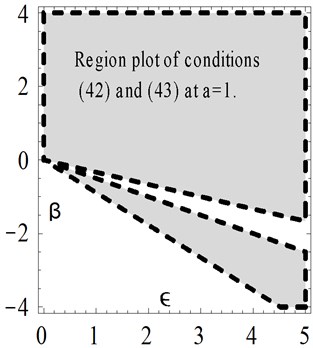
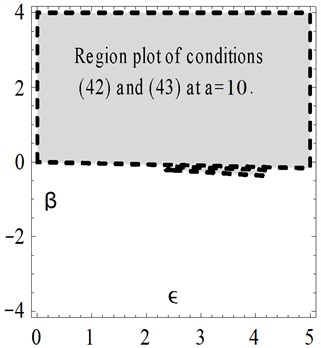
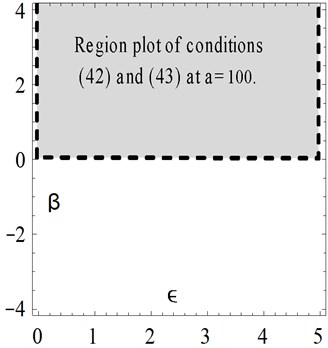
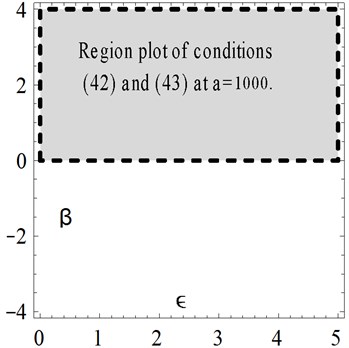
Fig. 10Comparison of the present Cosine aftertreatment technique, CAT-Tech., Eq. (39) with the variational iteration method, Eq. (41) for example 3, at a=1, β=-0.5 and ϵ=4

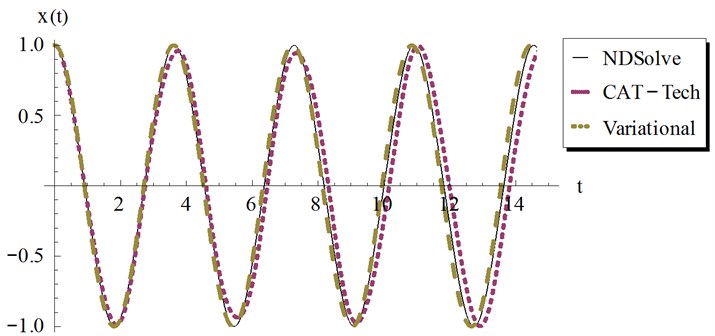
Fig. 11Comparison of the present Cosine aftertreatment technique, CAT-Tech., Eq. (39) with the variational iteration method, Eq. (41) for example 3, at a=10, β=1 and ϵ=3

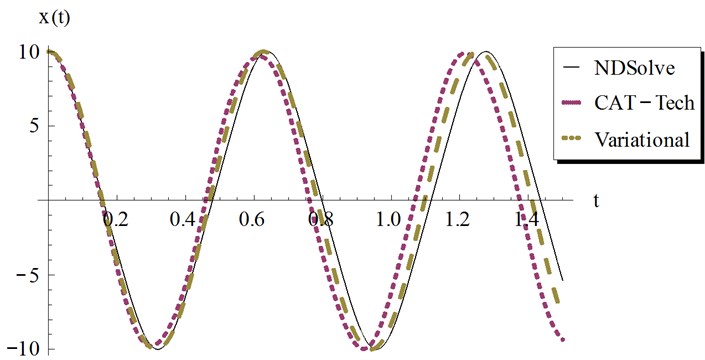
Fig. 12Comparison of the present Cosine aftertreatment technique, CAT-Tech., Eq. (39) with the variational iteration method, Eq. (41) for example 3, at a=100, β=3 and ϵ=4

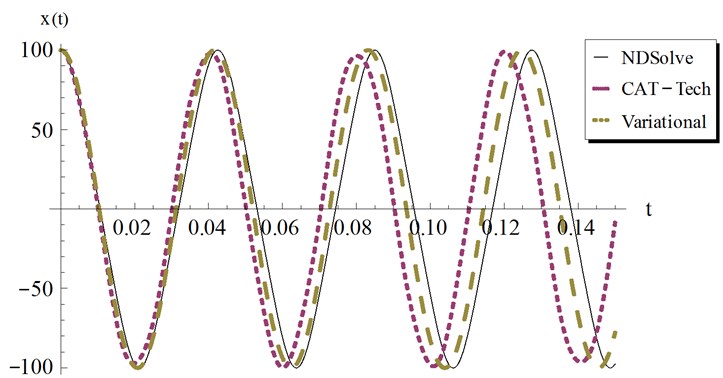
Fig. 13Comparison of the present Cosine aftertreatment technique, CAT-Tech., Eq. (39) with the variational iteration method, Eq. (41) for example 3, at a=1000, β=3 and ϵ=4

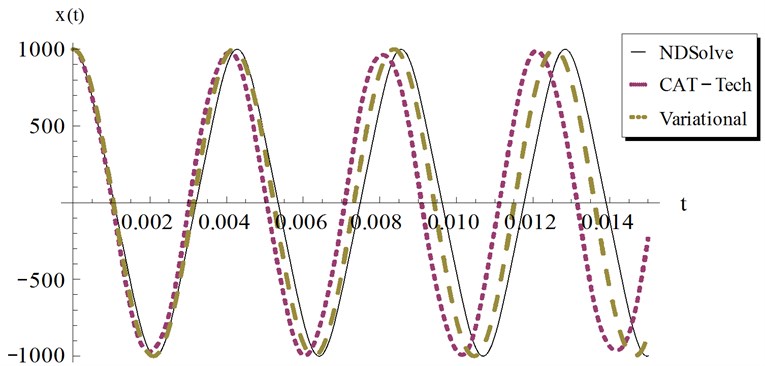
5. Remarks

In several papers [26-30] many authors showed that the DTM is nothing more than a disguised version of the Taylor series method. In this regard we agree with their point of view in the case when the DTM and Taylor series are applied to search for a series solution for a differential equation in which the discontinuous terms are not involved. However, it may be difficult to directly apply Taylor series method to obtain the series solutions for the present class of ordinary differential equations with discontinuous terms.

6. Conclusions

To our best knowledge, this is the first paper reported on the application of the differential transformation method to nonlinear oscillators with discontinuities. A new approach has been proposed to overcome the difficulty arising from the existence of the discontinuous terms. Three examples are solved and the obtained results demonstrate that the discontinuous function will not affect much the effectiveness and convenience of the differential transformation method.