Effect of non-homogeneity on free vibration of visco-elastic rectangular plate with varying structural parameters

1. Introduction

Non-homogeneous plates of variable thickness are vigorously used in engineering and architectural practice i.e. in the designs of space vehicle, marine, automobile etc. Non-homogeneity along with variable thickness not only reduce the cost of the material but also provide more strength, lighten the loads, increase reliability etc. of the structures.

Most of the mechanical structures work under the influence of temperature i.e. missiles, nuclear reactor etc. which changes the mechanical properties of the material. Therefore, effect of temperature on the vibration of structures can not be neglected.

Since a lot of factors directly affect the vibrational properties of materials or plates, they must be analyzed from engineering perspective with easy and fast computational technique for the betterment of structures.

In available literature, remarkable work is found in the field of vibration of plates of variable thickness. Bambill et al. [1] discussed transverse vibration of an orthotropic rectangular plate of linearly varying thickness and with a free edge. Chakraverty and Petyl [3] used two-dimensional orthogonal polynomial to find out natural frequencies for free vibration of non-homogeneous elliptical and circular plates. Hosseini [4] presented an analytical solution for free vibration analysis of stepped circular and annular FG plates. Hasheminejad et al. [5] analyzed asymmetric free vibration of coupled system including clamped circular plate in contact with incompressible bounded fluid. Gupta and Khanna [6] investigated vibration of visco-elastic rectangular plate with linearly thickness variation in both directions. Gupta and Khanna [7] discussed free vibration of clamped visco-elastic rectangular plate having bi-directional parabolic thickness variation. Gupta et al. [8] worked on free vibration of clamped visco-elastic rectangular plate having bi-directional exponentially thickness variations. Khanna et al. [9] observed the effect of varying poisson ratio on thermally induced vibrations of non-homogeneous rectangular plate. Lal et al. [10] used boundary characteristic orthogonal polynomials to analyze transverse vibrations of non-homogeneous rectangular plates. Lal and Yajuvindra [11] studied transverse vibration of orthotropic plates of bilinearly varying thickness. Leissa [12] provided excellent data for vibration of plates of different shapes with different boundary conditions in his monograph. Leissa and Chern [14] analyzed forced vibration response of plates. Li [15] analyzed vibration of visco-elastic plates with general elastic boundary supports. Mukat [16] used Rayleigh Ritz method for free vibration of super elliptical plates of variable thickness. Patel et al. [17] presented appericiable work on study of vibrational behaviour of rectangular plate with angle shaped stiffeners. Tariverdilo [18] analyzed asymmetric free vibration of coupled system including clamped circular plate in contact with incompressible bounded fluid.

The objective of present study is to analyze the effect of varying strucutral parameters i.e. non homogeneity constant, taper constant, thermal gradient and aspect ratio on free vibration of visco-elastic rectangular plate. Numerical results for first two modes of frequency are computed with the help of ‘Mathematica’ and are given in tabular as well as in graphical form.

2. Theory and method of analysis

Fundamental equations for the free vibration of visco-elastic rectangular plate are entitled in this section.

The equation of motion of a visco-elastic plate of variable thickness is [2]:

where:

Using Eq. (2) in Eq. (1), one gets:

where, ${\diamond }^4(D_1,w)=\frac{{\partial }^2{D}_1}{\partial y^2}\frac{{\partial }^{2}w}{\partial x^2}-2\frac{{\partial }^2{D}_1}{\partial x\partial y}\frac{{\partial }^{2}w}{\partial x\partial y}+\frac{{\partial }^2{D}_1}{\partial x^2}\frac{{\partial }^{2}w}{\partial y^2}$, is die operator, and ${\nabla }^2\equiv \frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2},$ is the Laplacian operator.

By using variable separation technique, the solution of Eq. (3) can be taken as:

Substituting Eq. (4) into Eq. (3), one obtains:

Here, dot denotes differentiation with respect to $t$.

The preceding equation is satisfied if both of its sides are equal to a positive constant. Denoting this constant by ${\omega }^2$, one gets:

Eq. (6) and Eq. (7) are differential equations of motion and time function for visco-elastic rectangular plate respectively.

Here, $D_1$ is flexural rigidity of rectangular plate i.e.:

3. Limitations

Since the scope of the study of vibration of plate is too vast to consider as whole, a lot of limitations are required to make easy and fast calculation for the natural frequency for various values of varying structural parameters. The following limitations are taken in the present study:

a) Authors assumed the exponential temperature variation in $x$-direction as:

The temperature dependence of the modulus of elasticity for most of engineering materials can be expressed as:

where, $E_0$ is the value of the Young's modulus at reference temperature i.e. $\tau =0$ and $\gamma$ is the slope of the variation of $E$ with $\tau$. After substituting $\tau$ form Eq. (9), Eq. (10) becomes:

where, $\alpha =\gamma {\tau }_0(0\le \alpha <1)$, is thermal gradient.

b) It is assumed that thickness varies exponentially in $x$-direction as [8]:

c) It is considered that poisson’s ratio of material also varies exponentially in $x$-direction as [9]:

where, ${\nu }_0$ denotes poisson ratio at reference temperature and ${\alpha }_1$ is non-homogeneity constant. Since maximum value of poisson ratio is less than equal to 1/2, numeric value of ${\alpha }_1$ (as it varies exponentially in this paper) can not be greater than 0.16 (approximately). Hence, variation in poisson ratio is taken from 0.0 to 0.15 (at most) in calculation.

After substituting the values of $E$, $h$ and $\nu$ from equation (11), (12) and (13) in equation (8), one obtains:

d) Plate is supposed to be clamped at all the edges, so boundary conditions are [6]:

To satisfy Eq. (15), corresponding two-term deflection function is taken as [6]:

where, ${\varphi }_1$ and ${\varphi }_2$ are arbitrary constants.

4. Solution of frequency equation

To get better accuracy and efficiency of results, Rayleigh Ritz method is applied to solve the frequency equation. This method is based on principle of conservation of energy i.e. maximum strain energy $\left(P_E\right)$ must be equal to the maximum kinetic energy $\left(K_E\right)$. So it is necessary for the problem under consideration that [7]:

where:

Now assuming the non-dimensional variables as:

Using Eq. (20) in Eq. (18) and Eq. (19), one gets:

where $Q=\frac{E_0{h}_0^3}{24a^2}.$

Using Eq. (21) and Eq. (22) in Eq. (17), one obtains:

Here, ${\lambda }^2=\frac{12\rho {\omega }^2{a}^4}{E_0{h}_0^2}$, is frequency parameter. Equation (23) consists two unknown constants i.e. ${\varphi }_1$ and ${\varphi }_2$ arising due to the substitution of $W$. These two constants are to be determined as follows:

On simplifying Eq. (24), one gets:

where, $Q_{n1},Q_{n2}(n=\mathrm{1,2})$ involve structural parameters and frequency parameter.

For a non-trivial solution, the determinant of the coefficient of equation (25) must vanish. Therefore, frequency equation comes as:

Since equation (26) is a quadratic equation in ${\lambda }^2$, one can easily calculate both the roots of Eq. (26) i.e. two values of ${\lambda }^2$. From these two values of ${\lambda }^2$, one can easily obtain two values of $\lambda$ i.e. ${\lambda }_1$ and ${\lambda }_2$ which represent first and second mode of the fundamental frequency respectively.

5. Numeric results and discussion

First two modes of frequency are calculated by Mathematica for different combinations of varying structural parameters.

Results for both the modes of frequency with increasing value of taper constant $\left(\beta \right)$ from 0.0 to 1.0 at fixed aspect ratio $\left(a/b=1.5\right)$ are collected in Table 1 for the following cases:

i) $\alpha ={\alpha }_1=0.0$,

ii) $\alpha =0.2,{\alpha }_1=0.1$.

A continuous growth is found for both the modes of frequency as $\beta$ increases from 0.0 to 1.0 in both the cases. Also, it is interesting to note that frequency (for both the modes of vibration) increases as combined values of $\alpha$ and ${\alpha }_1$ increase.

Frequency for first two modes of vibration with respect to varying thermal gradient $\left(\alpha \right)$ from 0.0 to 0.8 at fixed aspect ratio $\left(a/b=1.5\right)$ is given in Table 2 for the following cases:

iii) $\beta ={\alpha }_1=0.0$,

iv) $\beta =0.2;{\alpha }_1=0.1$.

It is clearly seen that frequency (for both the modes) increases continuously in both the cases as $\alpha$ increases from 0.0 to 0.8. Also, authors note that rate of increment in frequency in Table 2 is slightly less as compared to table 1 for both cases.

First two modes of frequency at fixed aspect ratio $\left(a/b=1.5\right)$ are tabulated in Table 3 with increasing values of ${\alpha }_1$ from 0.0 to 0.15 for the following cases:

v) $\alpha =\beta =0.0$,

vi) $\alpha =\beta =0.2$.

Here, authors analyzed a very slow but continuous increment in frequency (for both the modes) as ${\alpha }_1$ increases from 0.0 to 0.15. Again, frequency increases when $\alpha$ and $\beta$ increase simultaneously from 0.0 to 0.2.

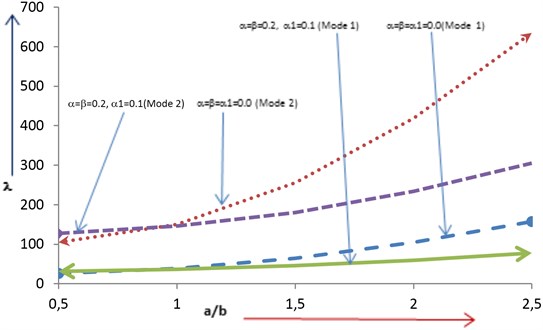
Frequency for first two modes of vibration is placed in Table 4 with increasing values of aspect ratio from 0.5 to 2.5 for the following cases:

vii) $\alpha =\beta ={\alpha }_1=0.0$,

viii) $\alpha =\beta =0.2;{\alpha }_1=0.1$.

As aspect ratio increases, authors observed that frequency increases rapidly for both the modes in both the cases. Further, an increment in frequency is found when simultaneous values of varying parameters increase from case (vii) to case (viii).

Variations in frequency (for both the modes of vibration) in Table 1, 2, 3 and 4 are also shown in Fig. 1, 2, 3 and 4 respectively.

Fig. 1Frequency Vs Taper Constant for fixed aspect ratio (a/b=1.5)

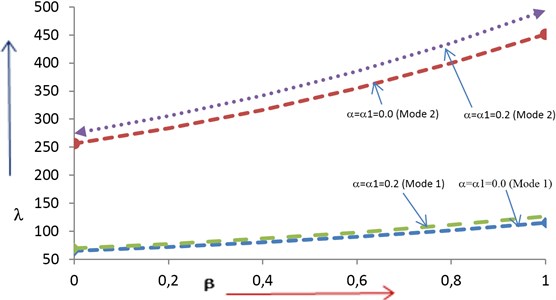
Fig. 2Frequency Vs Thermal Gradient for fixed aspect ratio (a/b=1.5)

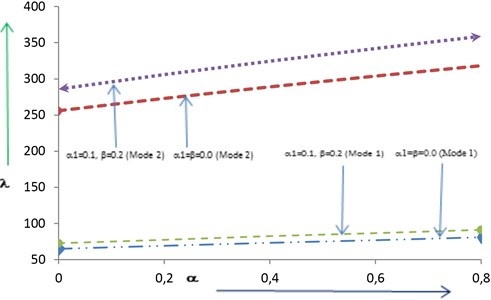
Fig. 3Frequency Vs Non-Homogeneity Constant for fixed aspect ratio (a/b=1.5)

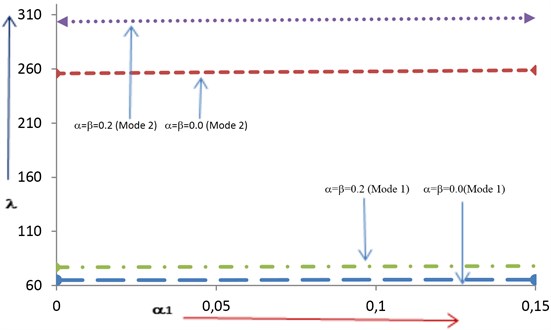
Fig. 4Frequency Vs Aspect Ratio

6. Comparisons

On comparing the results of present paper with [9] (linear thickness variation and bi-linear temperature variation) for corresponding values of structural parameters, authors found an excellent agreement as follows:

Table 5 shows that frequency (for both the modes of vibration) is slightly greater in present paper as compared to [9] with increasing value of $\beta$ at $\alpha ={\alpha }_1=0.0$ and $a/b=1.5$.

In table 6, authors observed that frequency (for both the modes of vibration) in the present paper is greater than [9] with increasing value of thermal gradient at ${\alpha }_1=\beta =0.0$ and $a/b=1.5.$

Frequency for both the modes of vibration for present paper and [9] is given in table 7 with varying aspect ratio for the following cases:

i) $\alpha =\beta ={\alpha }_1=0.0,$

ii) $\alpha =\beta =0.2;{\alpha }_1=0.0$.

In case (i), no change is found between the results of present paper and [9]. In case (ii), an increment is found in frequency for both the modes of vibration for present paper as compared to [9].

7. Conclusions

Due to unavailability of numerical data about first few modes of frequency, sometimes engineers or researchers are forced to drop their project or designs. Hence, it becomes necessary to provide some mathematical models for their help.

In the present study, results for first two modes of frequency parameter are computed using MATHEMATICA within the permissible range of varying structural parameters. Here, authors suggest design engineers or researchers to analyze the findings of the present paper before finalizing any design or structure. Also, authors assure that required frequency can be obtained by choosing appropriate values of structural parameters.