Nonlinear resonances of electrostatically actuated nano-beam

Liu, Canchang; Yue, Shuchang; Xu, Yingzi

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 August 2014

Check for updates

Nonlinear resonances of electrostatically actuated nano-beam

Canchang Liu¹

Shuchang Yue²

Yingzi Xu³

^{1, 2, 3}School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo, 255049, China

Corresponding Author:

Canchang Liu

Cite the article Download PDF

Downloads 1193

Abstract

Nonlinear response of electrostatically actuated nano-beam near-half natural frequency is studied by considering the nonlinearities of the large deformation, electrostatic force and Casimir effect. A first-order fringe correction of the electrostatic force, large deformation, viscous damping, and Casimir effect are included in the dynamic model. The dynamics of the resonator are investigated by using the method of multiple scales in a direct approach to the problem. The sufficient conditions of guaranteeing the system stability and a saddle-node bifurcation are studied. The influences of large deformation, damping, actuation, and fringe effect on the resonator response are studied. The peak amplitude of the primary resonance is given in the paper. Numerical simulations are conducted for uniform nano-beam.

1. Introduction

Micro-electromechanical systems (MEMS) devices have been investigated thoroughly in the literature for their potential to build high sensitive sensors [1], probes [2], filters [3], and resonators [4-6]. MEMS devices have several advantages that are related to their fabrication technology allowing them to be compatible with the complementary metal oxide semiconductor (CMOS) processes [7, 8]. This advantages result into low power consumption, lower cost [9], increasing manufacturability and reliability, and enabling single chip solutions. Resonators made of simply-simply supported beam have been modeled and measured by various research groups [10-11].

Nano beams have long been considered ideal building blocks for nano-electromechanical systems’ (NMES) devices because of their superior electromechanical properties. Some of the NMES devices can be simply modeled as cantilevers or fixed-fixed beams hanged over an infinite conductive substrate. These slender nano beams are excited via electrostatic or magnetomotive forces. As the excitation magnitude increases, nanotube resonators display distinctive nonlinear characteristics due to the relatively small dimensions of nano-devices. The effective resonance bandwidth of such devices can be altered due to the presence of nonlinearities [12]. Some nano beams can transform a planar motion into a motion of whirling [13]. These nonlinear behaviors may have detrimental effect on the nano-devices.

The stability of the nonlinear systems and the types of nonlinearities are highly sensitive to physical parameters, initial amplitude, and excitation frequency [5, 6, 14]. It is important to identify bifurcation points and bifurcation parameters in order to design and control systems under parametric excitation [14, 15]. A double-sided electro mechanically driven nanotube resonator taking into account the Van der Waals force has been investigated [16]. An energy-based method has been used to create analytical relationships for the steady-state amplitude of the nanotube as a function of driving frequency and excitation voltage. The nonlinear response of electrostatically actuated cantilever beam micro-resonators near-half natural frequency was analyzed by considering the nonlinearities of the forces of electrostatic and Casimir [17]. Reduced order model analysis of frequency response of AC near half natural frequency electrostatically actuated MEMS cantilever was studied.

Optical experimental investigation of movable microsystem components was studied by using time-averaged holography. A deeper insight into computational and experimental interpretation of time-averaged MEMS hologram was provided by the analytical results between parameters of the chaotic oscillations and the formation of time-averaged fringes [18].

Nonlinearities play a significant role in nano scale. The nonlinearities arise from a number of sources such as large deflections (geometric nonlinearities), electrostatic actuation, and Casimir effect. These slender nano beams are suspended over a trench and excited via electrostatic or magnetomotive forces. Nano beams resonators display distinctive nonlinear characteristics due to the relatively small dimensions of nano beams. Electrostatic actuation can create a variety of nonlinear parametric resonances depending on system parameters, excitation frequency, and excitation voltage.

The nonlinearities of the large deformation, electrostatic force and Casimir effect are taken into account in the analysis of the nonlinear response of electrostatically actuated nano-beam near-half natural frequency. The first-order fringe correction of the electrostatic force, large deformation, viscous damping, and Casimir effect are included in the model. The method of multiple scales is used directly in the analysis of the partial-differential equation of motion and boundary conditions of the resonator. The sufficient conditions for the stability of the system and a saddle-node bifurcation are given. The influences of large deformation, damping, actuation, and fringe effect on the resonator response are discussed. Numerical simulations are conducted for uniform nano-beam.

2. Partial-differential equation of motion

A flexible nano-beam suspended over a grounded substrate is considered (Fig. 1). The beam is electrostatically actuated by applying an alternating voltage between the beam and the underlying plate. This paper investigates the case in which there is no DC polarizing voltage and with only the AC voltage present. The AC voltage will still contribute to the static voltage component. In addition to the electrostatic force, viscous damping and Casimir effect are considered. The length of the beam is relatively large compared to the width and thickness. Therefore, Euler-Bernoulli hypothesis holds. Considering the nonlinear vibration of the system, the partial-differential equation of motion and boundary conditions can be written as [17, 19]:

1

ρ A \frac{\partial^{2} w}{\partial {t^{'}}^{2}} + E I u^{″ ″} = \frac{E A}{2 l} \int_{0}^{l} {w^{'}}^{2} d x w^{″} + \frac{π^{2} ℏ c W}{240 {(g - w)}^{4}} + b^{*} \frac{\partial w}{\partial t^{'}}

+ \frac{ε_{0} W}{2} \frac{V {(t^{'})}^{2}}{{(g - w)}^{2}} (1 + 0.65 \frac{g - w}{W}),

where $w (x, t')$ is the transverse displacement of the beam. $x$ and $l$ are longitudinal coordinate and beam's length, respectively. $E$ , $A$ , $I$ , and $ρ$ are Young’s modulus, cross-sectional area, cross sectional moment of inertia, and material density, respectively. $b^{*}$ is the coefficient of viscous damping per unit length. $W$ is the beam width, g is the initial gap between the beam and ground electrode, and $V$ is the applied voltage. $ℏ = 1.055× 10^{-34} Js$ is Planck’s constant. $c = 2.998× 10^{8}$ ms^-¹ is the speed of light.

Fig. 1Schematic of an electrically actuated nano-beam

Dimensionless variables are now introduced:

2

u = \frac{w}{g}, z = \frac{x}{l}, t = t^{'} \frac{1}{l^{2}} \sqrt{\frac{E I}{ρ A}},

where $u$ , $z$ , and $t$ are the dimensionless displacement of beam, dimensionless longitudinal coordinate, and dimensionless time, respectively. The dimensionless equation of the motion and boundary conditions are written as:

3

\frac{\partial^{2} u}{\partial t^{2}} + u^{″ ″} = β \int_{0}^{l} {u^{'}}^{2} d z u^{″} - b \frac{\partial u}{\partial t} + \frac{α}{{(1 - u)}^{4}} + \frac{δ}{{(1 - u)}^{2}} V {(t)}^{2} + f \frac{δ}{(1 - u)} V {(t)}^{2} .

For a simply-simply supported (S-S) nano-beam:

4

u (0, t') = u^{″} (0, t') = u (1, t') = u^{″} (1, t') = 0 .

For a clamped-clamped supported (C-C) nano-beam:

5

u (0, t') = u^{'} (0, t') = u (1, t') = u^{'} (1, t') = 0,

where:

α = \frac{π^{2} ℏ c W l^{4}}{240 g^{5} E I}, δ = \frac{ε_{0} W l^{4}}{2 g^{3} E I} V_{0}^{2}, f = \frac{0.65 g}{W}, b = \frac{b^{*} l^{2}}{\sqrt{ρ A E I}}, β = \frac{A g^{2}}{2 I}, k = \frac{η l^{4}}{E I} .

Considering $α$ , $δ$ , $β$ , $f$ and $b$ to be small parameters, the influences of the Casimir effect, excitation force, fringe correction, and damping are taken as weak terms. Expanding around $u =$ 0 of the right-hand side of Eq. (3), retaining the terms up to the third power of $u$ , and setting all these terms to a slow scale by multiplying them by $ε$ a small dimensionless bookkeeping parameter, one obtains:

6

\frac{\partial^{2} u}{\partial t^{2}} + u^{″ ″} = ε β \int_{0}^{l} {u^{'}}^{2} d z u^{″} - ε b \frac{\partial u}{\partial t} + ε α [1 + 4 u + 10 u^{2} + 20 u^{3}]

+ ε δ [(1 + f) + (2 + f) u + (3 + f) u^{2} + (4 + f) u^{3}] V^{2} (t) .

A first-order expansion of the dimensionless displacement $u$ can be written as:

7

u (z, r, ε) = u_{0} (z, T_{0}, T_{1}) + ε u_{1} (z, T_{0}, T_{1}) + \dots,

where $T_{0} = t$ is a fast time scale and $T_{1} = ε t$ is a slow time scale. Substituting Eq. (7) and the time derivatives into Eq. (6) and equating coefficients of like powers of $ε,$ the following approximation equations and boundary conditions are written as:

8

D_{0}^{2} u_{0} + \frac{\partial^{4} u_{0}}{\partial z^{4}} = 0 .

For the simply-simply supported nano-beam:

9

u_{0} (0, t) = {u^{″}}_{0} (0, t) = u_{0} (1, t) = {u^{″}}_{0} (1, t) = 0 .

For the clamped-clamped supported nano-beam:

10

u_{0} (0, t) = {u^{'}}_{0} (0, t) = u_{0} (1, t) = {u^{'}}_{0} (1, t) = 0,

11

D_{0}^{2} u_{1} + \frac{\partial^{4} u_{1}}{\partial z^{4}} = - 2 D_{0} D_{1} u_{0} - b D_{0} u_{0} + β \int_{0}^{l} {u^{'}}_{0}^{2} d z {u^{″}}_{0}^{2} + α [1 + 4 u + 10 u_{0}^{2} + 20 u_{0}^{3}]

+ δ [(1 + f) + (2 + f) u_{0} + (3 + f) u_{0}^{2} + (4 + f) u_{0}^{3}] V^{2} (T_{0}) .

For the simply-simply supported nano-beam:

12

u_{1} (0, t) = {u^{″}}_{1} (0, t) = u_{1} (1, t) = {u^{″}}_{1} (1, t) = 0 .

For the clamped-clamped supported nano-beam:

13

u_{1} (0, t) = {u^{'}}_{0} (0, t) = u_{1} (1, t) = {u^{'}}_{1} (1, t) = 0,

where $D_{n} = \partial / \partial T_{n}$ , $n =$ 0, 1, 2,…. The first order approximate solution of Eq. (8) can be written as:

14

u_{0} (z, T_{0}, T) = ϕ_{k} (z) [A_{k} (T) e^{i ω_{k} T_{0}} + {\bar{A}}_{k} (T_{1}) e^{- i ω_{k} T_{0}}] .

The dimensionless voltage is considered as [17]:

15

V (τ) = c o s Ω_{}^{*} T_{0},

where $Ω_{}^{*}$ is the dimensionless frequency of excitation given by:

16

Ω^{*} = Ω l^{2} \sqrt{\frac{ρ A}{E I}} .

The resonance when excitation frequency is near half the natural frequency is investigated. The excitation frequency can be written as:

17

2 Ω^{*} = ω_{k} + ε σ,

where $σ$ is a detuning parameter. The square of the voltage $V$ is given by [17]:

18

V^{2} (T_{0}) = \frac{1}{2} + \frac{(e^{i ω_{k} T_{0} + i σ T_{1}} + e^{- i ω_{k} T_{0} - i σ T_{1}})}{4} .

Substituting Eqs. (14) and (18) into Eq. (11), the secular terms are collected and set equal to zero. One can notice that there are additional secular terms for the excitation frequencies near-half natural frequency. By using the solvability condition and stating that the right-hand side to be orthogonal to every solution of the homogenous problem Eq. (11), one obtains:

19

- 2 i ω k g_{1 k k} D_{1} A_{k} - i ω_{k} b g_{1 k k} A_{k} + (4 α + C_{2}) g_{1 k k} A_{k} + 3 (20 α + C_{4}) g_{3 k k} A_{k}^{2} {\bar{A}}_{k}

+ 3 β g_{4 k k} A_{k}^{2} {\bar{A}}_{k} + \frac{1}{2} C_{1} g_{0 k k} e^{i σ T_{1}} + C_{3} g_{2 k k} A_{k} {A^{'}}_{k} e^{i σ T_{1}} + \frac{1}{2} C_{3} g_{2 k k} A_{k}^{2} e^{i σ T_{1}} = 0,

where:

C_{i} = \frac{1}{2} (i + f) δ, i = 1, 2, 3, 4, g_{n k k} = \int_{0}^{1} ϕ_{k}^{n} ϕ_{k} d z, n = 0, 1, 2, 3,

g_{4 k k} = \int_{0}^{1} {ϕ^{″}}_{k} ϕ_{k} d z \int_{0}^{1} {ϕ^{'}}_{k}^{2} d z .

Expressing $A_{k}$ in polar form:

20

A_{k} = \frac{1}{2} a e^{i β_{k}} .

Separating the real and imaginary parts of the equation of the secular terms, the amplitude $a_{k}$ and phase $γ_{k}$ of the response is governed by the following polar form of modulation equations:

21

D_{1} a_{k} = - μ_{k} a_{k} + (ς_{k} a_{k}^{2} + F_{k}) s i n (γ_{k}),

22

a_{k} D_{1} γ_{k} = σ_{k} a_{k} + v_{k} a_{k}^{3} + (ς_{k} a_{k}^{2} + F_{k}) c o s (γ_{k}), γ_{k} = σ T_{1} - β_{k},

where:

μ_{k} = \frac{b}{2 ω_{k}}, ς_{k} = \frac{C_{3} g_{2 k k}}{8 ω_{k} g_{1 k k}}, F_{k} = \frac{C_{1} g_{0 k k}}{2 ω_{k} g_{1 k k}},

v_{k} = \frac{3 (20 α + C_{4}) g_{3 k k} + 3 β g_{4 k k}}{8 ω_{k} g_{1 k k}}, σ_{k} = \frac{(2 ω_{k} σ + 4 α + C_{2})}{2 ω_{k}} .

Steady state solutions of Eq. (1) for the primary resonance response correspond to the fixed points of Eqs. (21) and (22), which can be obtained by setting $D_{1} a_{k} = D_{1} γ_{k} = 0$ . That is:

23

- μ_{k} a_{k} + (ς_{k} a_{k}^{2} + F_{k}) s i n (γ_{k}) = 0,

24

σ_{k} a_{k} + v_{k} a_{k}^{3} + (ς_{k} a_{k}^{2} + F_{k}) c o s (γ_{k}) = 0 .

From Eqs. (23) and (24), the frequency-response equation is obtained:

25

{(μ_{k} a_{k})}^{2} + {(σ_{k} a_{k} + v_{k} a_{k}^{3})}^{2} = {(ς_{k} a_{k}^{2} + F_{k})}^{2} .

The amplitude of the response is functions of the external detuning and the amplitude of the excitation.

Let $E_{k} = a_{k}^{2}$ , Eq. (25) can be written as:

26

E_{k}^{3} + \frac{2 σ_{k} v_{k} - ς_{k}^{2}}{v_{k}^{2}} E_{k}^{2} + \frac{v_{k}^{2} + σ_{k}^{2} - 2 ς_{k}^{} F_{k}}{v_{k}^{2}} E_{k}^{} - \frac{F_{k}^{2}}{v_{k}^{2}} = 0 .

The derivative of Eq. (25) with respect to $σ$ yields [20]:

27

\frac{\partial E_{k}^{}}{\partial σ} = - \frac{2 v_{k} E_{k}^{2} + 2 σ_{k} E_{k}^{}}{3 E_{k}^{2} v_{k}^{2} + 2 E_{k} (2 σ_{k} v_{k} - ς_{k}^{2}) + v_{k}^{2} + σ_{k}^{2} - 2 ς_{k}^{} F_{k}} .

Along the resonance curve, we consider the peak of the resonance. At this point, with the drive held fixed:

28

\frac{\partial E_{k}^{}}{\partial σ} = 0 .

This implies that at the peak of the resonance:

29

v_{k} E_{k}^{} + σ_{k} = 0 .

Substituting this equation into Eq. (24), one can finds that $c o s (γ_{k}) =$ 0. Assumed that $ς_{k} a_{k}^{2} + F_{k} \neq 0$ , one yields:

30

ς_{k} a_{k m a x}^{2} - μ_{k} a_{k m a x} + F_{k} = 0 .

Then, the peak amplitude of the primary resonance $a_{k m a x}$ can be written as:

31

a_{k m a x} = \frac{μ_{k} \pm \sqrt{μ_{k}^{2} - 4 ς_{k} F_{k}}}{2 ς_{k}} .

The peak amplitude of the primary resonance is functions of the damping, the external detuning and the amplitude of the excitation.

The stability of the solutions is determined by the eigenvalues of the corresponding Jacobian matrix of Eq. (6). The corresponding eigenvalues are the roots of:

32

λ^{2} + m_{k} λ + n_{k} = 0,

where:

m_{k} = \frac{2 F_{k} μ_{k}}{ς_{k} a_{k}^{2} + F_{k}},

n_{k} = \frac{F_{k} - ς_{k} a_{k}^{2}}{ς_{k} a_{k}^{2} + F_{k}} μ_{k}^{2} + \frac{σ_{k} + v_{k} a_{k}^{2}}{ς_{k} a_{k}^{2} + F_{k}} (v_{k} ς_{k} a_{k}^{4} + F_{k} σ_{k} + 3 v_{k} a_{k}^{2} F_{k} - σ_{k} ς_{k} a_{k}^{2}) .

The sum of the two eigenvalues is – $m_{k}$ . If $m_{k} <$ 0, it means at least one of the eigenvalues will always have a positive real part. The system will be unstable. If $m_{k} =$ 0, it means a pair of purely imaginary eigenvalues and hence a Hopf bifurcation may occur. If $m_{k} >$ 0, the sum of two eigenvalues is always negative, and accordingly, at least one of the two eigenvalues will always have a negative real part. Based on the analyses mentioned above, the sufficient conditions of guaranteeing the system stability are [14]:

33

f (σ_{k}) = n_{k} > 0, m_{k} > 0 .

Unstable periodic solutions corresponding to a saddle is:

34

f (σ_{k}) = n_{k} < 0 .

The value of $f (σ_{k})$ is positive value when there is no solution of equation $f (σ_{k}) = 0$ :

35

f (σ_{k}) = n_{k} = 0,

where a saddle-node bifurcation occurs.

3. Case study

The behavior of an electrostatically actuated simply-simply and clamped-clamped supported nano-beam is investigated. The nano-beam is modeled as an Euler-Bernoulli. Table 1 gives the common boundary conditions for the transverse vibration of beams.

The nonlinearities arise from the large deformation of structure is considered. The electrostatic and Casimir forces acting on the resonator induce nonlinear resonances. Parametric coefficients are found in both linear and nonlinear terms within the governing equation. The model also includes first-order fringe correction of the electrostatic field. The case of uniform beams is considered. Table 2 gives values of the physical characteristics of a typical nano-beam.

Nonlinearities play a significant role in nano scale. In the work, the nonlinearities arise from a number of sources such as large deflections, electrostatic actuation, and Casimir effect. As the excitation magnitude increases, nano-beam resonators display distinctive nonlinear characteristics due to the relatively small dimensions of nano-beam. Electrostatic actuation can create a variety of nonlinear parametric resonances depending on system parameters, excitation frequency, and excitation voltage. When the separation of surfaces is larger than 20 Nm and less than 1000 Nm, Casimir effects occur [21]. In this work, such gap distances are considered. The influence of the large deflections, electrostatic actuation, and Casimir effect to the nonlinear terms is relative to the distance between the nano-beam and the substrate. Tables 3 and 4 shows comparison of the value of the nonlinear terms among the Casimir effect, electrostatic actuation, and large defections of the S-S and C-C beam. There are small changes for the values of nonlinear terms of the Casimir effect and electrostatic actuation when the gap between the nano-beam and the substrate becomes large. However, the nonlinear term induced by the large deformation changes on the contrary.

Table 1Common boundary conditions for the transverse vibration of beams

End conditions of beam	Mode shape	Value of $ξ$
Simply-simply supported	$s i n (\frac{ξ}{l} x)$	$π$
Clamped-clamped supported	$[c o s h (\frac{ξ}{l} x) - c o s (\frac{ξ}{l} x)] - υ [c o s h (\frac{ξ}{l} x) - c o s (\frac{ξ}{l} x)]$	4.730
where $υ = \frac{c o s h ξ - c o s ξ}{s i n h ξ - s i n ξ} .$

Table 2Physical characteristics of a nanobeam

Parameter	Symbol	Value
Beam width	$W$	500 Nm
Beam length	$l$	30 μm
Beam thickness	$h$	300 Nm
Initial gap distance	$g$	200 Nm
Material density	$ρ$	‎2330 kg/m³‎
Young’s modulus	$E$	169 GPa
Peak AC voltage	$V$	2.0 V

Table 3Comparison of the value of nonlinear terms among the Casimir effect, electrostatic actuation and large deformation of the first mode of S-S beam

$g$ , Nm	Casimir effect	Electrostatic actuation	Large deformation
50.0000	10.1063	17.4783	–0.6169
70.0000	1.8791	6.4104	–1.2090
90.0000	0.5348	3.0353	–1.9986
110.0000	0.1961	1.6730	–2.9856
130.0000	0.0851	1.0199	–4.1699
150.0000	0.0416	0.6680	–5.5517
170.0000	0.0222	0.4618	–7.1308
190.0000	0.0128	0.3328	–8.9073
210.0000	0.0077	0.2480	–10.8813

Fig. 2 shows the primary resonance curves of the first mode of simply-simply supported nano-beam for three different sets of the excitation voltages. There is no jump and hysteresis phenomenon when $V_{0} =$ 1.5 V. The saddle node bifurcation and jump phenomenon can be eliminated by choosing certain numerical values of the excitation voltages. Three solutions exist in the cases of $V_{0} =$ 2.0 V and $V_{0} =$ 2.1 V. The jump phenomenon presents. The peak amplitude of the primary resonance response at $V_{0} =$ 1.5 V is the smallest one among the three cases.

Fig. 3 shows the primary resonance curves of the first mode of simply-simply supported nano-beam for considering the effect of the nonlinear term or not. There is no jump and hysteresis phenomenon when the effect of the nonlinear term is $β =$ 0. Three solutions exist in the cases of considering the effect of the nonlinear term $β =$ 2.6667. The jump phenomenon presents. There is a different vibration behavior for the nonlinear vibration of the nonlinear system. So, the effect of the nonlinear term to the vibration behavior should be taken into account in the analysis of the large deformation of the nano-beam.

Table 4Comparison of the value of nonlinear terms among the Casimir effect, electrostatic actuation, and large deformation of the first mode of C-C beam

$g$ , Nm	Casimir effect	Electrostatic actuation	Large deformation
50.0000	9.8517	17.0380	–0.7568
70.0000	1.8318	6.2489	–1.4832
90.0000	0.5214	2.9588	–2.4519
110.0000	0.1912	1.6308	–3.6627
130.0000	0.0829	0.9942	–5.1157
150.0000	0.0405	0.6512	–6.8108
170.0000	0.0217	0.4501	–8.7481
190.0000	0.0124	0.3244	–10.9276
210.0000	0.0075	0.2417	–13.3492

Fig. 2Amplitude-frequency of primary resonance curves of the first mode of simply-simply supported nano-beam for three different sets of the excitation voltages

Amplitude-frequency of primary resonance curves of the first mode of simply-simply supported nano-beam for three different sets of the excitation voltages

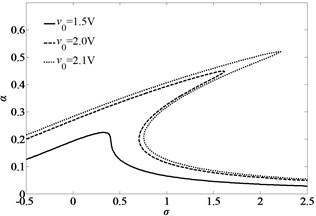
Fig. 3Amplitude-frequency curves of primary resonance of the first mode of simply-simply supported nano-beam for considering the nonlinear term of large deformation or not

Amplitude-frequency curves of primary resonance of the first mode of simply-simply supported nano-beam for considering the nonlinear term of large deformation or not

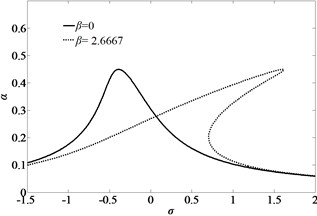
Fig. 4Critical curve of saddle burfurcation of the simply-simply supported nano-beam

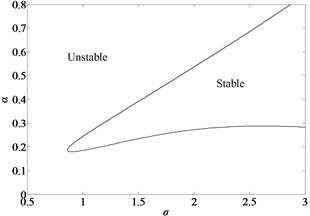
Fig. 5Jump curves of the simply-simply supported nano-beam

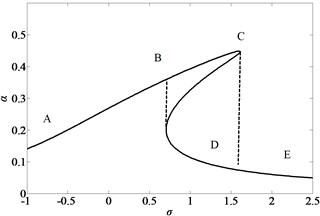
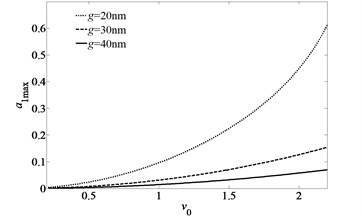
Fig. 6Peak amplitude of the primary resonance curves of the first mode of simply-simply supported nano-beam for three different sets of the initial gap between the beam and ground electrode

Peak amplitude of the primary resonance curves of the first mode of simply-simply supported nano-beam for three different sets of the initial gap between the beam and ground electrode

The sum of the two eigenvalues is always negative when $m_{k} >$ 0, and accordingly, one of the two eigenvalues must have at least a negative real part. When $f (σ_{k}) = 0$ , the other eigenvalue is zero where a saddle-node bifurcation occurs. We utilize Eq. (35) to study variation of the response amplitude with the excitation voltage. The critical curve of saddle burfurcation of the simply-simply supported nano-beam is illustrated in Fig. 4. When $n_{k} >$ 0, the vibration system may be stable. However, When $n_{k} <$ 0, the vibration system is unstable. Stable and unstable regions are shown in the figure.

The variation of the response amplitude with the frequency detuning parameter $σ$ and the excitation amplitude is studied by utilizing Eq. (25). Fig. 5 illustrates the frequency-response curve of the simply-simply supported nano-beam when $σ_{A} < σ_{B}$ , which only a stable trivial solution exists. As $σ$ is increased, the trivial solution loses stability at point C and gives rise to a branch of stable periodic solutions. The amplitude of these stable solutions increases as $σ$ is increased further towards point C. At point C, the periodic solution loses stability through a saddle-node bifurcation, and the response amplitude jumps down to point D where only trivial solutions exist. Increasing beyond point D leads only to the stable trivial solutions.

Fig. 6 shows the peak amplitude of the primary resonance curves of the first mode of simply-simply supported nano-beam for three different sets of the initial gap between the beam and ground electrode. It is easily noted that $a_{m a x}$ decreases significantly as the initial gap between the beam and ground electrode increases. A larger initial gap can relatively lead to a smaller peak amplitude $a_{m a x}$ . For fixed initial gap, the increase of the excited voltage can lead to the increase of the peak amplitude.

4. Conclusions

The nonlinear response of electrostatically actuated nano-beam near-half natural frequency is studied by considering the nonlinearities of the large deformation, electrostatic force and Casimir effect. The gap between the nano-beam and the substrate decides the values of the nonlinear terms of the Casimir effect, electrostatic actuation and large deformation. The gap distances have the different influence on the value of large deflections, electrostatic actuation, and Casimir effect. The peak amplitude decreases with the increasing of the gap distances and increases with the largening of the excited voltage. Some references are given for the analysis and control of the nano and micro nonlinear system.

The sufficient conditions guaranteeing the system stability is given. The saddle-node bifurcation is studied. The nonlinearities of large deformation, damping, actuation, and fringe effect have influences on the resonator response. The peak amplitude of the primary resonance has a relationship to the damping, the external detuning and the amplitude of the excitation.

References

Burg T. P., Mirza A. R., Milovic N., et al. Vacuum-packaged suspended microchannel resonant mass sensor for biomolecular detection. Journal of Microelectromechanical Systems, Vol. 15, Issue 6, 2006, p. 1466-1476.

Search CrossRef
Zhang W. H., Turner K. L. Application of parametric resonance amplification in a single-crystal silicon micro-oscillator based mass sensor. Sensors and Actuators A: Physical, Vol. 122, Issue 1, 2005, p. 23-30.

Search CrossRef
Yabuno H., Kaneko H. Van der Pol type self-excited micro-cantilever probe of atomic force microscopy. Nonlinear Dynamics, Vol. 54, Issue 1-2, 2008, p. 137-149.

Search CrossRef
Nayfeh A. H., Younis M. I. Dynamics of MEMS resonators under superharmonic and subharmonic excitations. Journal of Micromechanics and Microengineering, Vol. 15, Issue 10, 2005, p. 1840-1847.

Search CrossRef
Nayfeh A. H., Younis M. I., Abdel-Rahman E. M. Dynamic pull-in phenomenon in MEMS resonantors. Nonlinear Dynamics, Vol. 48, Issue 1-2, 2007, p. 153-163.

Search CrossRef
Younis M. I., Nayfeh A. H. A study of the nonlinear response of a resonant microbeam to an electric actuation. Nonlinear Dynamics, Vol. 31, Issue 1, 2003, p. 91-117.

Search CrossRef
Kim B., Hopcroft M., Jha C. M., et al. Using MEMS to build the device and the package. Transducers Eurosensors, Lyon, France, 2007.

Search CrossRef
Kim B., Hopcroft M. A., Melamud R., et al. CMOS Compatible wafer-scale encapsulation with MEMS Resonators. ASME InterPACK, Vancouver, Canada, 2007.

Search CrossRef
Jha C. M., Hopcroft M. A., Chandorkar S. A., et al. Thermal isolation of encapsulated MEMS resonators. Journal of Microelectromechanical Systems, Vol. 17, Issue 1, 2008, p. 175-184.

Search CrossRef
Younis M. I., Nayfeh A. H. A study of the nonlinear response of a resonant microbeam to an electric actuation. Nonlinear Dynamics, Vol. 31, Issue 1, 2003, p. 91-117.

Search CrossRef
Mestrom R. M. C., Fey R. H. B., et al. Modelling the dynamics of a MEMS resonator: simulations and experiments. Sensors and Actuators A: Physical, Vol. 142, Issue 1, 2008, p. 306-315.

Search CrossRef
Postma H. W. Ch., Kozinsky I., Husain A., et al. Dynamic range of nano-tube and nanowire-based electromechanical systems. Applied Physics Letters, Vol. 86, Issue 22, 2005, p. 223105.

Search CrossRef
Conley W. G., Raman A., Krousgrill C. M., et al. Nonlinear and nonplanar dynamics of suspended nano-tube and nanowire resonators. Nano Letters, Vol. 8, Issue 6, 2008, p. 1590-1595.

Search CrossRef
Rhoads J. F., Shaw S. W., Turner K. L., et al. Generalized parametric resonance in electrostatically actuated microelectromechanical oscillators. Journal of Sound and Vibration, Vol. 296, 2006, p. 797-829.

Search CrossRef
DeMartini B. E., Butterfield H. E., Moehlis J., et al. Chaos for a microelectromechanical oscillator governed by the nonlinear mathieu equation. Journal of Microelectromechanical Systems, Vol. 16, Issue 6, 2007, p. 1314-1323.

Search CrossRef
Ke Changkong Resonant pull-in of a double-sided driven nanotube-based electromechanical resonator. Journal of Applied Physics, Vol. 105, Issue 2, 2009, p. 1-8.

Search CrossRef
Caruntu D. I., Knecht M. W. On nonlinear response near half natural frequency of electrostatically actuated microresonators. International Journal of Structural Stability and Dynamics, Vol. 11, Issue 4, 2011, p. 641-672.

Search CrossRef
Palevicius P., Ragulskis M., Palevicius A., et al. Applicability of time-averaged holography for micro-electro-mechanical system performing non-Linear oscillations. Sensors, Vol. 14, 2014, p. 1805-1821.

Search CrossRef
Kilho Eom, Harold S. Park, Dae Sung Yoon, et al. Nanomechanical resonators and their applications in biological/chemical detection: Nanomechanics principles. Physics Reports, Vol. 503, 2011, p. 115-163.

Search CrossRef
Yurke B., Greywall D. S., Pargellis A. N.,et al. Theory of amplifier-noise evasion in an oscillator employing a nonlinear resonator. Physical Review A, Vol. 51, 1995, p. 4211-4229.

Search CrossRef
Lamoreaux S. K. The Casimir force: background, experiments, and applications. Reports on the Progress of Physics, Vol. 68, 2005, p. 201-236.

Search CrossRef

About this article

Received

23 October 2013

Accepted

07 June 2014

Published

15 August 2014

Keywords

nano-beam

nonlinear vibration

Casimir effect

electrostatic force

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.