Effects of Casimir force on multi-field coupled nonlinear vibration of orthotropic micro film

In this paper, the nonlinear dynamics equations of a multi-field coupled orthotropic micro film are presented. The Krylov-Bogoliubov-Mitropolsky (KBM) method is used to solve the equations. The multi-fields coupled nonlinear resonant frequencies of a micro film are analyzed. The effects of Casimir force and nonlinear parameter on nonlinear resonant frequencies and vibration amplitudes are investigated. A resonant film is designed and produced. Based on the principle of electrostatic excitation and capacitance detection, the resonant frequency of the micro film is detected. It illustrates that the Casimir force has an important influence on the resonant micro film frequencies and should be considered with a small initial clearance.

1. Introduction

Micro-electro-mechanical systems (MEMS) mainly include micro-sensors, micro-actuators and processing circuits [1, 2]. As an important branch of MEMS devices, micro-sensors have advantages such as fast responses, high sensitivity, and are suitable for mass production, etc. [3]. Among the micro-sensors, resonant sensors output frequency signals in which the distortion will not occur in the long-distance transmission, and the signal processing circuits can be simplified largely so that they are widely used in automobile, intelligent equipment, chemical industry, quality and process control, fragrance design, oenology, etc [4]. Resonant sensor resonator mainly includes two types: film or beam. The beam resonator has a higher sensitivity than a film resonator, but its output signals are weaker, and a higher precise detection circuit is required. The output signal of the film resonant sensor is strong, and the requirement to a test circuit is low, of course, its sensitivity is lower than that of beam resonators [5, 6].

Micro resonant sensors work in the resonant state. Physical quantities are detected by fluctuations of the resonant frequencies. So, for a micro sensor with film resonator, determining the resonant frequency and its fluctuations along with the system parameters is an important problem. For the dynamics problem of the micro film, a lot of studies have been done.

The film vibration theory was derived from the string vibration theory in the 18th century [7]. In 1993, Alonso studied the vibration characteristics for a resonator made with NiCr thin film micro resonance pressure sensor [8]. Fan studied the nonlinear vibration of a micro resonant pressure sensor. The multi-scale method was used to analyze the influence of the nonlinear term on the natural frequency of the sensor [9]. Federico discussed the Casimir effect and its use in nanomechanics and nanotechnology, and finished high precision measurements of the Casimir force using microelectromechanical systems technology [10]. In 2009, Reutskiy developed a new method of numerical analysis of the nonlinear film vibration. This method is based on a mathematical simulation of the physical response of the spectrum analysis system [11]. In the same year, Goncalves analyzed the geometrical and material nonlinear vibrations of hyperelastic tensioned films under small deformation and time-dependent transverse pressure by the method of Galerkin [12]. Liu carried out a theoretical analysis of the nonlinear free vibration of thin films and the forced vibrations under impact loads [13]. The dynamics of a circular film in zero gravity was studied by Sorokin, and the spectrum of natural vibrations were given [14].

J Weber studied thin film resonators as environmental pressure sensors and developed a model to evaluate their sensitivity [15]. Steffen developed a polycrystalline silicon thin film resonator with three-layer or two-layer structure, different film strain factors, and different resistance temperature coefficients [16]. Zhao fabricated an odorant biosensor based on ZnO film bulk acoustic resonators (FBARs) with resonant frequency of –1.5 GHz, and demonstrated the potential of FBARs as odorant biosensors [17]. Jiang fabricated high-performance PZT thin films with a thickness of 2.6 μm which are produced on a silicon substrate by the sputtering deposition process, and a Lamb wave resonator was fabricated using the highly selective reactive ion etching process [18]. Gualdino fabricated a thin-film silicon resonator by surface micromachining and studied vibration modes of micromechanical disk resonators made of hydrogenated amorphous silicon films [19]. Ren presented a novel resonant pressure sensor with an improved micromechanical double-ended tuning fork resonator packaged in dry air at the atmospheric pressure in which the fundamental frequency of the resonant pressure sensor is approximately 34.55 kHz with a pressure sensitivity of 20.77 Hz/kPa [20]. Hamelin studied a new method to optically trim the resonance frequency of micro-silicon resonator coated with a film germanium layer [21]. Alahnomi developed a new sensor for detecting the properties of the materials [22].

However, the resonator of a resonant sensor operates normally under multi-fields forces. Especially, as the resonator size reduces, effects of the molecule force on its resonant frequency become more significant and could not be neglected. To predict the resonant frequency and its fluctuations of the micro film resonator accurately, the multi-field coupled vibration problem under the influence of molecular force should be investigated.

In this paper, a multi-field coupled dynamics model of the orthotropic film resonator is proposed. Here, the Casimir force, the air damping force and the electrostatic force are considered. Using the model, the nonlinear vibration frequency and displacement response of the micro film resonator are investigated. Effects of the Casimir force on the nonlinear vibration frequency for the micro film resonator are determined. To illustrate the analysis, a micro film resonator is fabricated, and the nonlinear frequencies of the resonator under different initial clearances are detected. Results show that the detected resonant frequencies are in agreement with the calculative values. The results can be used in design of the resonant frequencies for a micro resonant film sensor. A flowchart of the research idea is given in Fig. 1.

Fig. 1Research idea flowchart

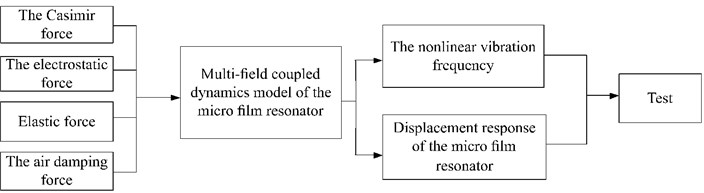
2. Coupled dynamics equations

An orthotropic resonant film in the micro resonant sensor is shown in Fig. 2. This is a multi-field coupled system for the micro-thin film under the action of electrostatic force, Casimir force and air damping force. Its boundary condition is that two sides are fixed and two sides are free. Here, $h$ is the film thickness, $Δ w$ is the film vibration displacement, $a$ and $b$ are the resonant film dimensions, $v$ is the initial clearance between the film and base plate.

According to the theory of D’Alembert principle [23], the control equations of nonlinear free vibration for the film are given by:

1

ρ h \frac{\partial^{2} Δ w}{\partial t^{2}} + γ \frac{\partial Δ w}{\partial t} - (σ_{x 0} + \frac{\partial^{2} φ}{\partial y^{2}}) h \frac{\partial^{2} Δ w}{\partial x^{2}} - (σ_{y 0} + \frac{\partial^{2} φ}{\partial x^{2}}) h \frac{\partial^{2} Δ w}{\partial y^{2}} = Δ q,

2

\frac{1}{E_{1}} \frac{\partial^{4} φ}{\partial y^{4}} + \frac{1}{E_{2}} \frac{\partial^{4} φ}{\partial x^{4}} = {(\frac{\partial^{2} Δ w}{\partial x \partial y})}^{2} - \frac{\partial^{2} Δ w}{\partial x^{2}} \frac{\partial^{2} Δ w}{\partial y^{2}},

where $ρ$ is the density, $U_{0}$ is the voltage, $φ$ is the stress function, $σ_{x 0}$ is the initial tension stress in $x$ direction of the film, $σ_{y 0}$ is the initial tension stress in $y$ direction of the film, $E_{1}$ is the Young moduli in x direction, $E_{2}$ is the Young moduli in $y$ direction, $γ$ is the damping coefficient of the air, it can be given as:

3

γ = \frac{μ b^{3}}{{(v - {\bar{w}}_{0})}^{3}},

where $μ$ is the air dynamic viscosity, $μ =$ 1.86×10^-⁵N⋅S·m⁻².

Fig. 2Multi-field coupled dynamics model of micro film resonant sensor

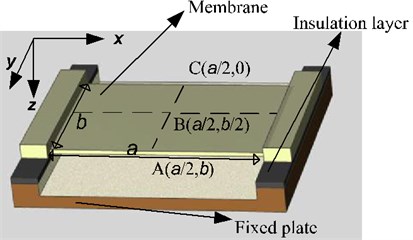
a) Structure model of micro film

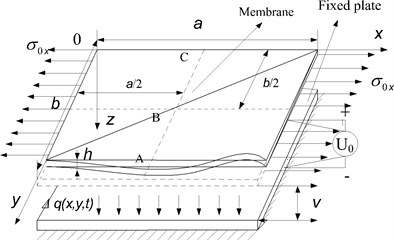
b) Dynamics model of micro film

$Δ q$ is the force per unit area on the film, including the electrostatic force and the Casimir force, it can be given as:

4

Δ q = Δ q_{0} + Δ q_{r} .

From the Lifshitz formula, the Casimir force per unit area is [24]:

5

Δ q_{r} = \frac{π^{2} ℏ c}{240 {(v - w)}^{4}},

where $ℏ$ is the Plank constant divided by 2 $π$ , $ℏ =$ 1.055×10^-34 J·S; $c$ is the light speed, $c =$ 2.998×10⁸ m/s.

Consider the non-linearity of the Casimir force, the Casimir force is written as a Gaussian expansion at the static mean displacement, and letting $ε_{1} = {\bar{w}}_{0} / v$ , ones can obtain:

6

Δ q_{r} = \frac{π^{2} ℏ c}{60 {(v - {\bar{w}}_{0})}^{5}} Δ w + \frac{π^{2} ℏ c ε_{1}}{12 v^{5} {\bar{w}}_{0}} Δ w^{2} + \frac{π^{2} ℏ c ε_{1}}{4 v^{6} {\bar{w}}_{0}} Δ w^{3} + \dots .

The dynamic electrostatic force per unit area due to the film displacement is [25]:

7

Δ q_{0} = \frac{U_{0}^{2} ε_{0}}{{(v - w)}^{3}} \cdot Δ w,

where $ε_{0}$ is the permittivity constant of free space, $ε_{0} =$ 8.85×10^-12 $c$ ²·N^-1·m^-2.

Considering nonlinearity of electrostatic force, the dynamic electrostatic force on the film is written as a Gaussian expansion at the static mean displacement, one obtains

8

Δ q_{0} = \frac{U_{0}^{2} ε_{0}}{{(v - {\bar{w}}_{0})}^{3}} Δ w + \frac{3 U_{0}^{2} ε_{0} ε_{1}}{v^{3} {\bar{w}}_{0}} Δ w^{2} + \frac{6 U_{0}^{2} ε_{0} ε_{1}}{v^{4} {\bar{w}}_{0}} Δ w^{3} + \dots .

Thus, the force per unit area on the film is:

9

Δ q = [\frac{U_{0}^{2} ε_{0}}{{(v - {\bar{w}}_{0})}^{3}} + \frac{π^{2} ℏ c}{60 {(v - {\bar{w}}_{0})}^{5}}] Δ w + [\frac{3 U_{0}^{2} ε_{0}}{v^{3} {\bar{w}}_{0}} + \frac{π^{2} ℏ c}{12 v^{5} {\bar{w}}_{0}}] ε_{1} Δ w^{2} + [\frac{6 U_{0}^{2} ε_{0}}{v^{4} {\bar{w}}_{0}} + \frac{π^{2} ℏ c}{4 v^{6} {\bar{w}}_{0}}] ε_{1} Δ w^{3} .

Substituting Eq. (9) into Eq. (1), one obtains:

10

\begin{array}{l} ρ h \frac{\partial^{2} Δ w}{\partial t^{2}} + γ \frac{\partial w}{\partial t} - (σ_{x 0} + \frac{\partial^{2} φ}{\partial y^{2}}) h \frac{\partial^{2} Δ w}{\partial x^{2}} - (σ_{y 0} + \frac{\partial^{2} φ}{\partial x^{2}}) h \frac{\partial^{2} Δ w}{\partial y^{2}} \\ = [\frac{U_{0}^{2} ε_{0}}{{(v - {\bar{w}}_{0})}^{3}} + \frac{π^{2} ℏ c}{60 {(v - {\bar{w}}_{0})}^{5}}] Δ w + [\frac{3 {U_{0}}^{2} ε_{0}}{v^{3} {\bar{w}}_{0}} + \frac{π^{2} ℏ c}{12 v^{5} {\bar{w}}_{0}}] ε_{1} Δ w^{2} \\ + [\frac{6 {U_{0}}^{2} ε_{0}}{v^{4} {\bar{w}}_{0}} + \frac{π^{2} ℏ c}{4 v^{6} {\bar{w}}_{0}}] ε_{1} Δ w^{3} . \end{array}

For the boundary conditions, the solutions of Eqs. (1) and (2) can be given as [26]:

11

Δ w (x, y, t) = W (x, y) T (t),

12

φ (x, y, t) = ϕ (x, y) T^{2} (t),

13

W (x, y) = s i n \frac{m π x}{a} c o s \frac{n π y}{b} .

Thus:

14

Δ w (x, y) = s i n \frac{m π x}{a} c o s \frac{n π y}{b} T (t) .

Substituting Eqs. (12) and (14) into Eq. (2), one yields:

15

\frac{1}{E_{1}} \frac{\partial^{4} ϕ}{\partial y^{4}} + \frac{1}{E_{2}} \frac{\partial^{4} ϕ}{\partial x^{4}} = \frac{m^{2} n^{2} π^{4}}{2 a^{2} b^{2}} (c o s \frac{2 m π x}{a} - c o s \frac{2 n π y}{b}) .

Let:

16

ϕ (x, y) = α c o s \frac{2 m π x}{a} - β c o s \frac{2 n π y}{b} .

Substituting it into Eq. (15), one yields the following equations:

17

α = \frac{E_{2} n^{2} a^{2}}{32 m^{2} b {}^{2}}, β = \frac{E_{1} m^{2} b^{2}}{32 n^{2} a {}^{2}} .

Substituting Eq. (17) into Eq. (12), one yields:

18

φ (x, y, t) = (\frac{E_{2} n^{2} a^{2}}{32 m^{2} b {}^{2}} c o s \frac{2 m π x}{a} - \frac{E_{1} m^{2} b^{2}}{32 n^{2} a {}^{2}} c o s \frac{2 n π y}{b}) T^{2} (t) .

The substitution of Eqs. (14) and (18) into Eq. (1) and using the Galerkin method [27], one obtains:

19

\iint [ρ h \frac{\partial^{2} Δ w}{\partial t^{2}} + γ \frac{\partial Δ w}{\partial t} - (σ_{0 x} + \frac{\partial^{2} φ}{\partial y^{2}}) h \frac{\partial^{2} w}{\partial x^{2}} - (σ_{0 y} + \frac{\partial^{2} φ}{\partial x^{2}}) h \frac{\partial^{2} Δ w}{\partial y^{2}}]

∙ s i n \frac{m π x}{a} c o s \frac{n π y}{b} d x d y = \iint \{[\frac{{U_{0}}^{2} ε_{0}}{{(v - {\bar{w}}_{0})}^{3}} + \frac{π^{2} ℏ c}{60 {(v - {\bar{w}}_{0})}^{5}}] Δ w + [\frac{3 {U_{0}}^{2} ε_{0}}{v^{3} {\bar{w}}_{0}} + \frac{π^{2} ℏ c}{12 v^{5} {\bar{w}}_{0}}] ε_{1} Δ w^{2} + [\frac{6 {U_{0}}^{2} ε_{0}}{v^{4} {\bar{w}}_{0}} + \frac{π^{2} ℏ c}{4 v^{6} {\bar{w}}_{0}}] ε_{1} Δ w^{3}\} s i n \frac{m π x}{a} c o s \frac{n π y}{b} d x d y .

Let it be that:

20a

S_{111} = \iint ρ h s i n^{2} \frac{m π x}{a} c o s^{2} \frac{n π y}{b} d x d y = \frac{ρ h a b}{4},

20b

S_{222} = \iint γ s i n^{2} \frac{m π x}{a} c o s^{2} \frac{n π y}{b} d x d y = \frac{γ a b}{4},

20c

S_{333} = \iint (σ_{0 x} \frac{\partial^{2} W}{\partial x^{2}} + σ_{0 y} \frac{\partial^{2} W}{\partial y^{2}}) h s i n \frac{m π x}{a} c o s \frac{n π y}{b} d x d y = - \frac{π^{2} a b h}{4} (\frac{m^{2}}{a^{2}} σ_{0 x} + \frac{n^{2}}{b^{2}} σ_{0 y}),

20d

S_{444} = \iint (\frac{\partial^{2} ϕ}{\partial y^{2}} \frac{\partial^{2} W}{\partial x^{2}} + \frac{\partial^{2} ϕ}{\partial x^{2}} \frac{\partial^{2} W}{\partial y^{2}}) h s i n \frac{m π x}{a} c o s \frac{n π y}{b} d x d y = \frac{3 π^{4} a b h}{64} (\frac{E_{1} m^{4}}{a^{4}} - \frac{E_{2} n^{4}}{b^{4}}),

20e

S_{555} = \iint [\frac{{U_{0}}^{2} ε_{0}}{{(v - {\bar{w}}_{0})}^{3}} + \frac{π^{2} ℏ c}{60 {(v - {\bar{w}}_{0})}^{5}}] s i n^{2} \frac{m π x}{a} c o s^{2} \frac{n π y}{b} d x d y = \frac{{U_{0}}^{2} ε_{0} a b}{4 {(v - {\bar{w}}_{0})}^{3}} + \frac{π^{2} ℏ c a b}{240 {(v - {\bar{w}}_{0})}^{5}},

20f

S_{666} = \iint (\frac{6 {U_{0}}^{2} ε_{0}}{v^{4} {\bar{w}}_{0}} + \frac{π^{2} ℏ c}{4 v^{6} {\bar{w}}_{0}}) ε_{1} s i n^{3} \frac{m π x}{a} c o s^{3} \frac{n π y}{b} d x d y = 0,

20g

S_{777} = \iint (\frac{6 {U_{0}}^{2} ε_{0}}{v^{4} {\bar{w}}_{0}} + \frac{π^{2} ℏ c}{4 v^{6} {\bar{w}}_{0}}) ε_{1} s i n^{4} \frac{m π x}{a} c o s^{4} \frac{n π y}{b} d x d y = \frac{9 a b ε_{1}}{64} (\frac{6 {U_{0}}^{2} ε_{0}}{v^{4} {\bar{w}}_{0}} + \frac{π^{2} ℏ c}{4 v^{6} {\bar{w}}_{0}}) .

Thus, Eq. (19) can be changed into the following form:

21

S_{111} T^{''} + S_{222} T^{'} - S_{333} T - S_{444} T^{3} = S_{555} T + S_{777} T^{3} .

Utilizing the KBM perturbation method [28], let, $ε_{2} = h^{2} / a b$ and then:

22

T^{''} + \frac{(- S_{333} - S_{555})}{S_{111}} T = ε_{2} (\frac{S_{777} a b}{S_{111} h^{2}} T^{3} + \frac{- S_{222} a b}{S_{111} h^{2}} T^{'}) .

In order to facilitate the calculation, Eq. (22) is converted into following form:

23

T^{''} + {ω_{0}}^{2} T = ε_{2} (ζ_{1} T^{3} + ζ_{2} T^{'}) .

Here:

24a

{ω_{0}}^{2} = \frac{(- S_{333} - S_{555})}{S_{111}},

24b

ζ_{1} = \frac{S_{777} a b}{S_{111} h^{2}},

24c

ζ_{2} = \frac{- S_{222} a b}{S_{111} h^{2}} .

Let it be that:

25

f (T, T') = (ζ_{1} T^{3} + ζ_{2} T'), ϑ = ω_{0} t + η .

Here $η$ is the initial phase of film vibration (let $η =$ 0).

If $ε_{2} =$ 0, Eq. (23) can be changed into following form:

26

\frac{d T}{d t} = - k ω_{0} s i n ϑ .

Consider the influence of non-linearity, ones assume:

27

T = k c o s ϑ + ε T_{1} (k, ϑ) + ε^{2} T_{2} (k, ϑ) + \dots .

Here $k$ and $ϑ$ is the time function, $T_{1}$ and $T_{2}$ is the power series function of $ε$ .

The equivalent damping ratio $δ_{e}$ and the equivalent natural frequency $ω$ of the nonlinear system can be expressed as the form of a small parameter power series:

28

δ_{e} = ε δ_{1} (k) + ε^{2} δ_{2} (k) + \dots,

29

ω = ω_{0} + ε ω_{1} (k) + ε^{2} ω_{2} (k) + \dots .

Utilizing KBM perturbation method (see Appendix), ones obtain:

30

δ_{1} = \frac{ζ_{2}}{2}, ω_{1} = - \frac{3 ζ_{1} k^{2}}{8 ω_{0}},

31

T_{1} = - \frac{ζ_{1} k^{3}}{32 {ω_{0}}^{2}} c o s 3 ϑ,

32

δ_{2} = - \frac{3 ζ_{1} ζ_{2} k^{3}}{16 {ω_{0}}^{2}}, ω_{2} = \frac{3 ζ_{1}^{2} k^{4}}{256 {ω_{0}}^{3}} - \frac{ζ_{2}^{2}}{4 ω_{0}} - \frac{9 ζ_{1}^{2} k^{4}}{128 {ω_{0}}^{3}},

33

T_{2} = \frac{3 ζ_{1}^{2} k^{5}}{512 {ω_{0}}^{4}} c o s 3 ϑ + \frac{3 ζ_{1}^{2} k^{5}}{3072 {ω_{0}}^{4}} c o s 5 ϑ .

From Eq. (29), the non-linear vibration frequency can be obtained:

34

ω = ω_{0} - \frac{3 ε ζ_{1} k_{0}^{2} e^{ε ζ_{2} t}}{8 ω_{0}} - \frac{15 ε^{2} ζ_{1}^{2} {k_{0}}^{4} e^{2 ε ζ_{2} t}}{256 {ω_{0}}^{3}} - \frac{ε^{2} ζ_{2}^{2}}{4 ω_{0}} .

Substituting Eq. (31) and Eq. (33) into Eq. (27), one yields:

35

\begin{array}{l} T = k c o s ϑ + ε T_{1} + ε^{2} T_{2} \\ = k c o s ϑ + (\frac{3 ε^{2} ζ_{1}^{2} k^{5}}{512 {ω_{0}}^{4}} - \frac{ε ζ_{1} k^{3}}{32 {ω_{0}}^{2}}) c o s 3 ϑ + \frac{3 ε^{2} ζ_{1}^{2} k^{5}}{3072 {ω_{0}}^{4}} c o s 5 ϑ . \end{array}

From Eq. (14) and Eq. (35), the displacement function of nonlinear vibration of rectangular orthotropic film with damping is obtained:

37

w (x, y, t) = \sum_{m = 1}^{\infty} \sum_{n = 1}^{\infty} s i n \frac{m π x}{a} c o s \frac{n π y}{b} k c o s ϑ

+ (\frac{3 ε^{2} ζ_{1}^{2} k^{5}}{512 {ω_{0}}^{4}} - \frac{ε ζ_{1} k^{3}}{32 {ω_{0}}^{2}}) c o s 3 ϑ + \frac{3 ε^{2} ζ_{1}^{2} k^{5}}{3072 {ω_{0}}^{4}} c o s 5 ϑ .

3. Results and discussions

The parameters of the micro film are shown in Table 1 (here, $k_{0} =$ 2×10^-7m, $U_{0} =$ 0.1 $v$ , $σ_{0 y} =$ 0), Table 2 gives the changes of nonlinear frequencies (here, $ε =$ 0.001), $ω_{0}$ is the nonlinear frequencies of the micro film without considering the Casimir force, $ω_{1}$ is the nonlinear frequencies of the micro film with considering the Casimir force, $η$ is the relative deviations between them. Fig. 2 gives the comparisons of the first four orders of the nonlinear frequencies for different nonlinear parameters. Fig. 3 gives nonlinear frequency changes with the main parameters.

Table 1System parameters

$a$ (mm)	$b$ (mm)	$h$ (μm)	$v$ (μm)	$ε_{0}$ ( $c$ ²·N^-1·m^-2)	$E_{1}$ (GPa)	$E_{2}$ (GPa)	$ρ$ (kg/m³)
0.8	0.3	1	0.3	8.85×10^-12	1.4	0.9	2330

From Table 2, Fig. 3 and Fig. 4, the following observations are worth noting:

1) Nonlinear resonant frequencies without considering the Casimir force are larger than those with considering the Casimir force. The Casimir force and electrostatic force correspond to two springs in series, so the Casimir force can lead to a decrease of the nonlinear resonant frequencies just like the electrostatic force.

2) For $ε =$ 0.001, the deviation between the nonlinear frequencies of the micro sensor with and without the Casimir force decreases with increasing the order number of the mode. For the first order frequency, the deviation between the nonlinear frequencies is 19.51 %, for the fourth order one, the deviation between the nonlinear frequencies is 0.796 %. It shows that the Casimir force has a greater influence on the low-order nonlinear frequencies. So, the Casimir force should be considered when determining the low order of the resonant frequencies for the micro film.

3) As the nonlinear parameter increases, the first four order nonlinear frequencies decrease, and the deviation between the nonlinear frequencies with and without considering the Casimir force decreases. The deviation between the nonlinear frequencies with considering the Casimir force is larger than that without considering the Casimir force. It shows that nonlinearity of the Casimir force has an effect on the resonant frequency of the micro film, but the nonlinearity of the electrostatic force has much larger effect on the resonant frequency of the micro film when the nonlinearity is stronger.

4) As the film length increases, the deviation between the nonlinear frequencies for $ε =$ 0 and $ε =$ 0.01 increases significantly. The deviation between the nonlinear frequencies of the micro sensor with considering the Casimir force is larger than those without considering the Casimir force. It is because the effects of the Casimir force become large when the film length is large.

5) As the initial clearance between the micro film and base plate increases, the deviation between the nonlinear frequencies with and without considering the Casimir force decreases. When the initial clearance is above 400 nm, the nonlinear frequencies with and without considering the Casimir force are nearly identical to each other. It shows that the Casimir force should be considered when the initial clearance is below 400 nm. It is because the Casimir force is inversely proportional to the fourth power of the initial clearance.

Table 2Fluctuations of nonlinear frequencies

	Mode (1, 1)	Mode (2, 2)	Mode (3, 3)	Mode (4, 4)
$ω_{0}$ (rad/s)	157596.58	338485.24	513937.67	688124.72
$ω_{1}$ (rad/s)	131863.64	327295.31	506637.69	682689.83
$η$ (%)	19.51	3.419	1.441	0.7961

Fig. 3Frequencies for different nonlinear parameters ε

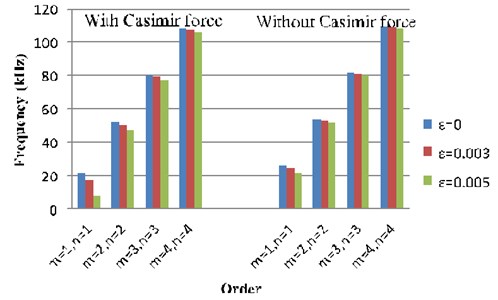
Fig. 4Nonlinear frequency error changes with parameters

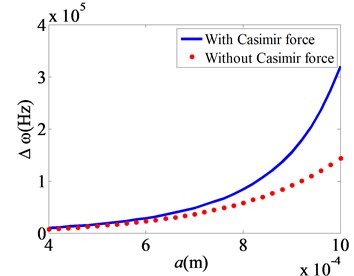
a) $a$ changes

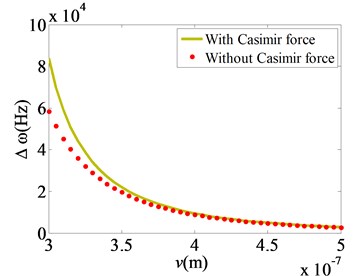
b) $v$ changes

The effects of the Casimir force, small parameter and air damping force on the nonlinear vibrating amplitudes are investigated for the mode (1, 1) (see Fig. 5, Fig. 6 and Fig. 7). Fig. 5 gives the vibrating amplitudes of nonlinear free vibration at $ε =$ 0.01 with considering the Casimir force. Fig. 6 gives the difference of the vibrating amplitudes with and without considering the Casimir force ( $ε =$ 0.01). Fig. 7 gives the vibrating amplitudes of nonlinear free vibration for $ε =$ 0.01 and $ε =$ 0 (considering the Casimir force).

From Fig. 5, Fig. 6 and Fig. 7, the following observations are worth noting:

1) The displacement time trace of free vibration at each point on the micro film reduces periodically with the time. Due to the existence of air damping, the amplitude eventually approaches zero.

2) The vibration amplitude of the center point B is much smaller than that of point A and point C. This is because the distances between the center point B and two free film edges are equal, and this makes part of the vibrations cancel each other after superimposing on the center point B. For point A and point C, the nonlinear vibration direction is opposite. This is due to the fact that two points are symmetrical about the film midpoint, and the motions of two points mainly depend on the first order of the vibrating mode.

Fig. 5Displacement variation of nonlinear free vibration

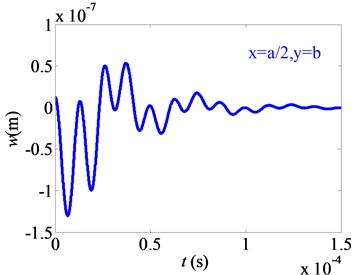
a) Point A ( $x = a / 2$ , $y = b$ )

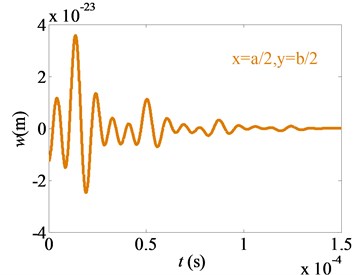
b) Point B ( $x = a / 2$ , $y = b / 2$ )

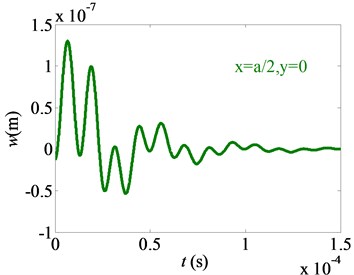
c) Point C ( $x = a / 2$ , $y = 0$ )

Fig. 6Effects of Casimir force on difference of nonlinear free vibration (ε= 0.01)

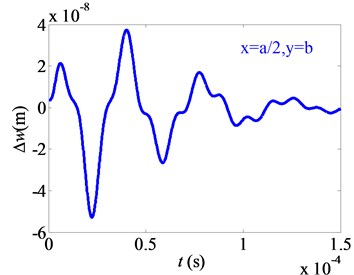
a) Point A ( $x = a / 2$ , $y = b$ )

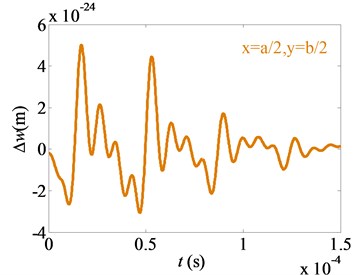
b) Point B ( $x = a / 2$ , $y = b / 2$ )

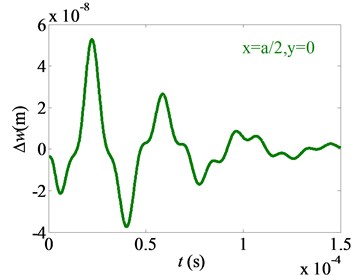
c) Point C ( $x = a / 2$ , $y = 0$ )

Fig. 7Effects of small parameter on difference of nonlinear free vibration

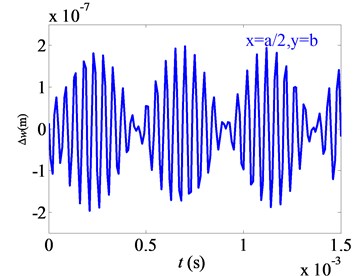
a) Point A ( $x = a / 2$ , $y = b$ )

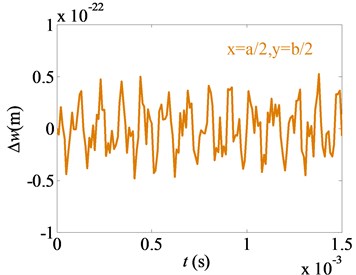
b) Point B ( $x = a / 2$ , $y = b / 2$ )

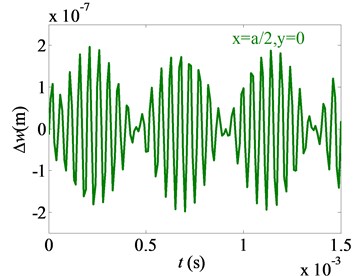
c) Point C ( $x = a / 2$ , $y = 0$ )

3) The difference between the vibrating amplitudes with and without considering the Casimir force reduces periodically as well. It shows that the Casimir force have an important effect on vibration amplitude of the micro film. For the point A and point C, the difference between the vibrating amplitudes with and without considering the Casimir force gets to 50 % of its vibration amplitude. For the point B, the difference between the vibrating amplitudes with and without considering the Casimir force is above 10 % of its vibration amplitude. It shows that the Casimir force should be considered when determining the vibration amplitudes of the micro film.

4) The difference between the vibrating amplitudes for $ε =$ 0.01 and $ε =$ 0 changes periodically for the points A, B point C. The difference does not reduce with the time. It shows that a high order of the harmonic vibrations on the micro film does not decay with the time.

To illustrate the above mentioned analysis about the nonlinear frequencies of the micro film, a micro film resonant sensor is fabricated by lithography, etching and other processes (see Fig. 8(a)). The detection of the natural frequencies for the micro resonant sensor is done. Here, the detecting method of electrostatic excitation and capacitance measurement is used to measure the vibration frequency. When the input signal frequency is close to the resonant frequency of the film, the film resonance occurs. Fig. 8 shows the sensor and its measuring system. Fig. 9 gives detection results of the micro film for two different size sensors (see Table 3). Table 4 gives the comparison between measured results and calculative values ( $η$ is the relative deviation of measured results and calculative values).

Table 3Parameters of measured micro-film

Small size sensor					Large size sensor
$a_{1}$ (mm)	$b_{1}$ (mm)	$v_{1}$ (μm)	$h_{1}$ (μm)	$U_{0}$ ( $v$ )	$a_{2}$ (mm)	$b_{2}$ (mm)	$v_{2}$ (μm)	$h_{2}$ (μm)	$U_{0}$ ( $v$ )
0.96	0.31	0.3	10	0.1	1.50	0.61	1	10	0.1

Table 4Comparison between measured results and calculative values

	Test results	Calculated values
	Test results	With Casimir force ( $ε =$ 0.001)	With Casimir force ( $ε =$ 0)	Without Casimir force ( $ε =$ 0)
Small size sensor
Frequency (kHz)	13.8421	14.3178	15.1149	20.1341
Relative deviation $η$ (%)		3.436	9.195	45.46
Large size sensor
Frequency (kHz)	13.9737	14.6214	14.6258	14.6353
Relative deviation $η$ (%)		4.635	4.667	4.734

Fig. 8Micro film resonant sensor and its measuring system

a) Resonator

b) Sensor

c) Measuring system

Fig. 9Frequency test of micro film for two different size sensors

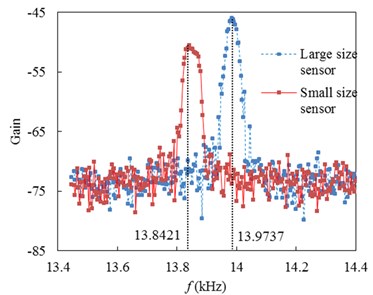
Results show:

1) For a small size sensor, the relative deviation between the measured results and calculative values is 3.436 % (with the Casimir force and $ε =$ 0.001). For a large size sensor, the relative deviation between the measured results and calculative values is 4.635 % (with the Casimir force and $ε =$ 0.001). The measuring frequencies of the micro film are in good agreement with the calculative values.

2) For a small size sensor, the relative deviations between the measured results and calculative values are 3.436 % (with the Casimir force and $ε =$ 0.001), 9.195 % (with the Casimir force and $ε =$ 0) and 45.46 % (without the Casimir force and $ε =$ 0). For a large size sensor, the relative deviations between the measured results and calculative values are 4.635 % (with the Casimir force and $ε =$ 0.001), 4.667 % (with the Casimir force and $ε =$ 0) and 4.734 % (without the Casimir force and $ε =$ 0). Considering the Casimir force and nonlinear parameter, the calculated natural frequency is more near to the test results.

4. Conclusions

In this paper, a multi-field coupled dynamics model of the micro film resonator is proposed. Here, the Casimir force, air damping force, elastic force and electrostatic force are considered. Using a model, the nonlinear vibration frequency and displacement response of the micro film resonator are investigated. Results show:

1) The Casimir force has an important effect on the vibration frequencies of the micro resonant film. When the clearance between the film and baseplate decreases, the effect becomes more significant. When the clearance is below 400 nm, the effect should be considered.

2) When the size of the film increases, the effect of the Casimir force on the nonlinear frequencies of the micro resonant film becomes more significant as well.

3) The Casimir force has a significant important effect on the vibrating amplitudes of the micro film. When determining the vibrating amplitudes of the micro film, the Casimir force should not be neglected.

4) Effects of the Casimir force can be illustrated by detecting the resonant frequency difference of the micro film under different initial clearances.

References

Thielicke E., Obermeier E. Microactuators and their technologies. Mechatronics, Vol. 10, Issues 4-5, 2000, p. 431-455.

Publisher
Rafael N. G., Anna M. B., Alfons D. AC transfer function of electrostatic capacitive sensors based on 1-D equivalent model: application to silicon microphones. Journal of Microelectromechanical Systems, Vol. 12, Issue 6, 2003, p. 972-978.

Publisher
Yuan W., Ren S., Deng J., et al. Review of silicon micromachined resonant pressure sensor. Journal of Mechanical Engineering, Vol. 49, Issue 20, 2013, p. 2-9.

Publisher
Kumar D. D., Kumar N., Kalaiselvam S., et al. Micro-tribo-mechanical properties of nanocrystalline TiN thin films for small scale device applications. Tribology International, Vol. 88, 2015, p. 25-30.

Publisher
Gerhard M., Sebastian B., Sumit P. Novel chemical sensor applications in commercial aircraft. Procedia Engineering, Vol. 25, 2011, p. 16-22.

Publisher
Lizhong Xu, Xiaorui Fu Electromechanical fluidic coupled vibrations for micro film considering van der Waals force. Journal of Vibroengineering, Vol. 17, Issue 1, 2015, p. 455-467.

Search CrossRef
Lin W. Free vibration analysis of plane membranes by finite element method. Journal of Dynamics and Control, 2010.

Search CrossRef
García-Alonso A., García J., Castaño E., et al. Strain sensitivity and temperature influence on sputtered thin films for piezo-resistive sensors. Sensors and Actuators A: Physical, Vols. 37-38, Issue 38, 1993, p. 784-789.

Publisher
Fan S. Investigation on nonlinear vibration characteristics of resonant silicon microstructure pressure sensor. Chinese Journal of Scientific Instrument, Vol. 27, Issue 12, 2006, p. 1670-1673.

Search CrossRef
Capasso F., Munday J. N., Iannuzzi D., et al. Casimir forces and quantum electrodynamical torques: physics and nanomechanics. IEEE Journal of Selected Topics in Quantum Electronics, Vol. 13, Issue 2, 2007, p. 400-414.

Publisher
Reutskiy S. Y. Vibration analysis of arbitrarily shaped membranes. Computer Modeling in Engineering and Sciences, Vol. 51, Issue 2, 2009, p. 115-142.

Search CrossRef
Gonçalves P. B., Soares R. M., Pamplona D. Nonlinear vibrations of radially stretched circular hyperelastic membrane. Journal of Sound and Vibration, Vol. 327, Issues 1-2, 2009, p. 231-248.

Publisher
Changjiang Liu, Zhoulian Zheng, Long Jun, et al. Dynamic analysis for nonlinear vibration of pre-stressed orthotropic membranes with viscous damping. International Journal of Structural Stability and Dynamics, Vol. 13, Issue 2, 2013, p. 60-66.

Search CrossRef
Sorokin V. M., Yashchenko A. K. Vibrations of frameless film membrane stabilized by Ampère force in zero gravity. Journal of Applied Mechanics and Technical Physics, Vol. 54, Issue 54, 2013, p. 885-893.

Publisher
Weber J., Link M., Primig R., et al. Sensor for ambient pressure and material strains using thin film bulk acoustic resonator. Ultrasonics Symposium, 2005, p. 1258-1261.

Search CrossRef
Uhlig S., Rau S., Schultes G. Piezoresistivity of polycrystalline silicon applying AIC process-route. Sensors and Actuators A: Physical, Vol. 172, Issue 2, 2011, p. 447-454.

Publisher
Zhao X., Ashley G. M., Garcia-Gancedo L., et al. Protein functionalized ZnO thin film bulk acoustic resonator as odorant biosensor. Sensors and Actuators B Chemical, Vol. 163, Issue 1, 2012, p. 242.

Publisher
Jiang Y., Kanda K., Iga Y., et al. Monolithic integration of Pb(Zr,Ti)O₃, thin film based resonators using complete dry microfabrication process. Microsystem Technologies, Vol. 19, Issue 1, 2013, p. 137-142.

Publisher
Gualdino A., Chu V., Conde J. P. Study of out-of-plane vibrational modes in thin-film amorphous silicon micromechanical disk resonators. Journal of Applied Physics, Vol. 113, Issue 17, 2013, p. 213506.

Publisher
Ren S., Yuan W., Qiao D., et al. Micromachined pressure sensor with integrated resonator operating at atmospheric pressure. Sensors, Vol. 13, Issue 12, 2013, p. 17006-17024.

Publisher
Hamelin B., Daruwalla A., Ayazi F. Stiffness trimming of high Q MEMS resonators by excimer laser annealing of germanium thin film on silicon. International Conference on MICRO Electro Mechanical Systems, 2016, p. 1026-1029.

Publisher
Alahnomi R. A., Zakaria Z., Ruslan E., et al. High sensitive microwave sensor based on symmetrical split ring resonator for material characterization. Microwave and Optical Technology Letters, Vol. 58, Issue 9, 2016, p. 2106-2110.

Publisher
Pan J., Ming G. U. Geometric nonlinear effect to square tensioned membrane’s free vibration. Journal of Tongji University, 2007.

Search CrossRef
Geyer B., Klimchitskaya G. L., Mostepanenko V. M. Analytic approach to thermal Casimir force between metaland dielectric. Annals of Physics, Vol. 323, 2008, p. 291-316.

Publisher
Liu C. J., Zheng Z. L., He X. T., et al. L-P perturbation solution of nonlinear free vibration of pre-stressed orthotropic membrane with large amplitude. Mathematical Problems in Engineering, Vol. 2010, 2010, p. 242-256.

Publisher
Awrejcewicz J., Krys’ko V. A., Shitikova M. V. Nonclassical thermoelastic problems in nonlinear dynamics of shells: applications of Bubnov-Galerkin and finite difference numerical methods. Applied Mechanics Reviews, Vol. 57, Issue 1, 2012, p. B6-B7.

Publisher
Shin C., Kim W., Chung J. Free in-plane vibration of axially moving membrane. Journal of Sound and Vibration, Vol. 272, Issue 1, 2004, p. 137-154.

Publisher
Liu Yanzhu, Chen Wenliang, Chen Liquan Mechanic of Vibrations. Higher Education Press, Beijing, 1998, p. 201-206.

Search CrossRef

Cited by

Nonlinear primary resonance and bifurcation analyses of a micro-resonant pressure sensor

Xiaorui Fu | Chong Li

(2022)

A Compensation Method for Nonlinear Vibration of Silicon-Micro Resonant Sensor

Yan Li | Hao Li | Yifeng Xiao | Le Cao | Zhan-She Guo

(2021)

Coupled chaotic vibration considering resonator mass change of micro-resonant gas sensor

Xiaorui Fu | Lizhong Xu

(2020)

Multi-field coupled chaotic vibration for a micro resonant pressure sensor

Xiaorui Fu | Lizhong Xu

(2019)

About this article

Received

03 February 2017

Accepted

09 May 2017

Published

31 December 2017

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2017.18226

Keywords

Casimir force

multi-field coupled

nonlinear vibration

orthotropic micro film

Acknowledgements

This Project is supported by the Key Basic Research Foundation in the Hebei Province of China (13961701D) and Graduate Innovation Fund of Hebei Province (CXZZBS2017043).

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this article.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2016 11 15

Nonlinear dynamic analysis of a coupled lateral-torsional spur gear with eccentricity

Zhaohui Ren, Jialin Li, Kai Wang, Shihua Zhou

Research article

2016 05 15

Nonlinear free vibration analysis of nanobeams under magnetic field based on nonlocal elasticity theory

Tai-Ping Chang

Research article

2016 05 15

A new model for stability analysis of electromechanical nano-actuator based on Gurtin-Murdoch and consistent couple-stress theories

Maryam Keivani, Ali Koochi, Mohamadreza Abadyan

Research article

2015 12 30

Nonlinear dynamic analysis for high speed gear-rotor-bearing system of the large scale wind turbine

Shihua Zhou, Guiqiu Song, Mengnan Sun, Zhaohui Ren

X. Fu and L. Xu, “Effects of Casimir force on multi-field coupled nonlinear vibration of orthotropic micro film,” Journal of Vibroengineering, Vol. 19, No. 8, pp. 5702–5718, Dec. 2017, https://doi.org/10.21595/jve.2017.18226

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2017.18226
UR  - https://doi.org/10.21595/jve.2017.18226
TI  - Effects of Casimir force on multi-field coupled nonlinear vibration of orthotropic micro film
T2  - Journal of Vibroengineering
AU  - Xu, Lizhong
AU  - Fu, Xiaorui
PY  - 2017
DA  - 2017/12/31
PB  - JVE International Ltd.
SP  - 5702-5718
IS  - 8
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Xu_2017,
	doi = {10.21595/jve.2017.18226},
	url = {https://doi.org/10.21595/jve.2017.18226},
	year = 2017,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {8},
	pages = {5702--5718},
	author = {Lizhong Xu and Xiaorui Fu},
	title = {Effects of Casimir force on multi-field coupled nonlinear vibration of orthotropic micro film},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]L. Xu and X. Fu, “Effects of Casimir force on multi-field coupled nonlinear vibration of orthotropic micro film,” Journal of Vibroengineering, vol. 19, no. 8, pp. 5702–5718, Dec. 2017, doi: 10.21595/jve.2017.18226.

Copy IEEE

Copied to clipboard!

Xu, Lizhong, and Xiaorui Fu. “Effects of Casimir Force on Multi-Field Coupled Nonlinear Vibration of Orthotropic Micro Film.” Journal of Vibroengineering 19, no. 8 (December 31, 2017): 5702–18. https://doi.org/10.21595/jve.2017.18226.

Copy Chicago

Copied to clipboard!

Effects of Casimir force on multi-field coupled nonlinear vibration of orthotropic micro film

Abstract

1. Introduction

2. Coupled dynamics equations

3. Results and discussions

4. Conclusions

References

Cited by

About this article

Related Articles