A novel high-strength large vibrating screen with duplex statically indeterminate mesh beam structure

Wang, Zhenqian; Liu, Chusheng; Wu, Jida; Jiang, Haishen; Song, Baocheng; Zhao, Yuemin

doi:10.21595/jve.2017.18319

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 December 2017

Check for updates

A novel high-strength large vibrating screen with duplex statically indeterminate mesh beam structure

Zhenqian Wang¹

Chusheng Liu²

Jida Wu³

Haishen Jiang⁴

Baocheng Song⁵

Yuemin Zhao⁶

^{1, 2, 3, 5}School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou, 221116, China

^{4, 6}School of Chemical Engineering and Technology, China University of Mining and Technology, Xuzhou, 221116, China

Corresponding Author:

Chusheng Liu

Cite the article Download PDF

Downloads 2760

WoS Core Citations 14

CrossRef Citations 15

Abstract

Screening is an indispensable unit process for separation of materials. Large vibrating screen is extensively used in coal processing because of its large production capacity. In this study, a novel large vibrating screen with duplex statically indeterminate mesh beam structure (VSDSIMBS) was presented. The dynamic model of VSDSIMBS was proposed, and characteristic parameters were obtained by theoretical calculations. In order to obtain more reliable and believable research results, model of a traditional vibrating screen (TVS) with the same mass was also established for comparisons with VSDSIMBS. The finite element (FE) method was applied to study the performance of VSDSIMBS and FE analysis of VSDSIMBS and TVS was completed by using characteristic parameters. Modal analysis results indicated that VSDSIMBS could avoid the resonance and run more smoothly than TVS. Furthermore, harmonic response analysis results showed that VSDSIMBS could improve the entire stress distribution, reduce high stress areas, and increase the strength of vibrating screen. With DSIMBS, the maximum stress of vibrating screen decreased from 130.53 to 64.54 MPa. The full-scale experimental tests were performed to validate the credibility and accuracy of FE analysis results. The stress and displacements of VSDSIMBS were measured under working conditions. The test results obtained are in good agreement with simulation results, and accord with conclusions made from FE analysis.

1. Introduction

Screening is an indispensable unit process for separation of materials in various industrial processes [1-2]. It is the oldest yet most important unit operation for coal processing. Vibrating screen is the key screening equipment in coal preparation and utilization, and widely used in the classification, dewatering, medium draining, and desliming of coal [3-5]. Attributed to its high capacity, large vibrating screen can simplify the coal preparation process, and reduce the initial cost [6-7]. With the increasing number of large-scale coal mines and coal preparation plants, the demand for large scale vibrating screen is becoming huge and progressively urgent [8-9].

With the increase in the screening area and capacity, the participating mass of a large vibrating screen is becoming huge. Thus, the vibrating screen has to bear the alternating heavy loading at high vibrating frequency [10]. This can lead to fractures of beams and cracking of side plates. Furthermore, a low reliability of screen structure, a low screening efficiency, high energy consumption, and a short product life can result [11]. Consequently, it cannot meet the production requirement of a large coal preparation plant. Therefore, a large-scale vibrating screen with high strength and rigidity is urgently needed.

Till date, extensive research efforts have been devoted to the study of large vibrating screens. Baragetti and Villa presented an innovative design strategy for the optimization of the dynamic performances and the structural loads of heavy loaded vibrating screens [12], and Baragetti proposed a new design solution for heavy loaded vibrating screens which allowed the enhancement of structural resistance and the dynamic performances of a vibrating screen for inert materials [13]. Jiang et al. proposed a novel large vibrating screen driven externally by an unbalanced two-axle excitation with a large span, and experimentally proved the excellent performance for coal screening [14-15]. Zhang et al. predicted the physical characteristics of a large vibrating screen from its scale-down model, and provided an effective method for structural optimization and substructure coupling analysis of the large vibrating screen [16]. Peng et al. improved the design of beam structures in large vibrating screen by considering bending and random vibration [17], and proposed a novel and feasible twice-suspended-mass method to deal with the seldom-studied issue of fault diagnosis for damping springs of large vibrating screen [18]. Cleary et al. used the discrete element method (DEM) to simulate a full industrial scale double deck banana screen for a range of accelerations [19-20]. Fernandez et al. introduced the use of smoothed particle hydrodynamics (SPH) to model the flow of slurry (water and fine material) through a double deck banana screen [21]. Zhou calculated and analyzed natural modes and distribution of dynamic stress of lateral plates [22]. Du et al. established five-freedom dynamic model and stability equations of the variable linear vibration screen based on power balance method [23]. Zhang and Wang built the dynamic model of polyurethane screen deck in sieving [24], and Zhang and Xu used the critical plane method for calculating the fatigue lives of the large linear vibrating screen [25].

However, most of these large vibrating screens always suffer from the strong external harmonic exciting force and the impact from the minerals, which easily lead to the fracture of the beam and the crack of the side plate. This has a negative effect on the reliability of the equipment itself and the industrial production. Therefore, considering the essential high reliability of the equipment, a novel large vibrating screen with duplex statically indeterminate mesh beam structure (VSDSIMBS) was put forward and patented [26]. This structure breaks through the limitation of traditional theory. The theory of statically indeterminate structure was applied to design large vibrating screen, and the DSIMBS was invented. This work is the intensive study on the basis of original work by Zhao et al. [10, 27]. In this study, the structure of DSIMBS was redesigned to improve the bearing capacity and the structural strength. Theoretical analysis, FE analysis, and experimental validation were conducted to research the dynamic characteristics and structural strength of VSDSIMBS. Moreover, in order to obtain more reliable and believable research results, model of a traditional vibrating screen (TVS) with the same mass was also established for comparisons with VSDSIMBS.

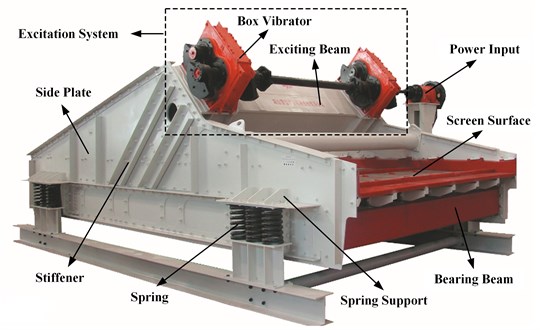
2. Comparison of structure between VSDSIMBS and TVS

TVS is made up of screen body, screen surface, springs, and excitation system as shown in Fig. 1(a). The screen body includes side plates, bearing beams, spring supports, and stiffeners. The excitation system consists of two box vibrators connected with universal couplings. Box vibrators are fixed on exciting beam with high-strength bolts. With the rotation of the eccentric blocks within box vibrators, the screen body vibrates. Therefore, the connections between exciting beam and box vibrators bear alternating force. It has a high requirement on bearing alternating force and resisting deformation for connections.

Fig. 1(b) exhibits the structure of VSDSIMBS. Major components consist of screen body, screen surface, springs, and excitation system. The excitation system of VSDSIMBS is the DSIMBS, made up of four statically indeterminate plates, 16 mesh beams, and eight eccentric blocks as shown in Fig. 2. The length of beam significantly influences the deformation. Deformation increases with the increase in the length of the beam. Thus, the long beam was separated into multiple sections under permitting conditions, to considerably reduce the length of beam. By replacing box vibrators with eccentric blocks, the excitation system leads to the uniform distribution of the exciting force on DSIMBS, and reduces the deformation.

Fig. 1Structures of TVS and VSDSIMBS

a)

b)

Fig. 2Structure of DSIMBS

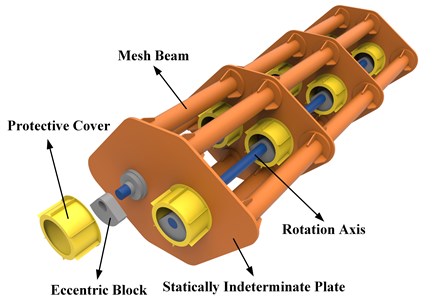
Multiple tubular beams with small diameter constitute the main load-bearing structure. Between these beams, statically indeterminate plates are applied to support each other. The beams and plates constitute DSIMBS. Redundant constraints in the interior of DSIMBS can change the stress distribution, decrease the peak stress, reduce the structural deformation, and improve the strength and rigidity of vibrating screen.

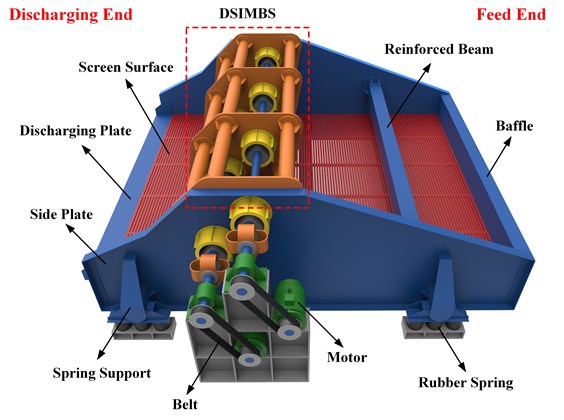
VSDSIMBS has been successfully applied and promoted in industrial field. C2WS4050, the prototype of VSDSIMBS, has been applied at Baodian coal preparation plant, Yankuang Group, Shandong, China in 2014. This vibrating screen is used to dewater and drain medium for coal gangue in heavy medium separation. The medium is recycled, and the water content of gangue decreases, and the corresponding process is shown in Fig. 3. C2WS4050 would be the object to research characteristics of VSDSIMBS in this study, and its structure is shown in Fig. 4.

Fig. 3Process chart of coal preparation plant

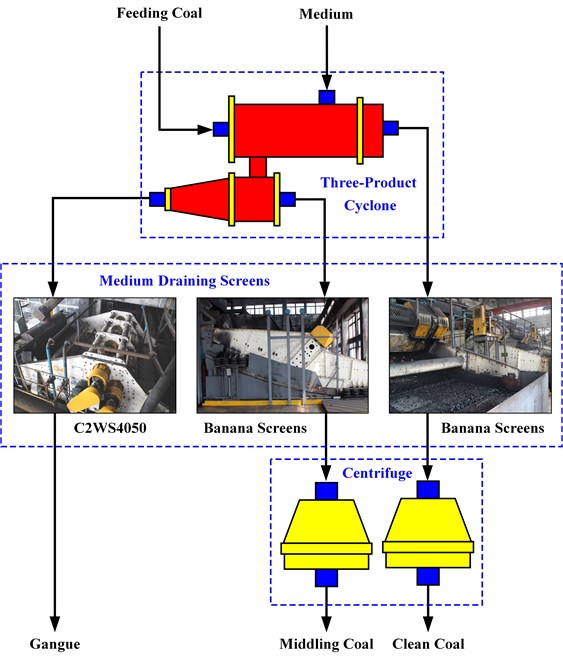
Fig. 4Structure of C2WS4050

3. Dynamic model calculation of VSDSIMBS

Prior to the FE analysis, the dynamic theoretical calculation was necessary to obtain relevant setting parameters, such as stiffness coefficient and exciting force. The natural frequency and displacement amplitude in horizontal and vertical directions of the vibrating screen could also be obtained by dynamic theory analysis. These parameters reflect the natural characteristics of the vibrating screen, and provide an important standard to evaluate the design rationality of the vibrating screen. VSDSIMBS is a type of dual-motors driving linear screen. The direction of the exciting force passes through the centroid of screen body. Ignoring the error caused by manufacturing, two degrees of freedom (2-DOF) dynamic model of C2WS4050 was built as shown in Fig. 5.

Fig. 5Dynamic model of VSDSIMBS

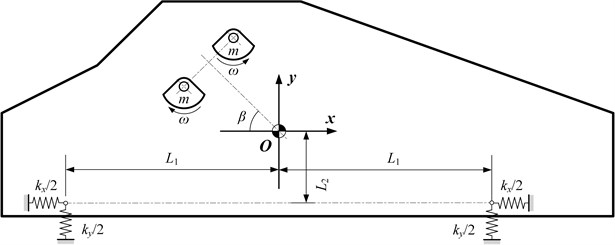
3.1. Calculation of stiffness

12 rubber springs are used in C2WS4050. Compared to metal spring, rubber spring causes less noise, smaller amplitude when passing through resonance region, and it is beneficial to design by changing shape and stiffness according to requirements. The shore hardness ( $H S$ ) of rubber spring in use was measured by shore durometer. Shear modulus ( $G$ ) and tension and compression modulus ( $E$ ) can be obtained by using Eqs. (1-3):

1

G = 0.117 e^{0.03 H S},

2

E = i G,

3

i = 3.6 [1 + 1.65 {(\frac{D - d}{4 h})}^{2}] .

Shear stiffness ( $k_{s}$ ) and tension and compression stiffness ( $k_{t}$ ) of a single rubber spring can be calculated through Eq. (4). Total stiffness of all rubber springs in horizontal and vertical directions ( $k_{x}$ , $k_{y}$ ) can be obtained by using Eq. (5):

4

\{\begin{array}{l} k_{s} = G \frac{π (D^{2} - d^{2})}{4 h}, \\ k_{t} = E \frac{π (D^{2} - d^{2})}{4 h}, \end{array}

5

\{\begin{array}{l} k_{x} = 12 k_{s}, \\ k_{y} = 12 k_{t} . \end{array}

3.2. Calculation of characteristic parameters

The rotational speed of eccentric block ( $n$ ) was measured during field test and the angular velocity of eccentric block ( $ω$ ) can be obtained through Eq. (6):

6

ω = \frac{2 π n}{60} .

When the eccentric blocks are rotating, the exciting force ( $F$ ) is directional harmonic force. The value of exciting force can be calculated by using Eq. (7). The exciting force in horizontal and vertical directions ( $F_{x}$ , $F_{y}$ ) can be obtained through Eq. (8):

7

F = 2 m e ω^{2} s i n ω t,

8

\{\begin{array}{l} F_{x} = 2 m e ω^{2} s i n ω t c o s β, \\ F_{y} = 2 m e ω^{2} s i n ω t s i n β . \end{array}

The differential equation of the vibration system is established as follows:

9

\{\begin{array}{l} M \ddot{x} + c_{x} \dot{x} + k_{x} x = 2 m e ω^{2} s i n ω t c o s β, \\ M \ddot{y} + c_{y} \dot{y} + k_{y} y = 2 m e ω^{2} s i n ω t s i n β . \end{array}

Assuming that the displacement in horizontal and vertical directions ( $x$ , $y$ ) has the following forms:

10

\{\begin{array}{l} x = A_{x} s i n (ω t - α_{x}), \\ y = A_{y} s i n (ω t - α_{y}) . \end{array}

Thus, the velocity and acceleration can be calculated through Eq. (11):

11

\{\begin{array}{l} \dot{x} = A_{x} ω c o s (ω t - α_{x}), \\ \ddot{x} = - A_{x} ω^{2} s i n (ω t - α_{x}), \\ \dot{y} = A_{y} ω c o s (ω t - α_{y}), \\ \ddot{y} = - A_{y} ω^{2} s i n (ω t - α_{y}) . \end{array}

Substituting Eqs. (10-11) into Eq. (9), the displacement amplitude ( $A_{x}$ , $A_{y}$ ) and phase angle ( $α_{x}$ , $α_{y}$ ) can be obtained as follows:

12

\{\begin{array}{l} A_{x} = \frac{2 m e ω^{2} c o s β}{\sqrt{(k_{x} - M ω^{2})^{2} + (c_{x} ω)^{2}}}, \\ A_{y} = \frac{2 m e ω^{2} s i n β}{\sqrt{(k_{y} - M ω^{2})^{2} + (c_{y} ω)^{2}}}, \\ α_{x} = a r c t a n \frac{c_{x} ω}{k_{x} - M ω^{2}}, \\ α_{y} = a r c t a n \frac{c_{y} ω}{k_{y} - M ω^{2}} . \end{array}

The stiffness in horizontal direction is not equal to that in vertical direction; therefore, the vibration direction of the vibrating screen is different from that of the exciting force. The displacement amplitude in vibrating direction ( $A$ ) and the vibrating direction angle ( $β_{0}$ ) can be obtained through Eqs. (13-14):

13

A = \sqrt{A_{x}^{2} + A_{y}^{2}} = 2 m e ω^{2} \sqrt{\frac{c o s^{2} β}{(k_{x} - M ω^{2})^{2} + (c_{x} ω)^{2}} + \frac{s i n^{2} β}{(k_{y} - M ω^{2})^{2} + (c_{y} ω)^{2}}},

14

t a n β_{0} = \frac{A_{y}}{A_{x}} = \sqrt{\frac{[k_{x} - M ω^{2}]^{2} + (c_{x} ω)^{2}}{[k_{y} - M ω^{2}]^{2} + (c_{y} ω)^{2}}} t a n β .

The damping coefficient of rubber spring has little influence on the vibration system, thus it can be ignored in order to simplify the calculations. Eqs. (12-14) can be simplified to Eqs. (15-17), respectively:

15

\{\begin{array}{l} A_{x} = \frac{2 m e ω^{2} c o s β}{|k_{x} - M ω^{2}|}, \\ A_{y} = \frac{2 m e ω^{2} s i n β}{|k_{y} - M ω^{2}|}, \end{array}

16

A = 2 m e ω^{2} \sqrt{\frac{c o s^{2} β}{(k_{x} - M ω^{2})^{2}} + \frac{s i n^{2} β}{(k_{y} - M ω^{2})^{2}}},

17

t a n β_{0} = \frac{A_{y}}{A_{x}} = \frac{|k_{x} - M ω^{2}|}{|k_{y} - M ω^{2}|} t a n β .

In Eq. (15), when denominator is 0, the first two natural frequencies of the vibration system can be calculated through Eq. (18):

18

\{\begin{array}{l} f_{x} = 2 π \sqrt{\frac{k_{x}}{M},} \\ f_{y} = 2 π \sqrt{\frac{k_{y}}{M} .} \end{array}

Through the calculation of the dynamic model, the dynamic characteristic parameters of VSDSIMBS can be obtained. All parameters used, and calculation results are listed in Table 1.

4. Comparison between VSDSIMBS and TVS by FE method

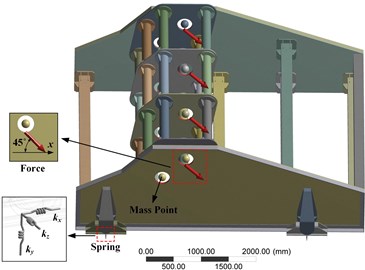
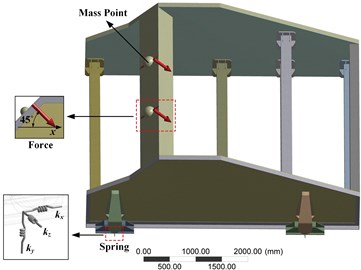
Further, in order to research the performance of VSDSIMBS more accurately, the FE method was applied to dynamic analysis on VSDSIMBS. A TVS with exciting beam was compared to VSDSIMBS with the objective of obtaining more intuitive and reliable analysis results.

An exciting beam was designed with the same mass as DSIMBS by using the traditional design method. Other components of vibrating screen, the value of exciting force and spring stiffness remained the same as VSDSIMBS. Box vibrator was selected to ensure that the exciting force remained unchanged. For the simplicity and accuracy, parts with little effect on strength were ignored, and mass points in FE software were used to replace vibrators and eccentric blocks. The FE models were built by using FE software as shown in Fig. 6. The setting of exciting force and rubber spring was shown in this figure. The model of VSDSIMBS had 1071965 nodes and 222958 elements, and that of TVB had 811861 nodes and 159212 elements. Modal analysis and harmonic response analysis were performed to evaluate and compare the performance of the two types of vibrating screens as presented in Fig. 7.

4.1. Modal analysis of VSDSIMBS and TVS

The natural frequencies and mode shapes can be obtained through modal analysis. By comparing natural frequency with working frequency, it can be conjectured whether resonance occurs in working state. By observing mode shape, the deformation of screen body on natural frequency would be forecasted. Therefore, by utilizing FE software, the first 12 natural frequencies and mode shapes of VSDSIMBS and TVS were obtained, and the corresponding results are listed in Table 2.

Table 1Parameters and calculation results

Parameter	Value
Shear modulus of rubber spring, $G$ (MPa)	0.61
Tension and compression modulus of rubber spring, $E$ (MPa)	2.31
Shore hardness of rubber spring, $H S$	55
Shape coefficient of ring rubber spring, $i$	3.79
Outer diameter of rubber spring, $D$ (mm)	180
Inner diameter of rubber spring, $d$ (mm)	50
Height of rubber spring, $h$ (mm)	180
Shear stiffness of rubber spring, $k_{s}$ (N/mm)	79.48
Tension and compression stiffness of rubber spring, $k_{t}$ (N/mm)	301.52
Total stiffness in horizontal direction, $k_{x}$ (N/mm)	953.77
Total stiffness in vertical direction, $k_{y}$ (N/mm)	3618.25
Total mass of screen body, $M$ (kg)	9105.30
Mass of eccentric block in single axis, $m$ (kg)	296.72
Rotational speed of eccentric block, $n$ (r/min)	831
Angular velocity of eccentric block, $ω$ (rad/s)	87.02
Eccentricity of eccentric block, $e$ (mm)	7.83
Exciting force, $F$ (N)	351882.66
Exciting force in horizontal direction, $F_{x}$ (N)	248818.61
Exciting force in vertical direction, $F_{y}$ (N)	248818.61
Angle between exciting force and horizontal plane, $β$ (°)	45
Horizontal distance between spring support and centroid, $L_{1}$ (mm)	1825
Vertical distance between spring support and centroid, $L_{2}$ (mm)	627.59
Damping coefficient in horizontal direction, $c_{x}$ (Ns/mm)	0
Damping coefficient in vertical direction, $c_{y}$ (Ns/mm)	0
Phase angle in in horizontal direction, $α_{x}$ (°)	0
Phase angle in in vertical direction, $α_{y}$ (°)	0
Displacement amplitude in horizontal direction, $A_{x}$ (mm)	3.66
Displacement amplitude in vertical direction, $A_{y}$ (mm)	3.81
Natural frequency in horizontal direction, $f_{x}$ (Hz)	1.63
Natural frequency in vertical direction, $f_{y}$ (Hz)	3.17
Displacement amplitude in vibrating direction, $A$ (mm)	5.28
Vibrating direction angle, $β_{0}$ (°)	46.14

Fig. 6FE models of: a) VSDSIMBS, b) TVS

a)

b)

Fig. 7Flow chart of FE analysis

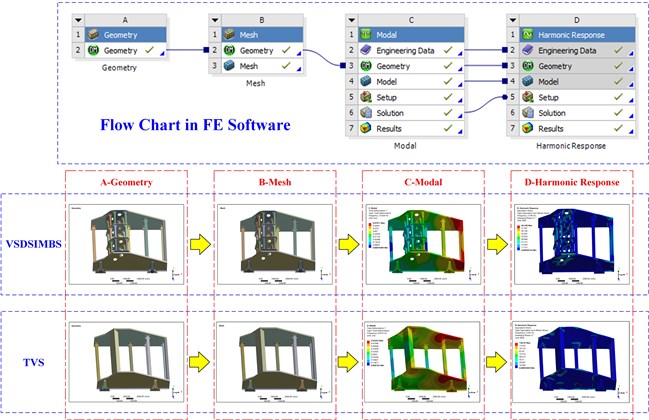
Table 2Natural frequencies and mode shapes of VSDSIMBS and TVS

Order	VSDSIMBS		TVS
Order	Natural frequency (Hz)	Mode shape	Natural frequency (Hz)	Mode shape
1	1.76	Translation along $x$ axis	1.74	Translation along $z$ axis
2	1.77	Translation along $z$ axis	1.76	Translation along $x$ axis
3	2.52	Rotation along $y$ axis	2.57	Rotation along $y$ axis
4	3.15	Translation along $y$ axis	3.14	Translation along $y$ axis
5	3.97	Rotation along $z$ axis	3.80	Rotation along $z$ axis
6	4.41	Rotation along $x$ axis	4.74	Rotation along $x$ axis
7	10.92	Reverse translation of discharging plate and baffle along $z$ axis	8.27	Reverse translation of discharging plate and baffle along $z$ axis
8	16.33	Reverse rotation of side plate on both sides along $z$ axis	14.11	Translation of discharging plate along $z$ axis
9	20.62	Translation of discharging plate along $z$ axis	19.76	Reverse translation of discharging plate, DSIMBS, and baffle along $z$ axis
10	24.28	Reverse translation of discharging plate, DSIMBS, and baffle along $z$ axis	20.35	Reverse rotation of side plate on both sides along $z$ axis
11	32.44	Reverse translation of side plate on both sides along $z$ axis	26.18	Reverse translation of reinforced beam and bearing beam along $z$ axis
12	35.86	Reverse translation of DSIMBS and baffle along $z$ axis	32.04	Reverse translation of side plate on both sides along $z$ axis

The values listed in Table 2 indicate that the mode shapes of vibrating screens are mainly rigid motion and bending deformation of screen body. The first six natural frequencies correspond to the rigid motion of vibrating screens. Only the rubber springs were deformed. The values of natural frequencies were just depended on the mass of screen body and stiffness of spring. Therefore, the first six natural frequencies of VSDSIMBS were same as those of TVS. The last 6 natural frequencies were ascribed to the bending deformation of screen body. Clearly, the natural frequencies of VSDSIMBS are much larger and significantly different from the working frequency (13.85 Hz) than those of TVS. These results indicate that VSDSIMBS can avoid the resonance during working, reduce the stress of screen body, and improve the working life effectively.

4.2. Harmonic response analysis of VSDSIMBS and TVS

During the working process, the screen body of vibrating screen bears the alternating force produced by motors. This force would lead to large stress and deformation of key components, such as exciting beam and side plates, of the vibrating screen.

Steady-state response under harmonic load can be obtained by harmonic response analysis. The exciting force is harmonic force, thus the stress and displacement of vibrating screen at working frequency can be obtained by harmonic response analysis.

Fig. 8Stress nephograms of: a) VSDSIMBS, b) TVS

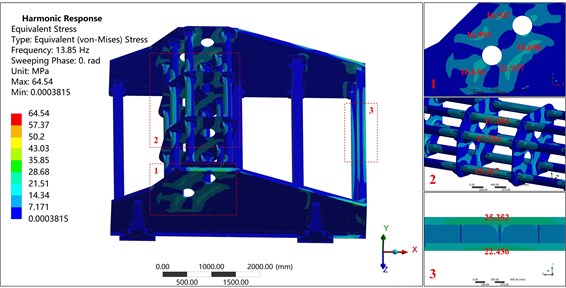
a)

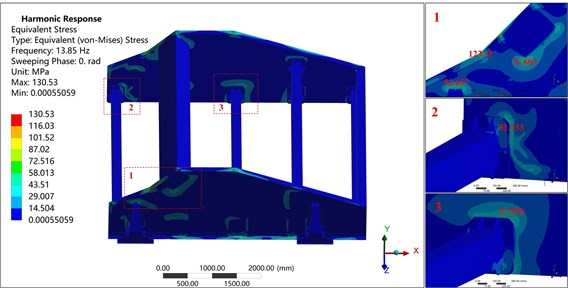
b)

Fig. 8 shows the stress nephograms of VSDSIMBS and TVS at the working frequency (13.85 Hz). Fig. 8(a) clearly demonstrates that the high stress areas of VSDSIMBS are mainly distributed in DSIMBS; the stress in the middle of DSIMBS is larger than that on both sides; and the maximum stress is 64.54 MPa, which is far less than the yield strength of material used (235 MPa). Fig. 8(b) exhibits that the high stress areas of TVS are mainly distributed in side plates, in particular, in the junctions of side plates and beams; and the maximum stress is 130.53 MPa, significantly larger compared to that of DSIMBS.

In order to obtain more direct and obvious computed results, the display of stress nephograms was rebuilt by changing legends as shown in Fig. 9. Fig. 9(a) shows that the stress of VSDSIMBS is generally less than 20 MPa. However, Fig. 9(b) exhibits many areas in side plates of TVS, where stress is larger than 20 MPa, even 30 MPa. Therefore, this result indicates that the overall structural strength of VSDSIMBS is better than that of TVS.

Fig. 9Rebuilt stress nephograms of: a) VSDSIMBS, b) TVS

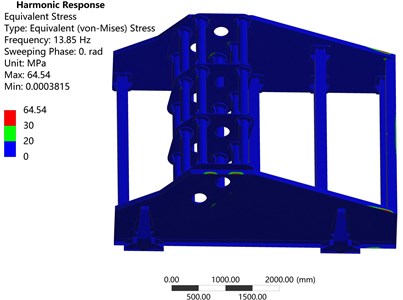
a)

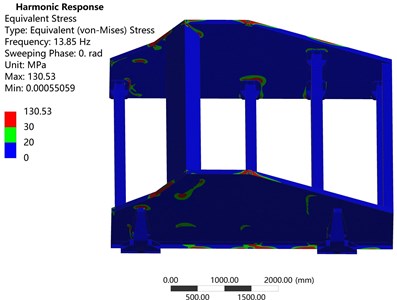
b)

Fig. 10Displacement nephograms of: a) VSDSIMBS, b) TVS

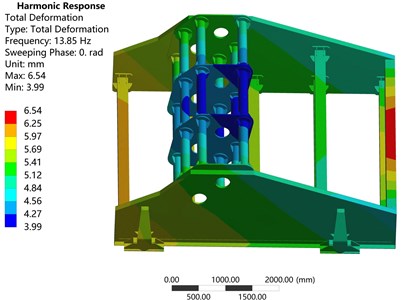
a)

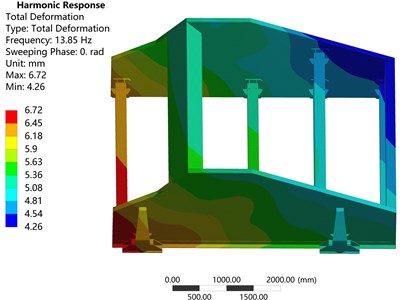
b)

Fig. 10 shows the displacement nephograms of VSDSIMBS and TVS at the working frequency (13.85 Hz). Fig. 10(a) exhibits the displacement nephogram of VSDSIMBS, demonstrating that the displacement of DSIMBS is less than those of feed end and discharging end; and the displacement of feed end is slightly larger than that of discharging end. Fig. 10(b) shows the displacement nephogram of TVS, revealing that the displacement of feed end is far less than that of discharging end. This indicates that TVS swings back and forth with high magnitude under working state. Thus, VSDSIMBS runs more smoothly than TVS.

The simulation results of FE analysis indicate that DSIMBS exhibits greater contacting areas with side plates than traditional exciting beam. This can effectively improve the entire stress and displacement distribution of vibrating screen, and make DSIMBS the main supporting part. Unlike VSDSIMBS, side plates of TVS mainly bear the loading. Compared to side plates, the DSIMBS is easier to be maintained and replaced. Moreover, DSIMBS can reduce the stress of vibrating screen under the same loading conditions, and increase the strength of vibrating screen. Thus, VSDSIMBS has many advantages over TVS.

5. Full-scale experimental tests on VSDSIMBS and comparisons between simulation results and test results

The simulation results indicated that the stress in the middle of DSIMBS was greater than that on both sides, and the displacement of DSIMBS was less than those of feed end and discharging end. In order to verify the credibility and accuracy of simulation results, the field test on VSDSIMBS was necessary. C2WS4050 at coal preparation plant was used as the test object. The stress of DSIMBS was obtained by resistance strain gauges, and 3-axis acceleration sensors were applied to measure the displacements of VSDSIMBS. Related experimental instruments were connected, and test signals were collected and processed [28-31]. The flow chart of field tests is shown in Fig. 11.

Fig. 11Flow chart of field tests

18 resistance strain gauges were, respectively, arranged at 18 mesh beams of DSIMBS to obtain the stress of DSIMBS. Three 3-axis acceleration sensors (A1-A3) were placed at the middle of baffle (A1), DSIMBS (A2), and discharging plate (A3), to measure the displacement of feed end, DSIMBS, and discharging end, separately. The arrangement of gauges and sensors is shown in Fig. 12. Then the stress and displacements were obtained.

Fig. 12Schematic illustration of gauges and sensors arrangement

Simulation results of same measuring points were obtained from FE analysis, and compared with test results listed in Tables 3-4 and shown in Fig. 13.

Table 3 and Fig. 13(a) show that the displacement of DSIMBS (A2) is less than that of feed end (A1) and discharging end (A3). Further, Table 4 and Fig. 13(b) exhibit that the stress in the middle of DSIMBS (B7-B12) is larger than that on both sides (B1-B6, B13-B18).

Table 3Comparison of displacement between test results and simulation results

Measuring point	Test result (mm)	Simulation result (mm)	Relative error
A1	6.39	6.51	1.88 %
A2	3.87	3.99	3.10 %
A3	6.05	6.17	1.98 %

Table 4Comparison of stress between test results and simulation results

Measuring point	Test result (MPa)	Simulation result (MPa)	Relative error
B1	2.00	2.08	3.85 %
B2	2.90	2.81	3.20 %
B3	4.80	4.67	2.84 %
B4	2.50	2.59	3.47 %
B5	5.10	4.85	5.15 %
B6	3.40	3.25	4.62 %
B7	14.20	15.23	6.76 %
B8	16.30	17.48	6.75 %
B9	18.80	17.69	6.27 %
B10	15.90	16.63	4.39 %
B11	16.80	17.24	2.55 %
B12	14.90	15.95	6.58 %
B13	4.50	4.26	5.63 %
B14	4.80	5.08	5.51 %
B15	5.80	6.04	3.97 %
B16	5.20	4.87	6.78 %
B17	5.10	5.34	4.49 %
B18	3.60	3.42	5.26 %

Fig. 13Comparisons of: a) displacement, b) stress between test results and simulation results

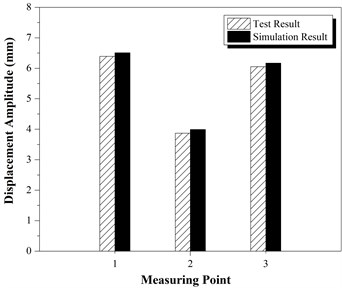
a)

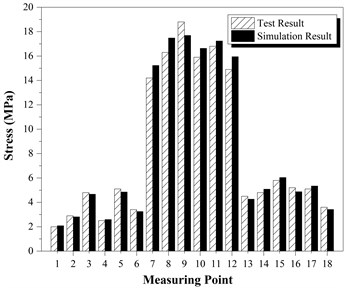
b)

Considering the instrumental precision and field interference, the test results are within acceptable limits. The maximum relative error between simulation result and test result is 6.78 %. According to [13], the errors those are less than 7 % can be considered as negligible. Ignoring tolerance errors, test results are in good agreement with simulation results, and can meet conclusions of FE analysis. This indicates that simulation results have high reliability and accuracy, and conclusions obtained by FE method are in well agreement with the actual working situation.

6. Conclusions

A novel large vibrating screen with DSIMBS was proposed in this study. The dynamic model of VSDSIMBS was set up, and characteristic parameters were obtained by theoretical calculation. The FE analysis of VSDSIMBS and TVS was completed, and the full-scale experimental tests were also accomplished.

1) The natural frequencies of VSDSIMBS were much larger and significantly different from the working frequency than those of TVS. This indicated that VSDSIMBS could avoid the resonance and run more smoothly than TVS during working.

2) The stress of VSDSIMBS was generally less than 20 MPa, while that of parts of TVS was larger than 20 MPa, even 30 MPa. In vibrating screen with DSIMBS, the maximum stress reduced from 130.53 to 64.54 MPa, and the high stress areas decreased under the same conditions. The simulation results showed that VSDSIMBS could improve the entire stress distribution, and increase the strength of vibrating screen.

3) The stress and displacements of VSDSIMBS were measured on the field. The maximum relative error between simulation result and test result was 6.78 %, the test results were in good agreement with simulation results. This indicated that the conclusions obtained by FE method were in well agreement with the actual working situation.

4) This study proved that the DSIMBS had a great influence on performance of vibrating screen. DSIMBS would be conducive to increase the strength and improve the stress distribution of vibrating screen. VSDSIMBS provided a feasible and reliable scheme for large vibrating screen.

References

Dong K. J., Yu A. B., Brake I. DEM simulation of particle flow on a multi-deck banana screen. Minerals Engineering, Vol. 22, Issue 11, 2009, p. 910-920.

Publisher
Jahani M., Farzanegan A., Noaparast M. Investigation of screening performance of banana screens using LIGGGHTS DEM solver. Powder Technology, Vol. 283, 2015, p. 32-47.

Publisher
Makinde O. A., Mpofu K., Popoola A. P. I. Review of the status of reconfigurable manufacturing systems (RMS) application in South Africa mining machinery industries. Proceedings of the 47th Cirp Conference on Manufacturing Systems: Variety Management in Manufacturing, Vol. 17, 2014, p. 136-141.

Publisher
Song B. C., Liu C. S., Peng L. P., Li J. Dynamic analysis of new type elastic screen surface with multi degree of freedom and experimental validation. Journal of Central South University, Vol. 22, Issue 4, 2015, p. 1334-1341.

Publisher
Noble A., Luttrell G. H. A review of state-of-the-art processing operations in coal preparation. International Journal of Mining Science and Technology, Vol. 25, Issue 4, 2015, p. 511-521.

Publisher
Liu K. S. Some factors affecting sieving performance and efficiency. Powder Technology, Vol. 193, Issue 2, 2009, p. 208-213.

Publisher
Zhao L. L., Zhao Y. M., Sao C. Y., Hou Q. F., Yu A. B. Laboratory-scale validation of a DEM model of screening processes with circular vibration. Powder Technology, Vol. 303, 2016, p. 269-277.

Publisher
Wen B. Recent development of vibration utilization engineering. Frontiers of Mechanical Engineering in China, Vol. 3, Issue 1, 2008, p. 1-9.

Publisher
Zhao Y., Liu J., Wei X., Luo Z., Chen Q., Song S. New progress in the processing and efficient utilization of coal. Mining Science and Technology, Vol. 21, Issue 4, 2011, p. 547-552.

Publisher
Zhao Y. M., Liu C. S., He X. M., Zhang C. Y., Wang Y. B., Ren Z. T. Dynamic design theory and application of large vibrating screen. Procedia Earth and Planetary Science, Vol. 1, Issue 1, 2009, p. 776-784.

Publisher
Steyn J. Fatigue failure of deck support beams on a vibrating screen. International Journal of Pressure Vessels and Piping, Vol. 21, Issue 4, 1995, p. 315-327.

Publisher
Baragetti S., Villa F. A dynamic optimization theoretical method for heavy loaded vibrating screens. Nonlinear Dynamics, Vol. 78, Issue 1, 2014, p. 609-627.

Publisher
Baragetti S. Innovative structural solution for heavy loaded vibrating screens. Minerals Engineering, Vol. 84, 2015, p. 15-26.

Publisher
Jiang H. S., Zhao Y. M., Duan C. L., Yang X. L., Liu C. S., Wu J. D., Qiao J. P., Diao H. R. Kinematics of variable-amplitude screen and analysis of particle behavior during the process of coal screening. Powder Technology, Vol. 306, 2017, p. 88-95.

Publisher
Jiang H. S., Zhao Y. M., Duan C. L., Zhang C. Y., Diao H. R., Wang Z. Q., Fan X. C. Properties of technological factors on screening performance of coal in an equal-thickness screen with variable amplitude. Fuel, Vol. 188, 2017, p. 511-521.

Publisher
Zhang Z. R., Wang Y. Y., Fan Z. M. Similarity analysis between scale model and prototype of large vibrating screen. Shock and Vibration, Vol. 2015, 2015, p. 1-7.

Publisher
Peng L. P., Liu C. S., Song B. C., Wu J. D., Wang S. Improvement for design of beam structures in large vibrating screen considering bending and random vibration. Journal of Central South University, Vol. 22, Issue 9, 2015, p. 3380-3388.

Publisher
Peng L. P., Liu C. S., Li J., Wang H. Static-deformation based fault diagnosis for damping spring of large vibrating screen. Journal of Central South University, Vol. 21, Issue 4, 2014, p. 1313-1321.

Publisher
Cleary P. W., Sinnott M. D., Morrison R. D. Separation performance of double deck banana screens – Part 1: Flow and separation for different accelerations. Minerals Engineering, Vol. 22, Issue 14, 2009, p. 1218-1229.

Publisher
Cleary P. W., Sinnott M. D., Morrison R. D. Separation performance of double deck banana screens – Part 2: Quantitative predictions. Minerals Engineering, Vol. 22, Issue 14, 2009, p. 1230-1244.

Publisher
Fernandez J. W., Cleary P. W., Sinnott M. D., Morrison R. D. Using SPH one-way coupled to DEM to model wet industrial banana screens. Minerals Engineering, Vol. 24, Issue 8, 2011, p. 741-753.

Publisher
Zhou N. Dynamic characteristics analysis and optimization for lateral plates of the vibration screen. Journal of Vibroengineering, Vol. 17, Issue 4, 2015, p. 1593-1604.

Search CrossRef
Du C. L., Gao K. D., Li J. P., Jiang H. Dynamics behavior research on variable linear vibration screen with flexible screen face. Advances in Mechanical Engineering, Vol. 2014, 2014, p. 1-12.

Publisher
Zhang Z. R., Wang Y. Y. Deformation analysis of polyurethane screen deck in linear vibrating screen. Advanced Polymer Science and Engineering, Vol. 221, 2011, p. 240-246.

Publisher
Zhang Z. R., Xu J. Fatigue analysis of linear vibrating screen with different surface roughness. Advanced Polymer Processing III, Vol. 561, 2013, p. 564-567.

Publisher
Zhao Y. M., Zhang C. Y. Extra-Large Vibrating Screen with Duplex Statically Indeterminate Mesh Beam. United States Patent, US8074805 B2, 2007.

Search CrossRef
Zhao Y. M., Liu C. S., Li F. M., Peng L. P., Song B. C., Dong H. L., Duan C. L. Dynamic analysis and optimization of a large-scale vibrating screen with high reliability. 27th International Mineral Processing Congress, 2014, p. 116-124.

Search CrossRef
Du J., Xiao P., Wu J., Chen Q. Design of isotropic orthogonal transform algorithm-based multicarrier systems with blind channel estimation. IET Communications, Vol. 6, Issue 16, 2012, p. 2695-2704.

Publisher
Yang K., Yang N., Xing C. W., Wu J. S., Zhang Z. S. Space-time network coding with transmit antenna selection and maximal-ratio combining. IEEE Transactions on Wireless Communications, Vol. 14, Issue 4, 2015, p. 2106-2117.

Publisher
Han F. X., Zhao S. J., Zhang L., Wu J. S. Survey of strategies for switching off base stations in heterogeneous networks for greener 5G systems. IEEE Access, Vol. 4, 2016, p. 4959-4973.

Publisher
Serrano P., Costa Perez X., Wu J., Christensen K. Special issue: green communications. Computer Networks, Vol. 78, 2015, p. 1-3.

Publisher

Cited by

Numerical investigation on dynamic response of the screen mesh in vibrating screening through DEM-FEM co-simulation

Huan Zhang | Xiao Zheng | Weimin Jing

(2024)

Dynamic analysis of beam structure of linear vibrating screen

Hui Long | Chang-Zheng Huang | Dong-Chang Li

(2024)

Finite element analysis and optimization design of large vibrating screen based on equivalent static load method

Xingdong Sun | Yuhang Sui | Yukai Zheng | Li Wang | Haowei Zhu

(2024)

Dynamic characteristics analysis of a circular vibrating screen

Yuanchen Wang | Zhenqian Wang | Min Zhang | Bowen Xu | Yunhao Song

(2023)

Collaborative optimization of linear vibrating screen screening efficiency and dynamic response stability based on coupled DEM-MBK simulation

(2023)

Dynamic characteristics analysis of a novel vibrating screen based on electromechanical coupling simulation

Zhenqian Wang | Jida Wu | Zhaojun Kou | Yuanming Zhang | Chusheng Liu

(2023)

Research on dynamic and vibration behaviors of a flip-flow screen with crankshaft-link structure

Hongxi Li | Chusheng Liu | Enhui Zhou | Ling Shen

(2022)

Research on the mechanism of equal-thickness screening process formation of banana-type vibrating screens based on the signal analysis of the wavelet packet energy spectrum

(2022)

Research of the Collision Mechanics Model and Time-Frequency Characteristics during the Multistage Variable-Inclination Screening Process for Clean Coal

(2022)

Kinematics characteristics of the flip-flow screen with a crankshaft-link structure and screening analysis for moist coal

Hongxi Li | Chusheng Liu | Ling Shen | Lala Zhao | Sai Li

(2021)

Analysis of the dynamic forces acting on a vibrating screen and its support structure using a scale model

Thiago Bento Linhares | Claysson Bruno Santos Vimieiro

(2021)

Research on impact characteristics of screening coals on vibrating screen based on discrete-finite element method

(2020)

Dynamic Modeling and Parameters Optimization of Large Vibrating Screen with Full Degree of Freedom

Xiaodong Yang | Jida Wu | Haishen Jiang | Wenqiang Qiu | Chusheng Liu

(2019)

A review on the advanced design techniques and methods of vibrating screen for coal preparation

(2019)

Impact of screening coals on screen surface and multi-index optimization for coal cleaning production

Zhenqian Wang | Chusheng Liu | Jida Wu | Haishen Jiang | Yuemin Zhao

(2018)

About this article

Received

09 March 2017

Accepted

20 September 2017

Published

31 December 2017

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2017.18319

Keywords

large vibrating screen

duplex statically indeterminate mesh beam structure

dynamic theoretical model

finite element method

high strength

Acknowledgements

The research work is financially supported by the National Natural Science Foundation of China (Nos. U1508210, 51620105001, 51775544), Jiangsu Province Research Prospective Project (No. BY2015023-01).

Author Contributions

Liu conceived and designed the experiments. Wang, Wu, Jiang and Song performed the experiments. Wang analyzed the data and wrote the manuscript. Zhao helped perform the analysis with constructive discussions.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 03 14

Dynamic characteristics analysis of a novel vibrating screen based on electromechanical coupling simulation

Zhenqian Wang, Jida Wu, Zhaojun Kou, Yuanming Zhang, Chusheng Liu

Research article

2023 02 11

Dynamic characteristics analysis of a circular vibrating screen

Yuanchen Wang, Zhenqian Wang, Min Zhang, Bowen Xu, Yunhao Song

Research article

2022 08 15

Research on dynamic and vibration behaviors of a flip-flow screen with crankshaft-link structure

Hongxi Li, Chusheng Liu, Enhui Zhou, Ling Shen

Research article

2020 05 15

Particle stratification of a vibrating screen with translation-swing composite motion

Guolang Shen, Xin Tong

Z. Wang, C. Liu, J. Wu, H. Jiang, B. Song, and Y. Zhao, “A novel high-strength large vibrating screen with duplex statically indeterminate mesh beam structure,” Journal of Vibroengineering, Vol. 19, No. 8, pp. 5719–5734, Dec. 2017, https://doi.org/10.21595/jve.2017.18319

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2017.18319
UR  - https://doi.org/10.21595/jve.2017.18319
TI  - A novel high-strength large vibrating screen with duplex statically indeterminate mesh beam structure
T2  - Journal of Vibroengineering
AU  - Liu, Chusheng
AU  - Wang, Zhenqian
AU  - Wu, Jida
AU  - Jiang, Haishen
AU  - Song, Baocheng
AU  - Zhao, Yuemin
PY  - 2017
DA  - 2017/12/31
PB  - JVE International Ltd.
SP  - 5719-5734
IS  - 8
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Liu_2017,
	doi = {10.21595/jve.2017.18319},
	url = {https://doi.org/10.21595/jve.2017.18319},
	year = 2017,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {8},
	pages = {5719--5734},
	author = {Chusheng Liu and Zhenqian Wang and Jida Wu and Haishen Jiang and Baocheng Song and Yuemin Zhao},
	title = {A novel high-strength large vibrating screen with duplex statically indeterminate mesh beam structure},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]C. Liu, Z. Wang, J. Wu, H. Jiang, B. Song, and Y. Zhao, “A novel high-strength large vibrating screen with duplex statically indeterminate mesh beam structure,” Journal of Vibroengineering, vol. 19, no. 8, pp. 5719–5734, Dec. 2017, doi: 10.21595/jve.2017.18319.

Copy IEEE

Copied to clipboard!

Liu, Chusheng, Zhenqian Wang, Jida Wu, Haishen Jiang, Baocheng Song, and Yuemin Zhao. “A Novel High-Strength Large Vibrating Screen with Duplex Statically Indeterminate Mesh Beam Structure.” Journal of Vibroengineering 19, no. 8 (December 31, 2017): 5719–34. https://doi.org/10.21595/jve.2017.18319.

Copy Chicago

Copied to clipboard!

A novel high-strength large vibrating screen with duplex statically indeterminate mesh beam structure

Abstract

1. Introduction

2. Comparison of structure between VSDSIMBS and TVS

3. Dynamic model calculation of VSDSIMBS

3.1. Calculation of stiffness

3.2. Calculation of characteristic parameters

4. Comparison between VSDSIMBS and TVS by FE method

4.1. Modal analysis of VSDSIMBS and TVS

4.2. Harmonic response analysis of VSDSIMBS and TVS

5. Full-scale experimental tests on VSDSIMBS and comparisons between simulation results and test results

6. Conclusions

References

Cited by

About this article

Related Articles