Residential comfort assessment due to blasting vibration

Yao, Qiang; Yang, Xingguo; Li, Hongtao

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 March 2014

Check for updates

Residential comfort assessment due to blasting vibration

Qiang Yao¹

Xingguo Yang²

Hongtao Li³

^{1, 2, 3}School of Water Resource and Hydropower, Sichuan University, Chengdu, 610065, China

^{2, 3}State Key Lab. of Hydraulics and Mountain River Eng., Sichuan University, Chengdu, 610065, China

Corresponding Author:

Hongtao Li

Cite the article Download PDF

Downloads 1155

Abstract

Blasting operation usually causes vibration to adjacent buildings and adversely impacts the residential comfort of residents, and the resulting disturbance to residents may lead to the occurrence of disputes and complaints against such problems. In this study, the blasting vibration acceleration is calculated based on the measured blasting vibration velocity signal using the four-point forward difference method. The Infinite Impulse Response (IIR) digital filter is applied for frequency weighting of acceleration, so as to calculate the comfort index; the vibration dose value (VDV) method is adopted to evaluate the vibration comfort and impact of blasting operation. Combined with engineering cases analyses, it is found that even small blasting vibrations which are insufficient to cause building damage might result in residents’ grumbles or complaints, and thus we suggests that the comfort of blasting vibration be taken into account during blasting operations.

1. Introduction

Blasting operation usually results in obvious ground vibration which, if too excessive, will not only cause damage to surrounding buildings, but also adversely impact the residential comfort of residents living in these buildings and result in their discontents. With the wide application of blasting technology, disputes and complaints caused by the blasting seismic effects become increasingly intensified, and mostly focus on building damage issues like wall cracking, blasting noise and vibration disturbance to residents. Literature surveys have indicated that, the essence of most cases involves a typical vibration comfort issue rather than a safety issue [1-3]. In other words, such an issue is actually manifested as the overreactions of residents in the case of their personal and property interests being threatened by blasting vibration. In order to evaluate the impact of blasting operation on the vibration comfort of buildings, it is necessary to establish a set of methodology to assess the blasting vibration comfort in the residential area.

The earliest systematic study on the response of the human body to a vibration environment was conducted by Wilhelm Wundt from Germany [4]. After that, scholars from the United Kingdom, Germany, and the United States, etc. carried out numerous studies and acquired a great deal of achievements, gradually leading to a series of international standard [5-8]. These research achievements have already been systematically summarized by Griffin in his work [9]. However, Blasting vibration is a transitory phenomenon lasting for a second or so. The literature related to the response of the human body to blasting vibration is very limited. Hendron and Oriard [10] gave an account of people’s perceptions and their responses to impulse vibrations. Wiss and Paramelee [11] demonstrated that the human response to transitory vibrations was related to damping of the motion rather than the frequency. Siskind et al. [12] correlated the response with human annoyance. Walter and Walter [13] described a subjective assessment of human behavior and ground vibrations. Heggie [14] compared other vibrations to those produced by blasting. St. George [15] conducted investigations on community responses to blasting vibrations. Kuzu and Guclu [16] studied the responses of people to blasting vibrations in tunnel construction. The present study is an initial attempt to evaluate the responses of people residing near sources of explosions. The four-point forward difference method is used to calculate the blasting vibration acceleration based on actual measurement of the blasting vibration velocity signal. The acceleration signal is then weighted by frequency using IIR digital filter to analyze and calculate the vibration comfort index of people in a standing posture and two prone postures (supine and lateral positions), and the impact of blasting operation on the comfort of residential area is evaluated through VDV method.

2. Ascertainment of blasting vibration acceleration

Currently the monitoring of blasting vibration is for the most part the monitoring of vibration velocity. It is of significant importance to obtain a reliable vibration acceleration based on the measured blasting vibration velocity for the calculation of the vibration comfort index. Blasting vibration is an aperiodic transient motion process. According to the relationship between the acceleration and velocity, the particle acceleration process can be calculated by differentiating the particle velocity process. The amplitude and time of the particle vibration velocity signal obtained in the process of blasting vibration monitoring are both continuous numerical values, and the acceleration value at any instant can be calculated by the differential equation below:

1

a (t) = \frac{d v (t)}{d t} .

Currently blasting tests are generally recorded in the form of digital signals. Given that both the time and amplitude are discrete data, the numerical differentiation method can be employed to calculate the acceleration process:

2

a (t_{i}) = \frac{Δ v (t_{i})}{Δ t_{i}} = \frac{v (t_{i + 1}) - v (t_{i})}{t_{i + 1} - t_{i}} .

Since the digitally corrected velocity data are unavoidably subject to random errors, when $Δ v (t_{i}) = v (t_{i + 1}) - v (t_{i})$ is very small, the acceleration value calculated by Equation (2) appears to be very sensitive even to small errors. In order to reduce errors and improve the calculation precision, a differential method is adopted to calculate the acceleration of the discrete data. In this paper, Four-point forward difference method is employed as indicated by Equation (3):

3

a (t_{i}) = \frac{2 v (t_{i + 3}) - 9 v (t_{i + 2}) + 18 v (t_{i + 1}) - 11 v (t_{i})}{6 Δ t},

where $Δ t$ is the sampling interval of blasting vibration, (s).

When Equation (3) is used for numerical differential calculation, its truncation error is represented as:

4

E \approx - \frac{1}{4} {(Δ t)}^{3} v^{(4)} (t) .

The truncation error of four-point forward difference scheme is four-order and its value is in direct proportion to the value of ${(Δ t)}^{3}$ , so it will rapidly decrease with the decrease of the sampling interval $Δ t$ . Hence, when blasting vibration velocity data are used to ascertain the acceleration, in order to improve the calculation accuracy, an appropriate sampling frequency should be adopted under the premise of taking into consideration the data storage capacity of the recording instrument and the duration of the entire blasting vibration.

Due to the high-frequency components induced by data errors, the waveform of the acceleration curve calculated by Equation (3) is seriously distorted. In order to obtain an ideal waveform of blasting vibration acceleration, the wavelet analysis method is employed to eliminate the high-frequency noise component of acceleration waveform. Wavelet decomposition of the acceleration waveform obtained through the direct differentiation can display various frequency components in the signal; if effective signals and noise signals residing in various frequency band ranges can be better separated, an ideal acceleration waveform will be acquired as a result. The key to wavelet analysis lies in the selection of wavelet basis function and the determination of decomposition layer number. As the blasting vibration signal is a random signal, the wavelet basis function frequently used in nonstationary vibration signal analysis currently is db8 wavelet basis function [17-18]; the decomposition scale (layer number) needs to be determined based on the signal sampling frequency, effective blasting vibration frequency and noise signal frequency component.

Suppose that the sampling frequency of blasting vibration signal is $f_{1}$ , the effective frequency range of blasting vibration is $0 ~ f_{2}$ and the minimum frequency of noise signal is $f_{3}$ , then the signal analysis frequency range will be $0 ~ f_{1} / 2$ , and the noise frequency range will be $f_{3} ~ f_{1} / 2$ . According to wavelet analysis theory, when $n$ -layer decomposition is conducted on acceleration waveform data, the frequency band range of low frequency coefficient of scale $n$ is $0 ~ \frac{f_{1} / 2}{2^{n}}$ . In order to eliminate the high-frequency noise from the low-frequency component obtained through decomposition without losing any effective signal, the following condition must be satisfied:

5

f_{2} \leq \frac{f_{1} / 2}{2^{n}} \leq f_{3} .

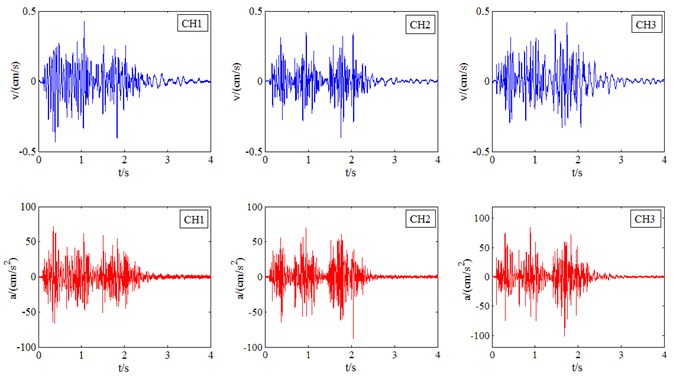
In terms of the blasting vibration signal in the present study, the sampling frequency and the effective frequency range of the blasting vibration signal are respectively 5.000 Hz and 0-150 Hz, while the frequency range of noise signal is 500-2.500 Hz. According to Equation (5), the rational layer number of wavelet decomposition is three or four. Based on the above method, an accurate and clear acceleration time-history curve can be obtained. Fig. 1 shows the vibration velocity and transformed acceleration time-history curves of #6 (see Table 4) in the case analyzed in the present study (vertical direction CH1, horizontal radial direction CH2 and horizontal tangential direction CH3).

Fig. 1Recorded velocity and transformed acceleration time-history

3. Assessment method of vibration comfort

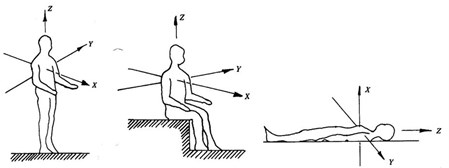
For the human body, different postures correspond to different physiological coordinates. The level of vibration that inputs into the human body and the perception degree of the human body for vibrations with the same intensity can vary with coordinates, so the posture of the human body should be taken into account when assessing vibration comfort [7]. The physiological coordinate axes of the human body in three common postures are shown in Fig. 2, and the origin of coordinates is set at the part where vibration is input into the human body. We carried out the calculation in terms of some postures the human body is most likely in (standing, supine and lateral) when blasting vibration occurs.

Fig. 2Human basic axis of coordinates

According to the international standards ISO-2631 and BS-6841 on the response of the human body to vibration, various frequency-weighted functions are employed to represent the differences in perceptions of the human body for vibration signals at different frequencies. In this case the vibration acceleration needs to go through a filtering processing, so as to decompose the original signal by frequency into various directions of physiological coordinate axis. As for the method for frequency weighting of vibration signal, international standards [5-8] provide frequency-domain filtering weighting methods such as overall frequency weighting and 1/3 bandwidth frequency weighting. However, as the velocity and acceleration obtained in practice are both digital signals within the time domain, the time-domain vibration signals firstly need to be transformed into frequency-domain signals before use, thereby increasing the processing complexity. With the purpose of overcoming such an inadequacy, we adopted the time-domain digital filter (IIR digital filter), which is represented by the following equation [19-20]:

6

a_{f} (t_{i}) = \frac{1}{c_{0}} [\sum_{k = 0}^{M} b_{k} a (t_{i - k}) - \sum_{j = 1}^{N} c_{j} a_{f} (t_{i - j})],

where $a (t)$ is the vibration acceleration signal before frequency weighting, $a_{f} (t)$ is the vibration acceleration signal after frequency weighting, and $M$ is the number of zeros, set at 2; $N$ is the number of poles, set at 2; both $b_{k}$ and $c_{j}$ are the filter coefficients.

An IIR filter uses previous output values in addition to previous input values to calculate the current output sample value. When employing the Equation (6) which represents the infinite impulse response (IIR) digital filter, the first move is to determine the six filter coefficients ( $c_{0}$ , $c_{1}$ , $c_{2}$ , $b_{0}$ , $b_{1}$ and $b_{2}$ ), and then they can be used to calculate the frequency-weighted vibration acceleration $a_{f}$ . The method for calculating the filter coefficients is given below.

The filters defined in ISO 2631 comprise a number of sections, which are defined as analogue transfer functions and then cascaded in different combinations to produce the total weighting filters. In the component filter sections, band-limiting is performed using filters labelled as ‘high-pass’ and ‘low-pass’; the frequency-weighting filter parts of the process are achieved using ‘acceleration-velocity transition’ and ‘upwards step’ filters. These can be expressed in the $s$ -domain as follows.

High-pass filter:

7

H_{h} (s) = \frac{s^{2}}{s^{2} + \frac{ω_{1}}{Q_{1}} s + ω_{1}^{2}} .

Low-pass filter:

8

H_{l} (s) = \frac{ω_{2}^{2}}{s^{2} + \frac{ω_{2}}{Q_{2}} s + ω_{2}^{2}} .

Acceleration-velocity transition filter:

9

H_{t} (s) = \frac{\frac{ω_{4}^{2}}{ω_{3}} s + ω_{4}^{2}}{s^{2} + \frac{ω_{4}}{Q_{4}} s + ω_{4}^{2}} .

Upward step filter:

10

H_{S} (s) = \frac{s^{2} + \frac{ω_{5}^{2}}{Q_{5}} s + ω_{5}^{2}}{s^{2} + \frac{ω_{6}}{Q_{6}} s + ω_{6}^{2}},

where $ω = 2 π f$ ; values of $f$ and $Q$ are shown in Table 1. Corresponding to the physiological coordinates of the human body, ISO 2631 uses the frequency-weighted functions of the vertical $Z$ axis ( $W_{k}$ ) and the horizontal $X$ - $Y$ axis ( $W_{d}$ ) to represent the differences in the perceptions of human body for vibration signals at different frequencies, where $W_{d} = H_{h} (s) \cdot H_{l} (s) \cdot H_{t} (s)$ and $W_{k} = H_{h} (s) \cdot H_{l} (s) \cdot H_{t} (s) \cdot H_{s} (s)$ .

Table 1Numeric values to be used in Equations (7)-(10)

	$H_{h}$		$H_{l}$		$H_{t}$			$H_{s}$
	$f_{1}$	$Q_{1}$	$f_{2}$	$Q_{2}$	$f_{3}$	$f_{4}$	$Q_{4}$	$f_{5}$	$f_{6}$	$Q_{5}$	$Q_{6}$
$W_{k}$	0.4	$1 / \sqrt{2}$	100	$1 / \sqrt{2}$	12.5	12.5	0.63	2.37	3.35	0.91	0.91
$W_{d}$	0.4	$1 / \sqrt{2}$	100	$1 / \sqrt{2}$	2	2	0.63	–	–	–	–

There are several methods for deriving a digital filter from an analogue filter. The bilinear transformation method with frequency warping is used in this paper. In the bilinear transformation method of the digital IIR filter design, $s$ in the analogue $s$ -domain equation is replaced by the bilinear transformation defined by Equation (11):

11

s \to 2 \frac{(1 - z^{- 1})}{(1 + z^{- 1})} .

There is, however, a non-linear relationship between the digital frequency and the analogue frequency. Pre-warping of the frequencies used in the analogue $s$ -domain equations (with the substitution shown in Equation (12)) can eliminate this problem:

12

ω_{n}^{'} \to 2 t a n [\frac{ω_{n}}{2}],

where $ω_{n}$ is the normalised filter design frequency (i.e. $2 π f_{c} / f_{s}$ , where $f_{c}$ is the centre frequency and $f_{s}$ is the sampling frequency) and $ω_{n}^{'}$ is the normalised warped frequency. To design the equivalent digital IIR filter, Equation (11) is substituted into the analogue $s$ -domain equation (Equations (7)-(10)), which is simplified until it is in the form of Equation (13):

13

H (z) = \frac{b_{2} z^{- 2} + b_{1} z^{- 1} + b_{0}}{c_{2} z^{- 2} + c_{1} z^{- 1} + c_{0}} .

Based on the above method, both $b_{k}$ and $c_{j}$ can be calculated by Table 2. The parameters ( $A$ , $B$ , $C$ , $D$ , $E$ and $F$ ) in Table 2 respectively represent the forms of filtered frequencies in the frequency filter after warping, and can be collectively expressed as $φ_{i} = t a n (π f_{c i} / f_{s})$ , where $f_{c i}$ is the central frequency of each filter, i.e., respectively assigned by $f_{1} ~ f_{6}$ in Table 1; $f_{s}$ represents the sampling frequency.

Table 2Summary of filter coefficients

The filter coefficients	$H_{h}$	$H_{l}$	$H_{t}$	$H_{s}$
$b_{2}$	$2 \sqrt{2} B^{2}$	$2 \sqrt{2} B^{2}$	$2.52 C^{2} - 2.52 C^{2} / D$	$4 E^{2} - 4.396 E + 4$
$b_{1}$	– $4 \sqrt{2}$	$4 \sqrt{2} B^{2}$	$5.04 C^{2}$	$8 E^{2} - 8$
$b_{0}$	$2 \sqrt{2}$	$2 \sqrt{2} B^{2}$	$2.52 C^{2} / D + 2.52 C^{2}$	$4 E^{2} + 4.396 E + 4$
$c_{2}$	$2 \sqrt{2} - 4 A + 4 A^{2}$	$2 \sqrt{2} - 4 B + 2 \sqrt{2} B^{2}$	$2.52 - 4 C + 2.52 C^{2}$	$4 F^{2} - 4.396 F + 4$
$c_{1}$	$8 A^{2} - 4 \sqrt{2}$	$4 \sqrt{2} B^{2} - 4 \sqrt{2}$	$5.04 C^{2} - 5.04$	$8 F^{2} - 8$
$c_{0}$	$2 \sqrt{2} + 4 A + 4 A^{2}$	$2 \sqrt{2} + 4 B + 2 \sqrt{2} B^{2}$	$2.52 + 4 C + 2.52 C^{2}$	$4 F^{2} + 4.396 F + 4$

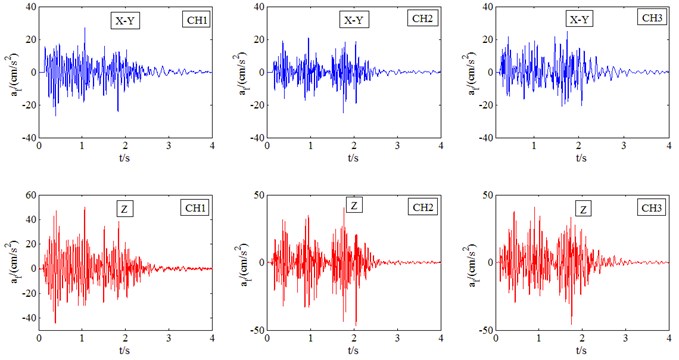
The sampling frequency $f_{s}$ in the paper is 5.000 Hz; based on Table 1 and Table 2, various filter coefficients can be calculated out, as indicated in Table 3. As for the judgment of vibration comfort in various postures, $W_{k}$ and $W_{d}$ are respectively employed to execute the frequency weighting of vibration signal in the vertical direction ( $Z$ axis) and the horizontal direction ( $X$ - $Y$ axis). The transformed accelerations were frequency weighted by applying Eq. (6). First the vibration signal was passed through the band-limiting filter and then the resulting signal was passed through the frequency-weighting filter. The time-history curves of the vibration accelerations in three directions in Fig. 1 after frequency weighting in the vertical direction ( $Z$ axis) and the horizontal direction ( $X$ - $Y$ axis) are given in Fig. 3.

Table 3Summary of filter coefficients in the case

The filter coefficients	$W_{d}$ ( $X$ - $Y$ axis)			$W_{k}$ ( $Z$ axis)
The filter coefficients	$H_{h}$	$H_{l}$	$H_{t}$	$H_{h}$	$H_{l}$	$H_{t}$	$H_{s}$
$b_{2}$	2.828427	0.011184	–0.003161	2.828427	0.011184	-0.019627	3.993468
$b_{1}$	–5.656854	0.022369	0.000008	–5.656854	0.022369	0.000311	–7.999982
$b_{0}$	2.828427	0.011184	0.003169	2.828427	0.011184	0.019937	4.006550
$c_{2}$	2.827422	2.588079	2.514980	2.827422	2.588079	2.488755	3.990769
$c_{1}$	–5.656853	–5.634486	–5.039992	–5.656853	–5.634486	–5.039690	–7.999965
$c_{0}$	2.829432	3.091143	2.525028	2.829432	3.091143	2.551555	4.009267

Having obtained the frequency-weighted acceleration signal $a_{f} (t)$ , the paper can go on to calculate the vibration comfort assessment indexes. The commonly-used three kinds of assessment indexes include root mean square value of acceleration (ms^-2) (r.m.s.), estimated vibration dose value (ms^-1.75) ( $e V D V$ ) and $V D V$ (ms^-1.75), and can be calculated respectively by the three equations below [9]:

14

a_{f r m s} = {[\frac{1}{N_{s}} \sum_{i = 1}^{N_{s}} a_{f i}^{2}]}^{\frac{1}{2}},

15

e V D V = {[T_{s} {(1.4 a_{f r m s})}^{4}]}^{\frac{1}{4}},

16

V D V = {[\frac{T_{s}}{N_{s}} \sum_{i = 1}^{N_{s}} a_{f i}^{4}]}^{\frac{1}{4}},

where $a_{f r m s}$ , $V D V$ and $e V D V$ are the root mean square of acceleration, the vibration dose value and the estimated vibration dose value, respectively; $a_{f} (t)$ is the weighted time-history function of vibration acceleration; $N_{s}$ and $T_{s}$ are the sample point numbers of vibration duration and acceleration time-history, respectively.

Fig. 3Time history of transformed acceleration after frequency weighting of Z or X-Y axis

Since the blasting vibration proceeds simultaneously on three directions ( $X$ axis, $Y$ axis and $Z$ axis), the overall effect of vibrations in the three directions should be comprehensively taken into account in vibration comfort assessment, and can be converted into a unidirectional ( $Z$ axis) effect by the following equations [9]:

17

\bar{a_{f}} = {[1.4 a_{f r m s x})^{2} + {(1.4 a_{f r m s y})}^{2} + {(a_{f r m s z})}^{2}]}^{\frac{1}{2}},

18

\bar{e V D V} = {[{(1.4 e V D V_{x})}^{4} + {(1.4 e V D V_{y})}^{4} + {(e V D V_{z})}^{4}]}^{\frac{1}{4}},

19

\bar{V D V} = {[{(1.4 V D V_{x})}^{4} + {(1.4 V D V_{y})}^{4} + {(V D V_{z})}^{4}]}^{\frac{1}{4}},

where $a_{f r m s x}$ , $a_{f r m s y}$ and $a_{f r m s z}$ are the weighted root mean square accelerations of $X$ axis, $Y$ axis and $Z$ axis respectively; $V D V_{x}$ , $V D V_{y}$ and $V D V_{z}$ are the vibration dose values of $X$ axis, $Y$ axis and $Z$ axis respectively; $\bar{a_{f}}$ is the converted total weighted root mean square acceleration; $\bar{e V D V}$ and $\bar{V D V}$ are the converted total estimated vibration dose value and the converted total vibration dose value respectively.

4. Assessment case of blasting vibration comfort

During the blasting operation of a hydropower project, we conducted the monitoring of blasting vibration velocity in an adjacent building. The monitoring instrument was installed on the ground of the first floor of the building, and could simultaneously monitor three directions. In the case analysis, buildings basically are given priority to with 1 $~$ 2 layer bungalow. In the blasting vibration monitoring and investigation of the respondents’ feeling of blasting vibration, respondents were all in the ground floor of buildings, blasting vibration monitoring points were also in the ground floor of buildings in close proximity to the respondents. Assumes that the blasting vibration monitoring data was the perceived vibration of human body, and the process of blasting seismic wave spreading to the human body through the soil-rock medium and buildings is very complicated, which is not the research emphasis in this paper. Therefore, the authors try to avoid and simplify the problem, and highlight the adverse impact of blasting vibration on the feelings of people. Multiple groups of blasting vibration monitoring data were obtained thereby. Statistical analysis showed that, the peak particle vibration velocity (PPV) is concentrated in 0.11-0.82 cm/s, the duration concentrated in 0.56-1.12 s, and the main vibration frequency is concentrated in 10-40 Hz. Based on provisions of the national standard Safety Regulations for Blasting Practice (GB6722-2003), the blasting vibration (PPV $\leq$ 2 cm/s) would not cause damage to local residential buildings (brick-concrete structured); the field observation also proved that no damage was caused to buildings. The case here falls exactly into the category of typical cases involving blasting vibration comfort issue instead of safety issue.

In the vibration comfort analysis, 14 groups of representative measured velocity data of blasting vibration were selected and numbered as 1#~14# (Table 4). The vibration comfort doses perceived by the human body were calculated in terms of three common postures (standing, supine and lateral). Given that blasting vibration spread simultaneously towards three directions, it would be more realistic to consider the whole effect of vibration in the three directions. The total effect of vibration in the three directions for human postures was calculated, as listed in Table 4. The assessment of vibration comfort was conducted according to ISO2631-2. The blasting was operated during daytime, and the limit multiple defined by ISO2631-2 in daytime is two to four times of the datum acceleration for the residential areas close to the blasting source, so for vibration in $Z$ axis direction, the datum acceleration was set at 0.005 m/s²; for vibration in $X$ - $Y$ axis direction, the datum acceleration was set at 0.0036 m/s². According to the calculation results most of the blasting vibration accelerations ( $a_{f r m s}$ ) exceed the required values provided in ISO2631-2.

In field comfort survey, the responses of residents were recorded and divided into three levels, i.e., no obvious response (A), moderate response (B) and intense response (C). “No obvious response” means that the blasting vibration neither significantly disturbs the daily life of residents nor terminates their activities in progress; “Moderate response” means that the residents are prevented from continuing their activities, and are interfered and scared, and even complain of such prevention. “Intense response” means that residents get together to stop the blasting operation and other critical cases. See the survey results in Table 4.

Based on the analysis of weighted root mean square acceleration, it can be determined that the vibration is beyond the demand of the vibration comfort standard. $V D V$ and the times ( $N_{t}$ ) of reaching the designated vibration dose value level ( $V D V_{t}$ ) were combined to further estimate the impact degree of vibration on residents. This method was firstly introduced by Griffin to assess the overall impact of continuous repeated vibrations on the vibration comfort of buildings. Table 5 shows various $V D V_{t}$ levels and degrees of resident complaints hereby caused [9].

The times ( $N_{t}$ ) of reaching the designated vibration dose value level ( $V D V_{t}$ ) can be calculated by the equation below [9]:

20

N_{t} = {[\frac{V D V_{t}}{V D V_{i}}]}^{4},

where $V D V_{i}$ is the $V D V$ value of one vibration event. In combination with the calculation results provided in Table 4, the vector sum in three directions is employed to assess the comfort perceived by people in various postures and positions. As shown in Table 4, the calculation result of $V D V$ is between 0.03 to 0.442; when $V D V$ reaches or exceeds 0.217, conducting blasting operation once may cause the discontents of residents. Evidently, for the blasting operation in the present case, which is a continuous repeated operation conducted twice a day and carried on for months, it will impose a great impact on the vibration comfort of residents based on the division method proposed by Grinffin regarding its comfort impact on buildings [9].

Table 4Calculation results of vibration comfort doses and results of field survey

No.	Channel	$P P V$ (cms^-1)	Principal vibration frequency (Hz)	Time (s)	Posture	$\bar{a_{f}}$ (ms^-2)	$\bar{e V D V}$ (ms^-1.⁷⁵)	$\bar{V D V}$ (ms^-1.75)	Survey results
1#	CH1	0.22	18.9	1.5	Standing	0.0221	0.0297	0.0337	A
	CH2	0.10	27.2		Supine	0.0275	0.0391	0.0589	A
	CH3	0.14	17.8		Lateral	0.0300	0.0404	0.0591	A
2#	CH1	0.20	34.5	1.2	Standing	0.0223	0.0295	0.0309	A
	CH2	0.30	20.9		Supine	0.0319	0.0442	0.0496	A
	CH3	0.25	29.4		Lateral	0.0200	0.0266	0.0294	A
3#	CH1	0.31	17.9	1.6	Standing	0.0350	0.0531	0.0529	A
	CH2	0.16	31.2		Supine	0.0264	0.0367	0.0373	A
	CH3	0.39	27.4		Lateral	0.0496	0.0763	0.0738	A
4#	CH1	0.28	18.9	1.3	Standing	0.0385	0.0541	0.0571	A
	CH2	0.37	24.8		Supine	0.0393	0.0572	0.0634	A
	CH3	0.41	31.5		Lateral	0.0333	0.0456	0.0523	A
5#	CH1	0.43	20.2	1.5	Standing	0.0684	0.1046	0.1018	A
	CH2	0.39	23.7		Supine	0.0475	0.0687	0.0689	A
	CH3	0.45	26.5		Lateral	0.0402	0.0563	0.0609	A
6#	CH1	0.45	23.0	2.8	Standing	0.0704	0.1104	0.1074	B
	CH2	0.41	26.0		Supine	0.0539	0.0811	0.0834	A
	CH3	0.46	23.5		Lateral	0.0411	0.0620	0.0627	A
7#	CH1	0.66	20.0	0.95	Standing	0.0568	0.0780	0.1005	B
	CH2	0.68	22.0		Supine	0.0494	0.0676	0.0964	B
	CH3	1.15	20.8		Lateral	0.0533	0.0729	0.1174	B
8#	CH1	0.78	19.8	0.9	Standing	0.0520	0.0675	0.0811	B
	CH2	0.82	14.7		Supine	0.0517	0.0673	0.0824	B
	CH3	1.15	31.7		Lateral	0.0529	0.0691	0.0785	B
9#	CH1	1.33	37.0	1.2	Standing	0.0976	0.1422	0.1836	B
	CH2	1.19	7.5		Supine	0.0862	0.1249	0.1575	B
	CH3	0.82	27.0		Lateral	0.0490	0.0684	0.0930	B
10#	CH1	0.91	29.6	0.6	Standing	0.1022	0.1246	0.1697	B
	CH2	1.18	12.6		Supine	0.0901	0.1103	0.1554	B
	CH3	0.98	15.1		Lateral	0.0775	0.0934	0.1300	B
11#	CH1	1.07	20.4	1.1	Standing	0.0860	0.1214	0.1500	B
	CH2	1.73	23.5		Supine	0.1235	0.1764	0.2533	B
	CH3	1.06	32.6		Lateral	0.0570	0.0786	0.1011	B
12#	CH1	0.83	22.2	0.7	Standing	0.0840	0.1050	0.1509	C
	CH2	2.20	16.1		Supine	0.2047	0.2615	0.3688	C
	CH3	2.03	26.3		Lateral	0.1196	0.1515	0.2141	C
13#	CH1	3.05	32.5	0.5	Standing	0.1897	0.2221	0.3206	C
	CH2	3.17	33.9		Supine	0.1801	0.2103	0.3948	C
	CH3	3.36	18.3		Lateral	0.2062	0.2421	0.3276	C
14#	CH1	2.73	15.4	0.4	Standing	0.1925	0.2132	0.3220	C
	CH2	3.90	11.6		Supine	0.2836	0.3153	0.4419	C
	CH3	3.05	14.1		Lateral	0.1480	0.1628	0.2656	C

Table 5Resident response to different levels of VDVs

$V D V_{t}$ / ms^-1.75	< 0.108	< 0.217	< 0.434	< 0.868
Possibility of resident complaint	Very rare	Rare	Frequent	Very frequent

ISO10137 [21] defines the possibilities of resident complaint corresponding to $V D V$ for assessment, namely, 0.2-0.4 (low possibility of resident complaint), 0.4-0.8 (moderate possibility of resident complaint) and 0.8-1.6 (high possibility of resident complaint). It can be seen from Table 4 that, the $V D V_{s}$ are uniformly less than 2 and basically concentrate between 0.03 and 0.442. When this assessment method is employed, a conclusion of “low possibility of resident complaint” can be obtained.

It is clear that, employing different vibration comfort assessment standards will result in different or even contrary conclusions. Since blasting vibration features of high amplitude, high frequency and short duration, it is worth discussing and studying the determination of comfort assessment standards applicable for blasting vibration and the true feelings of residents for blasting vibration. In view of this, we conducted a field survey on the true feelings of residents (which are recorded by three types, namely, no obvious response, general response and intense response) during the monitoring process of blasting vibration. The survey which involves hundreds of respondents shows that, when the value of $V D V$ is less than 0.1, the residents basically show no obvious response (A); when the value of $V D V$ is greater than 0.1 and less than 0.2, a few residents show obvious responses (B); when the value of $V D V$ is greater than 0.2, the discontents and responses of residents become more intense (C). Besides, the $V D V$ value changes insignificantly with human postures, which, combined with the fact that the residents with different postures basically respond consistently to the same blasting, suggests that the impact of different human postures on blasting vibration comfort is insignificant, or in other words that no such a posture exists that is especially “sensitive” to blasting vibration. This may can be explained by the fact that blasting vibration is a kind of transient impact vibration.

Based on the calculation results of $V D V$ provided in Table 4, $V D V$ value increases with the intensity of vibration. When the $P P V$ is less than 0.5 cm/s, $V D V$ is basically less than 0.1; when the PPV is larger than 0.5 cm/s and less than 1.0 cm/s, $V D V$ is mainly less than 0.2; with the continuous increase of vibration intensity, $V D V$ will also increase, which will further cause obvious adverse impact on the residence comfort, but probably no damage is caused to buildings at this point. United States Bureau of Mines (USBM) once analyzed the impact of blasting vibration and similar vibrations on people, finding that when the $P P V$ of vibration reaches to 5 mm/s, the complaint rate can reach to 5 %; when the $P P V$ reaches to 10 mm/s, the complaint rate can reach to 10 % [12], which is similar to the conclusions obtained in this paper. And more blasting vibration comfort cases analysis results also verify the reliability of the conclusions obtained in this paper. It also can be concluded that, the vibration intensity satisfying blasting vibration comfort should be less than the safety limit of structural damage.

5. Conclusions

With regard to the blasting vibration comfort issue, the paper discussed the assessment methods and standards of blasting vibration comfort through the blasting vibration monitoring, analytic calculation and field survey. It is proposed that the acceleration can be calculated based on the measured blasting vibration velocity by using the wavelet denoising-based four-point forward difference method. Case analysis shows that, when the value of $V D V$ is less than 0.1, the residents basically show no discontents; when the value of $V D V$ is greater than 0.1 and less than 0.2, a few residents show obvious responses; when the value of $V D V$ is greater than 0.2, the discontents and responses of residents become more intense. The impact of different human postures on blasting vibration comfort is insignificant. Vibration intensity satisfying blasting vibration comfort is less than the safety limit of structural damage. During the construction of a hydropower project, resident complaint is a commonly-seen factor that affects the normal construction progress and causes additional project expenses. Therefore, it is suggested that, under the premise of guaranteeing normal and safe construction, equal importance should be attached to the blasting vibration comfort issue during the blasting operation.

References

Raina A. K., Haldar A., Chakraborty A. K., et al. Human response to balst-induced vibration and air-overpressure: an indian scenario. Bull. Eng. Geol. Env., Vol. 63, 2004, p. 209-214.

Search CrossRef
Randall K. N. Forensic engineering investigation. New York, CRC Press, 2001.

Search CrossRef
Xia Y., Nassif H., Hwang E. S., Linzell D. Optimization of design details in orthotropic steel decks subjected to static and fatigue loads. Transportation Research Record: Journal of the Transportation Research Board, Vol. 2331, 2013, p. 14-23.

Search CrossRef
Wundt W. Lectures on human and animal psychology. Bel Air, Read Books, 2007.

Search CrossRef
BS 6841 Guide to measurement and evaluation of human exposure to whole-body mechanical vibration and repeated shock. British Standards Institution, London, 1987.

Search CrossRef
ISO 2631 Mechanical vibration and shock-evaluation of human exposure to whole-body vibration. Part 1: general requirement. International Organization for Standardization, Geneva, 1997.

Search CrossRef
ISO 2631 Mechanical vibration and shock-evaluation of human exposure to whole-body vibration. Part 2: Vibration in buildings (1 Hz to 80 Hz). International Organization for Standardization, Geneva, 2003.

Search CrossRef
ISO 8041 Human response to vibration-Measuring instrumentation. International Organization for Standardization, Geneva, 2005.

Search CrossRef
Grinffin M. J. Handbook of human vibration. London, Academic Press, 1994.

Search CrossRef
Hendron A. J., Oriard L. L. Specifications for controlled blasting in civil engineering projects. Proc. RETC 2, 1972, p. 1585-1609.

Search CrossRef
Wiss J. A., Paramelee R. A. Human perception of transient vibrations. J. Struct. Div.-ASCE, Vol. 100, Issue ST4, 1974, p. 773-787.

Search CrossRef
Siskind D. E., Stagg M. S., Kopp J. W., et al. Structure response and damage produced by ground vibrations from surface blasting. RI 8507, U.S. Bureau of Mines, Washington D.C, 1980.

Search CrossRef
Walter E. J., Walter E. J. Jr. Low level continuous vibration and potential damage. Gen Proc Ann Conf Explosives and Blasting Res ISEE CD-ROM database, 1979.

Search CrossRef
Heggie R. Advanced blasting technology reports, 1978 guide for evaluation of exposure to whole body vibrations. International Standards Organization 2631 Addendum 1, 1988.

Search CrossRef
St. George J. D. Ground vibrations from blasting: the human response. Aus. IMM New Zealand Branch Ann. Conf., Christchurch, 1998, p. 113-120.

Search CrossRef
Cengiz K., Erim G. The problem of human response to blast induced vibrations in tunnel construction and mitigation of vibration effects using cautious blasting in half-face blasting rounds. Tunnel. Underg. Space Technol., Vol. 24, 2009, p. 53-61.

Search CrossRef
Gilbert F. K., Kenneth J. G. Explosive shocks in air. Berlin, Springer-Verlag, 1985.

Search CrossRef
Iyama J., Kuwamura H. Application of wavelets to analysis and simulation of earthquake motions. Earthquake Engng. Struct. Dyn., Vol. 28, Issue 2, 1999, p. 255-272,

Search CrossRef
Osama M., Al-Hunaidi, Guan W. Digital frequency-weighting filters for evaluation of human exposure to building vibration. Noise Control Engineering Journal, Vol. 44, Issue 2, 1996, p. 79-91.

Search CrossRef
Rimell A. N., Mansfield N. J. Design of digital filters for frequency weightings required for risk assessments of workers exposed to vibration. Ind. Health, Vol. 45, 2007, p. 512-519.

Search CrossRef
ISO 10137 Bases for Design of Structures-Serviceability of Buildings and Walkways against Vibrations. International Organization for Standardization, Geneva, 2007.

Search CrossRef

About this article

Received

28 October 2013

Accepted

22 December 2013

Published

31 March 2014

Keywords

blasting operation

vibration

acceleration

comfort

vibration dose

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 51009104).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.