Modal analysis of cable-tower system of twin-span suspension bridge

2.1. Construction details of the twin-span suspension bridge

Ma’anshan Bridge is a bridge over the Yangtze River in Ma’anshan, Anhui, China. It ties with Taizhou Bridge as the longest double span suspension bridge with a span arrangement of 360+2×1080+360 m as shown in Fig. 1.

Fig. 1General layout of Ma’anshan Yangtze River bridge (unit: m)

Two main cables of 35 m apart are made of galvanized high-tensile steel wires with a diameter of 5.2 mm and an ultimate tensile strength of 1670 MPa by prefabricated parallel-wire strands (PPWS). Each main cable consists of 154 strands and each strand weight 49T with 91 wires built into it. The outer diameter is approximately 0.688 m, and, the volume-weight and elasticity modulus of the main cable are 78.5 kN/m³ and 200 kN/mm² respectively.

The double hanger rope is also made of high-tensile galvanized parallel wire bundles. Each hanger is composed of 109 parallel steel wires with a diameter of 5.0 mm and an ultimate tensile strength of 1670 MPa. The spacing between two adjacent hangers is 16.0 m while the separation distance from tower center to the nearest hanger is 20.0 m.

The mid-tower and two side towers are portal-type frames with two cross-beams installed between two tower legs. As Fig. 2 shows, the height of the tower is 178.8 m measured from the top surface of the pile cap to the pylon top. Besides 10.5 m decoration segment part at the top, the 127.8 m steel upper part from the bottom of the saddle downwards of the mid-tower is connected to the 40.5 m lower concrete part by the steel-concrete connection joint segments just beneath the bottom steel cross-beam. The centre-lines of the tower legs are 35 m apart at the top tower increasing to 43.5 m at the pile cap. The width of the leg is constant at 6 m in the tower plane, but in the plane of bridge tapers from 11 m at top steel-concrete joint section to 7 m at the top tower. For the pre-stressed reinforced concrete bottom tower, the widths reduces from 12 m in tower plane and 25 m in the bridge plane at the pile cap to 9.2 m and 17 m at the joint section , and, the corresponding thicknesses are 1.6 m and 2.0 m of the box section respectively, while the joint is a solid block. As for the side towers, the width of the legs are both constant at 6 m in tower plane and at 8 m in the plane of the bridge. Other dimensions are nearly the same as those of the mid-tower.

Fig. 2The principal dimension of mid-tower

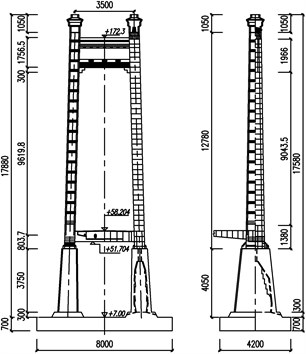
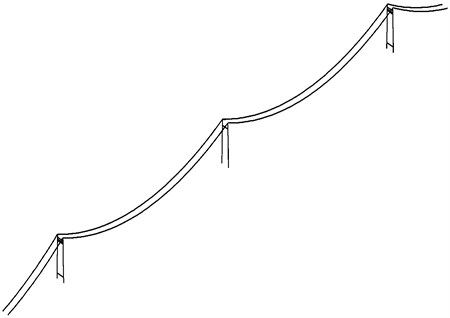
Fig. 3FEM of cable-tower system of twin span suspension bridge

2.2. Finite element modelling

A three-dimensional finite element model is established for Ma’anshan suspension bridge using MIDAS Civil (2012) software. Subsequently, the supports, girders, and the hangers are dismantled following the reverse process of the construction in order to obtain the FE model of the tower-cable system as shown in Fig. 3. In this model, three dimensional Timoshenko beam elements are used to model the thick cross-beams and legs fixed at the base of the tower. The stiffening girders are modeled with beam elements passing through the centroids of the girder sections. The anchor points of the hangers on the stiffening girders are connected to the central beam by imaginary rigid beams. All hangers and main cables are modeled with truss elements with Ernst’s equivalent elastic modulus. The model has 913 nodes and 1177 elements. The modulus of elasticity of the upper mid-tower and side towers are 210 kN/mm² and 34.5 kN/mm² respectively. The Poisson ratio of mid-tower is 0.3 and that of the side towers is 0.2. The volume-weight of the upper mid-tower and the side towers are 76.98 kN/m³ and 25 kN/m³ respectively [13, 16].

The tower-cable system described above is slightly modified with the consideration of the actual construction conditions associated with the completion of the erection process. For instance, the masses of the working cranes, cable saddles and platforms connected to the top of the towers are added to the corresponding nodes as additional lumped masses. The results of the static analysis of the tower-cable system show that the mid-span sag of the main span is 111.663 m which is 8.337 m smaller than that of the post construction state.

Based on this model, an extensive numerical analysis of the modal characteristics of the isolated cable, free standing tower and tower-cable coupling system are carried out and presented in the following sections.

3.1. Isolated main span cable

Due to the symmetry of the structure, only the isolated left main span cable is studied in this section. The first fifteen natural frequencies for in-plane and out-plane vibration of the isolated suspended cable based on Irvine-Caughey method [17] and FEA software respectively are tabulated in Table 1,and the mode shapes are shown in Fig. 4. As the results show, the in-plane and out-of-plane vibration modes are uncoupled. The relative difference of natural frequency between the two methods is less than 3.48 %. As can be observed from Fig. 4, the vertical component of the first in-plane vibration mode of the isolated left main span cable is antisymmetric single wave while the first mode of the out-of-plane vibration is symmetric half-wave, and the first natural frequency of in-plane vibration of the cable is almost twice the first natural frequency of out-of-plane vibration. These results are consistent with Irvine-Caughey free vibration theory [17]. The consistency between the two results above indicates the accuracy of the FE model.

Fig. 4First mode shapes of isolated main span cable

a) The first in-plane mode

b) The first out-of-plane mode

3.2. Isolated side span cable

Similarly, the first ten natural frequencies for in-plane and out-plane vibration of isolated side span cable are tabulated in Table 2, and, the mode shapes are shown in Fig. 5. As can be observed from Fig. 5, the vertical component of the first in-plane vibration mode of isolated left side span cable is antisymmetric single wave, while the first mode of the out-of-plane vibration is symmetric half-wave.

The $i$th natural frequencies of the isolated side span cable are always larger than either in-plane or out-of-plane natural frequencies of the isolated main span cable. The lower natural frequencies of the isolated side span cable are closed to the higher natural frequencies of the isolated main span cable. Therefore, it can be predicted that, in the tower-cable coupling system, some internal resonances exist between the higher vibration modes of the main span cables and the lower vibration modes of the side span cables.

For instance, because the first in-plane natural frequency, 0.3270 Hz, of the isolated side span cable is between the fifth and the sixth in-plane natural frequency of the isolated main span cable, it will excite the vibration of the side span cable during the fifth vibration mode of main span cable and turns that to the sixth vibration mode. However, the first five vibration modes of the main span cable cannot cause free vibration of the side span cable.

Fig. 5First mode shapes of isolated side span cable

a) The first in-plane mode

b) The first out-of-plane mode

3.3. Free-standing towers

Due to the symmetry of the left and the right side tower, only the left side and the middle tower are studied herein. The first nine natural frequencies of the left side tower and the first six natural frequencies of the mid-tower, including the bending mode, torsional mode and sway mode, are listed in Table 3, and, the first bending, torsional and sway modes of the left side tower are shown respectively in Fig. 6.

From Tables 1-3, we can observe that the first sway frequency of the left side tower, 0.2589 Hz, is between the first and the second natural frequency, 0.1513 Hz and 0.3014 Hz, of the out-of-plane vibration of the side span cable, is close to the fifth natural frequency 0.2595 Hz of the out-of-plane vibration of the main span cable. The first sway frequency of mid-tower, 0.6052 Hz, is close to the twelfth natural frequency of the out-of-plane vibration of the main span cable and the fourth natural frequency, 0.5953 Hz, of the out-of-plane vibration of the side span cable. Hence, it can be predicted that the first sway mode of towers appears along with the higher out-of-plane vibration mode of the main span cables in the tower-cable system. Due to the dynamic interaction between the towers and the cables in the coupled system, the in-plane modal properties of the cables and the towers will be changed.

Fig. 6First mode shapes of free-standing left side tower

a) The first bending mode

b) The first sway mode

c) The first torsion mode

4.1. Local in-plane vibration

4.1.1. Local in-plane vibration of cables

The natural frequencies of local in-plane vibration modes for main span cables and side span cables in tower-cable system are listed in Table 4 and Table 5 respectively. Table 4 shows the first thirty-three natural frequencies of vibration modes. The fourth and eighth columns are the abbreviated description for the vibration modes of cables. For the purpose of better clarification two capital letters are defined to describe the modal combination of cables. The first letter stands for the Symmetric mode, with S, and Antisymmetric mode, with A, for any single span. The second explains the relationship between any two spans with A and C to denote Axial-symmetry and Central-symmetry modes about the mid-tower respectively.

Table 4Natural frequencies of local in-plane modes of vibration of main span cables

Mode no.	Natural frequency (Hz)	Modal property	Modal combination	Mode no.	Natural frequency (Hz)	Modal property	Modal combination
1	0.1075	in phase	AA	18	0.4252	out of phase	AC
2	0.1075	out of phase	AA	19	0.5297	in phase	AA
3	0.1075	in phase	AC	20	0.5297	out of phase	AA
4	0.1075	out of phase	AC	21	0.5297	in phase	AC
5	0.1517	out of phase	SA	22	0.5620	in phase	SA
6	0.2138	in phase	AA	23	0.5625	out of phase	SA
7	0.2138	out of phase	AA	24	0.5962	in phase	SA
8	0.2138	in phase	AC	25	0.5966	out of phase	SA
9	0.2138	out of phase	AC	26	0.6330	in phase	AA
10	0.3198	out of phase	AA	27	0.6330	out of phase	AA
11	0.3198	in phase	AA	28	0.6856	in phase	SA
12	0.3199	out of phase	AC	29	0.6861	out of phase	SA
13	0.3199	in phase	AC	30	0.7340	in phase	AA
14	0.3682	in phase	SA	31	0.7354	out of phase	AA
15	0.4252	in phase	AA	32	0.7386	in phase	AA
16	0.4252	out of phase	AA	33	0.7854	in phase	SA
17	0.4252	in phase	AC

Comparing the data of Table 4 with the natural frequencies of isolated main span cables in Table 1, it is evident that Table 4 almost includes all the natural frequencies in Table 1. It indicates that the local in-plane vibration modes of tower-cable system still holds the modal characteristics of each component of tower-cable coupled system, but it also has new unique modal characteristics different from the isolated single cable. For example, all the first four natural frequencies in Table 4 are 0.1075 Hz, and the corresponding mode shapes of single main span cables are still single wave as the Fig. 7 shows. There are four types of modal combination, two of the modes are single span Antisymmetry with double span Axial-symmetry (AA) in-phase mode and out-of-phase mode of vibrations, the other two are single span Antisymmetry with double span Central-symmetry (AC) of in-phase and out-of-phase modes. Thus, the frequencies of tower-cable system in Table 4 can be divided into some groups according to frequencies of isolated cables in Table 1. Such as the first four natural frequencies in Table 4 according to the first in-plane natural frequency 0.1075 Hz in Table 1, the fifth natural frequency in Table 4 according to the second natural frequency 0.1520 Hz in Table 1 and the sixth to ninth natural frequency in Table 4 according to the third natural frequency 0.2138 Hz in Table 1 and so on. Similarly, from Table 5 and Table 1, the natural frequencies of local in-plane vibration of side span cables are divided into groups.

There are several coupling resonances between higher order modes of main span and the modes of side span according to Table 4 and Table 5. For instance, the first local in-plane vibration in which the corresponding natural frequency is 0.3198 Hz of side span cables excites the tenth local in-plane vibration of main span cables. However, as Fig. 8 shows, the fifteenth vibration mode of main span cable is single span Symmetric mode in which the additional tension of cable is zero which means it doesn’t excite the vibration of side span cable, thus, there is no natural frequency in Table 5 that matches that. Similarly, the natural frequency for the third vibration mode of side span cables in Table 1 does not have a corresponding frequency in Table 4.

Table 5Natural frequencies of local in-plane modes of vibration of side span cables

Mode no.	Natural frequency (Hz)	Modal property	Modal combination	Mode no.	Natural frequency (Hz)	Modal property	Modal combination
1	0.3198	out of phase	SA	10	0.5966	out of phase	SA
2	0.3270	out of phase	AC	11	0.6458	in phase	AC
3	0.3271	in phase	AA	12	0.6458	in phase	AA
4	0.3271	in phase	AC	13	0.6856	in phase	SA
5	0.3276	out of phase	AA	14	0.6861	out of phase	SA
6	0.3682	in phase	SA	15	0.7340	in phase	SA
7	0.5620	in phase	SA	16	0.7354	out of phase	SA
8	0.5625	out of phase	SA	17	0.7386	in phase	SA
9	0.5962	in phase	SA	18	0.7854	in phase	SA

It is interesting that, along with the local in-plane vibration, all modal combinations of side span cables are single span Symmetry with double spans Axial-symmetry (SA) in Table 5. It can also be observed from Fig. 7 and Fig. 8 that the towers generate some relatively small motion when the local natural frequencies of cables are close to the local frequencies of towers or the global frequencies of the system.

Fig. 7The first four local in-plane mode shapes of main span cables

a) In phase (AA)

b) Out of phase (AA)

c) In phase (AC)

d) Out of phase (AC)

Fig. 8The local in-plane mode shapes of main span cables and side span cables

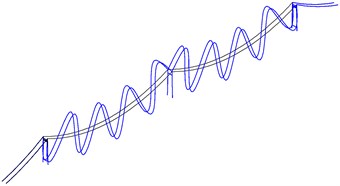
a) The fifteenth modal motion of main span cables

b) The third modal motion of side span cables

4.1.2. Local in-plane vibration of two side towers

The natural frequencies of local in-plane vibration of two side towers of tower-cable system are listed in Table 6. Affected by the main cables in the local in-plane vibration of tower-cable system, some new natural frequencies of bending mode and torsional mode of side tower are generated as compared with Table 3, and, the lower order frequencies are closely spaced. The result also shows that all the modal properties of bending mode and torsional mode of two side towers are out-of-phase in the local in-plane vibration mode of side towers, and, when bending is the dominant mode of two side towers, all the modal properties of two cables are in-phase, while when torsion is the dominant mode of two side towers all the modal properties of two cables are out-of-phase.

Table 6Natural frequencies of local in-plane modes of vibration of two side towers

Mode no.	Bending mode (out of phase)			Torsion mode (out of phase)
	Natural frequency (Hz)	Two cables		Natural frequency (Hz)	Two cables
		Modal property	Modal combination		Modal property	Modal combination
1	0.1465	in phase	SA	0.2595	out of phase	SA
2	0.1767	in phase	SA	0.3207	out of phase	SA
3	0.2631	in phase	SA	0.3693	out of phase	SA
4	0.4626	in phase	SA	0.4654	out of phase	SA
5	0.4814	in phase	SA	0.4900	out of phase	SA

It is interesting that, for either the bending mode or the torsional mode, all the modal combinations of two cables are single span Symmetry with double span Axial-symmetry (SA). The second bending and torsional mode of side towers in local in-plane vibration are shown in Fig. 9. It can be seen that the second bending frequency 0.1767 Hz of side towers excites the second vibration mode of main span cables and the half-wave mode of side span cable. The second torsional frequency 0.3207 Hz of side towers excites the fifth vibration mode of main span cables and the first mode of side span cable. Therefore, it can be concluded that, in the local in-plane vibration of triple-tower twin-span tower-cable system, the larger out of phase bending vibration mode of two side towers will excite the main cable as an in-phase modal combination which is single span Symmetry with double span Axial-symmetry (SA). While the larger out of phase torsional vibration of the side towers will excite a similar modal combination but out-of-phase.

Fig. 9The second local in-plane mode shapes of two side towers

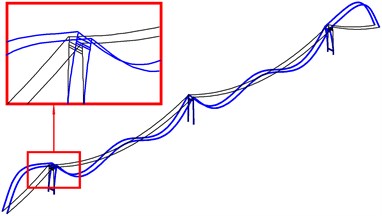
a) The second bending mode (in phase) (SA)

b) The second torsional mode (out of phase) (SA)

4.1.3. Local in-plane vibration of mid-tower

Table 7 lists the natural frequencies of local in-plane vibration modes for the mid-tower. Similarly, compared with table 3, some new natural frequencies of bending mode and torsional mode of side tower are generated and are closely spaced. In the local in-plane vibration modes of mid-tower, for the bending mode of mid-tower all the modal properties of two cables are in-phase, while for the torsional mode of mid-tower the modal properties of two cables are out-of-phase.

It is obvious that either for the bending modes or the torsional modes, all the modal combinations of two cables are single span Symmetry with double span Central-symmetry (SC) and the side span cables have no motion or only slight motion. Fig. 10 shows the first bending and torsional mode of the local in-plane vibration mode of mid-tower. The first bending frequency 0.3735 Hz excites the sixth vibration mode of main span cables, and, the first torsional frequency 0.1499 Hz excites the second vibration mode of main span cables while the side span cables experience almost no motion at all. Hence, it can be concluded that, in the local in-plane vibration of three-tower and two-span tower-cable system, the larger bending vibration mode of mid-tower will excite an in-phase modal combination which is single span Symmetry with double span Central-symmetry (SC) of main cables. While the larger torsional vibration will excite a similar modal combination but out-of-phase mode of the main cable.

Table 7Natural frequencies of local in-plane modes of vibration of mid-tower

Mode no.	Bending mode			Torsion mode
	Natural frequency (Hz)	Two cables		Natural frequency (Hz)	Two cables
		Modal property	Modal combination		Modal property	Modal combination
1	0.3735	in phase	SC	0.1499	out of phase	SC
2	0.4777	in phase	SC	0.5820	out of phase	SC
3	0.5813	in phase	SC	0.6838	out of phase	SC

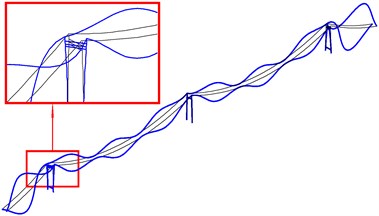
Fig. 10The first local in-plane mode shapes of mid-tower

a) The first bending mode (in phase) (SC)

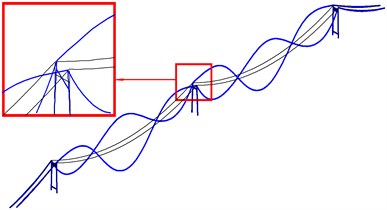
b) The first torsional mode (out of phase) (SC)

4.2. Global in-plane vibration

The natural frequencies of global in-plane vibrations are listed in Table 8. It is still clear that the lower order natural frequencies present are closely spaced. Both the bending and torsional modes of two side towers are in phase. For the bending mode the modes of cable are in phase while for torsional mode of the side tower the modes of cable are out of phase. All the modal combinations of the twin cables are single span Symmetry with double span Central-symmetry (SC). In contrast to the local in-plane vibration mode of mid-tower, the vibration of side span cables are excited in the global in-plane vibration of system due to the vibration of side towers.

The first bending and torsional mode of global in-plane vibration are shown in Fig. 11. The first bending frequency of the tower-cable system 0.1297 Hz is a new outcome just between the first and the second natural frequency of isolated main span cable, and, smaller than the first natural frequency of isolated side span cable. The fourth vibration mode of main span cables and the half-wave mode of side span cables are excited by the first torsional frequency, 0.2497 Hz, close to the fourth natural frequency of isolated main span cable. Fig. 12 shows the second bending and torsional mode of global in-plane vibration respectively. Similarly, the second vibration mode shape of main span cables and the half-wave mode shape of side span cables are excited by the second bending frequency of 0.1696 Hz. While the second torsional vibration mode excites the fifth vibration mode of the main span cables and the similar mode of the side span cables. The new frequency of the tower-cable system is the result of coupling effect of the components with each other. From Table 8, it can be observed that in global in-plane vibration of twin-span tower-cable system, large bending or torsional mode with two side towers in phase, will excite the vibrations in phase mode of two cables with the single span Symmetry and with double spans Central-symmetry (SC). As the torsional mode of the side tower is concerned, the same SC modes are excited but out of phase only. That is much more relevant to the local in-plane vibration of towers.

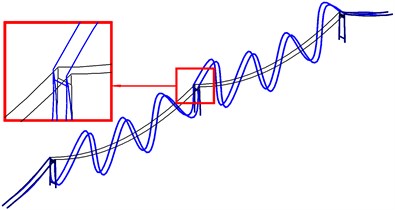
Fig. 11The first bending mode and torsion mode of global in-plane vibration of cable-tower system

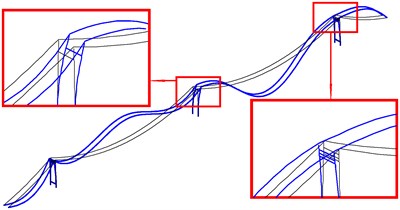
a) In phase (SC)

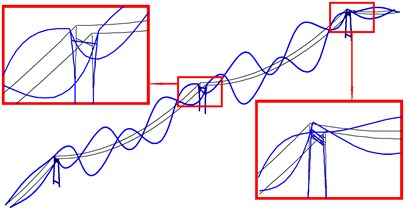
b) Out of phase (SC)

Fig. 12The second bending mode and torsion mode of global in-plane vibration of cable-tower system

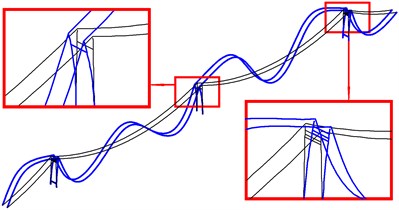
a) In phase (SC)

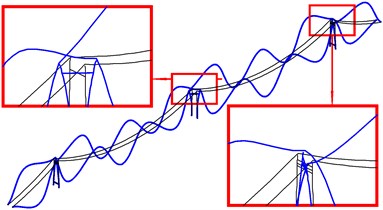
b) Out of phase (SC)

4.3. Local out-of-plane vibration

Similar to the in-plane vibration, the out-of-plane vibration of three-tower and two-span tower-cable system is divided into the local and global out-of-plane vibration. The local out-of-plane vibration is subdivided into the local out-of-plane vibration of cables, side towers and the mid-tower.

4.4. Global out-of-plane vibration

Table 13 lists the natural frequencies of global out-of-plane vibration of the tower-cable system. It is interesting that the sway natural frequencies of the system are just between the first sway natural frequency of the side tower and the mid-tower. The modes of two cables are in phase Axial-symmetry modes. Thus, the sway modal properties of two side towers must be in phase and the corresponding natural frequencies always excite the out-of-plane vibration of the mid-tower. Subsequently, with the interactions between three towers and two cables, the sway natural frequencies of two side towers and the mid-tower tend to couple. This results in increasing the sway natural frequencies of the side towers and decreases the sway natural frequencies of the mid-tower.

From the above modal analysis, we conclude that the in-plane and out-of-plane dynamic response of the tower-cable system to wind excitation should be computed using the coupled system model rather than the separate free-standing tower model and isolated model. As the interaction relationship between the towers and the main cables indicate, the natural frequencies of the tower-cable system are more closely spaced and are lower than those of the free-standing towers. The cross-correlation terms and the higher modes may have to be taken into account as the wind response is considered.

The modes of the cable-tower system are categorized and described in details, and important issues such as modal combination problems have been elaborated. However, for the initial curvature and stretching parameters of the cables being neglected, the nonlinearity effects due to quadratic and cubic items were not introduced into the cable-tower dynamic system above. It is speculated and possibly expected that more nonlinear characteristics such as internal resonance or mode bifurcation may develop when certain conditions such as yielding the inner resonance is satisfied, for the twin-span suspension bridge with large span is always a flexible structure especially in the construction period. The complex nonlinear modal effects will be subject of further research by the authors.