Concrete creep and thermal effects on the dynamic behavior of a concrete-filled steel tube arch bridge

Zhou, Yao

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2014

Check for updates

Concrete creep and thermal effects on the dynamic behavior of a concrete-filled steel tube arch bridge

Yao Zhou¹

¹School of Transportation Science and Engineering, Beihang University, Beijing, 100191, China

Cite the article Download PDF

Downloads 1224

Abstract

A solution to the dynamic problem of concrete-filled steel tube arch bridge including concrete creep and thermal effects are presented. Using a new method to calculate the creep of axially compressed concrete-filled steel tube members, the predicted values of the stress and deformation of the Yajisha Bridge in China are consistent with the site measured data. Using the elastic continuation and plastic flow theory and the unified theory of concrete-filled steel tube columns, the dynamic responses of the Yajisha Bridge are analyzed. The influence of creep effects is more significant, especially in the early aging of concrete. It is found that temperature deteriorates the modulus of elasticity of concrete significantly. Consequently the natural frequencies decrease with temperature increase. Concrete creep and thermal effects are essential to evaluate dynamic behavior of concrete-filled steel tube arch bridge.

1. Introduction

Steel members have the advantages of high tensile strength and ductility, whereas concrete members have the advantages of high compressive strength and stiffness. Composite members combine steel and concrete, resulting in a member that has the beneficial qualities of both materials. Using concrete-filled steel tubes (CFSTs) for the arch ribs of an arch bridge is tenable because CFSTs are resistant to axial compressive forces. The steel tube also acts as a formwork for the concrete during construction of the bridge, thus saving a major construction cost. Because of these advantages, it is possible to reduce the cost of constructing bridges. More than 100 CFST arch bridges have been constructed in China since the 1990’s. The seismic properties of CFST arch bridges have been the subjects of recent research. The seismic properties of a partially CFST arch bridge in China have been previously discussed, and the effect of the filled concrete length of steel tube on the nonlinear seismic responses of an arch bridge was examined [1]. An analysis of the traveling wave effect on the seismic response of a CFST arch bridge and the seismic response of an arch bridge with irregular CFSTs were also conducted [2-3]. However, only a small number of studies on the effects of creep on the dynamic properties of a CFST arch bridge have been conducted. Creep is the development of additional strains in a material over time. Current studies on concrete creep focus on the composition of the concrete materials and the creep effects on the structural static properties, rarely considering the effects on the structural dynamic properties.

Li studied the dynamic responses of a high-speed railway bridge subjected to moving trains and considered the effects of temperature and creep. These results indicated that the deck deformation considering creep effects, after eliminating the deformation under static load, is larger than that when not considering creep [4]. A solution to the dynamic problem of reinforced concrete slab-and-beam structures including creep and shrinkage effects was presented by Sapountzakis E. J. and Katsikadelis J. T. [5]. The evaluated eigenfrequencies decreased with time due to the predominant action of creep compared to shrinkage. When the creep occurred at 1000 days, the maximum values of the dynamic deflections at the center and at the middle of the free side of the plate are 2.05 times and 2.07 times that without the influence of creep, respectively.

Temperature changes are known to affect the dynamic properties of bridges significantly so that much experimental research in this area has been conducted. Researchers find that the first three natural frequencies of the Alamosa Canyon Bridge varied about 4.7 %, 6.6 % and 5.0 % during a 24 h period as the temperature of the bridge deck changed by approximately 22°C [6]. The Z24 Bridge in Switzerland is continuously monitored for nearly a year. The first four vibration frequencies vary by 14 %-18 % during the 10 months [7]. A study of the concrete creep and thermal effects on the seismic properties of a CFST arch bridge is presented in this paper.

2. Fundamental theory of concrete creep

The creep of concrete has been studied extensively, and there are many theories and methods such as effective modulus method (EMM), age-adjusted effective modulus method (AEMM), elastic continuation and plastic flow (ECPF) theory to analyze this phenomenon [8-9].

2.1. Creep model

Based on the ECPF theory, concrete creep consists of recovered creep and the unrecovered creep. The compliance function of concrete creep can be decomposed as [10]:

1

J (t, t_{0}) = \frac{1}{E (t_{0})} + C_{d} (t - t_{0}) + C_{f} (t, t_{0}),

where $t_{0}$ is the concrete age of initial loading; $E (t_{0})$ is modulus of concrete at age $t_{0}$ ; $t$ is the age of concrete after casting; $C_{d} (t - t_{0})$ is the sluggish recovered creep under unit stress; and $C_{f} (t, t_{0})$ is the unrecovered creep under unit stress.

The creep calculation formula, based on the ECPF theory, is expressed as follows:

2

ε (t) = \frac{σ (t)}{E (t)} + \int_{t_{0}}^{t} σ (t) ξ (t, τ, t_{0}) d τ,

where $σ (t)$ is concrete stress at age $t$ :

3

ξ (t, τ, t_{0}) = ξ_{d} (t, t_{0}) + ξ_{f} (t, t_{0}),

4

ξ_{d} (t, t_{0}) = - \frac{\partial}{\partial τ} C_{d} (t - τ),

5

ξ_{f} (t, t_{0}) = \frac{d}{d τ} C_{f} (τ, t_{0}) - \frac{d}{d τ} \frac{1}{E (τ)} .

Expand the kernel $ξ (t, τ, t_{0})$ and $ξ (t, τ, t_{0})$ of the ECPF theory as a Dirac series, and then integrate the series to determine $J (t, t_{0})$ :

6

C_{d} (t - t_{0}) = \sum_{i = 1}^{2} c_{i} (1 - e^{- γ_{i} (t - t_{0})}),

C_{f} (t, t_{0}) = \sum_{j = 3}^{4} c_{j} (1 - e^{- γ_{j} (t - τ)}) .

According to the experimental data, $γ_{1} = 2.7 d^{- 1},$ $γ_{2} = 0.14 d^{- 1},$ $γ_{3} = 1.15 d^{- 1},$ $γ_{4} = 0.015 d^{- 1},$ $c_{1} = 1.51×10 -6 mm 2 /N,$ $c_{2} = 3.24×10 -6 mm 2 /N,$ $c_{3} = 2.17×10 -6 mm 2 /N,$ $c_{4} =$ 8.85×10^-6 mm²/N.

2.2. Creep analysis of axially compressed CFST members

A redistribution of stress on the cross-section occurs during the creep process, and the formula to calculate the changed force on members is expressed as:

7

N_{c}^{c} + N_{s}^{c} = 0,

where $N_{c}^{c}$ is the increment of internal force of the core concrete; and $N_{s}^{c}$ is the increment of internal force of the steel tube.

In Fig. 1, $ε_{c}^{c}$ is the increment of the free creep of the core concrete; $ε_{s}^{c}$ is the increment of strain of the steel tube after creep; $ε_{c}^{c 1}$ is the resile strain of the core concrete under the confining stress of the steel tube axially compressed CFST members.

Fig. 1Deformation pattern of CFST creep

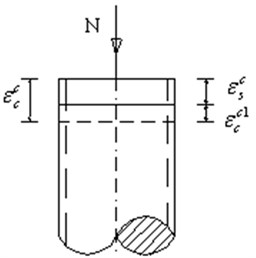
When creep of CFST members occurs, Eq. (7) can be written as:

8

σ_{c}^{c} A_{c} + σ_{s}^{c} A_{s} = 0,

where $σ_{c}^{c}$ is the increment of the stress of core concrete after creep; $σ_{s}^{c}$ is the increment of stress of the steel tube after creep; $A_{c}$ is the area of the core concrete; and $A_{s}$ is the area of the steel tube.

After creep occurs, the strain increment of the steel tube is:

9

ε_{s}^{c} = \frac{σ_{s}^{c}}{E_{s}},

where $E_{s}$ is the modulus of elasticity of the steel tube. $ε_{s}^{c}$ is changed by $σ_{s}^{c}$ after the steel tube experiences a stress redistributions; Du Jinsheng believes that the creep strain of a steel tube was thus equal to the creep strain increment of the CFST, $ε_{s c}^{c}$ . Consequently:

10

ε_{s c}^{c} = ε_{s}^{c} .

The stress of the core concrete is:

11

σ_{c} = σ_{0} + σ_{c}^{c},

where $σ_{0}$ is the initial axial stress of the core concrete.

According to Eq. (8):

12

σ_{s}^{c} = - \frac{σ_{c}^{c}}{α},

where $α$ is the steel ratio of CFST members and $α = A_{s} / A_{c}$ .

By combining Eq. (9) with Eq. (12):

13

σ_{c}^{c} = - α E_{s} ε_{s}^{c} .

According to the relation between stresses in the steel tube and in the core concrete, the creep of the core concrete is:

14

ε_{s}^{c} = (σ_{0} + σ_{c}^{c}) J (t, t_{0}) .

By combining Eq. (13) with Eq. (14):

15

ε_{s}^{c} = (σ_{0} - α E_{s} ε_{s}^{c}) J (t, t_{0}),

then:

16

ε_{s c}^{c} = \frac{σ_{0} J (t, t_{0})}{[1 + α E_{s} J (t, t_{0})]} .

By combining Eq. (11) and Eq. (14) with Eq. (16), the stress in the core concrete is as follows:

17

σ_{c} = \frac{σ_{0}}{[1 + α E_{s} J (t, t_{0})]} .

In accordance with the above formula, the creep of the axially compressed CFST members, i.e., $ε^{t}$ can be expressed as:

18

ε^{t} = ε_{0} + ε_{s c}^{c},

where $ε_{0}$ is the initial strain of the CFST.

Because the force of the arch rib is small, and the creep of the CFST member is smaller than the creep of the concrete under the identical conditions. Thus, to simplify the calculations, the elastic material behavior of creep with time is assumed to be linear and the reduced modulus of elasticity of composite, $E_{s c}^{t}$ , is given as:

19

E_{s c}^{t} = \frac{N}{ε^{t} A_{s c}},

where $A_{s c}$ is the area of CFST, $A_{s c} = A_{s} + A_{c}$ ; and $N$ is the axial force on the CFST members.

3. Unified theory of CFST

Considering the CFST member as a single material, the material modulus of elasticity is given as [11]:

20

E_{s c} = \frac{f_{s c}^{p}}{ε_{s c}^{p}},

f_{s c}^{p} = (\frac{0.172 f_{y}}{235} + 0.488) f_{s c}^{y},

ε_{s c}^{p} = \frac{0.67 f_{y}}{E_{s}},

where $f_{s c}^{p} = (1.213 ζ + B ζ + C ζ^{2}) f_{c k}$ , $ζ = A_{s} f_{y} / A_{c} f_{c k}$ .

For the short circular column of axially compressed CFST members:

B = 0.1759 (\frac{f_{y}}{235}) + 0.974,

C = - 0.1038 (f_{c k} / 20) + 0.0309,

where $f_{y}$ is the yield point of the steel tube; and $f_{c k}$ is the concrete strength standard.

4. Thermal effects on structure

Temperature change affects a structure in a complicated way. It not only affects mechanical properties, but also geometry. Xia assumes that the variation of Young’s modulus and thermal expansion with temperature is linear for small changes in temperature [12]. For a simple-supported beam, the change of vibration frequency $δ f$ is expressed as:

21

\frac{δ f}{f} = \frac{(θ_{T} + θ_{E}) δ T}{2},

where $θ_{T}$ is thermal coefficient of linear expansion of the material; and $θ_{E}$ is the temperature coefficient of modulus. For concrete, $θ_{T} =$ 1.0×10^-5/°C, $θ_{E} =$ –4.5×10^-3/°C; for steel, $θ_{T} =$ 1.0×10^-5/°C, $θ_{E} =$ –3.6×10^-4/°C. Therefore, the variation of Young’s modulus with temperature is much more significant than thermal expansion.

5. Creep effects analysis of a CFST arch bridge

5.1. Structural model of the Yajisha CFST arch bridge

The main bridge of the Yajisha is a half-through and non-hinged arch bridge with a main span of 344 m [13]. The arch ribs are designed in the shape of a catenary with an arch rise of 76.45 m and a ratio of rise to span of 1/4.5. Each arch rib is constructed of six CFSTs, which are made of Ø750 steel tube, and are connected into a CFST truss with transverse flat plates connecting web members. The size of outer and inner steel tubes of the truss is Ø750 mm×18 mm, the size of middle steel tube is Ø750 mm×20 mm, and the thickness of transverse flat plates between the steel tubes is 500 mm. C50 concrete is filled into the tubes of arch ribs and transverse flat plates. The structural model of the Yajisha CFST arch bridge is shown in Fig. 2.

Fig. 2Structural model of the Yajisha CFST arch bridge

5.2. Creep effects on the static analysis of arch bridge

Fig. 3 and Fig. 4 illustrate the stress curves of the concrete and steel tube at the middle span of the arch bridge. The stress of the steel tube at the middle span of the arch bridge increases as the creep develops; however, the stress of the concrete at the middle span decreases. The deflection of the CFST arch ribs initially changes significantly, but the curve develops slowly and is close to horizontal after 180 days. After 540 days, the curve almost reaches zero.

Fig. 3Stress curve of concrete at middle span of the arch bridge

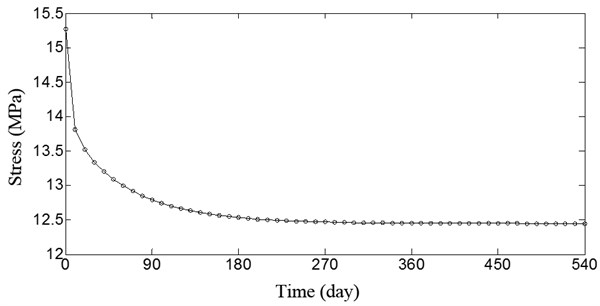
Fig. 4Stress curve of steel tube at middle span of the arch bridge

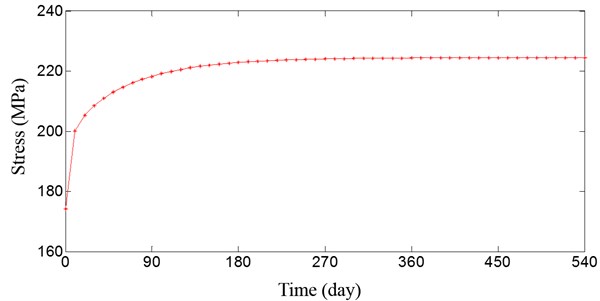
Table 1 illustrates that the first eight computed eigenfrequencies are consistent with those obtained from the model developed by Liu C. W. and Xu S. Q. [13]. The total deflection and stress of the cross-section of the vault of the main arch were measured when the bridge was completed and again after it had been open to traffic for one year [14]. The experimental data and the results calculated using the method of this paper are listed in Table 2. The calculated results for the initial stress of the Yajisha CFST arch bridge, the stress of the vault section after the bridge was completed, the stress of vault section when the bridge open to traffic after one year and the creep of the vault after 540 days are all approximately equal to the experimental data. This indicates that the structural model of the Yajisha CFST arch bridge and the method of calculating CFST creep are accurate.

Table 1Eigenfrequencies of the bridge compared with the other model

Eigenfrequency	Frequency / Hz (Reference Liu and Xu 2000)	Frequency / Hz (This paper)	Aberration (%)
1	0.288	0.288	0.00
2	0.383	0.385	0.50
3	0.539	0.515	4.45
4	0.552	0.537	2.72
5	0.631	0.658	4.28
6	0.688	0.688	0.00
7	0.697	0.762	9.33
8	0.786	0.830	5.60

Table 2Comparison between calculated results and monitoring results

		Measured value	Calculated value
The initial stress of Yajisha CFST arch bridge	The steel tube (MPa)	171	174.1
The initial stress of Yajisha CFST arch bridge	The concrete (MPa)	15.0	15.3
The stress of vault section after the bridge completed	The steel tube (MPa)	206.4	222.8
The stress of vault section after the bridge completed	The concrete (MPa)	13.8	12.5
The stress of vault section when the bridge open to traffic after 1 year	The steel tube (MPa)	218.3	224.4
	The concrete (MPa)	11.3	12.4
The creep of vault after 540 days (mm)		120	115

5.3. Creep effects on the seismic analysis of arch bridge

Fig. 5 shows the natural vibration frequencies become smaller with the age of loading. The rate of frequency change continues to decline and the frequency change occurred mainly in the early stage of creep. The first three frequencies decrease by 8.6 %, 12.8 % and 8.5 % after 540 days, respectively.

Fig. 5Time-dependent change in eigenfrequencies of the arch bridge

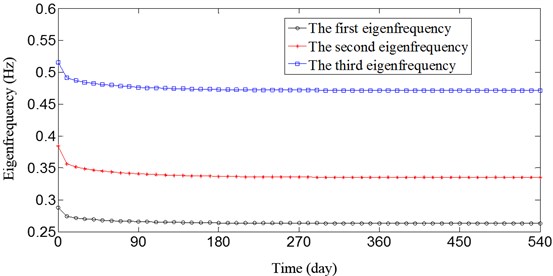
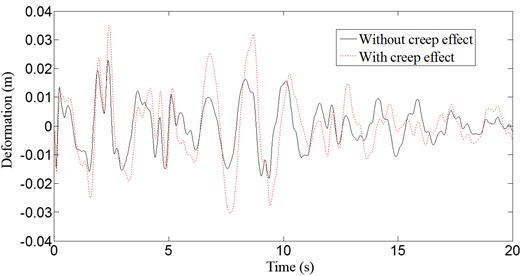
Fig. 6 and Fig. 7 show the displacement response without and with creep at the vault and 1/4 span under the action of vertical earthquake. The seismic wave analyzed in this paper is the El-Centro wave, with an earthquake intensity of 7.75 and a peak of acceleration of 0.15 g. The deflections of the vault and 1/4 span increase 38 % and 53 %, respectively, after creep during an earthquake. The effects of creep on the dynamic analysis of the CFST arch bridge are significant and must be considered. The effects after creep are different depending on location.

Fig. 6Deflection curves at middle span of the arch bridge

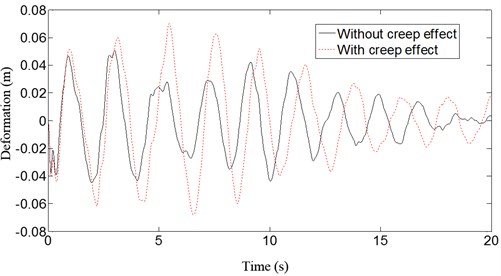
Fig. 7Deflection curves at 1/4 span of the arch bridge

5.4. Thermal effects on the seismic analysis of arch bridge

Fig. 8 and Fig. 9 show the displacement response without and with thermal effects at the vault and 1/4 span under the action of vertical earthquake. The deflections of the vault and 1/4 span increase both 21 % after temperature increases 20°C during the earthquake. Fig. 10 and Fig. 11 show the displacement response without and with concrete creep and thermal effects at the vault and 1/4 span under the action of vertical earthquake. The deflections of vault and 1/4 span increase 46 % and 59 %, respectively, with creep and temperature change. Dynamic behavior of the structure is significantly affected by creep and temperature change, and creep effects are more distinct than thermal effects.

Fig. 8Deflection curves at middle span of the arch bridge

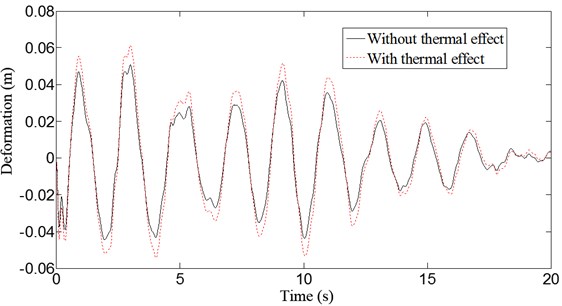
Fig. 9Deflection curves at middle span of the arch bridge

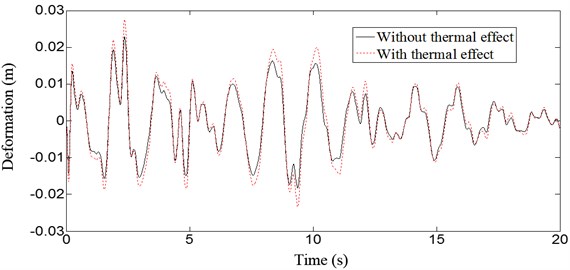
Fig. 10Deflection curves at middle span of the arch bridge

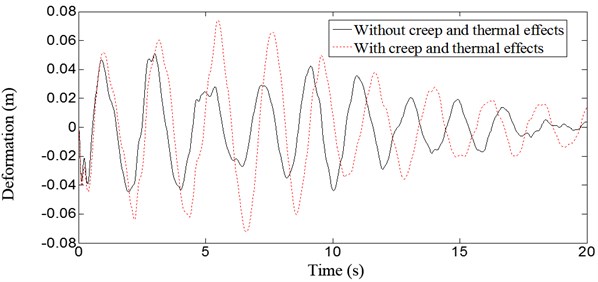
Fig. 11Deflection curves at middle span of the arch bridge

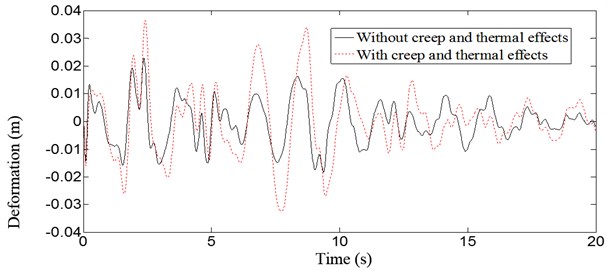
6. Conclusions

The static and dynamic analyses, including creep and thermal effects, of a CFST arch bridge, have been conducted. A realistic model has been adopted and is verified through site tested data. The primary conclusions that can be drawn from this investigation are as follows:

1) In this paper, a structural model of the Yajisha CFST arch bridge simulates the actual characteristics of dynamic response and creep. The mode is convenient to calculate creep effects in the dynamic analysis of the CFST arch bridge.

2) The stress and deformation curves of a CFST arch bridge, influenced by creep, develop quickly initially, and slowly later. The curves trend is nearly horizontal after 180 days and almost reaches zero after 540 days.

3) The stress of the steel tube increases, but the stress of core concrete decreases with creep. The earthquake responses of the 1/4 span of the CFST arch bridge was larger than the earthquake response of the vault. The 1/4 span of the CFST arch bridge needs to be strengthened to prevent the rupture or catastrophic breakdown of the structure under the action of earthquake.

4) The eigenfrequencies decrease with the age of CFST at loading, especially the influence of creep action is more significant in the early age of the arch bridge.

5) The deflections of the CFST arch bridge increase with temperature increase during the earthquake. Concrete creep and thermal effects on the dynamic analysis of the CFST arch bridge are significant and it must be considered.

References

Wu Q. Study on dynamic properties of partially concrete-filled steel tubular arch bridge. Journal of Constructional Steel, Vol. 10, 2002, p. 141-148, (in Japanese).

Search CrossRef
Hu Z. M., Li J. Y., Huang T. Y. Seismic response analysis of concrete-filled steel tube arch bridge based on traveling wave effect. Bridge Construction, Issue 1, 2010, p. 25-28, (in Chinese).

Search CrossRef
Li Y., Yan W. M., Chen Y. J. Seismic response analysis of an arch bridge with irregular concrete-filled steel tube. Technology for Earthquake Disaster Prevention, Issue 3, 2010, p. 346-35, (in Chinese).

Search CrossRef
Li W. Q., Zhu Y., Li X. Z. Dynamic response of bridges to moving trains: a study on effects of concrete creep and temperature deformation. Applied Mechanics and Materials, Vol. 193-194, 2012, p. 1179-1182.

Search CrossRef
Sapountzakis E. J., Katsikadelis J. T. Creep and shrinkage effect on the dynamic analysis of reinforced concrete slab-and-beam structures. Journal of Sound and Vibration, Vol. 260, Issue 3, 2003, p. 403-416.

Search CrossRef
Sohn H., Dzwonczyk M., Straser E. G., et al. An experimental study of temperature effect on modal parameters of the Alamosa Canyon bridge. Earthquake Engineering and Structural Dynamics, Vol. 28, Issue 8, 1999, p. 879-897.

Search CrossRef
Peeters B., De Roeck G. One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthquake Engineering and Structural Dynamics, Vol. 30, 2001, p. 149-171.

Search CrossRef
Naguib W., Mirmiran A. Creep modeling for concrete-filled steel tubes. Journal of Constructional Steel Research, Vol. 59, 2003, p. 1327-1344.

Search CrossRef
Bazant Z. P. Prediction of concrete creep effects using age-adjusted effective modulus method. Journal of the American Concrete Institute, Vol. 69, 1972, p. 212-217.

Search CrossRef
Du J. S. Analysis of Creep influence to concrete-filled steel tubular arch bridges. MS dissertation, Beijing Jiaotong University, Beijing, 2004, (in Chinese).

Search CrossRef
Kuranovas A., Goode D., Kvedaras A. K., et al. Load-bearing capacity of concrete-filled steel columns. Journal of Civil Engineering and Management, Vol. 15, Issue 1, 2009, p. 21-23.

Search CrossRef
Xia Y. Hao H., Zanardo G., et al. Long term vibration monitoring of an RC slab: Temperature and humidity effect. Engineering Structures, Vol. 28, Issue 3, 2006, p. 441-452.

Search CrossRef
Liu C. W., Xu S. Q. Earthquake response of main bridge of Yajisha. Railway Standard Design, Vol. 30, Issue 12, 2000, p. 8-11, (in Chinese).

Search CrossRef
Xin B., Xu S. Q. Creep analysis of a long-span concrete-filled steel tubular arch bridge. Railway Standard Design, Issue 4, 2003, p. 31-33, (in Chinese).

Search CrossRef

About this article

Received

11 March 2014

Accepted

26 May 2014

Published

30 June 2014

Keywords

concrete creep

concrete-filled steel tube

arch bridge

thermal effect

dynamic analysis

Acknowledgements

This research was financially supported by the National Natural Science Foundation of China under Grant No. 51008011 and the China Scholarship Council under Grant No. 201206025022.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.