A fast topology optimization method of damping material layer for noise reduction to elastic curved plate-cavity structure

1. Introduction

In the field of aeronautical, vehicle, naval engineering and the like, many structures may be simplified to elastic plate, curved plate or shell-cavity structure. Dynamic vibration absorber and damping materials are applied widely in vehicle vibration control systems. Damping and topological optimization has been deeply studied [1-8]. Some studies focus on continuum topology optimization methods [9], the Solid Isotropic Material with Penalization (SIMP) method [10-12], the level set method [13-14], Evolutionary Structural Optimization Method [15], maximizing natural frequencies [16-19] or band gaps [20], Direct MultiSearch method [21], optimization problem for minimizing dynamic responses [22-23] or acoustic radiation [24, 25]. However these methods need larger amount of calculation, and are suitable only for simple structures.

Nowadays, studies have been devoted to the optimization of structural-acoustical properties of vibrating structures [26, 27]. Various acoustic characteristics have been taken as target, such as sound power [28, 29], the sound pressure level at a given location [30] and so on. The studies on topology optimization of acoustical properties have been mainly devoted to the optimal distribution of stiffness and mass properties, while the damping layers layout optimization has been rarely addressed.

This paper presents a fast topology optimization formulation and numerical techniques of damping material layer were designed for sound reduction to a curved plate-cavity structure (as schematically illustrated in Fig. 4).

For weight limit reason, damping material could not be pasted on all surfaces. Optimization principle is using less as far as possible the damping materials to reach more effective vibration or noise reduction. The computational model is based on a finite element discretization. Assuming pasting a small amount of damping material on the structural has little effect on vibration mode, the relationship between energy loss of the damping materials on each element and the displacement of each node of the plate (shell) is deduced in a vibration cycle. Principle of the topology optimization method is to paste damping materials on the more effective location, where the element energy will lose most and then the second gradually, until the noise reduction target was achieved. Usually, only one or several modal orders of the structure affect the noise or vibration most. Aimed at the appointed order, only one or several eigenvalues need to be calculated. It is unnecessary to solve a large complex differential equation or matrix eigenvalue. So it is considered as a kind of fast and approximate topology optimization method.

2. Vibration analysis of curved plate or shell structure

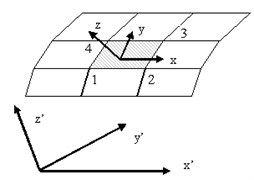
Middle plane of the shell is a curved surface (thin shell diagram and global coordinates and local coordinates of rectangular element are shown as Fig. 1). The displacement in the middle plane and the displacement perpendicular to the surface generally occur simultaneously. Bending state and membrane state are mutual coupling. Generally, there are two kinds of methods to analyze thin shell: one is to use plane element combining folded plate system to replace shell, which combined plane stress and bending stress together to replace the stress of the thin shell; the other is to adopt curved shell element or curved thick shell element directly. In theory, adopting the surface shell element can reflect the real shape of the shell, and obtain accurate results. For most of the mechanical structures are space plate structure or plate-beam combination structure, in this paper plane element was combined to a folded plate system to replace shell and its coordinates which is shown as Fig. 1. Plane stress and bending stress together are used to replace the stress of the thin shell. Element stiffness matrix of the shell is also the stiffness matrix combination of the two kinds of elements.

Fig. 1Sketch of the shell, global coordinates and local coordinates of rectangular element

In the four node quadrilateral plane element, for example, plane stress state has the following relation:

where superscript $m$ means plane stress. $N_i^{\left(m\right)}$ represents shape function of the plane stress model:

where $\xi =2x/l_1$, $\eta =2y/l_2$, which is dimensionless local coordinates. Length and width of the rectangle element are $2l_1$, $2l_2$ respectively. Plate bending state has the following formula:

where superscript $b$ means bending stress. $N_i^{\left(b\right)}$ represents shape function of kirchhoff bending plate element. Let ${\stackrel{-}{X}}_1=1-\xi$, ${\stackrel{-}{X}}_2=1+\xi$, ${\stackrel{-}{Y}}_1=1-\eta$, ${\stackrel{-}{Y}}_2=1+\eta$, we get:

Combining plane stress and bending stress together. Put ${\theta }_{zi}$ into node displacements vector. For local coordinate system, we get:

And in global coordinate system, node displacement vector is:

3. Energy analysis for free damping layer attached to curved plate or shell structure

Damping materials and base metal materials consolidated together. Suppose each layer of the structure is uniform. In the process of vibration, energy dissipation of each layer in one vibration period is equal to the loss factor of layer multiplying the maximum elastic deformation energy. For elastic plate:

Superscript ($m$), ($b$) indicate membrane and bending state respectively, which is:

Shell strain can be decomposed into two parts, which are membrane strain and bending strain respectively. So the deformation of thin shell could also be divided into two parts: membrane strain energy and bending strain energy respectively. Strain energy of the shell can be expressed as:

It is assumed that the strain of the free damping shell at time $t$ is $\sigma \left(t\right)$. Within $dt$, the increment of the strain is $\left\{\dot{\epsilon }\right(t\left)\right\}dt$, and the increment of the strain energy is $d{W}_d={\left\{\sigma \right(t\left)\right\}}^T\left\{\dot{\epsilon }\right(t\left)\right\}\text{d}t$. The strain energy per unit volume at time $t$ is $W_d={\int }_0^t{\left\{\sigma \right(t\left)\right\}}^T\left\{\dot{\epsilon }\right(t\left)\right\}dt$, and the whole energy could be $W={\int }_V{W}_{d}dv$. For the shell is composed of damping material and metal material, the integral area should be these two parts. Then:

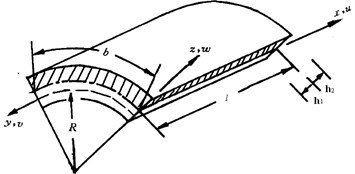
where $V_1$ means volume of metal plate, and $V_2$ means volume of damping material. Sketch of the shell with damping material is shown as Fig. 2.

When strain of the structure changed periodically, we get $\epsilon \left(t\right)={\epsilon }_0\mathrm{c}\mathrm{o}\mathrm{s}\omega t$. Suppose that the base layer is composed of isotropic metal materials. Young’s modulus is $Y_1$, while Poisson’s ratio is $v_1$, and the density is ${\rho }_1$. The variation of the strain energy per unit volume in a cycle is:

The Eq. (11) above describes that the base layer, the metal plate do not experience energy decaying, and energy is unchanged. Constitutive relation of the free damping layer can be described as:

Using three parameters’ viscoelasticity solid modal, relaxation modulus is:

where, $Y\left(0\right)=q_1/p_1$. Set integrating range is $[0,2\pi /\omega ]$ and set $a=(q_1/p_1-q_0)/1+{\omega }^2{p}_1^2$. Under periodical strain effect, $W_{d2}\left(T\right)$ can be calculated as:

The first part of the above Eq. (14) equals zero, which is corresponding to elastic vibration energy per cycle. The latter two integrals represent energy attenuation in a cycle, and the integral range is [0, $t$]. We get:

Solve the above Eq. (15):

When the time is long enough, the value of the second part of the Eq. (16) will verge to a constant $-{\left\{{\epsilon }_0\right\}}^T\left[D_2\right]\left\{{\epsilon }_0\right\}a\omega p_1^2/(1+{\omega }^2{p}_1^2)$. In a vibration steady state, the energy corresponding to the second part of the Eq. (16) attenuate close to zero. So it can be concluded that in steady state vibration, only second integral item needs to be considered, which is:

where $\left\{{\epsilon }_0\right\}$ represents strain vector at any point of the free damping layer.

3.1. The relationship between energy loss of the damping material on each element and the displacement of the nodes of the curved plate (shell) structure

The purpose of damping materials is to convert kinetic energy into heat energy to reduce the vibration of the thin plate. The way to determine the location where the damping material pasted on is to find the location where damping material’s energy will lose more.

Energy loss of damping material on each element in a vibration cycle is $W^e={\int }_V{W}_{d2}\left(T\right)dv$. Then $W^e$ can be expressed as $W^e=\alpha {\int }_V{\left\{{\epsilon }_0\right\}}^T\left[D_2\right]\left\{{\epsilon }_0\right\}dv$, which also can be expressed by the node displacement of the base metal plate as below (Eq. (18)):

18

$W^e={\int }_V{W}_{d2}\left(T\right)dv=\alpha {\int }_V{\left\{{\epsilon }_0\right\}}^T\left[D_2\right]\left\{{\epsilon }_0\right\}dv$
$=\alpha {\int }_V{\left(\left[B_2^{\left(m\right)}\right]\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}+z\left[B_2^{\left(b\right)}\right]\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}\right)}^T\left[D_2\right]\left(\left[B_2^{\left(m\right)}\right]\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}+z\left[B_2^{\left(b\right)}\right]\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}\right)dv$
$=\alpha \left\{{\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}}^T{\int }_V{\left[B_2^{\left(m\right)}\right]}^T\left[D_2\right]\left[B_2^{\left(m\right)}\right]dv\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}+2{\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}}^{T}z{\int }_V{\left[B_2^{\left(m\right)}\right]}^T\left[D_2\right]\left[B_2^{\left(m\right)}\right]dv\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}\right.$
$\left.+{\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}}^T{\int }_V{z}^2{\left[B_2^{\left(b\right)}\right]}^T\left[D_2\right]\left[B_2^{\left(b\right)}\right]dv\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}\right\}$
$=\alpha \left\{h_2{\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}}^T\left[K^{\text{'}}\right]\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}+\left({\left(\frac{h_1}{2}+h_2\right)}^2-{\left(\frac{h_1}{2}\right)}^2\right){\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}}^T\left[K^{″}\right]\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}\right.$
$\left.+\frac{1}{3}\left({\left(\frac{h_1}{2}+h_2\right)}^3-{\left(\frac{h_1}{2}\right)}^3\right){\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}}^T\left[K^{‴}\right]\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}\right\},$

where:

19

$\begin{array}{c}\left[K^{\text{'}}\right]={\int }_{-l_2}^{l_2}{\int }_{-l_1}^{l_1}{\left[B_2^{\left(m\right)}\right]}^T\left[D_2\right]\left[B_2^{\left(m\right)}\right]dxdy,\left[K^{″}\right]={\int }_{-l_2}^{l_2}{\int }_{-l_1}^{l_1}{\left[B_2^{\left(m\right)}\right]}^T\left[D_2\right]\left[B_2^{\left(b\right)}\right]dxdy,\end{array}$
$\left[K^{‴}\right]={\int }_{-l_2}^{l_2}{\int }_{-l_1}^{l_1}{\left[B_2^{\left(b\right)}\right]}^T\left[D_2\right]\left[B_2^{\left(b\right)}\right]dxdy,$

where $\left[K^{\mathrm{\text{'}}}\right]$, $\left[K^{″}\right]$ and $\left[K^{‴}\right]$ are membrane stiffness matrix, coupling stiffness matrix and bending stiffness matrix of the four nodes rectangular plate element respectively. Because the thickness of the shell and the damping layer are constants, the coefficients in Eq. (18) are also constants and independent to coordinate. Given:

20

$c_1=h_2,c_2={\left(\frac{h_1}{2}+h_2\right)}^2-{\left(\frac{h_1}{2}\right)}^2,c_3={\left(\frac{h_1}{2}+h_2\right)}^3-{\left(\frac{h_1}{2}\right)}^3.$

Fig. 2Sketch of the shell with damping material layer

The Eq. (20) above can be simplified as:

21

$W^e=\alpha \left\{c1{\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}}^T\left[K^{\text{'}}\right]\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}+c2{\left\{\begin{array}{c}{u}^e\\ v^e\end{array}\right\}}^T\left[K^{″}\right]\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}+c3{\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}}^T\left[K^{‴}\right]\left\{\begin{array}{c}{w}^e\\ {\theta }_{xi}\\ {\theta }_{yi}\end{array}\right\}\right\}.$

According to the aimed order vibration mode of the metal plate, energy loss of damping materials on each element can be calculated by Eq. (21). Damping materials will be pasted on the element location where damping material energy will lose most, and then the second gradually, until the optimization target is achieved.

4. Process of the fast topology optimization

From the view of energy, damping means energy attenuation. According to Eq. (21) the relationship between energy loss of the damping materials on each element and the displacement of each node in a vibration cycle, a fast topology optimization method for damping materials laid on elastic curved plate (shell) structure was established. Damping materials were pasted on the most effective location, which is the object of the damping topological optimization. Only one eigenvalue needs to be computed. And it is unnecessary to solve a large complex differential equation or matrix eigenvalue.

The optimization process is described as below:

1) Complex structures can be established by commercial finite element software. Matlab subroutines were produced to read out the finite element and node information. And also stiffness matrix, mass matrix, and the corresponding modal vibration mode were calculated.

2) It is few modals that affect the vibration, aimed at which vibration or noise control can be more effective. According to modal acoustic transfer vector or structural modal participation factor, the modal orders which have more influence on the vibration or noise reduction could be found.

3) One order modal can be optimized or make use of weighted factor several order modals can be optimized. According to the aimed order vibration mode of the metal plate, energy loss of damping materials on each element can be calculated by Eq. (21).

4) Supposing the optimized modal is $i$th. Energy loss of damping material on each element in one vibration cycle was calculated. Paste damping materials on the location where energy loss the most, and then the second most. The rest can be done in the same manner, until achieve the optimization target. At the same time filter formula used effectively inhibit the checkerboard phenomenon.

5) Contrast the intensity of sound pressure of a specified point in the acoustic cavity before and after the optimization respectively, the validity of this method was verified.

Flowchart of the optimization process of pasting damping layer to elastic shell for vibration noise reduction is show in Fig. 3.

The method in this paper is quite different from evolutionary optimization techniques. Evolutionary optimization method requires multiple iterations and a small amount of elements are removed in each iteration. However the method in this paper is called fast topology optimization algorithm which only needs to compute one eignvalue of the metal plate. And also this method can be considered as a kind of approximate algorithm, for using Eq. (21) to calculate the energy loss is based on the vibration mode without pasting damping materials. Assuming that pasting a small amount of damping material has no effect on structural vibration mode, yet, there was always a little bit influence. For large structures, the influence of vibration mode with a small amount of damping materials pasted on is really small.

5. Example

Fig. 4 shows a curved plate and an acoustic cavity structure. Force was exerted on the curved plate. Acoustic radiation was produced mainly because of the forced plate. Damping materials were pasted on the surface of the forced plate. The topology optimization procedure is implemented in MATLAB, and the flowchart is given in Fig. 3.

Fig. 3Flowchart of the optimization process

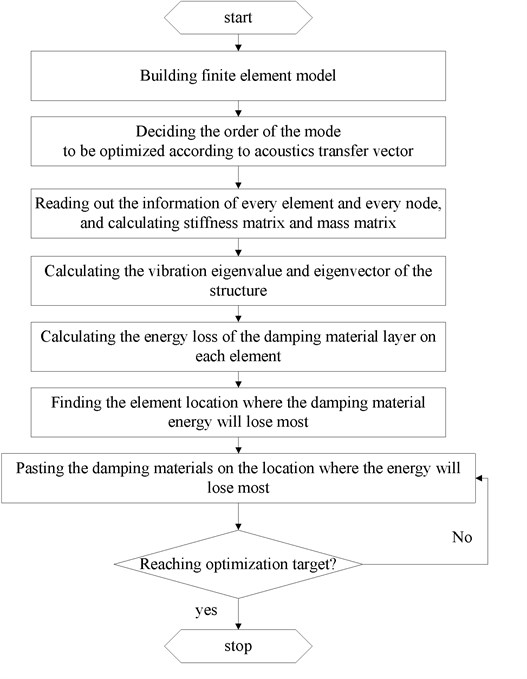
Fig. 4Sketch of curved plate – cavity structure

The length-width-height of the curved plate-cavity structure respectively is 1.2 m×0.6 m×1.0 m. Material parameters of metal layer and damping material layer are presented in Table 1.

First of all, finite element model of the curved plate-acoustic structure was built by the finite element software. Curved plate model is shown as Fig. 5.

Fig. 5Node distribution on the curved plate

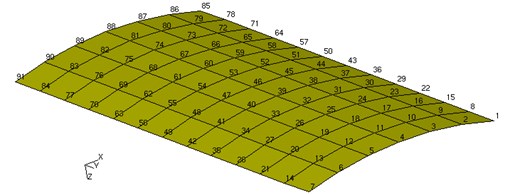
The elastic curved plate-cavity structure can be simulated for a driving cab. Sound pressure at the point of person’s ear was considered. The information of elements and nodes were read out, frequency and vibration mode were calculated by Matlab subroutines. Commercial sound simulation software was used to determine the order of the plate to be optimized.

Fig. 6Node distribution and the specified node (85) in the cavity

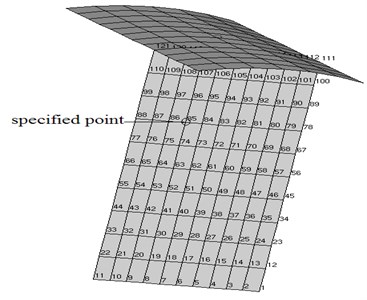
For specified point as shown in Fig. 6, the order of the mode affect the level of the sound pressure most is different. According to modal acoustic transfer vector, the plate (shell) mode which affects the sound pressure of the specified point most was found. Fig. 7 shows transfer function between structural modal and point in the cavity.

From the Fig. 7 above, we get that the third order modal of the plate has the largest influence on the sound pressure of the specified point 85. So aimed at the third modal, using the method described in this paper, and according to the flowchart of the optimization process Fig. 4, the result of the damping layer sticking position diagram is shown in Fig. 9. Setting the finial damping layer occupy half of the whole area. The optimization process can be sketched as: 1) Building finite element model take advantage of commercial finite element software; 2) Writing MATLAB programme, reading out the information of every element and every node, and calculating stiffness matrix and mass matrix; 3) Calculating the vibration eigenvalue and eigenvector of the curved-plate; 4) Calculating the energy loss of the damping material layer on each element according to Eq. (21); 5) Pasting the damping materials on the location where the energy will lose most until reaching optimization target.

Sound pressure level at specified point was calculated taking advantage of commercial sound simulation software. Two models were established for curved-plate without damping layer and with damping layer respectively. And these two modes were meshed in finite element software. Exerting force to the structure model, displacement response of each node was calculated and saved, which would be imported to sound simulation software. According to these displacement response of each node, sound pressure level at specified point was calculated, which was shown as Fig. 9. Two pictures represent two cases the curved plate with damping materials and without damping materials respectively. The figures show that in the low frequency area sound pressure is decreased obviously.

Fig. 7Modal acoustic transfer vector to specified point 85 in the sound radiation field

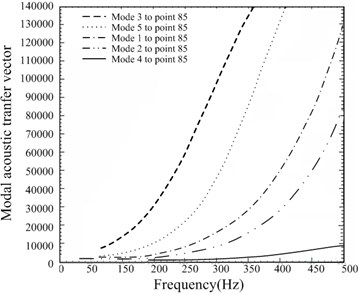
Fig. 8Location of the damping material after optimization

Fig. 9Sound pressure level at the specified point

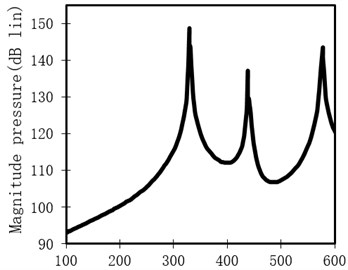
a) Before optimization

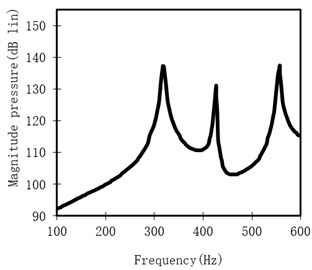
b) After optimization

6. Conclusions

In this paper, a fast topology optimization method of damping material layer for noise reduction to elastic curved plate-cavity structure was given. Only calculating one eigenvalue can get approximate optimal distribution of damping material layer, so the topology optimization method is a kind of approximate and fast method.

The purpose of the topological optimization is to use less as far as possible the damping materials to reach the best result of vibration or noise reduction effect. Finite element model was established by commercial software which is easy for complex structure. Write Matlab subroutines to read out nodes and elements information of the model, calculate the stiffness matrix, mass matrix, and the corresponding modal vibration mode. According to modal acoustic transfer vector or structural modal participation factor, the order of the mode to be optimized was decided. Aimed at the order to be optimized, energy loss of damping material on each element in a period was obtained. Paste damping material on the location where the damping material energy would lose most, and the second most gradually, until optimization target was achieved. Numerical example results show that this method is simple, suitable for engineering application.