Analytical impact of the sliding friction on mesh stiffness of spur gear drives based on Ishikawa model

Li, Zhengminqing; Chen, Hongshang; Chen, Jiansong; Zhu, Rupeng

Vibroengineering Procedia

Browse Procedia

Published: 03 November 2014

Check for updates

Analytical impact of the sliding friction on mesh stiffness of spur gear drives based on Ishikawa model

Zhengminqing Li¹

Hongshang Chen²

Jiansong Chen³

Rupeng Zhu⁴

^{1, 2, 4}Nanjing University of Aeronautics and Astronautics, Nanjing, China

³Southeast University, Nanjing, China

Corresponding Author:

Zhengminqing Li

Cite the article Download PDF

Downloads 1344

Abstract

Mesh stiffness always is a studying focus of gear dynamics. In the issue, a solution for the calculation of mesh stiffness considering the sliding friction effect is constructed, and the influence of the sliding friction on mesh stiffness is analyzed. Further, the analytical results indicate mesh stiffness is sensitive to the sliding friction in poorly lubricating conditions specially. These contributions would not only simplify the calculation of mesh stiffness associated with the sliding friction but also be good for assessing the dynamic behaviors of spur gear drives in some special operating conditions

1. Introduction

Mesh stiffness always is one of studying focuses of gear dynamics since it is important for inherent properties and dynamic response of gear drives. There are many literatures discussing mesh stiffness over the past several years. In these issues [1-8], the researchers constructed analytical solutions of mesh stiffness such as Ishikawa method. However, how the sliding friction affects mesh stiffness is yet to be resolved or addressed by the gear dynamics researchers. Thus, in this study, an incremental angle of action caused by the sliding friction is included into Ishikawa model for the calculation of mesh stiffness considering the sliding friction effect as well as the impact of the sliding friction on mesh stiffness is analyzed. Furthermore, the analytical results indicate that mesh stiffness of spur gear drives is sensitive to the sliding friction in poor lubrication conditions specially. These contributions would be helpful for assessing mesh stiffness associated with the sliding friction.

2. The incremental angle of action caused by the sliding friction

2.1. The sliding friction direction on the tooth

The relative velocity on the tooth flank, only at the pitch point, is equal to zero during the meshing process of spur gear drives. Therefore, the sliding friction direction on the tooth of the driving gear is apart from the pitch point. In contrast, that on the tooth of the driven gear is pointing to the pitch point. The sliding friction direction on the tooth of a gear pair is given in Fig. 1.

Fig. 1The sliding friction directions on the tooth of a gear pair

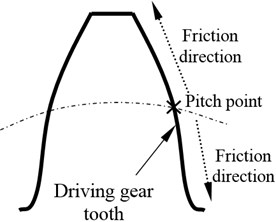
a) On the driving gear tooth

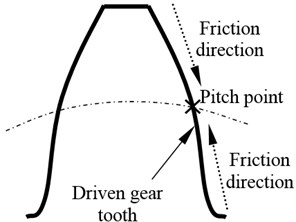
b) On the driven gear tooth

2.2. The pressure distribution on the tooth

The contact ratio is important for describing the pressure distribution on the tooth. The relationship between the contact ratio ε and the deformation of the tooth during the meshing process is shown in Fig. 2.

In Fig. 2, A, B, C, D and E are the mesh points, $p_{b}$ is the pitch of the base circle, $q$ is the flexibility of the tooth at any mesh points, which can be expressed as [8, 9]:

1

q = q_{B r 1} + q_{B r 2} + q_{B t 1} + q_{B t 2} + q_{G 1} + q_{G 2} + q_{s 1} + q_{s 2} + q_{h 12},

where the subscript 1 and 2 represent the pinion and the gear respectively. Meanwhile, the equations of the variables in Eq. (1) are listed in Table 1.

Table 1The equations of the variables in Eq. (1)

Value name	Equations [8, 9]
$q_{B r}$	$\frac{12 {c o s}^{2} (ω_{x})}{E s_{f}^{3}} (h_{x}^{2} h_{r} - h_{x} h_{r}^{2} + \frac{h_{r}^{3}}{3})$
$q_{B t}$	$\frac{6 {c o s}^{2} (ω_{x})}{E s_{f}^{3}} {(h_{i} - h_{r})}^{3} [\frac{h_{i} - h_{x}}{h_{i} - h_{r}} (4 - \frac{h_{i} - h_{x}}{h_{i} - h_{r}}) - 2 l n (\frac{h_{i} - h_{x}}{h_{i} - h_{r}}) - 3]$
$q_{G}$	$\frac{24 h_{x}^{2} {c o s}^{2} (ω_{x})}{π E s_{f}^{2}}$
$q_{s}$	$\frac{2 (1 + γ) {c o s}^{2} (ω_{x})}{E s_{f}} [h_{r} + (h_{i} - h_{r}) l n (\frac{h_{i} - h_{r}}{h_{i} - h_{r}})]$
$q_{h 12}$	$\frac{2 (\frac{1 - γ_{1}^{2}}{E_{1}} + \frac{1 - γ_{2}^{2}}{E_{2}})}{π}$

In Table 1, $E$ is the elastic modulus, $γ$ is the Poisson ratio, $s_{f}$ is the root thickness, $h_{i}$ , $h_{x}$ and $h_{r}$ are the geometric parameters of gears and $ω_{x}$ is the angle of action.

According to the tooth deformation, as shown in Fig. 2, the pressure at the mesh points as A, B, C, D and E, can be derived in a piecewise form as:

2

f_{N} = \{\begin{array}{l} \frac{q_{A}}{q_{A} + q_{D}} (\frac{9550 P c o s (α)}{N r}), & A, \\ \frac{q_{B}}{q_{B} + q_{E}} (\frac{9550 P c o s (α)}{N r}), & B, \\ (\frac{9550 P c o s (α)}{N r}), & C, \\ \frac{q_{D}}{q_{A} + q_{D}} (\frac{9550 P c o s (α)}{N r}), & D, \\ \frac{q_{E}}{q_{B} + q_{E}} (\frac{9550 P c o s (α)}{N r}), & E, \end{array}

where $P$ is the power, $N$ is the input pinion speed, $r$ is the radius of the reference circle of the pinion and $α$ is the pressure angle of the reference circle of the driving gear.

2.3. The solution constructed

The solution for the calculation of mesh stiffness associated with sliding friction, namely Ishikawa model considering the sliding friction effect, is constructed and shown in Fig. 3.

Fig. 2The relationship between the contact ratio and the deformation of the tooth

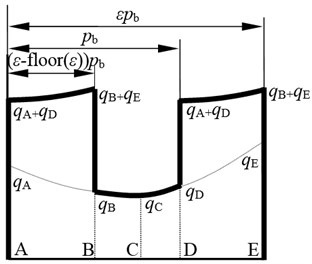
Fig. 3Ishikawa model considering the sliding friction

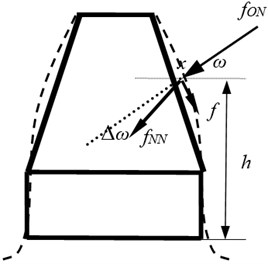
As given in Fig. 3, the change, comparing the proposed model with Ishikawa model [8, 9], is essentially the incremental angle of action $Δ ω$ caused by the sliding friction. Therefore, considering both the sliding friction direction as shown in Fig. 1 and the pressure distribution on the tooth described as Eq. (2), the incremental angle of action $Δ ω$ can be deduced as:

3

Δ ω = \{\begin{array}{l} a t a n (λ \frac{q_{A}}{q_{A} + q_{D}}), & A, \\ a t a n (λ \frac{q_{B}}{q_{B} + q_{E}}), & B, \\ 0, & C, \\ - a t a n (λ \frac{q_{D}}{q_{A} + q_{D}}), & D, \\ - a t a n (λ \frac{q_{E}}{q_{B} + q_{E}}), & E . \end{array}

3. Simulation and analysis

Several different sliding friction coefficients and the basically geometric parameters of an example case, which are from the reference [1], are listed in Table 2.

Table 2The simulation parameters

Basic geometric parameters		Driving gear	Driven gear	Unit		Description
	$m$	8		mm		Module
	$α$	20		deg		Pressure angle
	$z$	95	22	–		Number of tooth
Friction coefficient	Condition 1		Condition 2		Condition 3
	0.05		0.3		0.64

Table 3The average mesh stiffness

	Ref. [1]	Without the friction	Condition 1	Condition 2	Condition 3	Unit
Average mesh stiffness	25	23.2099	23.2607	23.9779	26.3876	N/μm mm

The incremental angle of action of the pinion and that of the driven gear are simulated and shown in Fig. 4. Moreover, the time-varying mesh stiffness considering the sliding friction effect is given in Fig. 5 and the results of the average mesh stiffness are listed in Table 3.

The calculating error of the average mesh stiffness based on between the proposed model and Ishikawa model, and the difference of the average mesh stiffness between without and with the sliding friction effect can be reduced to one equation, which can be defined as:

4

η = \frac{| K - K_{B} |}{K_{B}} \times 100 %,

where $K$ is the average mesh stiffness without the sliding friction based on the proposed model and $k_{B}$ is the benchmark from the reference [1] or $K$ is the average mesh stiffness with the sliding friction and $k_{B}$ is that without the sliding friction and based on the proposed model. The calculating error of the example case is 7 %, which is acceptable. Moreover, the differences of the average mesh stiffness between without and with the sliding friction effect are listed in Table 4.

Fig. 4The incremental angle of action

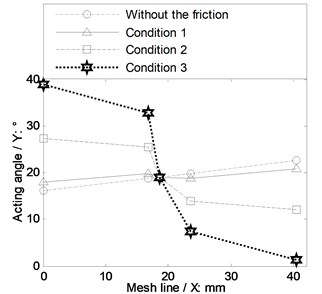
a) On the driving gear

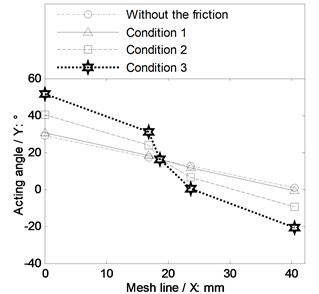
b) On the driven gear

Fig. 5The time-varying mesh stiffness considering the sliding friction effect

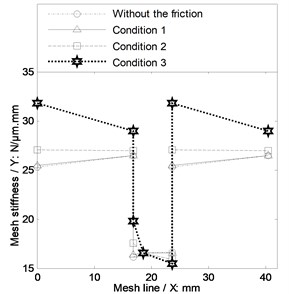
The results in Table 4 indicate the average mesh stiffness of spur gear drives is sensitive to the sliding friction in poor lubrication conditions specially. Moreover, in the case of Fig. 4 and Fig. 5, the angle of action would be increased in the engagement, and not be changed at the pitch point and be decreased at the meshing-out point due to the sliding friction. Furthermore, the trend of the time-varying mesh stiffness of spur gear drives would be changed.

Table 4The differences of the average mesh stiffness between without and with the sliding friction effect

	Condition 1	Condition 2	Condition 3
The difference	0.2 %	3.31 %	13.69 %

4. Conclusions

In the study, two important works can be extracted as follows:

1) The incremental angle of action caused by the sliding friction is joined into Ishikawa model to construct a solution for the calculation of mesh stiffness considering the sliding friction effect of spur gear drives.

2) The impact of the sliding friction on mesh stiffness of spur gear drives is analyzed and the results indicate mesh stiffness is sensitive to the sliding friction in poorly lubricating conditions specially.

These conclusions would be benefit to assess mesh stiffness associate with the sliding friction and help to analyze the dynamic behaviors of spur gear drives in some special operating conditions.

References

Pedersen R., Santos I. F., Hede I. A. Advantages and drawbacks of applying periodic time-variant modal analysis to spur gear dynamics. Mechanical Systems and Signal Processing, Vol. 24, Issue 5, 2010, p. 1495-1508.

Search CrossRef
Xihui Liang, Ming J. Zuo, Tejas H. Patel Evaluating the time-varying mesh stiffness of a planetary gear set using the potential energy method. Journal of Mechanical Engineering Science, 2013, p. 1-13.

Search CrossRef
Li S., KahramanA. A spur gear mesh interface damping model based on elastohydrodynamic contact behavior. International Journal of Powertrains, Vol. 1, Issue 1, 2011, p. 4-21.

Search CrossRef
Li S., Kahraman A. A tribo-d ynamic model of a spur gear pair. Journal of Sound and Vibration, Vol. 332, 2013, p. 4963-4978.

Search CrossRef
Song He, Todd Rook, Rajendra Singh Construction of semianalytical solutions to spur gear dynamics given periodic mesh stiffness and sliding friction functions. Journal of Mechanical Design, Vol. 130, 2008, p. 1-9.

Search CrossRef
Gang Liu, Robert G. Parker Impact of tooth friction and its bending effect on gear dynamics. Journal of Sound and Vibration, Vol. 320, 2009, p. 1039-1063.

Search CrossRef
Lassâad Walha, Tahar Fakhfakh and Mohamed Haddar Nonlinear dynamics of a two-stage gear system with mesh stiffness fluctuation, bearing flexibility and backlash. Mechanism and Machine Theory, Vol. 44, 2009, p. 1058-1069.

Search CrossRef
Shi J. L., Ma X. G., Xu C. L., Zang S. J. Meshing stiffness analysis of gear using the ishikawa method. Applied Mechanics and Materials, Vol. 401, 2013, p. 203-206.

Search CrossRef
Zhu X., et al. Analysis of Load Capacity of Gears. Beijing, Higher Education Press, 1992.

Search CrossRef

About this article

Received

Accepted

10 July 2014

Published

03 November 2014

Keywords

the sliding friction

mesh stiffness

spur gear drives

Ishikawa model

Acknowledgements

The authors are grateful for the financial support provided by NSFC under No. 51105194 and No. 51375226 as well as CSC under contract No. 201206835011.

In addition, the authors declare that there is no conflict of interests regarding the publication of this article.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.