Application of maximum correlated Kurtosis deconvolution on bearing fault detection and degradation analysis

1. Introduction

Rotating parts are very important for many mechanical systems. Their failures will lead to great production loss and maintenance costs. Take wind turbine for example, the crane cost for replacing the gearbox is more than 60,000 $. Meanwhile, if the failures occur in seasons with good wind, there will be a great of wind power lost. For the gearbox replacement of wind turbine, 50 % are due to the high speed bearing faults. Therefore, bearing faults detection and degradation analysis are very important.

Fault detection, diagnosis and prognosis are the main research contents of many academic groups these years. Fault diagnosis has two meanings. One is to diagnose the bearing fault level, the other is to distinguish bearing fault from other components like gear and shaft. This is very important for maintainers to know what spare part should be prepared. However, we do not know when to replace the fault bearing? So, the remaining useful life (RUL) prediction is researched to address this problem. As we know, for the bearing degradation, the health indexes are always flat at the early period. The RUL prediction is effect only when the indexes start progress. This point is called the change point. This point denotes the bearing start to enter into a degradation process. So, this change point detection is very important for RUL prediction and maintenance actions. Earlier the change point detected, more lead time remained. This will increase the bearings’ availability.

Take wind turbine maintenance contract as example, many farmers select the performance based contract (PBC) but not the material based contract. In the PBC, availability is the index related to the maintenance fee what farmers will pay. So, the earlier fault detection ability is very important because it can improve the availability and save much money for wind farmers. For bearing’s incipient fault, the impulsive signals produced by the fault are always immersed in the great background noise. So, we need to find some methods which can extract or enhance the impulsive signal enabling the fault easily been found.

There are two methods to realize this goal. One is to find the optimum frequency band which has the most impulsive signals. The other is to enhance the impulsive signal directly which can enable the fault detection easier. Antoni [1] proposed the formalization of the spectral kurtosis (SK) by means of the Wold-Cramér decomposition of “conditionally non-stationary” processes. Later, Antoni and Randall [2] used SK in the condition monitoring of rotating machines. SK can provides a robust way of detecting incipient faults even in the presence of strong masking noise. Besides, it can offers an almost unique way of designing optimal filters for filtering out the mechanical signature of faults. Meanwhile, the Kurtogram was proposed. Sawalhi et al. [3] combined the minimum entropy deconvolution (MED) with the SK to enhance the fault detection ability. The results show that the MED technique can sharpens the impulse signals produced by bearing or gear fault. It is demonstrated can increase the kurtosis value and reflect the fault severity appropriately. Zhang and Randall [4] proposed using genetic algorithms combined with fast kurtogram to optimize the filter centre frequency and bandwidth. Wang and Liang [5] proposed an adaptive SK technique for the fault detection of rolling element bearings. It is implemented through right-expand a given window along the frequency axis by merging it with its subsequent neighboring windows. Traditionally, the Kurtogram is based on the short time Fourier transform or FIR filters. However, this will lead to the limited accuracy improvement of Kurtogram method for extracting the transient characteristics from a noisy signal. Therefore, Lei et al. [6] introduced wavelet packet transform into the Kurtogram which can overcome the shortcomings of original Kurtogram. Eftekharnejad et al. [7] tried to apply Acoustic Emission technology for machine health monitoring and compared the effectiveness of applying the Kurtogram to both vibration and AE data from a defective bearing. Guo et al [8] developed a hybrid signal processing method that combines SK with ensemble empirical mode decomposition (EEMD). SK can find the optimal band-pass filter which can extract impulsive signals from very noise case. This is benefit for the diagnosis ability of EEMD. Wang et al [9] developed an enhanced kurtogram method for bearing fault diagnosis. The kurtosis values are calculated based on the power spectrum of the envelope of the signals extracted from wavelet packet nodes at different depths. Chen et al [10] developed an improved version of fast Kurtogram named as “fast spatial-spectral ensemble kurtosis Kurtogram”. In this technique, discrete quasi-analytic wavelet tight frame (QAWTF) expansion methods are incorporated as the detection filters. The QAWTF is constructed based on the dual tree complex wavelet transform. It possesses better vibration transient signature extracting ability and enhanced time-frequency localizability compared with conventional wavelet packet transforms.

Above mentioned methods related to the SK are all used to find the optimum centre frequency and bandwidth except the MED technique. However, this is based on the precondition that the bearing has faults. Usually, there are no faults existing at the beginning operation of bearings. So, using these techniques to find the optimal centre frequency and bandwidth is difficult. However, MED [11] technique can directly enhance the impulsive signal which enables the fault detection easier. But, there is a limitation for MED that it will prefer to deconvolve only a single impulse or a selection of impulses, as opposed to the desired periodic impulses repeating at the period of the fault. Based on MED technique, McDonald et al. [12] proposed an improved novel deconvolution norm, Correlated Kurtosis (CK). It takes advantage of the periodicity of the faults. So, a new deconvolution method named, maximum correlated Kurtosis deconvolution (MCKD), is proposed to select a FIR filter to maximize the CK of the resulting signal which emphasizes the high Kurtosis while encouraging periodicity about a specific period. Finally, they used gear tooth chip experiment to validate their methods and look forward to use this method to do the bearing fault diagnosis. This method is very robust to do the incipient fault detection of rotating machineries. It is no need to know something in advance except the fault frequencies which can be know through the geometric structure of bearing. It can enhance the periodic impulsive signal produced by bearing fault. Then, the envelope analysis can be used to locate the fault.

The main goal of this paper is to validate the effectiveness of MCKD on bearing fault detection. The rest of this paper is organized as follows. The MCKD method is introduced briefly in Section 2. The data analysis of bearing fault experiment and bearing degradation experiment using MCKD is described in Section 3. Section 4 concludes the work.

2. Maximum correlated Kurtosis deconvolution

In MED, the filtering goal is to maximize the Kurtosis with assumed zero-mean:

However, maximizing the Kurtosis also has drawback that it prefers to find the big impulse which cannot denotes the periodic impulse produced by bearing or gear fault. In others words, a single pulse which indeed is a noise may has higher Kurtosis than the periodic impulse of the fault. So, in order to solve this problem, CK is proposed as follows:

These two new norms can filter output a periodic impulse which has high Kurtosis. $N$ is the number of samples in the input signal $x$, $L$ is the length of FIR filter and the $T$ is the period related to the fault frequency of interest. The detail information of filtering process can be found in [12].

3. Two bearing experiments and data analysis

3.1. Experiment 1 and results

The test rig [13] was equipped with a NICE bearing with the following parameters: roller diameter 0.235 inch, pitch diameter 1.245 inch, number of elements is 8, and the contact angle equal to 0°. The input shaft rotation rate is 25 Hz. The sample frequency is 48,828 Hz and lasting 3 seconds. For outer race fault conditions, seven data sets are acquired respectively under load 25, 50, 100, 150, 200, 250, 300 lbs. Through the geometric parameters of NICE bearing, the fault characteristic frequencies can be calculated as illustrated in Table 1. And we define the four fault characteristic frequencies as ball pass frequency inner race (BPFI), ball pass frequency outer race (BPFO), ball spin frequency (BSF), and fundamental train frequency (FTF). The outer race fault is depicted in Fig. 1.

Table 1Fault characteristic frequencies at the input frequency of 25 Hz

Type of faults	Fault characteristic frequencies (Hz)
Outer race fault	81.12
Inner race fault	118.88
Ball fault	63.86
Cage fault	10.14

Fig. 1Outer race fault

For this experiment, we can use MCKD to enhance the impulsive signal produced by outer race fault of load 25 lbs. In this case, the filter size is selected as 100, $M$ is selected as 2, and iteration time is selected as 100. The time domain signals before and after MCKD processing can be illustrated in Fig. 2(a) and (b).

Fig. 2a) Time domain signal before MCKD processing; b) Time domain signal after MCKD processing

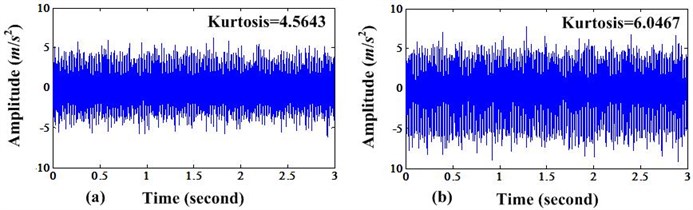
From these two figures, we can see that the amplitudes of impulsive signals have been enlarged and the signals after MCKD processing have higher Kurtosis value than before. The spectrum of FFT before and after MCKD processing can be depicted in Fig. 3(a) and (b).

Fig. 3a) FFT spectrum before MCKD processing; b) FFT spectrum after MCKD processing

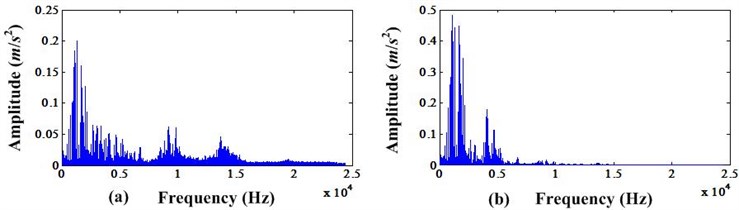
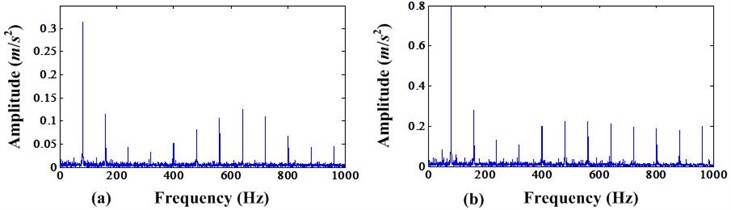
Fig. 4a) Envelope spectrum before MCKD processing; b) Envelope spectrum after MCKD processing

From Fig. 3, we can see that the amplitude of resonance domain after MCKD processing is higher than the amplitude before. In addition, we can compare the FFT spectrum of envelope signals of these two cases. It can be depicted in Fig. 4.

From Fig. 4, we can see that the amplitudes of envelope spectrum after MCKD processing are higher than the envelope spectrum before MCKD processing. In addition, the iteration number vs CK value in this MCKD process can be shown in Fig. 5. It is found that the CK value achieve a big value when the iteration number is bigger than 40 and has minor variation for each iteration. So, we can select 40 as the iteration number for saving calculation time.

From above results shown in Figs. 2-4, we can conclude that the MCKD can enhance the periodic impulse signal produced by bearing fault. And this will make the fault easier detection especially for the incipient fault.

Because the limited pages, the results of all the data sets can be concluded in the Table 2. From this table, it can be concluded that MCKD method is very effective for enhancing the bearing fault detection ability.

Table 2Kurtosis and envelope amplitude value comparison

Item	25 lbs	50 lbs	100 lbs	150 lbs	200 lbs	250 lbs	300 lbs
Kurtosis before MCKD	4.56	5.09	4.39	4.04	11.89	6.59	17.68
Kurtosis after MCKD	6.05	8.55	5.98	8.37	24.78	18.48	62.78
Evelope amplitude at 81 Hz before MCKD	0.32	0.27	0.21	0.26	0.48	0.33	1.12
Envelope amplitude at 81 Hz after MCKD	0.79	0.58	0.48	0.31	0.59	0.51	0.89

3.2. Experiment 2 and results

This bearing test rig hosts four bearings on one shaft. The shaft is driven by an AC motor. The rotation speed was kept constant at 2000 rpm. The load added to the shaft is 6000 lbs by a spring mechanism. There was a magnetic plug installed in the oil feedback pipe which used to collect debris from the oil as the evidence of bearing degradation. The test will stop when the accumulated debris adhered to the magnetic plug exceeds a certain level and causes an electrical switch to close. Four Rexnord ZA-2115 double row bearings were installed on one shaft. The bearings have 16 rollers in each row. The pitch diameter is 71.501 mm. The roller diameter is 8.4074 mm and the tapered contact angle is 15.17°. On each bearing, two PCB 353B33 High Sensitivity Quartz ICP Accelerometers were installed for a total of 8 accelerometers (one vertical $Y$ and one horizontal $X$ on each). Vibration data was collected every 20 minutes by a National Instruments DAQCard-6062E data acquisition card. The data sampling rate is 20 kHz and the data length is 20,480 points. Each data file consists of 8 columns. Each column corresponds to one accelerometer signal.

Fig. 5CK value variations with the iteration number under the filtering process

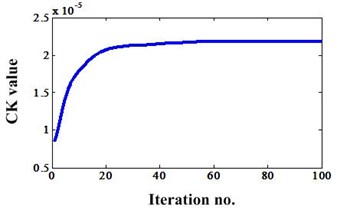
Fig. 6The RMS value of bearing 4

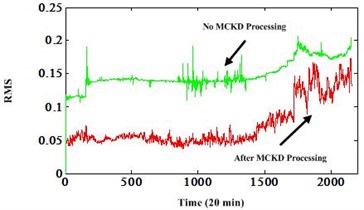
In order to demonstrate the effectiveness of MCKD method, these degradation data sets are used to analyze. The Fig. 6 is the root mean square (RMS) value comparison between two different processing methods. One is no MCKD processing, the other is with MCKD processing. All these degradation indexes are post-processed by autoregressive filtering to remove the noise. We can see that the RMS extracted from the MCKD processed signals has good degradation trend than the RMS extracted from the original signals directly. And the change point is earlier than before. This is very beneficial for the RUL prediction and can provide more lead time for the logistic actions.

4. Conclusions

This paper further demonstrates the effectiveness of MCKD on bearing fault analysis. It contains two parts. One is the bearing fault detection ability enhancement. The other is the enhanced bearing incipient fault detection and degradation analysis. The first is very meaningful when the bearing fault signal immersed in the great noise. It can enable the envelope analysis etc methods more effective. The second can benefit the RUL prediction and the logistic actions due to its earlier change point detection and good trend degradation indicator extraction ability. In future, we can combine MCKD with other methods to realize the automotive fault analysis.